大学化学笔记

本文最后更新于：2023年10月7日 上午

第一章 化学热力学基础

  • 热力学体系
    • 敞开体系
    • 封闭体系
    • 孤立体系
  • 状态函数
    • 度量性质
    • 强度性质

  • 状态函数的特点：
    1.体系的状态一定，其状态函数都有确定值
    2.状态函数的改变量只取决于体系的始态和终态，与变化的具体途径无关
    3.在同一状态下，不同类型的状态函数的任意组合或运算仍为体系的状态函数；但在不同状态下，同一状态函数的组合不能表示为新的状态函数
    4.若体系从某一始态出发，最终回到原始状态，则所有的状态函数都恢复至原有数值，即状态函数经历一个循环变化后，各状态函数的变化值都为零，此变化过程称为循环过程

  • 热力学过程：

    • 恒温过程
    • 恒压过程
    • 恒容过程
    • 绝热过程

  • 一些符号的定义：

    • Q：热是指因温度不同而在体系与环境之间传递的能量，用符号Q表示
    • U：热力学将体系内的一切能量的总和称为体系的热力学能，也称内能，用符号U表示，单位为KJ
    • W：除热以外，体系与环境之间传递的一切能量称为功，用符号W表示
      • $W_\text{体}$：当体系仅因体积的膨胀或压缩而与环境之间产生的能量传递称为体积功
      • $W_\text{非}$：除体积功以外所有形式的功称为非体积功

  • 热力学第一定律：$\Delta \mathrm{U}=\mathrm{Q}+\mathrm{W}$

  • 理想气体：$pV=nRT$
    • R为理想气体常数=$\mathrm{R}=8.314 \mathrm{~J} / \mathrm{mol}/\mathrm{K}$
    • 理想气体内能U只与T有关
    • 分压定律
  • 理想气体的恒温膨胀
    • 一次膨胀：$W_1=-p_2(V_2-V_1)$
    • 无限次膨胀：$W=nRT\ln{\frac{V_2}{V_1}}$
  • 反应热
    • 恒容：$Q_v=\Delta \mathrm{U}$
    • 恒压：$\mathrm{Q}_{\mathrm{p}}=\Delta \mathrm{H}=\Delta \mathrm{U}+\Delta \mathrm{PV}=\Delta \mathrm{U}+\Delta \mathrm{nRT}$
  • 盖斯定律
  • 一些标准焓
    • 标准态对温度没有规定，要标出温度
    • 气体物质的标准状态指在分压为$100kPa(p^{\theta})$、具有理想气体行为的纯气体
    • 固体和液体的标准状态分别为$p^{\theta}$下的纯固体和纯液体
    • 溶液中的溶质A，其标准状态为$p^{\theta}$下质量摩尔浓度$m_A=1mol \cdot kg^{-1}$，水溶液中通常近似为$c_A=1mol\cdot dm^{-3}$
    • 反应焓变$\Delta_{\mathrm{r}} \mathrm{H}_{\mathrm{m}}^{\theta}(\mathrm{T})$ （=生成焓的生成物-反应物；或者燃烧焓的反应物-生成物）
    • 标准生成焓$\Delta_{\mathrm{f}} \mathrm{H}_{\mathrm{m}}^{\theta}(\mathrm{T})$
    • 燃烧焓$\Delta_{\mathrm{c}} \mathrm{H}_{\mathrm{m}}^{\theta}(\mathrm{T})$

第二章 化学反应的基本原理

  • 自发过程：
  • 一切自发过程的逆过程都是非自发的。
  • 热力学第二定律：
  • 标准摩尔熵变（$\Delta_{\mathrm{r}} \mathrm{S}_{\mathrm{m}}^{\theta}(\mathrm{T}$)，熵的生成物-反应物，单位$J\cdot mol^{-1}\cdot K^{-1}$）
  • $\Delta S$在数值上为恒温、可逆过程中体系吸收的能量$Q_r$与热传递时温度的比值，即
  • 熵增原理

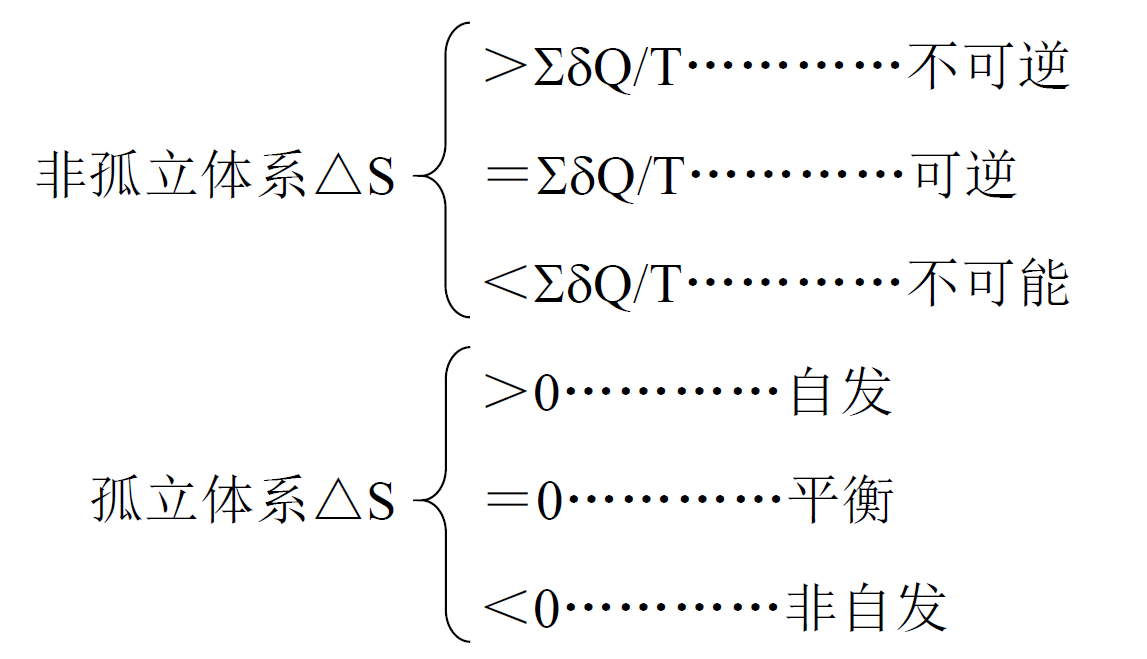
  • 吉布斯自由能：

    • 定义：$G=H-TS$
    • 在等温等压条件下，体系吉布斯自由能的减少，等于体系所能对环境做的最大有用功（$-W_非$），即吉布斯自由能的减小可表征体系做非体积功的能力。
    • 封闭体系中化学反应在等温等压且$W_非=0$条件下，
    • 标准生成吉布斯自由能$\Delta_{\mathrm{f}} \mathrm{G}_{\mathrm{m}}^{\theta}(\mathrm{T})$
    • 关系式：$\Delta_{\mathrm{r}} \mathrm{G}_{\mathrm{m}}^{\theta}=\Delta_{\mathrm{r}} \mathrm{H}_{\mathrm{m}}^{\theta}-T\Delta_{\mathrm{r}} \mathrm{S}_{\mathrm{m}}^{\theta}$

  • 可逆反应

  • 平衡常数
    • 浓度经验平衡常数
    • 压力经验平衡常数
    • 标准状态浓度$c^{\theta}=1mol\cdot dm^{-3}$
    • 标准压力$p^{\theta}=100kPa$
    • 标准平衡常数
  • $\Delta_{\mathrm{r}} \mathrm{G}_{\mathrm{m}}=\Delta_{\mathrm{r}} \mathrm{G}_{\mathrm{m}}^{\theta}+RT\ln{Q}$
  • $\Delta_{\mathrm{r}} \mathrm{G}_{\mathrm{m}}^{\theta}=-RT\ln{K^{\theta}}$
  • $\Delta_{\mathrm{r}} G_{\mathrm{m}}=R T \ln \left(\frac{Q}{K^{\ominus}}\right)$
  • $\ln \left(\frac{K_{2}^{\ominus}}{K_{1}^{\ominus}}\right)=\frac{\Delta_{\mathrm{r}} H_{\mathrm{m}}^{\ominus}}{R} \cdot \frac{T_{2}-T_{1}}{T_{1} T_{2}}$
  • 混淆分析
    Q：吉布斯自由能变和标准吉布斯自由能变的区别在哪里？
    A：在化学反应中,标准吉布斯自由能是指所有反应物和产物都是1mol/L,若是气体则都是100kPa下的吉布斯自由能变,它只是温度的函数,而当温度一定时,它的值就定了。而吉布斯自由能变则是指任意状态下,反应物和产物的浓度都不定,压力也都不定,代表化学反应进行到任意程度,它的值决定化学反应的方向。所以标准摩尔吉布斯自由能变只是一个唯一点；而吉布斯自由能变则是变化中的任意点。
  • 化学反应速率
    • 活化能
    • 碰撞理论
    • 反应速率方程
    • 温度对反应速率的影响
    • 阿累尼乌斯公式的应用——通过实验求得活化能（待补充）

第五章 水溶液中的酸碱平衡和配位平衡

  • 相图
  • 超临界现象
    • 超临界流体的特点：
      • 不具备可压缩性(液体)
      • 会充满整个容器(气体)
    • 超临界流体的应用
      • 超临界CO,提取香料、色素、有机反应介质
      • 超临界水中的有机物质在氧或过氧化氢的作用下可以被完全氧化和水解。处理有机污染。
  • 饱和蒸气压的定义：
  • 拉乌尔定律：当温度一定时，难挥发溶质的稀溶液的蒸气压下降值与溶质的摩尔分数成正比，而与溶质的本性无关，可表示如下：
  • 沸点$T_b$
    • 稀溶液沸点升高：
    • $\Delta T_b=T_b-T_b^0$
    • $\Delta T_b=K_bm$
    • （m为质量摩尔浓度，$K_b$为该溶剂的摩尔沸点升高常数）
    • 当$T=T_b$时，气-液共存
  • 凝固点$T_f$
    • 稀溶液沸点下降：
    • $\Delta T_f=T_f^0-T_f$
    • $\Delta T_f=K_fm$
    • （m为质量摩尔浓度，$K_f$为该溶剂的摩尔凝固点下降常数）
    • 当$T=T_f$时，液-固共存

  • 难挥发的非电解质的稀溶液的依数性

    • 溶液比纯溶剂
      • 沸点升高
      • 蒸气压下降
      • 凝固点下降
      • 渗透压现象

  • 渗透压的定义：对于两侧水溶液浓度不同的半透膜，为了阻止水从低浓度一侧渗透到高浓度一侧而在高浓度一侧施加的最小额外压强称为渗透压。

    • 范托夫公式（渗透压公式）
      • $\Pi=\frac{n}{V} RT=cRT$
      • 适用范围：难挥发的非电解质的稀溶液
    • 范德霍夫修正因子
      • 修正因子$i=\frac{实验测得\Delta T_f}{计算推测\Delta {T’}_f}$
      • $\Delta P=i [x_{溶质}P^0_{溶剂}]$
      • $\Delta T_{\mathrm{f}}=i K_{\mathrm{f}} m$
      • $\Delta T_{\mathrm{b}}=i K_{\mathrm{b}} m$
      • $\Pi=i \cdot[c R T]$

  • 酸碱理论的发展

    • 阿伦尼乌斯的电离理论
    • 酸碱质子理论
    • 酸碱电子理论

  • 稀释定律：氢离子浓度等于根号kc

    • 条件：$c K_{\mathrm{a}_{1}} \geqslant 20 K_{\mathrm{w}}, \frac{c}{K_{\mathrm{a}_{1}}} \geqslant 500, \frac{2 K_{\mathrm{a}_{2}}}{\sqrt{c K_{\mathrm{a}_{1}}}} \ll 1$
  • 缓冲溶液
    • $\left[\mathrm{H}^{+}\right]=K_{\mathrm{a}} \frac{c_{\mathrm{HA}}}{c_{\mathrm{A}^{-}}}$
    • $\mathrm{pH}=p K_{\mathrm{a}}+\lg \frac{c_{\mathrm{A}^{-}}}{c_{\mathrm{HA}}}$