此处只会列出最精华的公式、结论部分，基本知识和解题技巧请熟稔于心！

一、最最最重要的三角公式

万能公式

$ \sin^2\alpha=\frac{\tan^2\alpha}{\tan^2\alpha+1} $

$ \cos^2\alpha=\frac{1}{\tan^2\alpha+1} $

$ \sin\alpha\cos\alpha=\frac{\tan\alpha}{\tan^2\alpha+1} $

$ \sin\alpha+\cos\alpha=\pm \sqrt{\frac{(\tan\alpha+1)^2}{\tan^2\alpha+1}} $

$ \sin\alpha-\cos\alpha=\pm \sqrt{\frac{(\tan\alpha-1)^2}{\tan^2\alpha+1}} $

$ \tan^2\alpha=\frac{1-\cos^2\alpha}{\cos^2\alpha}=\frac{\sin^2\alpha}{1-\sin^2\alpha} $​

辅助角公式

$ a\sin\alpha+b\cos\alpha=\sqrt{a^2+b^2}\sin(\alpha+\varphi) $

其中$\tan\varphi=\frac{b}{a}$ ，不等式形式取等时$\tan\alpha=\frac{a}{b}$

诱导公式完整版

• 整圈不变
  $\sin ( x + 2 \pi ) = \sin x , \cos ( x + 2 \pi ) = \cos x$
• 半圈相反
  $\sin ( x + \pi ) = - \sin x, \cos ( x + \pi ) = - \cos x$
• 加直求导
  $\sin ( x + \frac { \pi }{ 2 } ) = \cos x , \cos ( x + \frac { \pi }{ 2 } ) = - \sin x$
• 减直积分
  $\sin ( x - \frac { \pi }{ 2 } ) = \sin ( x + \frac { 3 \pi }{ 2 } ) = - \cos x$
  $\cos ( x - \frac { \pi }{ 2 } ) = \cos ( x + \frac { 3 \pi }{ 2 } ) = \sin x$
• 正奇余偶
  $\sin ( - x ) = - \sin x,\cos ( - x ) = \cos x$
• 正余互余
  $\sin ( \frac { \pi }{ 2 } - x ) = \cos x , \cos ( \frac { \pi }{ 2 } - x ) = \sin x $
  $\tan ( \frac { \pi }{ 2 } - x ) = \cot x,\cot ( \frac { \pi }{ 2 } - x ) = \tan x $
• 切直负变
  $\tan ( x + \frac { \pi }{ 2 } ) = - \cot x , \cot ( x + \frac { \pi }{ 2 } ) = - \tan x$

诱导公式口诀（官方版）

奇变偶不变，符号看象限。

诱导公式口诀（Teruteru版）

加减$\pi$，$\sin,\cos$变

加减负号，$\sin,\tan$变

加$\frac{\pi}{2}$，$\sin,\tan$变

减$\frac{\pi}{2}$，$\cos,\tan$变

二倍角公式

$$\begin{align} \\ \sin 2\alpha &= 2\sin\alpha\cos\alpha \\ &= \frac{2\tan\alpha}{1+\tan^2\alpha} \\ \\ \cos 2\alpha &= 2\cos^{2}\alpha-1 \\ &= 1-2\sin^{2}\alpha \\ &=\cos^{2}\alpha-\sin^{2} \alpha \\ &=(\cos\alpha+\sin\alpha)(\cos\alpha-\sin\alpha) \\ &=\frac{1-\tan^2\alpha}{1+\tan^2\alpha} \\ \\ \tan 2\alpha &=\frac{2\tan\alpha}{1-\tan^{2}\alpha} \end{align}$$

半角公式

$ \sin^{2}\frac{\alpha}{2}=\frac{1-\cos\alpha}{2} $

$ \cos^{2}\frac{\alpha}{2}=\frac{1+\cos\alpha}{2} $

$ \tan^{2}\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha} $

和差角公式

$\cos (\alpha \pm \beta)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$

$\sin (\alpha \pm \beta)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$

$ \tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} $

*三倍角公式

$ \sin 3\alpha=3\sin\alpha-4\sin^3\alpha $

$ \cos 3\alpha=4\cos^3\alpha-3\cos\alpha $

$ \tan 3\alpha=\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^{2}\alpha} $

*积化和差、和差化积

$\cos \alpha \cos \beta=\frac{1}{2}[\cos (\alpha+\beta)+\cos (\alpha-\beta)]$

$\sin \alpha \sin \beta=-\frac{1}{2}[\cos (\alpha+\beta)-\cos (\alpha-\beta)]$

$\sin \alpha \cos \beta=\frac{1}{2}[\sin (\alpha+\beta)+\sin (\alpha-\beta)]$

$\cos \alpha \sin \beta=\frac{1}{2}[\sin (\alpha+\beta)-\sin (\alpha-\beta)]$

$ \sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} $

$ \sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2} $

$ \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} $

$ \cos\alpha-\cos\beta=2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2} $

一些奇怪的公式

$ 1\pm \sin 2\alpha=(\sin\alpha\pm\cos\alpha)^2 $

$ \tan\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{1-\cos\alpha}{\sin\alpha} $

$ 4\sin\alpha\cdot\sin(\frac{\pi}{3} -\alpha)\cdot\sin(\frac{\pi}{3} +\alpha)=\sin3\alpha $

$ 4\cos\alpha\cdot\cos(\frac{\pi}{3} -\alpha)\cdot\cos(\frac{\pi}{3} +\alpha)=\cos3\alpha $

$ \tan(\frac{\pi}{4}+\alpha)\cdot\tan(\frac{\pi}{4}-\alpha)=\frac{1+\tan\alpha}{1-\tan\alpha}\cdot\frac{1-\tan\alpha}{1+\tan\alpha}=1 $

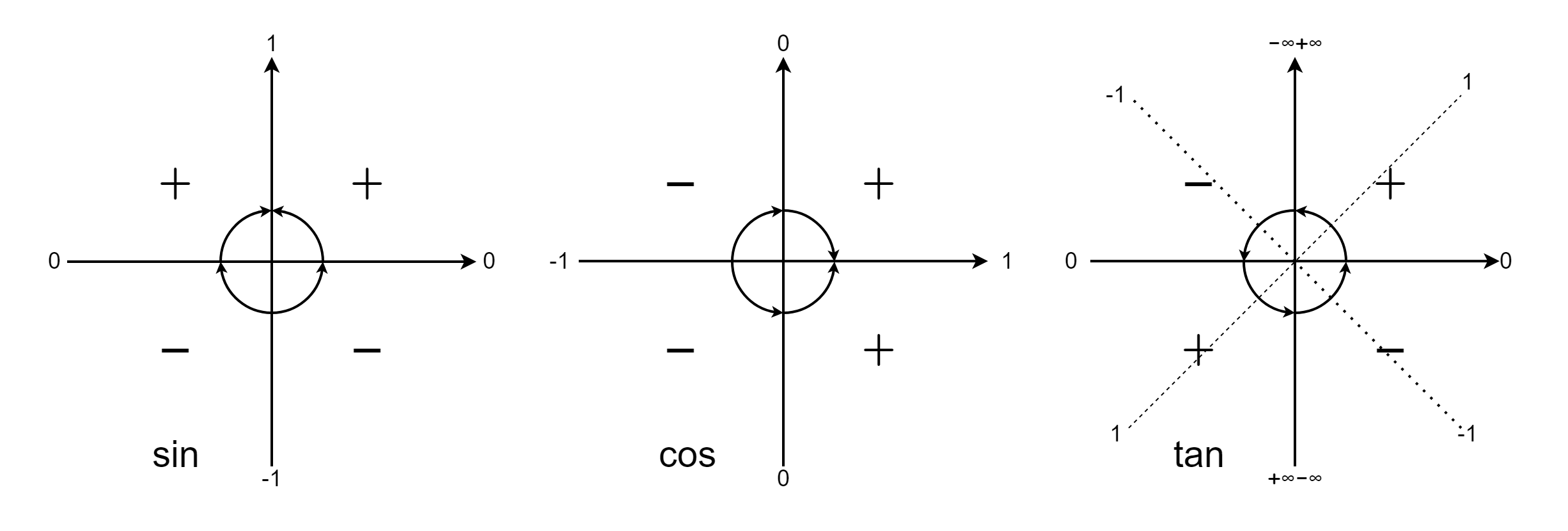
象限图

二、数列相关

常见裂项、放缩

1. $ \frac{1}{n(n+k)}=\frac{1}{k}\left(\frac{1}{n}-\frac{1}{n+k}\right) $
2. $ \frac{1}{n(n+1)(n+2)}=\frac{1}{2}\left(\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)}\right) $
3. $ \frac{1}{(2n-1)(2n+1)}=\frac{1}{2}\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right) $
4. $ \frac{1}{\sqrt{n}+\sqrt{n+k}}=\frac{1}{k}\left(\sqrt{n+k}-\sqrt{n}\right) $
5. $ \sum^{n}_{i=1}\left(2i-1\right)=n^2 $
6. $ \sum^{n}_{i=1} i^3=\left[\frac{n(n+1)}{2}\right]^2=\left(\sum^{n}_{i=1} i\right)^2 $
7. $ \frac{1}{2^n-1}\le\frac{1}{2^{n-1}} $
8. $ \frac{1}{(2n-1)^2}<\frac{1}{4n(n-1)}=\frac{1}{4}\left(\frac{1}{n-1}-\frac{1}{n}\right) $
9. $ \frac{1}{n^3}<\frac{1}{n(n^2-1)}={1 \over 2}\left[\frac{1}{(n-1)n}-\frac{1}{n(n+1)}\right] $
10. $ 2(\sqrt{n+1}-\sqrt{n})=\frac{2}{\sqrt{n+1}+\sqrt{n}}<{1\over \sqrt{n}}<\frac{2}{\sqrt{n}+\sqrt{n-1}}=2(\sqrt{n}-\sqrt{n-1}) $
11. $ \frac{2n-1}{2n}<\sqrt{\frac{2n-1}{2n+1}}, \frac{2n}{2n-1}>\sqrt{\frac{2n+1}{2n-1}}$
12. $ \frac{n^2}{4n^2-1}={1\over 4}+{1\over 8}\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right) $
13. $ \frac{1}{n\sqrt{n}}<2\left(\frac{1}{\sqrt{n-1}}-\frac{1}{\sqrt{n}}\right) $
14. $ n\cdot n!=(n+1)!-n! $
15. $ \frac{n}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!} $
16. $ {1\over \sqrt{n}}<\sqrt{2}(\sqrt{2n+1}-\sqrt{2n-1}) $

不动点法

暂略

等比数列与等差数列相乘

• [ ] 错位相减（最垃圾的方法，不用管它）
• [ ] 背公式（太复杂）
• [x] 待定系数法（熟练运用）
• [x] 裂项（最好的方法，必须会）

三、排列组合

各类基本方法

不多解释

小球入盒模型

点击进入

环形染色问题

$ ans=(m-1)(-1)^n+(m-1)^n $

四、基本不等式

*均值不等式

$$\begin{array}{c} 若a_{n}\ge 0，\\ H_{n}=\frac{n}{\sum \limits_{i=1}^{n}\frac{1}{a_{i}}}= \frac{n}{\frac{1}{a_{1}}+ \frac{1}{a_{2}}+ \cdots + \frac{1}{a_{n}}} \\ G_{n}=\sqrt[n]{\prod \limits_{i=1}^{n}a_{i}}= \sqrt[n]{a_{1}a_{2}\cdots a_{n}} \\ A_{n}=\frac{1}{n}\sum \limits_{i=1}^{n}a_{i}=\frac{a_{1}+ a_{2}+ \cdots + a_{n}}{n} \\ Q_{n}=\sqrt{\sum \limits_{i=1}^{n}a_{i}^{2}}= \sqrt{\frac{a_{1}^{2}+ a_{2}^{2}+ \cdots + a_{n}^{2}}{n}} \\ H_{n}\leq G_{n}\leq A_{n}\leq Q_{n} \end{array}$$

均值不等式的二元形式

$$\frac{2}{\frac{1}{a}+\frac{1}{b}}\le\sqrt{ab}\le\frac{a+b}{2}\le\sqrt{\frac{a^2+b^2}{2}}$$

均值不等式二元形式变形

（写在小抄上就很方便）

$$\left\{ \begin{aligned} a+b\ge&2\sqrt{ab} \\ a+b\ge&\frac{4}{\frac{1}{a}+\frac{1}{b}} \\ a+b\le&\sqrt{2}\sqrt{a^2+b^2} \end{aligned} \right.$$ $$\left\{ \begin{aligned} ab\le&\frac{(a+b)^2}{4} \\ ab\ge&\frac{4}{(\frac{1}{a}+\frac{1}{b})^2} \\ ab\le&\frac{a^2+b^2}{2} \end{aligned} \right.$$ $$\left\{ \begin{aligned} \frac{1}{a}+\frac{1}{b}\ge&\frac{4}{a+b} \\ \frac{1}{a}+\frac{1}{b}\ge&\frac{2}{\sqrt{ab}} \\ \frac{1}{a}+\frac{1}{b}\ge&\frac{2\sqrt{2}}{\sqrt{a^2+b^2}} \end{aligned} \right.$$ $$\left\{ \begin{aligned} a^2+b^2\ge&\frac{(a+b)^2}{2} \\ a^2+b^2\ge&2ab \\ a^2+b^2\ge&\frac{8}{(\frac{1}{a}+\frac{1}{b})^2} \end{aligned} \right.$$

其他不等式

（待更新）
1.柯西
2.排序
3.切比雪夫
4.卡尔松

五、立体几何&平面几何（主要是三角形）

体积万能公式

$ V=\frac{1}{6}\left(S_{顶}+S_{底}+4S_{中}\right)h $

三角形秦九韶公式

$ S=\frac{1}{4}\sqrt{4a^2b^2-(a^2+b^2-c^2)^2} $
(注意此式为三元对称式)

斯特瓦尔特定理

$$d=\sqrt{\frac{a^2y+b^2x}{x+y}-xy}$$

(看清楚公式和图再记，$a^2y+b^2x$千万别搞错)

一些三角形小定理

$ \Delta ABC中，a^2=b(b+c)\Leftrightarrow A=2B $

$ S_{\Delta ABC}=\frac{c^2}{2}\cdot\frac{\tan A\tan B}{\tan A+\tan B} $

$ \Delta ABC中，2b=a+c \Leftrightarrow \tan\frac{A}{2}\tan\frac{B}{2}=\frac{1}{3}$

正四面体相关

$ S_{截}=\frac{\sqrt{2}}{4}a^2, S_{表}=\sqrt{3}a^2, V=\frac{\sqrt{2}}{12}a^3 $
$ h=\frac{\sqrt{6}}{3}a, r=\frac{\sqrt{6}}{12}a, R=\frac{\sqrt{6}}{4}a $

对棱中点连线长$\frac{\sqrt{2}}{2}a$

线面角：$\sin\theta=\frac{\sqrt{6}}{3}, \cos\theta=\frac{\sqrt{3}}{3}, 1:\sqrt{2}:\sqrt{3} $

二面角：$\sin\alpha=\frac{2\sqrt{2}}{3}, \cos\alpha=\frac{1}{3}, 1:2\sqrt{2}:3 $

三射线定理&Teruteru线面角终极公式

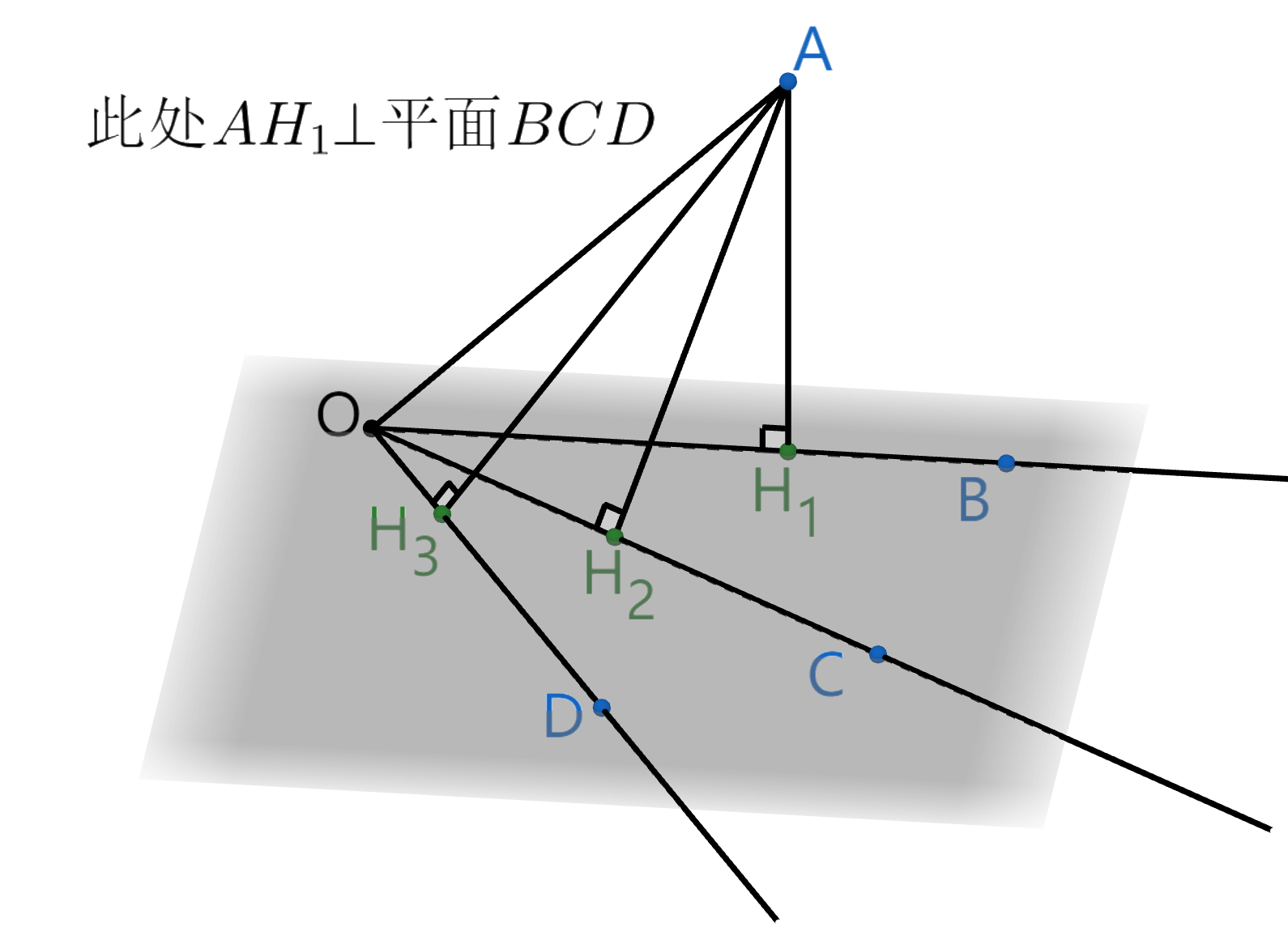
三射线定理：$\angle AOC=\alpha, \angle AOB=\beta,\angle BOC=\theta, 二面角C-OA-B=\gamma, 则：$

$$\cos\gamma=\frac{\cos\theta-\cos\alpha\cos\beta}{\sin\alpha\sin\beta}$$

Teruteru线面角终极公式：$\cos\angle AOH_2=a, \cos\angle AOH_3=b, \cos\angle COD=c, 则： $

$$\cos\angle AOH_1=\sqrt{\frac{a^2+b^2-2abc}{1-c^2}}$$

其他公式

四面体$ABCD$对棱$AB、BD$所成角为$\alpha$，则：

$$\cos\alpha=\frac{\left|AB\right|^2+\left|CD\right|^2-\left|AD\right|^2-\left|BC\right|^2}{2\left|AC\right|\cdot\left|BD\right|}$$

$AC、BD$距离为$d$, 则

$$V_{ABCD}=\frac{\left|AC\right|\left|BD\right|d\sin\alpha}{6}$$

六、解析几何

常用结论

★1.点$(x_1,y_1)$关于直线$Ax+By+C=0$的对称点坐标：

$$\left(x_1-\frac{2A(Ax_1+By_1+C)}{A^2+B^2},y_1-\frac{2B(Ax_1+By_1+C)}{A^2+B^2}\right)$$

垂足坐标：

$$\left(x_1-\frac{A(Ax_1+By_1+C)}{A^2+B^2},y_1-\frac{B(Ax_1+By_1+C)}{A^2+B^2}\right)$$

2.直线$Ax+By+C=0$关于点$(x_0,y_0)$对称的直线方程为：

$$Ax+By-2(Ax_0+By_0)-C=0$$

*3.直线$A_1x+B_1y+C_1=0$关于直线$A_0x+B_0y+C_0=0$对称的直线：

$$(A_1A_0^2-A_1B_0^2+2B_0B_1A_0)x+(B_1B_0^2-B_1A_0^2+2A_0A_1B_0)y+(2A_1A_0C_0+2B_1B_0C_0-C_1A_0^2-C_1B_0^2)=0$$

★4.以点$(x_1,y_1),(x_2,y_2)$为端点的线段的中垂线为：

$$2(x_1-x_2)x+2(y_1-y_2)y+(y_2^2-y_1^2+x_2^2-x_1^2)=0$$

5.点$(x_1,y_1)$关于点$(x_0,y_0)$顺时针旋转$\theta$所得点：

$$\left((x_1-x_0)\cos\theta+(y_1-y_0)\sin\theta+x_0,(x_1-x_0)\cos\theta+(y_1-y_0)\sin\theta+y_0\right)$$

6.三角形“七心”

$$\begin{array}{c} 重心G\left(\frac{\sum x_A}{3},\frac{\sum y_A}{3}\right)\\ 内心I\left(\frac{\sum ax_A}{\sum a},\frac{\sum ay_A}{\sum a}\right)\\ 垂心H\left(\frac{\sum\frac{ax_A}{\cos A}}{\sum\frac{a}{\cos A}},\frac{\sum\frac{ay_A}{\cos A}}{\sum\frac{a}{\cos A}}\right)\\ 内心I\left(\frac{\sum x_A\sin2A}{\sum\sin2A},\frac{\sum y_A\sin2A}{\sum\sin2A}\right)\\ 三个旁心略 \end{array}$$

圆锥曲线——椭圆

点差法结论

$$\begin{array}{l} k_{AB}=-\frac{b^2x_0}{a^2y_0} \\ k_{OP}\cdot k_{AB}=-\frac{b^2}{a^2} \end{array}$$

焦半径公式

$$\begin{array}{l} \left|PF_1\right|=ex_0+a \\ \left|PF_2\right|=-ex_0+a \end{array}$$

通径长：$\frac{2b^2}{a}$

准线：$x=\pm\frac{a^2}{c}$

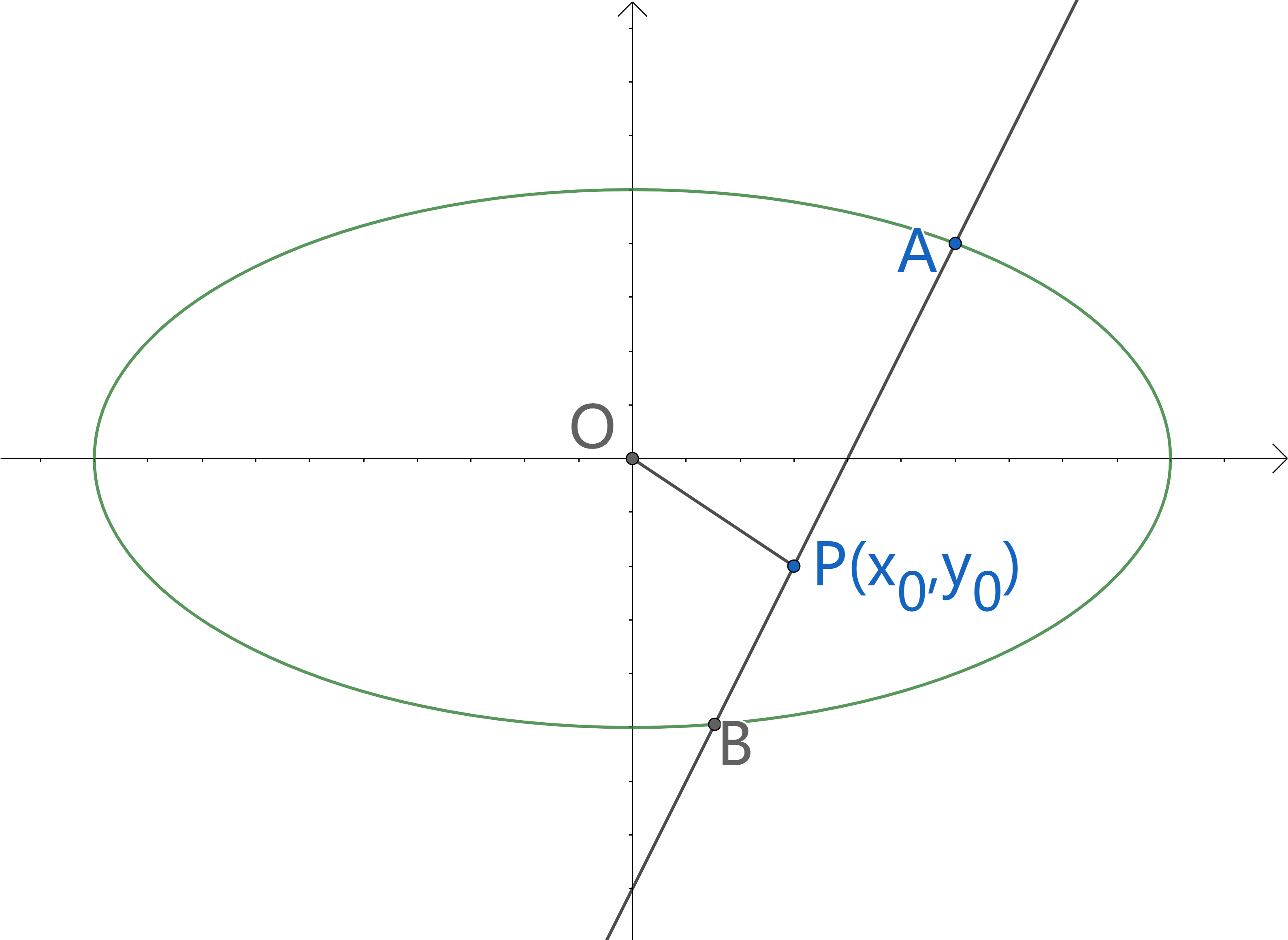
过端点/原点的直线

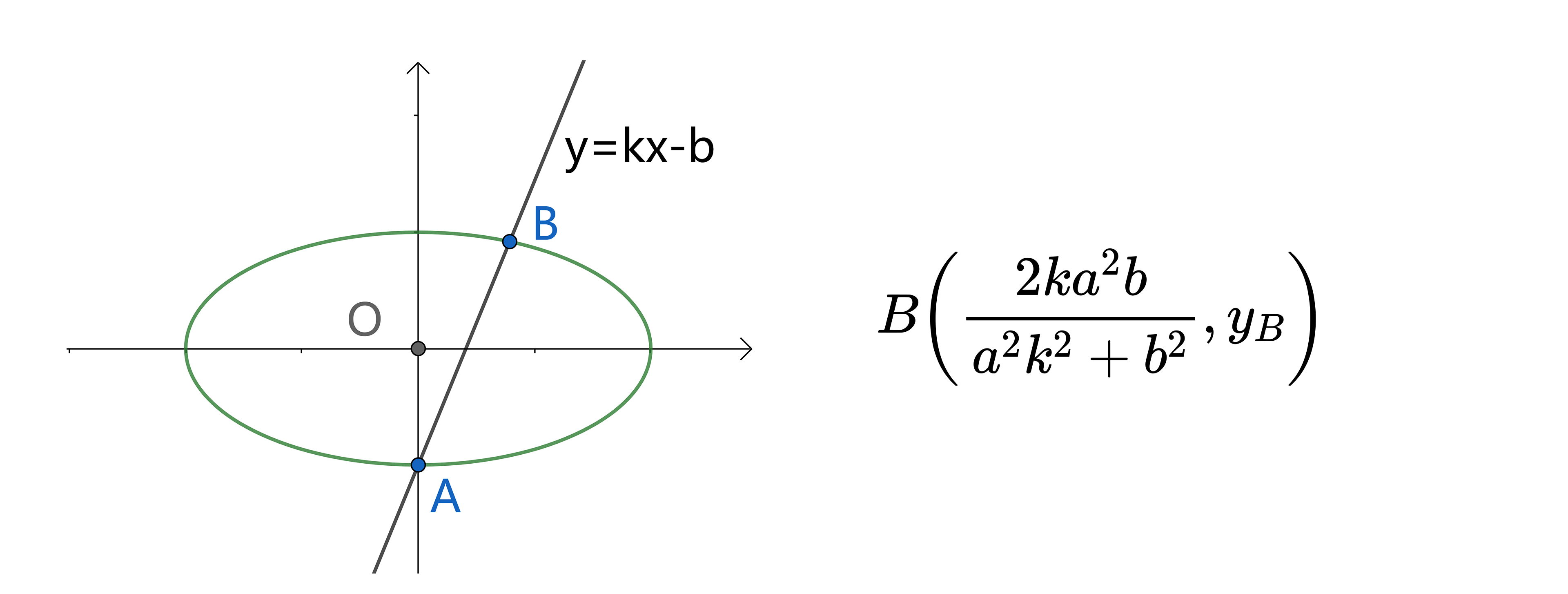
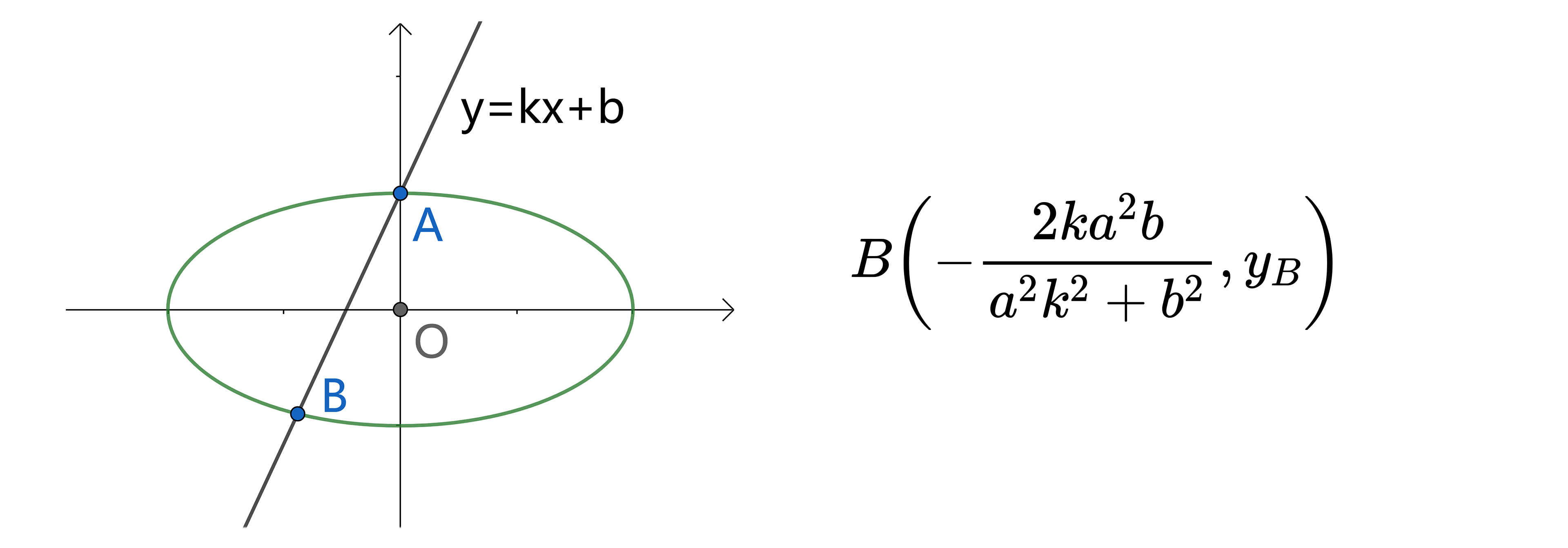
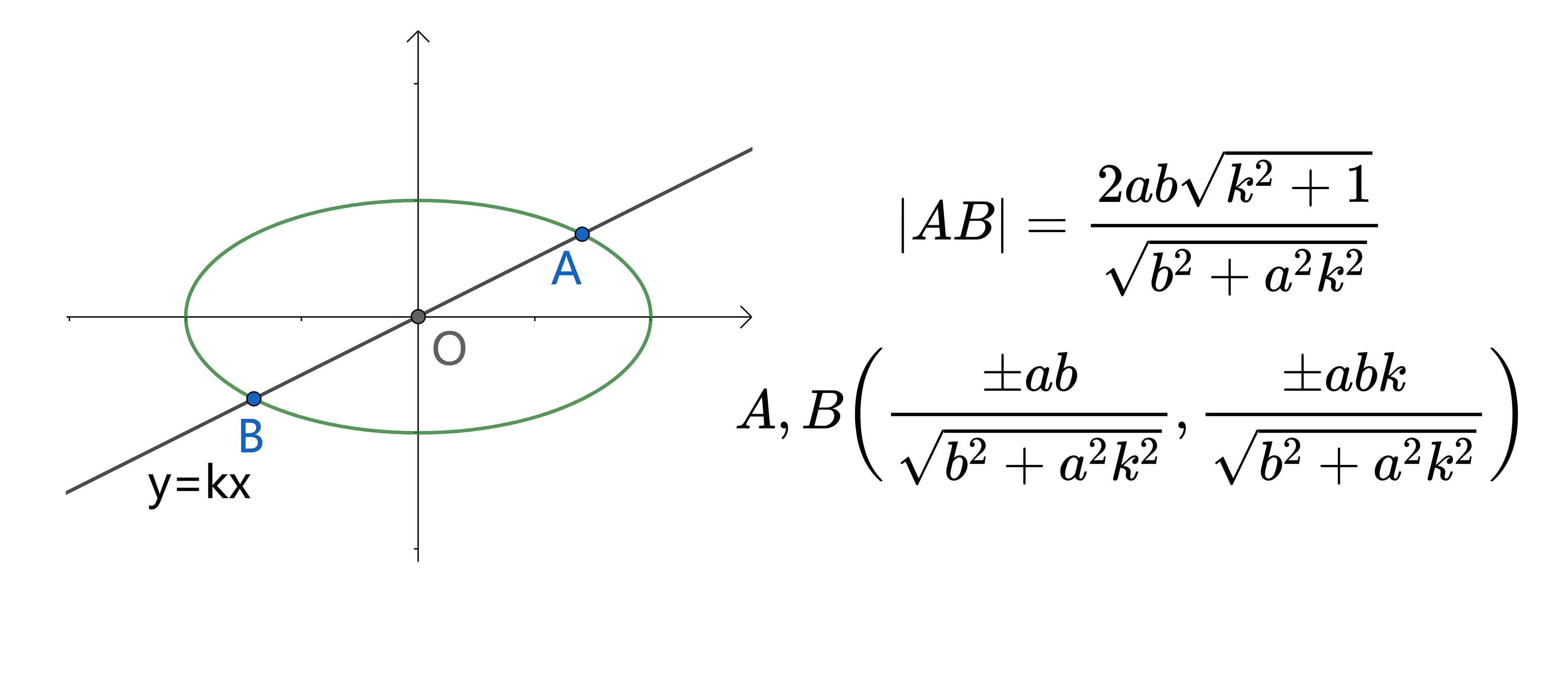
对端点张角的三角形

★过焦点的直线

• $$\left\{ \begin{array}{l} x_1+x_2=\frac{2a^2k^2c}{b^2+a^2k^2} \\ x_1\cdot x_2=\frac{a^2k^2c^2-a^2b^2}{b^2+a^2k^2} \\ \left|x_1-x_2\right|=\frac{2ab^2\sqrt{k^2+1}}{b^2+a^2k^2} \end{array} \right.$$
• $$\left\{ \begin{array}{l} y_1+y_2=\frac{-2b^2ck}{b^2+a^2k^2} \\ y_1\cdot y_2=\frac{-k^2b^4}{b^2+a^2k^2} \\ \left|y_1-y_2\right|=\frac{2ab^2|k|\sqrt{k^2+1}}{b^2+a^2k^2} \end{array} \right.$$

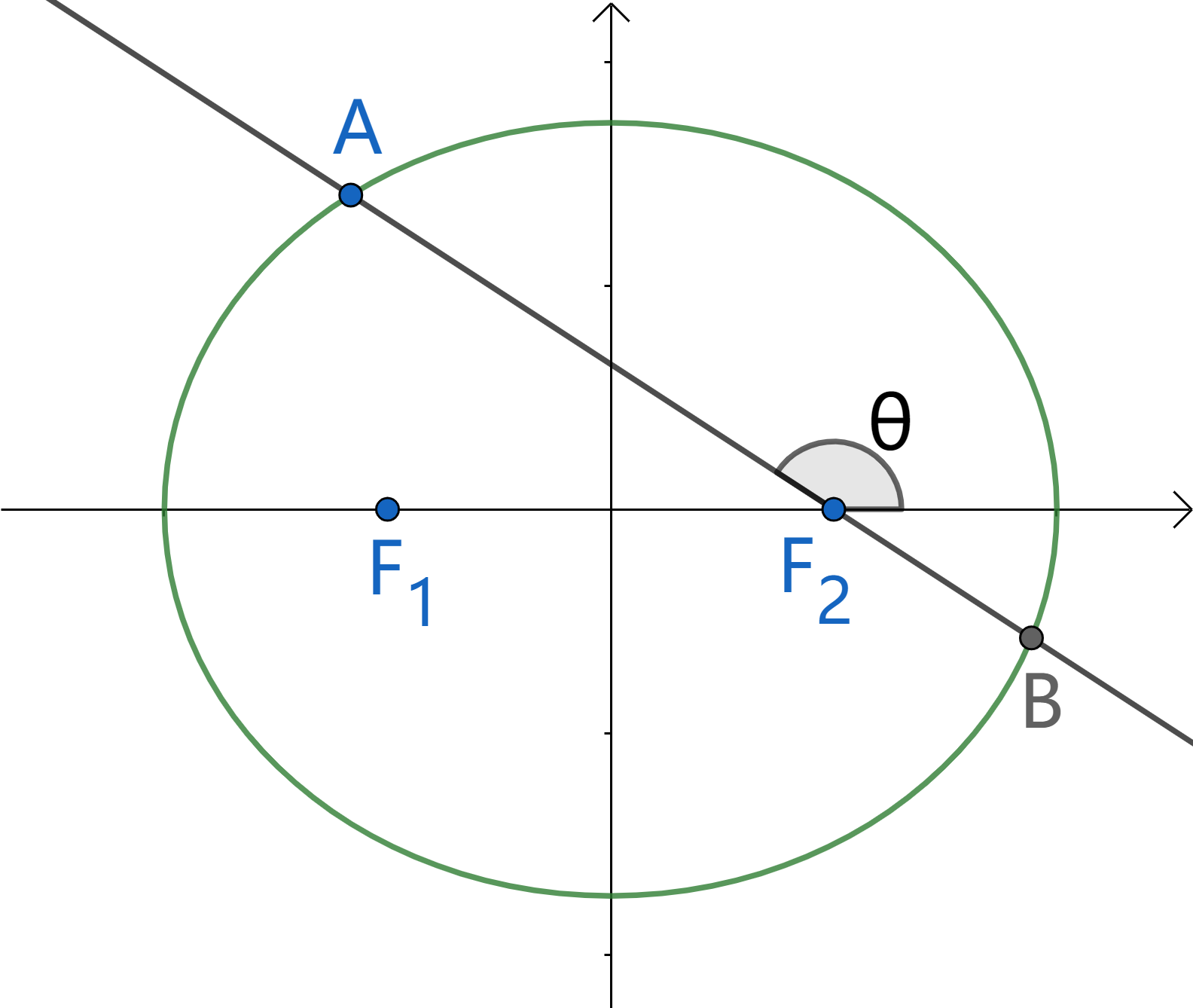
• $\Delta=4a^2b^4(k^2+1)$

• $|AB|=(k^2+1)\frac{2ab^2}{b^2+a^2k^2}=\frac{2ab^2}{a^2-c^2\cos^2\theta}$

• $\overrightarrow{OA}\cdot\overrightarrow{OB}=\frac{a^2k^2c^2-a^2b^2-b^4k^2}{b^2+a^2k^2}$

• $S_{\Delta OAB}=\frac{\sqrt{k^2+1}|ab^2ck|}{b^2+a^2k^2}=\frac{\sqrt{m^2+1}ab^2c}{b^2m^2+a}(m=\frac{1}{k})$

• $|AF_2|\cdot|BF_2|=\frac{b^4(k^2+1)}{b^2+a^2k^2}$

• $\frac{b^4}{a^2}\le |AF_2|\cdot|BF_2| \le b^2$
  （左边$k$不存在时取等，右边$k=0$时取等）

• $|AF_1|\cdot|BF_1|=\frac{(4a^2c^2+b^4)k^2+b^4}{b^2+a^2k^2}$

• $b^2\le |AF_1|\cdot|BF_1| \le \frac{(2a^2-b^2)^2}{a^2}$
  （左边$k=0$时取等，右边$k$不存在时取等）

• $|AF_2|=\frac{b^2}{a+c\cos\theta},|BF_2|=\frac{b^2}{a-c\cos\theta}$

• $\frac{1}{|AF_2|}+\frac{1}{|BF_2|}=\frac{2a}{b^2}$

• 若$|AF_2|=m|BF_2|$，则$(\frac{1-m}{1+m})^2=\frac{e^2}{1+k^2}$（圆锥曲线都成立），
  则$|AB|=\frac{b^2(m+1)^2}{2am}$，$k=\pm\sqrt{\frac{4a^2m-b^2(m+1)^2}{a^2(m-1)^2}}$

不知名的公式

过点$M(x_0,y_0)$作斜率为$k$的直线交椭圆于点$A,B$，则：

$$\overrightarrow{MA}\cdot\overrightarrow{MB}=\frac{(k^2+1)(a^2y_0^2+b^2x_0^2-a^2b^2)}{b^2+a^2k^2}$$

两直线斜率之和/积为定值

设有圆锥曲线$\Gamma$，点$P(x_0,y_0)$在$\Gamma$上，$l$交$\Gamma$于点$A,B$，

• 若$k_{PA}\cdot k_{PB}=\lambda\ne\frac{b^2}{a^2}$

  • 椭圆：$l$过定点$(\frac{\lambda a^2+b^2}{\lambda a^2-b^2}x_0,-\frac{\lambda a^2+b^2}{\lambda a^2-b^2}y_0)$
  • 双曲线：$l$过定点$(\frac{\lambda a^2-b^2}{\lambda a^2+b^2}x_0,-\frac{\lambda a^2-b^2}{\lambda a^2+b^2}y_0)$
  • 抛物线：$l$过定点$(x_0-\frac{2p}{\lambda},-y_0)$

• 若$k_{PA}+k_{PB}=\lambda\ne 0$

  • 椭圆：$l$过定点$(x_0-\frac{2y_0}{\lambda},-\frac{2b^2x_0}{a^2\lambda}-y_0)$
  • 双曲线：$l$过定点$(x_0-\frac{2y_0}{\lambda},\frac{2b^2x_0}{a^2\lambda}-y_0)$
  • 抛物线：$l$过定点$(x_0-\frac{2y_0}{\lambda},\frac{2p}{\lambda}-y_0)$

直线与椭圆相交弦长

$Ax+By+C=0$与$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的相交弦长：

$$l=\sqrt{A^2+B^2}\frac{2ab\sqrt{a^2A^2+b^2B^2-C^2}}{a^2A^2+b^2B^2}$$

对中心张直角的弦

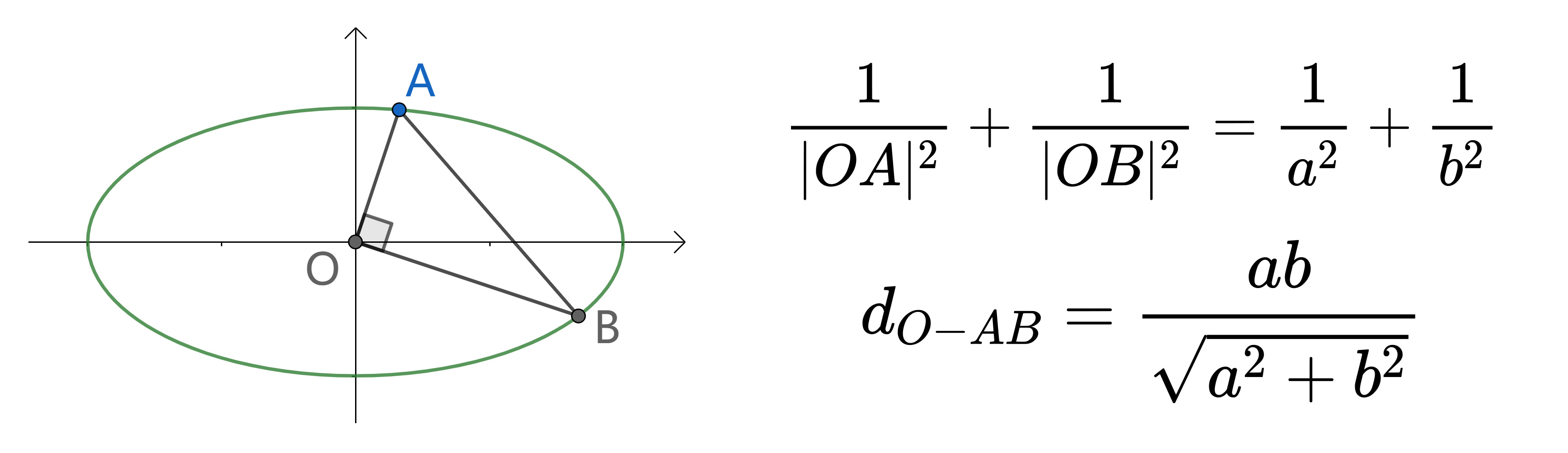
一些等价转换

$$\begin{aligned} & \qquad k_{OM}\cdot k_{ON}=-\frac{b^2}{a^2} \\ & \Leftrightarrow x_1^2+x_2^2=a^2 \\ & \Leftrightarrow y_1^2+y_2^2=b^2 \\ & \Leftrightarrow S_{\Delta OMN}=\frac{ab}{2} \\ & \Leftrightarrow OM^2+ON^2=a^2+b^2 \\ & \Leftrightarrow (\text{若}\overrightarrow{OP}=\lambda\overrightarrow{OM}+\mu\overrightarrow{ON}),\lambda^2+\mu^2=1 \\ & \Leftrightarrow Q\text{在}\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{1}{2}\text{上} \\ & \Leftrightarrow (\text{若}\overrightarrow{OP}=\lambda\overrightarrow{OM}+\mu\overrightarrow{ON}), P\text{在}\frac{x^2}{a^2}+\frac{y^2}{b^2}=\lambda^2+\mu^2\text{上} \end{aligned}$$

more/もっともっと

点击下载

双曲线二级结论

一个特殊三角形

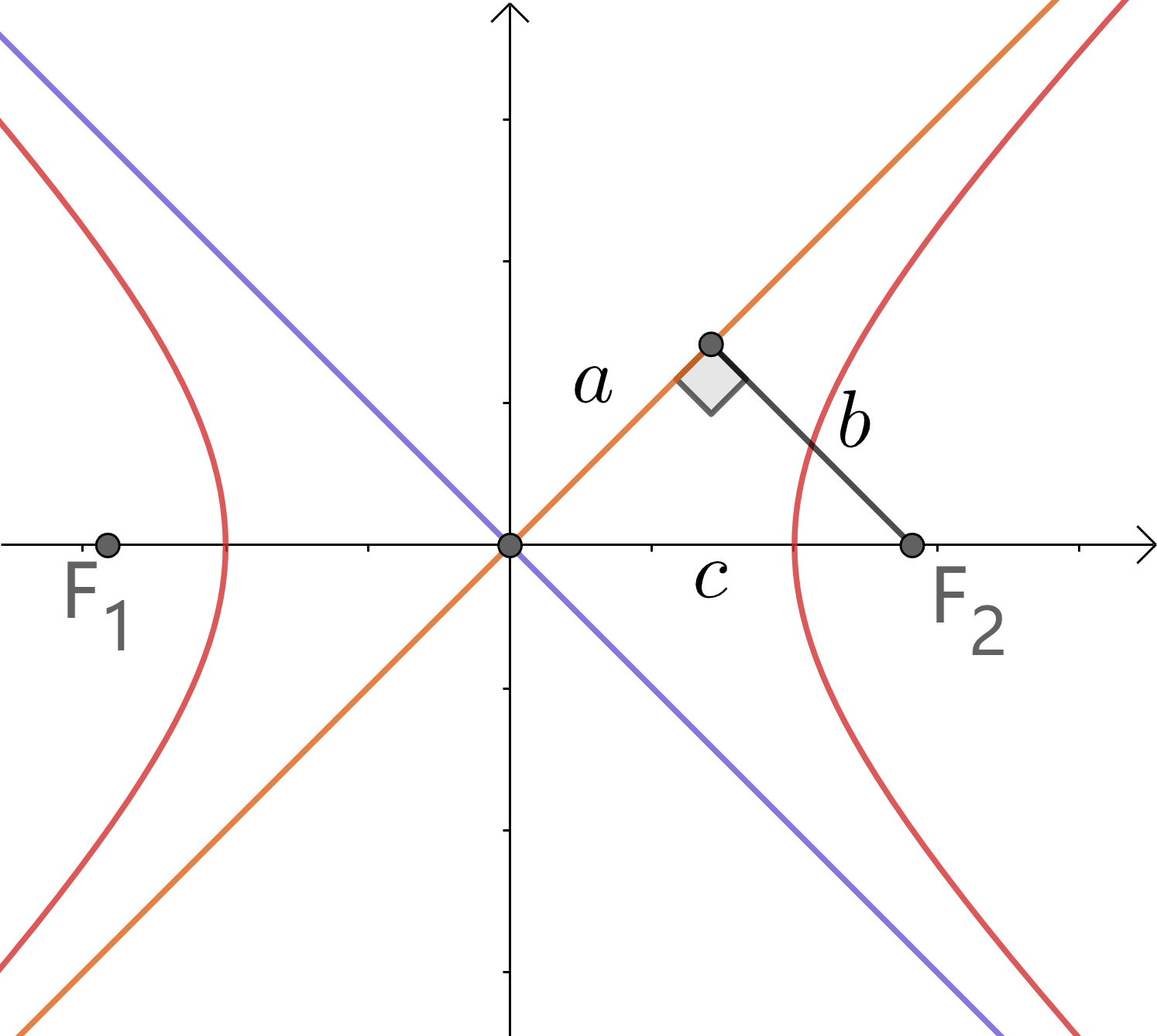
切线与渐近线

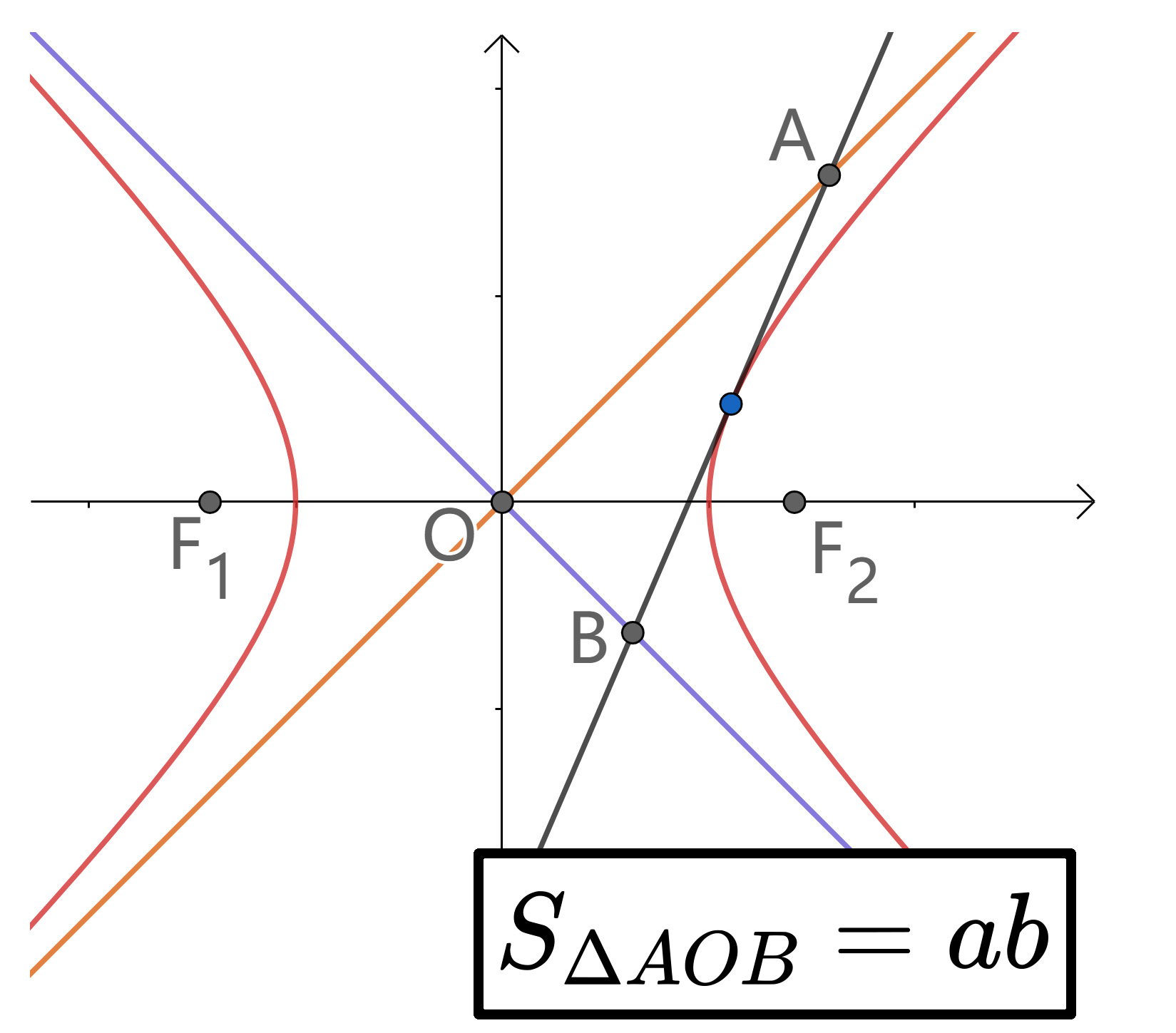
焦半径公式

$$\begin{array}{c} \text{准线：}x=\pm\frac{a^2}{c} \\ |P_1F_1|=ex_0+a \\ |P_1F_2|=ex_0-a \\ |P_2F_1|=-ex_0-a \\ |P_2F_2|=-ex_0+a \\ \end{array}$$

对两焦点张直角

抛物线二级结论

一些基本量

• $$\left\{ \begin{array}{l} x_A+x_B=\frac{p^2}{4} \\ x_A\cdot x_B=\frac{pk^2+2p}{k^2} \end{array} \right.$$
• $$\left\{ \begin{array}{l} y_A+y_B=-p^2 \\ y_A\cdot y_B=\frac{2p}{k} \end{array} \right.$$
• $$\begin{aligned} |AB|&=\frac{2p}{\sin^2\theta} \\ &=2p\cdot\frac{1+k^2}{k^2} \\ &=x_A+x_B+p \end{aligned}$$

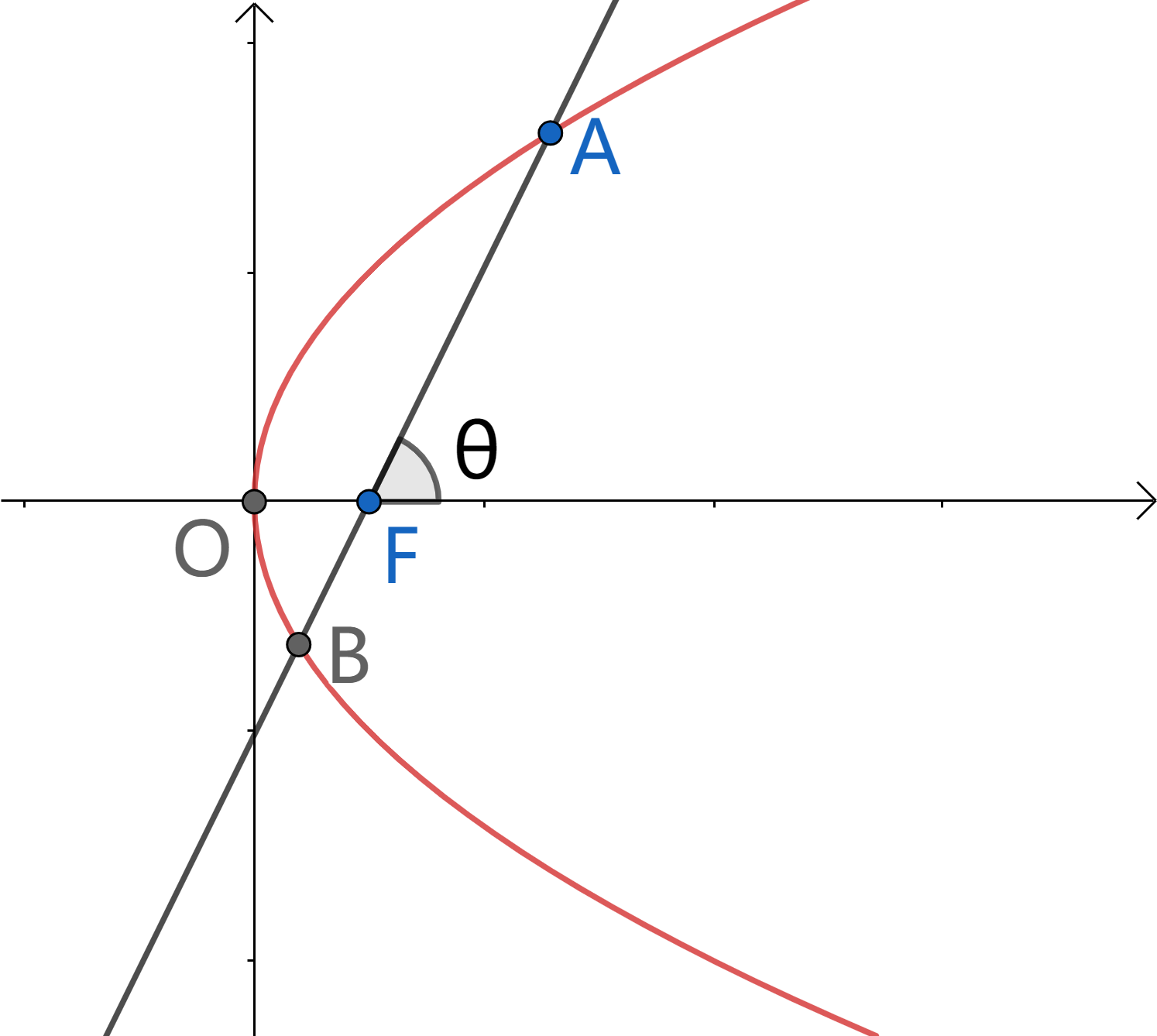
• $|AF|=\frac{p}{1-\cos\theta}$

• $|BF|=\frac{p}{1+\cos\theta}$

• $\frac{1}{|AF|}+\frac{1}{|AF|}=\frac{2}{p}$

• $S_{\Delta AOB}=\frac{p^2}{2\sin\theta}=\frac{p^2}{2}\sqrt{\frac{k^2+1}{k^2}}$

开口向上的

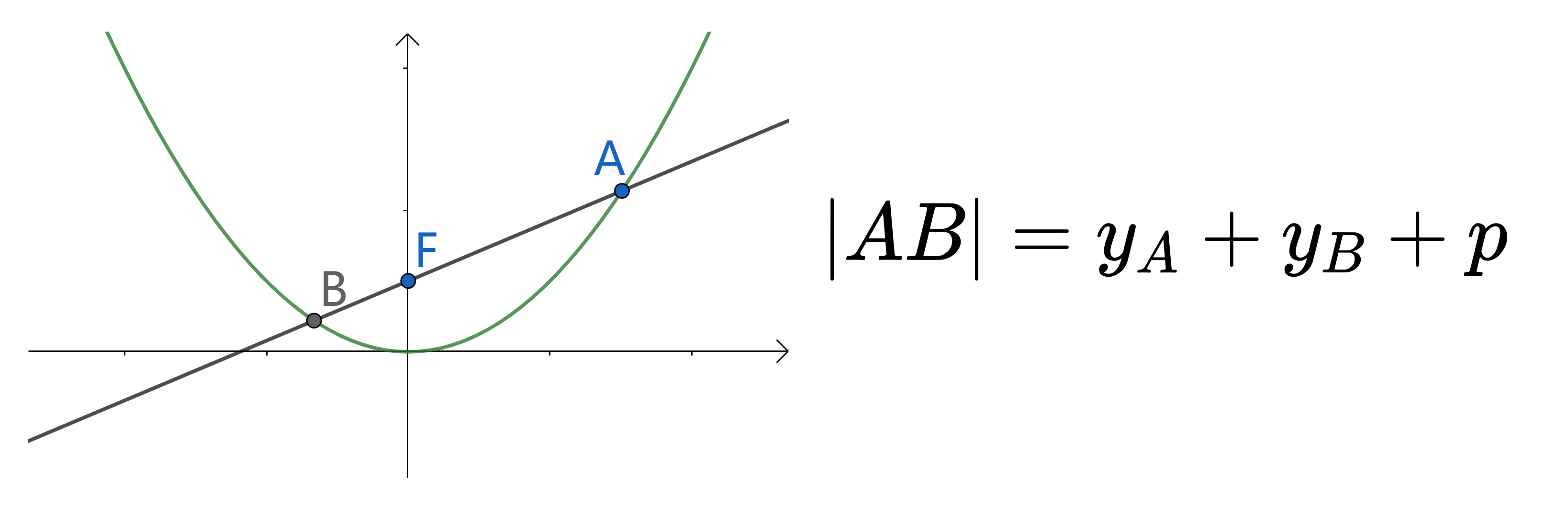
两条过焦点的直线

中垂线

阿基米德三角形

七、导数

$e^x$、$lnx$、$x$ 的基本组合

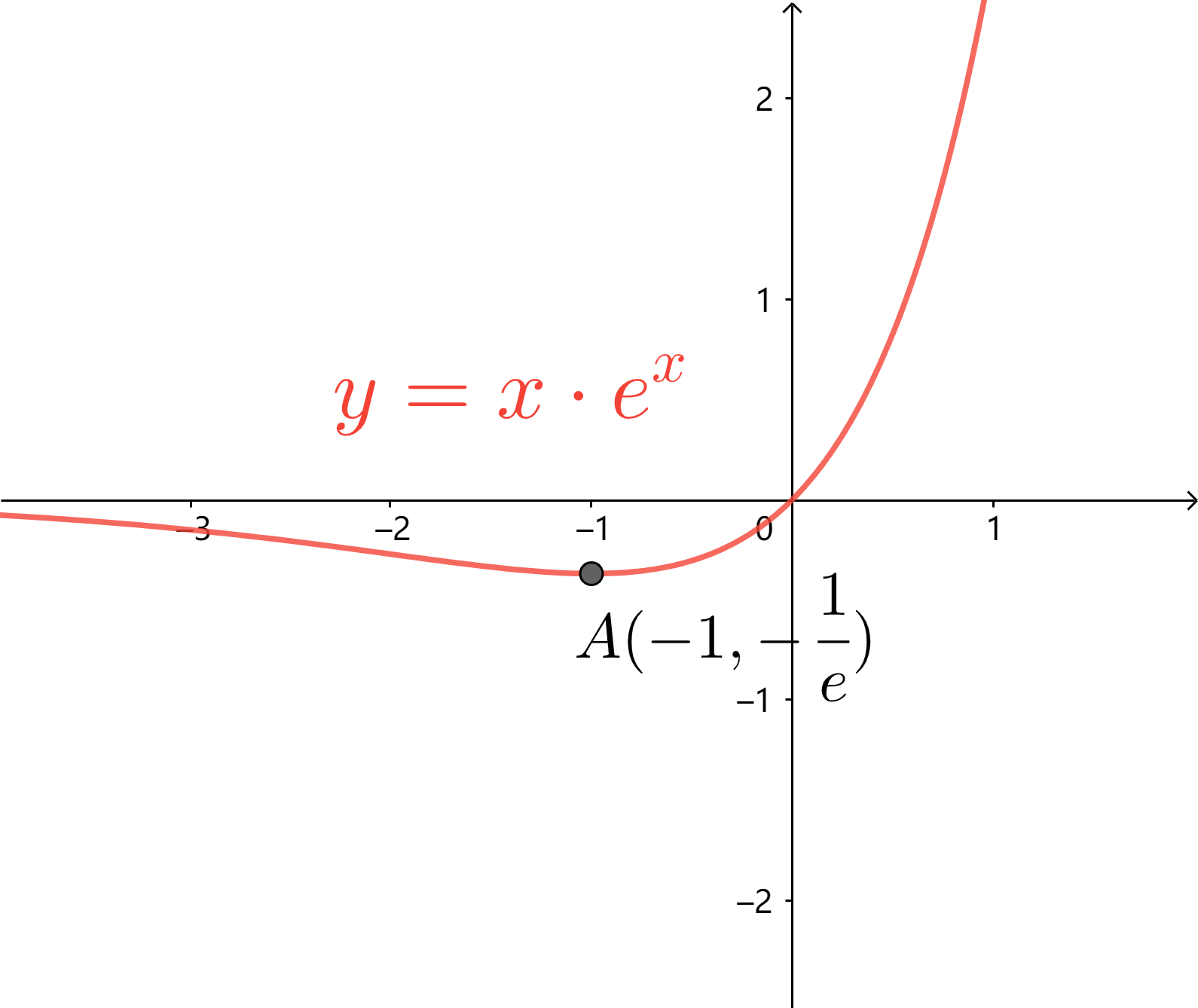
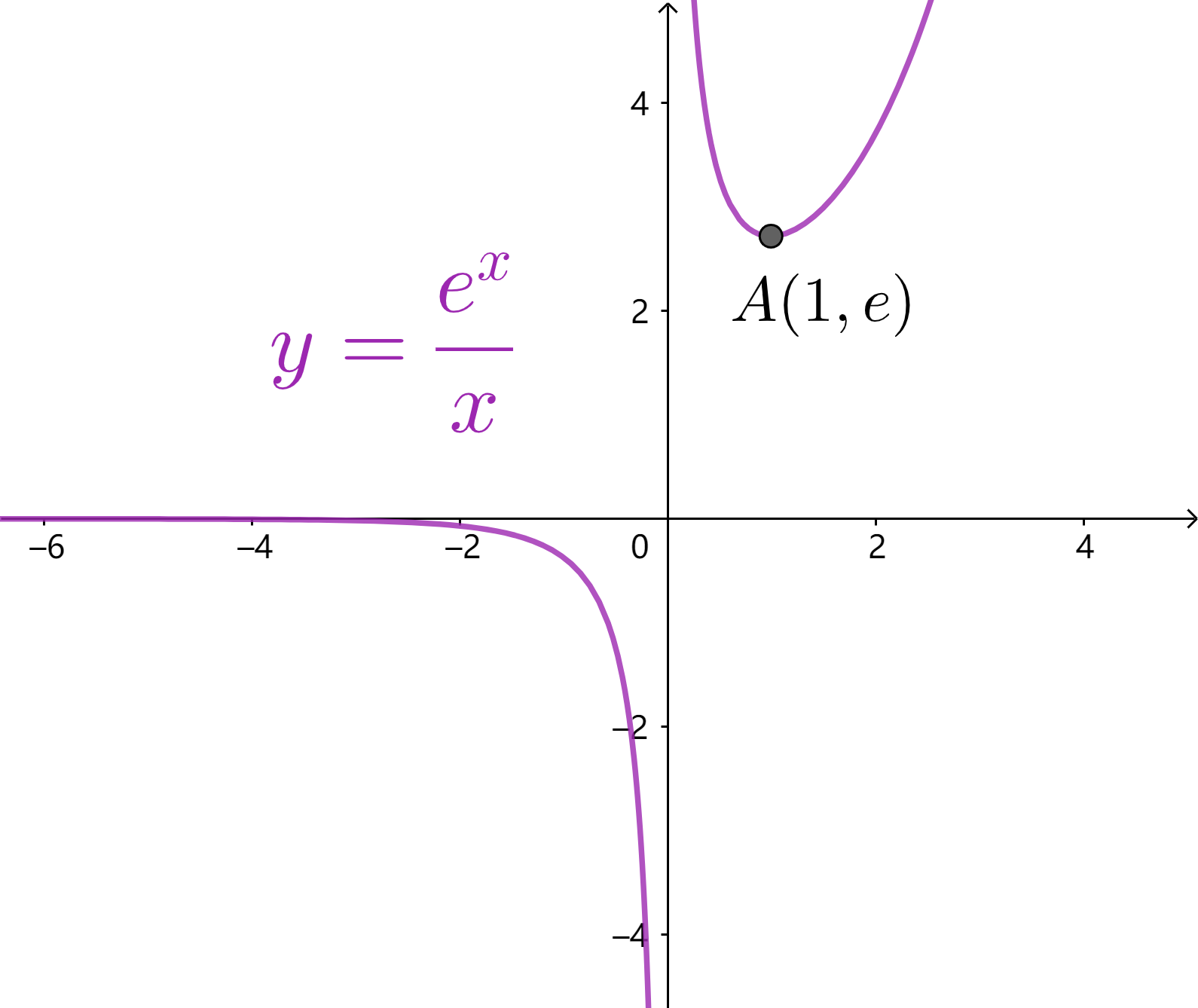
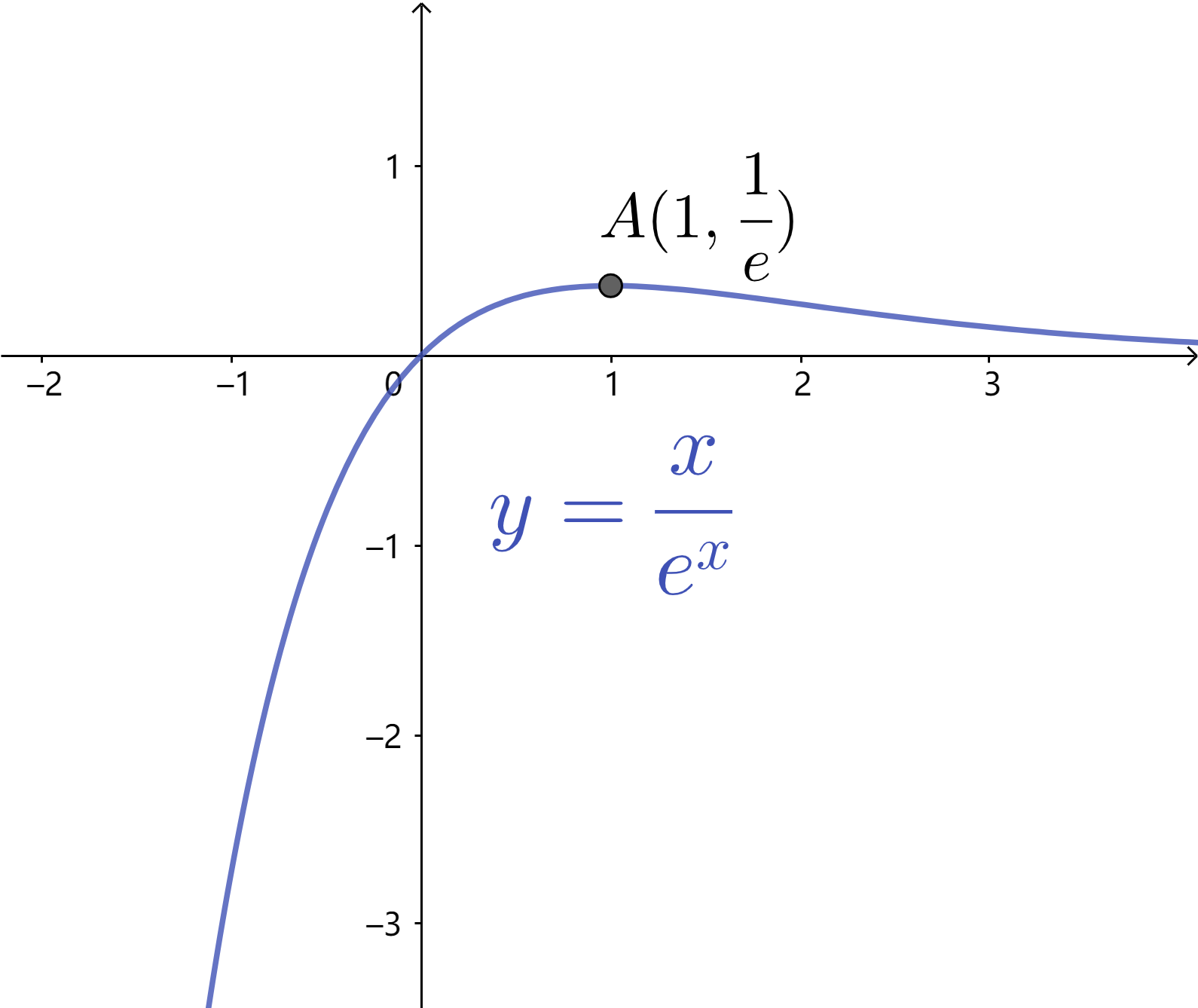
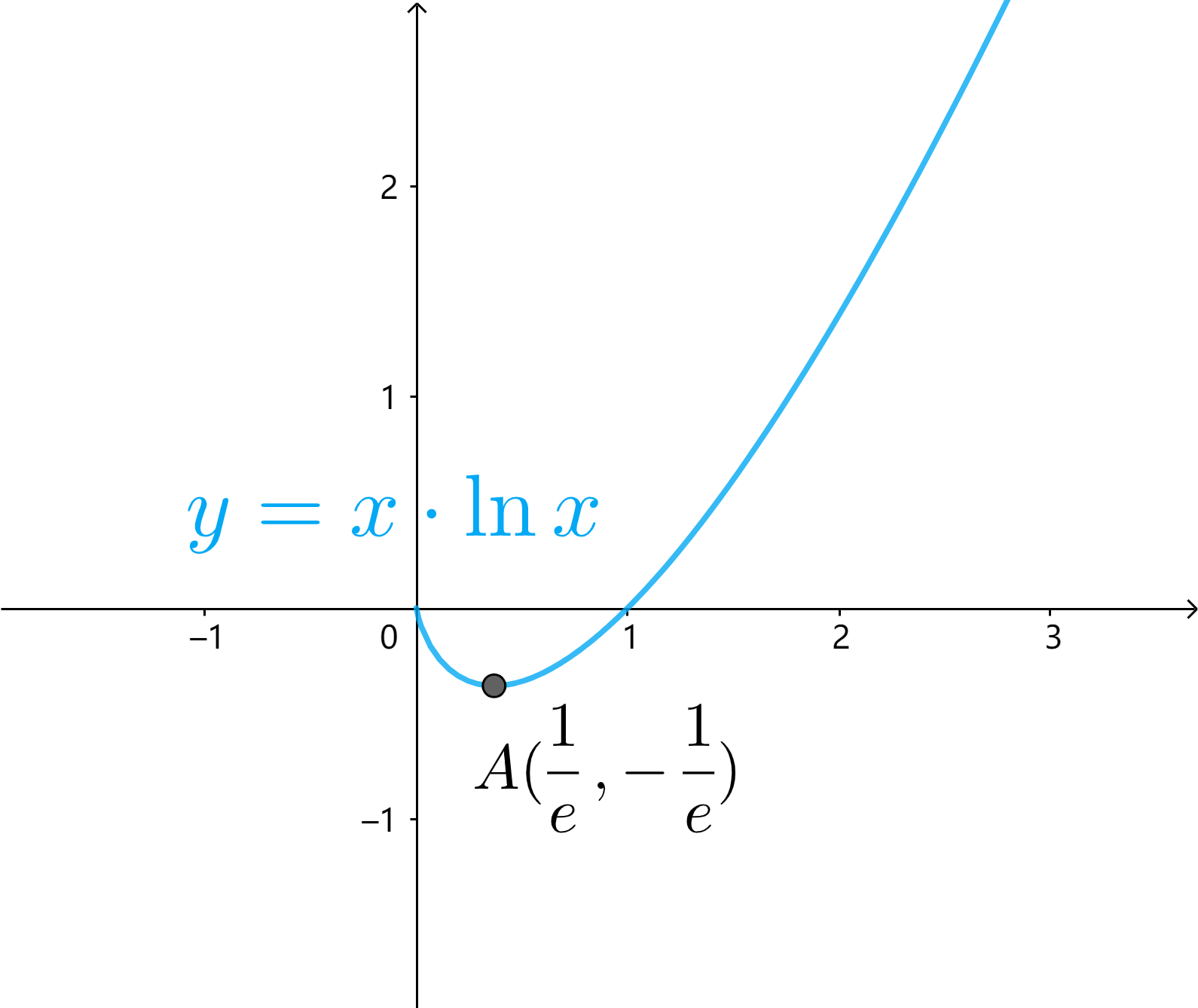
常用放缩不等式

• ★$\ln x<\frac{1}{2}(x-\frac{1}{x}),x>1$

• ★$\ln x>\frac{1}{2}(x-\frac{1}{x}),0<x<1$

• $\ln x<\sqrt{x}-\frac{1}{\sqrt{x}},x>1$

• $\ln x>\sqrt{x}-\frac{1}{\sqrt{x}},0<x<1$

• $\ln x\le -\frac{1}{2}(x-1)(x-3),0<x<1$

• $\ln x\ge -\frac{1}{2}(x-1)(x-3),x>1$

• ★$\ln x\ge 1-\frac{1}{x}$

• ★$\ln x>\frac{2(x-1)}{x+1},x>1$

• ★$\ln x<\frac{2(x-1)}{x+1},0<x<1$

• $x\ln x\ge x-1$

• $\ln x\le\frac{x}{e}$

• ★$e^x\ge x+1[+\frac{1}{2}x^2][+\frac{1}{6}x^3]$

• $e^x\ge x^2+1,x\ge 0$

• $e^{x-1}\ge \frac{x^2+1}{2},x\ge 0$

• ★$e^x\le\frac{1}{1-x},x<1$

• ★$e^x\ge\frac{1}{1-x},x>1$

• ★$e^x\ge ex$

• $e^x\ge ex+(x-1)^2,x\ge 0$

• $e^x\ge\frac{23}{15}x^2+1,x\ge 0$

• $\frac{e^x}{x}-x\ln x>2$

• $e^x\ge 2x+1-\ln(x+1)$

• $e^x>\ln(x+2)$

• 当 $0<x<1$ 时

  $\frac{x^2-1}{x^2+1}>\frac{2(x-1)}{x+1}>\frac{4(\sqrt{x}-1)}{\sqrt{x}+1}>\ln x$

• 当 $x>1$ 时

  $\frac{x^2-1}{x^2+1}<\frac{2(x-1)}{x+1}<\frac{4(\sqrt{x}-1)}{\sqrt{x}+1}<\ln x$

帕德逼近

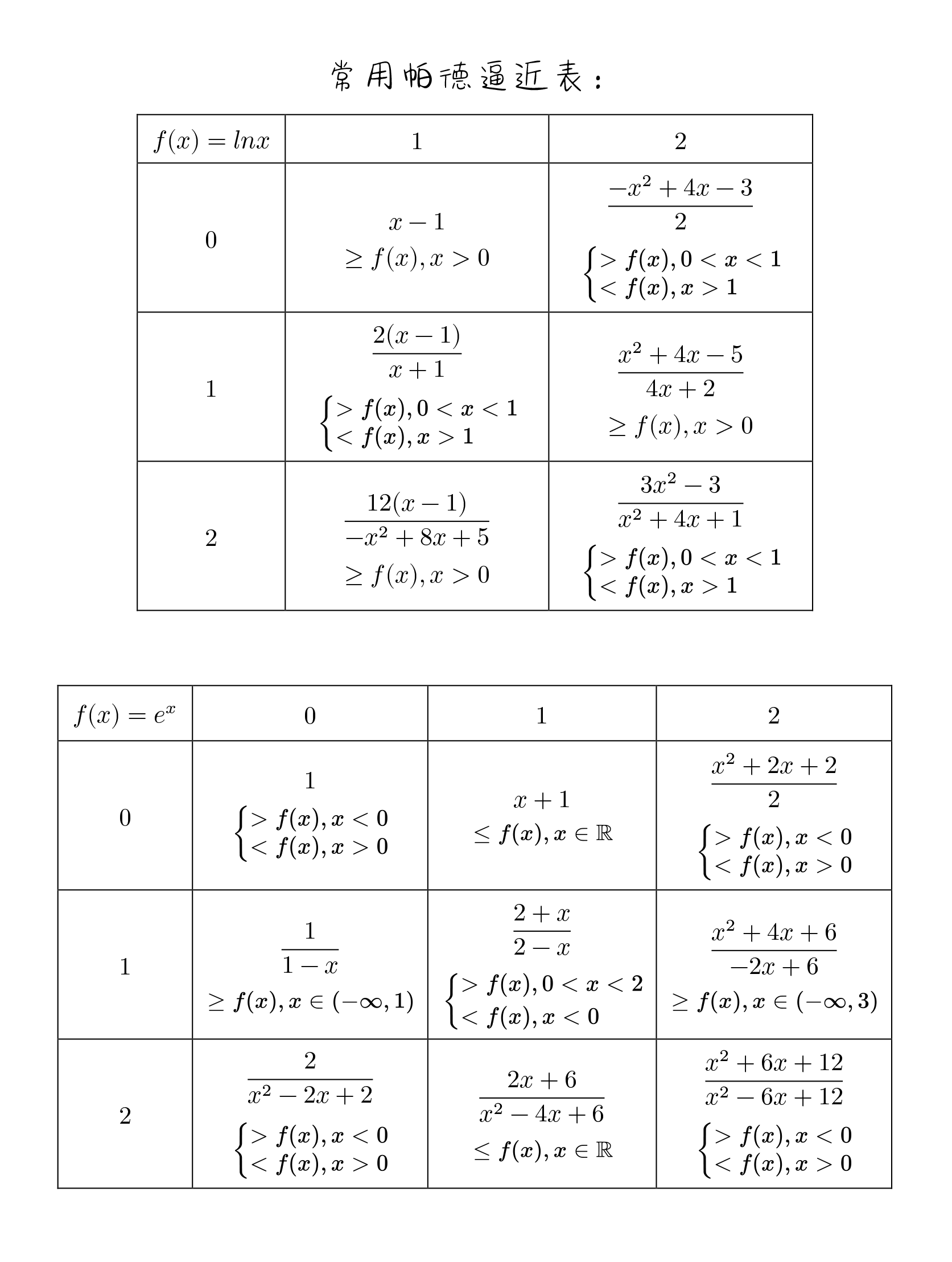
均值不等式加强版

幂平均数

$$\begin{array}{c} M_p(a,b)=(\frac{a^p+b^p}{2})^{\frac{1}{p}}\\ 若x\le y，则M_x\le M_y \end{array}$$

对数平均数

$$L(a,b)=\frac{b-a}{\ln b-\ln a}$$

指数平均数

$$\begin{array}{c} I(a,b)=\frac{1}{e}(\frac{b^b}{a^a})^{\frac{1}{b-a}}\\ \ln(I(a,b))=-1+\frac{b\ln b-a\ln a}{b-a} \end{array}$$

调和平均数

$$M_{-1}(a,b)=\frac{2}{\frac{1}{a}+\frac{1}{b}}$$

几何平均数

$$M_0(a,b)=G(a,b)=\sqrt{ab}$$

算数平均数

$$M_1(a,b)=A(a,b)=\frac{a+b}{2}$$

平方平均数

$$M_2(a,b)=\sqrt{\frac{a^2+b^2}{2}}$$

均值不等式

$$M_{-1}(a,b)\le M_0(a,b)=G(a,b)\le L(a,b)\le M_{\frac{1}{3}}(a,b)\le M_{\frac{1}{2}}(a,b)\le I(a,b)\le M_1(a,b)=A(a,b)\le M_2(a,b)$$

八、其他资料分享

50条高考数学秒杀公式方法，助你再提30分.pptx
解析几何中若干经典结论及其应用.docx