第一章 函数

1.描述集合中元素的方式：枚举法、属性法。

2.逻辑符号：略

3.数域的定义：设P是由一些复数组成的集合，其中包括0与1，如果P中任意两个数的和、差、积、商（除数不为0）仍是P中的数，则称P为一个数域。
扩展：“包括0与1”可以改成“包括0与x”

4.有理数有序的定义：

$$对于任意x,y\in \mathbb{Q}，x<y,x=y,x>y有且仅有一个成立$$

5.有理数集可数的定义：

$$\mathbb{Q}与自然数集\mathbb{N}能建立双射。$$

6.有理数稠密性的定义：

$$\forall a,b\in \mathbb{Q},a<b,\exists c \in \mathbb{Q},使得a<c<b$$

7.无理数也是稠密的

8.实数的连续性（完备性）：
实数与数轴上的点一一对应
或者
任意两个实数“中间”的数都是实数

9.[去心]领域的定义：略

10.ALG不等式、CS不等式：略

11.伯努利不等式：设实数$x>-1$，$a\ge 1$，则$(1+x)^a\ge 1+ax$

12.求证：$\sqrt[n]{n}-1<\frac{2}{\sqrt{n}}$

$$\begin{align} &\Leftrightarrow \sqrt[n]{n}-1<\frac{2\sqrt{n}}{n} \\ &\Leftrightarrow \sqrt[n]{n}<\frac{2\sqrt{n}}{n}+1 \\ &\Leftarrow \sqrt[n]{\sqrt{n}\cdot\sqrt{n}\cdot 1 \cdots 1}\text{(n-2个1)}\le\frac{2\sqrt{n}+n-2}{n}<\frac{2\sqrt{n}}{n}+1,n\ge 2 \end{align}$$

或者
构造$a_1=a_2=\sqrt{n},a_3=\cdots=a_n=1$，由AG不等式导出

13.求证：$(1+\frac{1}{n})^n\le(1+\frac{1}{n+1})^{n+1}$
构造$a_1=a_2=a_3=\cdots=a_n=1+\frac{1}{n},a_{n+1}=1$，由AG不等式导出

14.求证：$(1+\frac{1}{n})^{n+1}\ge(1+\frac{1}{n+1})^{n+2}$
构造$a_1=a_2=a_3=\cdots=a_{n+1}=1-\frac{1}{n+1},a_{n+2}=1$，由AG不等式导出

15.数集的界：
对非空实数集 $E\subset\mathbb{R} $，
（1）若$\exists M\in \mathbb{R}$，使得$\forall x \in E$，有$x\le M$，则称$M$是$E$的一个上界
（2）若$\exists m\in \mathbb{R}$，使得$\forall x \in E$，有$x\ge m$，则称$M$是$E$的一个下界
（3）若$\forall M>0,\exists x \in E:|x|>M$，则称数集$E$无界

16.数集的上下确界：
对非空实数集 $E\subset\mathbb{R} $，若$\exists \beta\in\mathbb{R}$满足：
（1）$\forall x\in E$，有$x\le \beta$；
（2）$\forall \varepsilon>0,\exists x_{\varepsilon}\in E$，使得$x_{\varepsilon}>\beta-\varepsilon$，
则称$\beta$是$E$的上确界，记为$\beta=\text{sup} \ E$

对非空实数集 $E\subset\mathbb{R} $，若$\exists \beta\in\mathbb{R}$满足：
（1）$\forall x\in E$，有$x\ge \beta$；
（2）$\forall \varepsilon>0,\exists x_{\varepsilon}\in E$，使得$x_{\varepsilon}<\beta+\varepsilon$，
则称$\beta$是$E$的下确界，记为$\beta=\text{inf} \ E$

17.数集中若有最大（小）值，则这个值是数集的上（下）确界。

18.确界存在性定理：
若非空数集E有上（下）界，则E必有上（下）确界。

19.单射、满射的定义：略

20.取整函数的性质：
（1）$x-1<[x]\le x<[x]+1$
（2）$[x+n]=[x]+n$

21.符号函数：略

22.狄利克雷(Dirichlet)函数：

$$D(x)=\left\{ \begin{aligned} 1 & ,x\in \mathbb{Q} \\ 0 & ,x\in \mathbb{Q}^c \end{aligned} \right.$$

$D_f=\mathbb{R},R_f={0,1}$

23.定义在$[0,1]$上的黎曼(Riemann)函数：

$$R(x)=\left\{ \begin{aligned} 1 & ,x=0,1 \\ \frac{1}{q} & ,x=\frac{p}{q}（p,q互质,p<q） \\ 0 & ,x\in \mathbb{Q}^c \end{aligned} \right.$$

24.函数的四则运算：略

25.函数的复合：
$(g○f)(x)\overset{\Delta}{=}g(f(x))$
条件：$R_f\cap D_g\ne \emptyset$

26.反函数：
条件：一一映射
$y=f(x)\longrightarrow x=f^{-1}(y)$

27.函数有界的定义：
设函数$f$的定义域为$I$
（1）若$\exists M \in \mathbb{R},\forall x \in I$，都有$f(x)\le M$，则称$M$为$f$的一个上界
（2）若$\exists m \in \mathbb{R},\forall x \in I$，都有$f(x)\ge m$，则称$m$为$f$的一个下界

28.初等函数：
由基本初等函数（常值函数，对数函数，幂函数，指数函数，三角及反三角函数）经过有限次四则运算与复合运算所得到的函数统称为初等函数。

29.函数的基本性质：略
双曲函数的性质：https://zhuanlan.zhihu.com/p/20042215
反三角函数的性质：https://www.zhihu.com/question/295227701

30.极坐标方程：
好难啊！这个我不会！

第二章 极限与连续

1.单调数列的定义：略

2.数列有界的定义：
$\exists M>0,\forall n \in \mathbb{N}^{+}:|x_n|\le M$
否命题的正面描述
$\forall M>0,\exists n \in \mathbb{N}^{+}:|x_n|> M$

3.数列极限的定义：
4.对数列${x_n}$，若

$$\exists A \in \mathbb{R},\forall \varepsilon>0,\exists N\in \mathbb{N}^{+},\forall n>N:|x_n-a|<\varepsilon,$$

则称数列${x_n}$收敛于$A$，记为$\lim_{n \to \infty} x_n=A$或$x_n\to A(n\to \infty)$
若不存在这样的$A$，则称数列${x_n}$无极限，也称数列${x_n}$发散或不收敛

5.数列极限$\lim_{n \to \infty} x_n=A$的等价定义：
（1）$\forall \varepsilon\in (0,1),\exists N\in \mathbb{N}^{+},\forall n>N:|x_n-A|<\varepsilon$

（2）$\forall \varepsilon>0,\exists N\in \mathbb{N}^{+},\forall n>N:|x_n-A|<m\varepsilon$,

$\left(m>0 \text{为常数}\right)$

（3）$\forall \varepsilon>0,{x_m}中最多只有有限项在A的\varepsilon邻域之内$

6.压缩映像原理：
设$\exists a \in \mathbb{R},\forall n \in \mathbb{N}$，有

$$|x_{n+1}-a|\le q|x_n-a|,\qquad (0<q<1)$$

则$\lim_{n \to \infty} x_n=A$

证明：

$$0<|x_{n+1}-a|\le q|x_n-a|\le \cdots \le q^n|x_1-a|$$ $$q^n无穷小量，|x_1-a|有界量，夹逼可得$$

7.无穷小量的定义：略

8.有限个无穷小的和/积是无穷小
无限个无穷小的和/积不一定是无穷小
例子：

$$\begin{array}{c} a_{m,n}=n-m\\ 对于任意i\in \mathbb{N}^{*}，\{a_{i,n}\}在n\to \inf为正无穷大\\ 但：\sum_{i=1}^{+\infty} a_{i,n}=-\infty,\forall n\in\mathbb{N}^{*} \end{array}$$

9.无穷小量乘以有界量仍为无穷小量

10.无穷小量一定有界

11.无穷大量的定义：
若$\forall M>0,\exists N \in \mathbb{N}^{+},\forall n >N:|x_n|>M$，
则称数列${x_n}$为无穷大量，记作$\lim_{n \to \infty} x_n=\infty$

若将$|x_n|>M$改为$x_n>M$，则称数列${x_n}$为正无穷大量，记作$\lim_{n \to \infty} x_n=+\infty$

若将$|x_n|>M$改为$x_n<-M$，则称数列${x_n}$为负无穷大量，记作$\lim_{n \to \infty} x_n=-\infty$

12.无穷大的倒数为无穷小

13.无穷大量一定无界，反过来不成立
事实上，数列无界的充要条件是数列存在子列为无穷大。

14.正无穷大量的相反数是负无穷大量

15.有限个无穷大的和/积是无穷大
无限个无穷大的和/积不一定是无穷大
有界量（即使非零）乘无穷大不一定是无穷大

16.数列极限的唯一性：略

17.收敛数列的有界性：略

18.减少（增加）数列的有限项，收敛性不变。

19.保号性：
若$\lim_{n \to \infty} x_n=A$，且$A>0$，则$\exists N \in \mathbb{N},\forall n>N:x_n>0$

20.保序性：
暂略

21.归并性：
$\lim_{n \to \infty} x_n=A$的充分必要条件是${x_n}$的任一子列${x_{n_k}}$均满足$\lim_{k \to \infty} x_{n_k}=A$
（A可以是无穷）

推论：
（1）$\lim_{n \to \infty} x_n=A$的充分必要条件是$\lim_{k \to \infty} x_{2k+1}=A$且$\lim_{k \to \infty} x_{2k}=A$
（2）更一般地，如果存在有限个子列，能取遍数列的所有元素，而这有限个子列均收敛于同一极限则该数列收敛。
（3）若数列有两个子列极限不同，或存在发散的子列，则该数列一定发散。
（4）单调数列${x_n}$收敛(于A) $\Leftrightarrow$ 存在一个收敛子列(收敛于A)
（5）数列无界的充要条件：存在一个子列为无穷大
（6）数列无上（下）界的充要条件：存在一个子列为正（负）无穷大

22.收敛数列极限的四则运算法则：略
推论：若$\lim_{n \to \infty} x_n=A$，$k$是正整数，则$\lim_{n \to \infty} x_n^k=A^k$

23.若$\lim_{n \to \infty} x_n=A$，$k$是正整数，则$\lim_{n \to \infty} x_n^k=A^k$

24.夹逼定理：
设$\lim_{n \to \infty} y_n=\lim_{n \to \infty} z_n=a$，
且$\exists N_0\in\mathbb{N},\forall n>N_0:y_n\le x_n\le z_n$，
则$\lim_{n \to \infty} x_n=a$
证明略

25.求证：$\lim_{n \to \infty} \sqrt[n]{n}=1$
证明：设$x_n=\sqrt[n]{n}-1$，则当$n\ge 2$时，

$$n=(1+x_n)^n=1+C_n^1x_n+C_n^2x_n^2+\cdots+x_n^n>\frac{n(n-1)}{2}x_n^2$$

从而有

$$0\le x_n<\sqrt{\frac{2}{n-1}}$$

由于$\lim_{n \to \infty}\sqrt{\frac{2}{n-1}}=0$，依夹逼定理得$\lim_{n \to \infty} x_n=0$，即

$$\lim_{n \to \infty} \sqrt[n]{n}=1$$

26.单调有界数列极限存在定理
若${x_n}$单调增加（减少）且有上界（下界），则${x_n}$收敛到其上（下）确界。
单调递增有上界，则$\lim_{n \rightarrow \infty} x_{n}=\sup_{n}{x_{n}}$
单调递减有下界，则$\lim_{n \rightarrow \infty} x_{n}=\inf_{n}{x_{n}}$
单调递增无上界，则$\lim_{n \rightarrow \infty} x_{n}=+\infty$
单调递减无下界，则$\lim_{n \rightarrow \infty} x_{n}=-\infty$

26.5.莱布尼茨判别法判断交错级数的收敛性
如果交错级数 $\sum_{n=1}^{\infty}(-1)^{n+1} u_{n}$ 满足以下两个条件：
(1) 数列 $\left\{u_{n}\right\}$ 单调递减
(2) $\lim_{n \rightarrow \infty} u_{n}=0$
那么该交错级数收敛，且其和满足 $S \leq u_{1}$。

27.求递推数列极限的方法：
（1）利用单调有界数列极限存在定理
a)证明有上界或下界
b)证明单调增或单调减
c)由“单调有界数列极限存在定理”知数列收敛，特征方程求极限
（2）用定义或压缩映像原理证明

28.闭区间套定理：
设闭区间列满足条件：
(1)$[a_{n+1},b_{n+1}]\subset [a_n,b_n],\forall n \in \mathbb{N}$
(2)$\lim_{n \rightarrow \infty}(b_n-a_n)=0$
则存在唯一$\xi\in[a_n,b_n] (\forall n \in \mathbb{N})$，使得$\lim_{n \to \infty} a_n=\lim_{n \to \infty} b_n=\xi$

29.函数极限的定义
总体而言：
从过程看，$x \rightarrow x_0$用$\delta$语言，$x \rightarrow \infty$用$X$语言;
从结果看，$f(x) \rightarrow A$用$\epsilon$语言，$f(x) \rightarrow \infty$用$M$语言(广义极限).

30.证明函数极限时记得保留$|x-a|$，并运用min、max对参数限制范围。

31.函数极限的无穷大、无穷小的定义

32.函数极限的唯一性：
若$\lim_{x \to a} f(x)=A$，又$\lim_{x \to a} f(x)=B$，那么$A=B$

33.函数极限的局部有界性：
若$\lim_{x \to a} f(x)=A$，则$\exists \epsilon>0$，使得函数$f(x)$在$a$的$\epsilon$去心邻域内有界

34.函数极限的局部保序性：
设$\lim_{x \to a} f(x)=A,\lim_{x \to a} g(x)=B$，且$A>B$，则$\exists \epsilon>0$，当$x$在$a$的$\epsilon$去心邻域内，$f(x)>g(x)$

35.函数极限的局部保号性：
若$\lim_{x\to a} f(x)=A,A>0(A<0)$，则$\exists \delta>0$，当$x\in \mathring{U}(a,\delta)$时，

$$f(x)>\frac{A}{2}>0\quad \left(f(x)<\frac{A}{2}<0\right)$$

推论：若$\exists \delta>0$，当$x\in \mathring{U}(a,\delta)$时，有$f(x)\ge 0 (f(x)\le 0)$，且$\lim_{x\to a} f(x)=A$，则

$$A\ge 0 \left(A\le 0\right)$$

36.函数极限的四则运算法则：略
$\lim_{x \rightarrow a}(f(x))^{\frac{k}{m}}=A^{\frac{k}{m}}$

37.复合函数的极限运算定理：
若$\lim_{u \to b} f(u)=A,\lim_{x \to a} \varphi(x)=b$，且当$x$在$a$的邻域内时，$\varphi(x)\ne b$，则

$$\lim_{x\to a} f[\varphi(x)]=A$$

38.夹逼定理
(1)$\exists \delta_{0}>0, \forall x \in \mathring{U}\left(x_{0}, \delta_{0}\right): g(x) \leqslant f(x) \leqslant h(x)$
(2)$\lim_{x \rightarrow x_{0}} g(x)=\lim_{x \rightarrow x_{0}} h(x)=A$
则必有$\lim_{x\to x_0} f(x)=A$

39.单调有界函数单侧极限的存在性

40.Heine归并定理
$\lim_{x\to a} f(x)=A$的充要条件为：对任一满足$\lim_{n \to \infty} x_n=a$且$x_n\ne a$的数列${x_n}$均有

$$\lim_{n \to \infty} f(x_n)=A$$

41.常用极限

• $\lim_{x\to 0}\frac{\sin{x}}{x}=\lim_{x\to 0}\frac{\tan{x}}{x}=1$
• $\lim_{x\to 0}\frac{1-\cos{x}}{x^2}=\frac{1}{2}$
• $\lim_{x\to 0}\frac{\ln(x+1)}{x}=\lim_{x\to 0}\frac{x}{e^x-1}=1$
• $\lim_{x \to 0} \frac{\arcsin x}{x}=\lim_{t \to 0} \frac{t}{\sin t}=1$
• $\lim_{x \to \infty}\left(1+\frac{1}{x}\right)^{x}=\lim_{x \to 0}(1+x)^{\frac{1}{x}}=e$
• $\lim_{n \to \infty} n(\sqrt[n]{a}-1)=\lim_{x \to 0} \frac{a^{x}-1}{x}=\lim_{t \to 0} \frac{t}{\frac{\ln (1+t)}{\ln a}}=\ln a\ (a>0)$
• $\lim_{x \to 0} \frac{(1+x)^{\alpha}-1}{x}=\alpha, \alpha \in \mathbb{R}$
• $\lim_{x\to a}\frac{\sin{x}-\sin{a}}{x-a}=\cos{a}$

42.幂指函数$f(x)^{g(x)}$的极限的计算

43.一个奇怪的技巧

$$\begin{align} &\lim_{x\to 0}\frac{\ln(1+x)-x}{x^2}\\ =&\lim_{x\to 0}\frac{\ln(1-x)+x}{x^2}\\ =&\lim_{x\to 0}\frac{\ln(1+x)-x}{2x^2}+\lim_{x\to 0}\frac{\ln(1-x)+x}{2x^2}\\ =&\lim_{x\to 0}\frac{\ln(1-x^2)}{2x^2}\\ =&-\frac{1}{2} \end{align}$$

44.无穷小的比较
设 $\lim_{x \rightarrow \Delta} f(x)=\lim_{x \rightarrow \Delta} g(x)=0, \lim_{x \rightarrow \Delta} \frac{f(x)}{g(x)}=l$
(1)若$l=0$，则称$x \rightarrow \Delta$时$\beta(x)$是比$\alpha(x)$高阶的无穷小，记为

$$\beta(x)=o(\alpha(x))\quad (x \rightarrow \Delta)$$

(2)若$l\ne 0$，则称$x \rightarrow \Delta$时$\beta(x)$是与$\alpha(x)$同阶的无穷小，记为

$$\beta(x)=O(\alpha(x))\quad (x \rightarrow \Delta)$$

特别地，若$l = 1$，则称$x \rightarrow \Delta$时$\beta(x)$是与$\alpha(x)$等价的无穷小，记为

$$\beta(x)\sim\alpha(x)\quad (x \rightarrow \Delta)$$

注：$f(x)=o(1)$表示$f(x)$在$x \rightarrow \Delta$时为无穷小

45.定义：若$\lim_{x \rightarrow a} f(x)=0$，且存在常数$c\ne 0,k>0:\lim_{x \rightarrow a} \frac{f(x)}{(x-a)^{k}}=c$，则称当$x \rightarrow a$时，$f(x)$是标准无穷小$x-a$的$k$阶无穷小，简称$f(x)$是阶无穷小，而称$c(x-a)^{k}$是$f(x)$的主部。

46.常见的等价无穷小

• $\sin{x}\sim\tan{x}\sim\ln(1+x)\sim e^x-1\sim\arcsin{x}\sim\arctan{x}\sim x$
• $1-\cos{x}\sim\frac{1}{2}x^2$
• $(1+x)^{\alpha}-1\sim\alpha x$
• $a^x-1\sim x\ln{a}$

47.等价无穷小替换的前提：
极限运算中，当分子分母的函数均有乘积项组成时，可对其中的乘积因子做无穷小替换。

48.函数间断点的定义
设函数$f(x)$在点$x_0$的某邻域内有定义，若

$$\lim_{x\to x_0}f(x)=f(x_0)$$

则称函数$f(x)$在$x_0$处连续，称$x_0$是$f(x)$的连续间断点；如果$f(x)$在$x_0$处不连续，则称$f(x)$在$x_0$处间断，称$x_0$是$f(x)$的间断点

简单来说，函数在某点连续就是在该点极限存在、值存在且两者相等

49.函数连续的定义：
设函数$f(x)$在点$x_0$的某右邻域内有定义，且

$$\lim_{x\to x_0^{+}}f(x)=f(x_0)$$

则称函数$f(x)$在$x_0$处右连续；
设函数$f(x)$在点$x_0$的某左邻域内有定义，且

$$\lim_{x\to x_0^{-}}f(x)=f(x_0)$$

则称函数$f(x)$在$x_0$处左连续。

或者说，函数 $f(x) $ 在 $x_{0}$ 点处连续是 指: $\forall \epsilon>0, \exists \delta>0, \forall x \in U\left(x_{0}, \delta\right): \mid f(x)- f\left(x_{0}\right) \mid<\epsilon$ , 即 $\lim_{x \rightarrow x_{0}} f(x)=f\left(x_{0}\right)$

• 若 $f(x)$ 连续，令 $f(x+\theta\Delta x)=f(x)+\alpha$,$\theta$ 是常数，则 $$\lim_{\Delta x\to 0}\alpha=0$$

例：黎曼函数在无理点连续，有理点不连续

$$R(x)=\left\{\begin{array}{ll} \frac{1}{p} & x \text { 为有理数 } \frac{q}{p}, p \in N^{+}, q \in Z \text { 且 } p 、 q \text { 互质 } \\ 1 & x=0 \\ 0 & x \text { 为无理数 } \end{array}\right.$$

50.定理：在点连续的充分必要条件是在点既左连续又右连续。
式子略

51.定义：若$f(x)$在区间$(a, b)$上的每一点都连续，则称$f(x)$在$(a,b)$上连续，记做$f\in C(a, b)$.

若$f(x)\in C(a,b)$，且$f(x)$在$x=a$处右连续，在$x=b$处左连续，则称$f(x)$在$[a,b]$上连续，记做$f\in C[a, b]$

52.复合函数的连续性定理
设$f(u)$在$u_0$处连续，$u = g(x)$在$x_0$处连续，$u_0= g(x_0)$。则复合函数$f(g(x))$在$x_0$处连续。

53.反函数连续性定理
设$f(x)$是区间$I$上严格单调的连续函数，则在$f(I)$上存在具有同样严格单调性的连续反函数$f^{-1}$。

54.初等函数的连续性
一切初等函数在其定义域上都是连续的

55.$f(x)$ 在 $ x_{0} $ 处间断是指下列三种情况之一：
(1)$f(x)$ 在 $ x_{0}$ 点处无定义；
(2)$\lim_{x \rightarrow x_{0}} f(x)$ 不存在；
(3)$\lim_{x \rightarrow x_{0}} f(x)$ 存在，但是不等于 $f(x_{0})$

56.间断点

• 第一类间断点：$\lim_{x\to x_0^{+}}f(x)$和$\lim_{x\to x_0^{-}}f(x)$均存在
• • 两者相等：可去间断点
• • 两者不相等：跳跃间断点
• 第二类间断点：$\lim_{x\to x_0^{+}}f(x)$和$\lim_{x\to x_0^{-}}f(x)$至少有一个不存在
• • 无穷间断点（不要求掌握）
• • 振荡间断点（不要求掌握）

57.连续函数的性质

• 定义在 $\mathbb{R}$ 上连续函数 $f(x)$ 的值域为 $(m,M)$，$-\infty,+\infty$ 处极限存在，则 $m,M$ 只能在 $-\infty,+\infty$ 处取到。

• 定义在 $(a,b)$ 上连续函数 $f(x)$ 的值域为 $(m,M)$，$x=a$ 和 $x=b$ 处极限存在，则 $m,M$ 只能在 $x=a$ 或 $x=b$ 处取到。

• 定义在 $\mathbb{R}$ 上连续函数 $f(x)$ 在开区间 $(a,b)$ 上的最值一定是极值。

  证明：
  设最值在 $x_0$ 处取到，$a < x_0 < b$，不妨设为最大值。
  由实数的稠密性，$\exists \delta >0,a<x_0-\delta<x_0<x_0+\delta<b$
  由最值的定义，$\forall x \in (a,b),f(x)\leqslant f(x_0)$
  所以 $\forall x \in (x_0-\delta,x_0+\delta),f(x)\leqslant f(x_0)$
  故 $x_0$ 为极大值点，$f(x_0)$ 为极大值。

• 定义在 $\mathbb{R}$ 上连续函数 $f(x)$，$\lim_{x\to \infty} f(x)=A$，则 $f(x)$ 存在最值。

  证明：
  由极限的定义，$\forall X>0,\exists \varepsilon>0,\forall |x|>X:|f(x)-A|<\varepsilon$
  于是，$\forall X>0$，若 $|x|>X$，则 $A-\varepsilon<f(x)<A+\varepsilon$；若 $|x|\leq X$，则根据“闭区间上连续函数有界”，$m\leq f(x) \leq M$
  所以 $f(x)$ 在 $\mathbb{R}$ 上连续有界

  下面反证，假设 $f(x)$ 不存在最值。因为 $f(x)$ 是连续函数，可设值域为 $(a,b)$
  易知 $a,b$ 只能在 $-\infty,+\infty$ 处取到。
  即 $a=b=A$，这与值域为 $(a,b)$ 矛盾，故假设不成立，$f(x)$ 存在最值

闭区间上连续函数的性质

57.有界性定理
设$f(x)\in C[a,b]$，则$f(x)$在$[a,b]$上有界。
证明：

58.最值定理
设$f(x) \in C[a, b]$ ，则$\exists x_{1}, x_{2} \in [a, b] :$ $f(x_{1})=\max_{x \in[a, b]}{f(x)},$ $f\left(x_{2}\right)=\min_{x \in[a, b]}{f(x)}$

59.零点存在性定理
设 $f(x) \in C[a, b]$ , 若 $f(a) \cdot f(b)<0$ , 则 $\exists \xi \in(a, b): f(\xi)=0$ .

60.介值性定理
设 $f(x) \in C[a, b]$, $M= \max_{x \in[a, b]}{f(x)}$, $m=\min_{x \in[a, b]}{f(x)}$，则$\forall \lambda \in[m, M]$,$\exists \xi \in[a, b]:$$ f(\xi)=\lambda$

易错分析

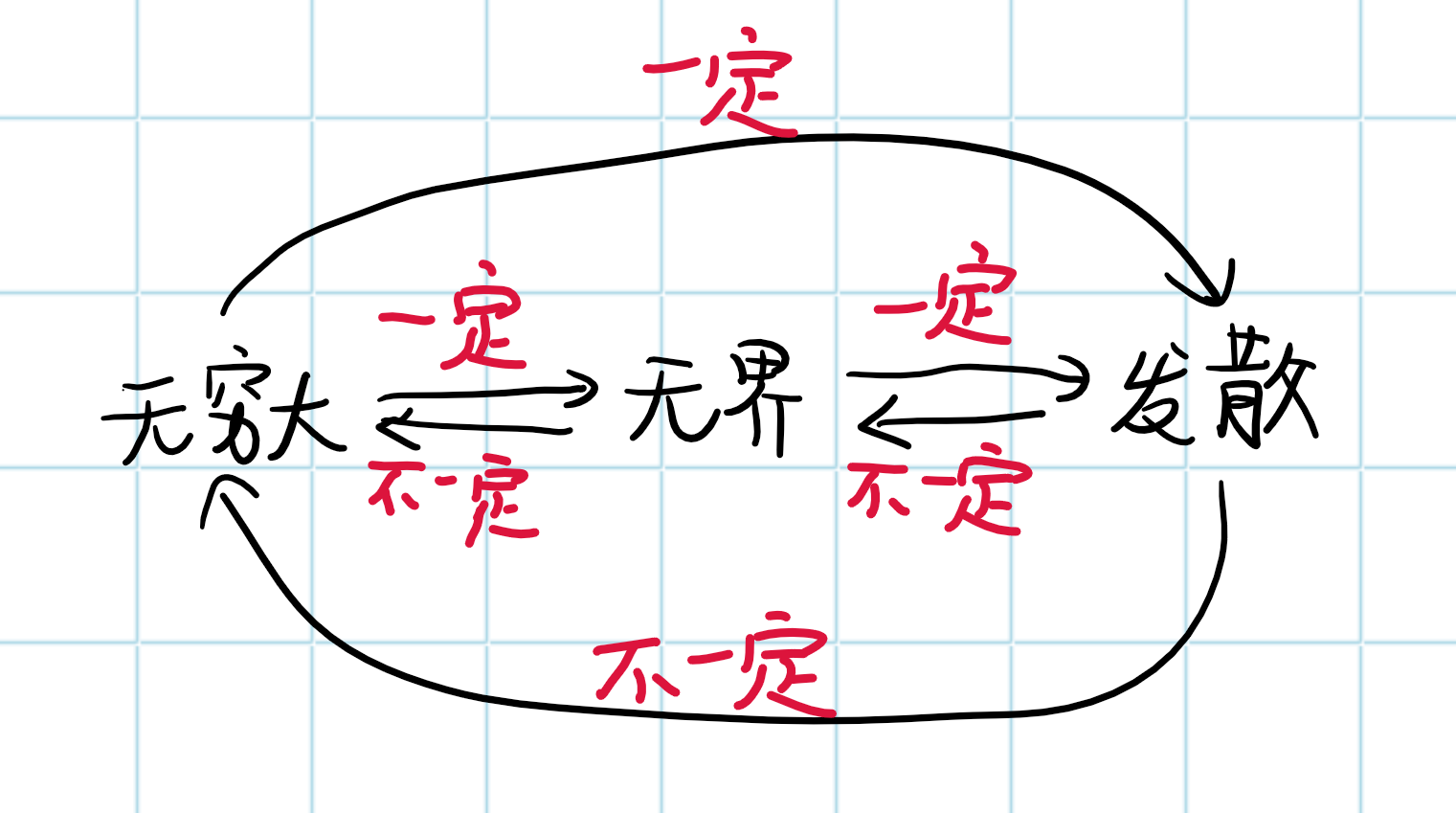
• 数列发散的定义： $$\forall A,\exists\varepsilon_0>0,\forall N \in \mathbb{N}^{*},\exists n>N:|x_n-A|\ge\varepsilon_0$$
• 数列无界的定义： $$\forall A>0,\exists n \in \mathbb{N}^{*}:|x_n|>A$$

• 数列无穷大的定义

  $$\forall G>0,\exists N\in \mathbb{N}^{*},\forall n>N:|x_n|>G$$

• 相互关系：
  

第三章 导数与微分

1.导数的定义：

2.单侧导数：
$f(x)$ 在 $x_{0}$处的左(右)导数, 记为 $f_{-}^{\prime}\left(x_{0}\right)\left(f_{+}^{\prime}\left(x_{0}\right)\right)$，函数的左、右导数统称为单侧导数。

3.函数可导的条件
设$f(x)$在$x_{0}$点处某邻域有定义，则$f\left(x_{0}\right)$在$x_{0}$点处可导的充要条件是$f_{-}^{\prime}\left(x_{0}\right)=f_{+}^{\prime}\left(x_{0}\right)$

4.注意单侧导数与导数单侧极限两个概念的区别

• 单侧导数存在，导数单侧极限不一定存在
  例:f(x)=0 当x＝0
  f(x)=x²sin(1/x) 当x≠0
  (以下只讨论导数右极限与右导数，左侧读者自行证明)
  在点0处 右导数:xsin(1/x) 其中x→0+，数值为0
  导数右极限:2xsin(1/x)+x²cos(1/x)(-1/x²)=-cos(1/x)其中x→0+ 不存在
• 导数单侧极限存在，单侧导数不一定存在
  例:f(x)=100 当x=0
  f(x)=x 当x≠0
  导数右极限为1 (x→0+)
  右导数:(x-100)/x 其中x→0+ 不存在

5.可导性和连续性

6.常见函数导数

$$\left(\frac{\sin x}{1+\cos x}\right)'=\frac{1}{1+\cos x}$$ $$\left(\frac{\cos x}{1+\sin x}\right)'=\frac{1}{1+\sin x}$$

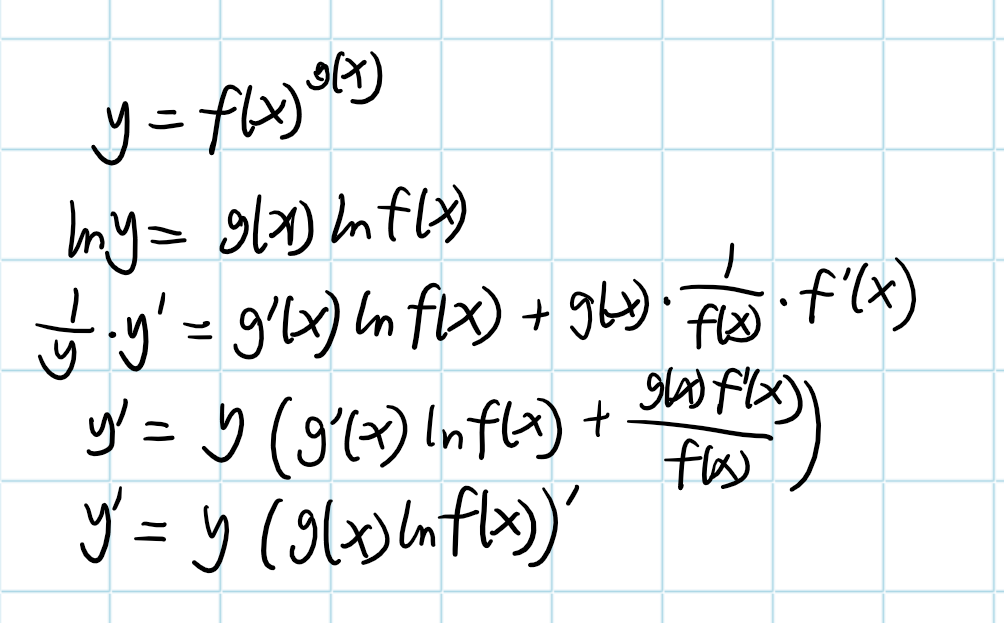
7.单侧导数的定义：$f(x)$在$x_0$处的左(右)导数，记为$f_{-}^{\prime}\left(x_{0}\right)\left(f_{+}^{\prime}\left(x_{0}\right)\right)$.函数的左、右导数统称为单侧导数。

• 设$f(x)$在$x_0$点处某邻域有定义，则$f(x)$在$x_0$点处可导的充要条件是$f_{-}^{\prime}\left(x_{0}\right)=f_{+}^{\prime}\left(x_{0}\right)$

8.函数在点$x_0$的单侧导数和导函数在该点的单侧极限是两个不同的概念

9.微分、可微、线性主部的定义：略

10.微分与导数的关系：$d y=f^{\prime}(x) \mathrm{d} x$

11.导数的四则运算：略

12.链式法则：

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\cdot\frac{\mathrm{d}u}{\mathrm{d}x}$$

13.反函数求导：设函数$y= f(x)$在$x_0$的某邻域内严格单调，连续，在$x_0$点处可导且$f^{\prime}\left(x_{0}\right) \neq 0$，则$f(x)$的反函数$x=\phi(y)$在点$y_0(y_0=f(x_0))$处可导，且有

$$\phi^{\prime}\left(y_{0}\right)=\frac{1}{f^{\prime}\left(x_{0}\right)}$$

14.高阶导数的概念：略

15.$n$阶连续可导：若$f^{(n)}$在$I$上连续，则称$f(x)$在$I$上$n$阶连续可导，记为$f(x) \in C^{(n)}(I)$

16.几个常用的基本初等函数的n次导数公式

• $\left[(a x+b)^{\alpha}\right]^{(n)}=\frac{\alpha!}{(\alpha-n)!} a^{n}(a x+b)^{\alpha-n}(n \in \mathbb{N}, a \neq 0)$
• $(\sin a x)^{(n)}=a^{n} \sin \left(a x+\frac{n \pi}{2}\right), n \in \mathbb{N}$
• $(\cos a x)^{(n)}=a^{n} \cos \left(a x+\frac{n \pi}{2}\right), n \in \mathbb{N}$
• $\left(a^{x}\right)^{(n)}=a^{x}(\ln a)^{n},(a>0)$
• $(\ln x)^{(n)}=(-1)^{n-1} \frac{(n-1) !}{x^{n}}$

17.设函数

$$f(x)=\left\{\begin{array}{lc} |x|^{\alpha} \sin \frac{1}{x}, \quad x \neq 0 \\ 0, \quad x=0 \end{array}\right.$$ $$\begin{matrix} & x=0处连续 & x=0处可导 & x=0处导数连续 & x=0处导数可导\\ \alpha\le 0 & × & × & N/A & N/A\\ 0<\alpha\le 1 & √ & × & N/A & N/A\\ 1<\alpha\le 2 & √ & √ & × & ×\\ 2<\alpha\le 3 & √ & √ & √ & ×\\ \alpha>3 & √ & √ & √ & √\\ \end{matrix}$$

18.莱布尼茨公式：

$$[u(x) v(x)]^{(n)}=\sum_{k=0}^{n} C_{n}^{k} u^{(k)}(x) v^{(n-k)}(x)$$

第四章 微分中值定理与导数的应用

19.费马（Fermat）引理：
若函数$f(x)$在$x_0$点处可导，且$x_0$为$f(x)$的极值点，则$f’(x_0)=0$

• $f’(x)$的零点称为$f(x)$的驻点或稳定点
• 可导的极值点必为驻点，驻点未必是极值点
• 几何意义：可导的极值点处的切线平行于$x$轴
• 推论：若$f(x)$在$x_0$处可导，为$f(x)$在区间$I$上的最值点，且为$I$的内点，则$f’(x_0)=0$

用于证明 $\exists \xi : f’(\xi)=0$类的题

20.罗尔（Rolle）中值定理
设 $f(x) \in C[a, b] \cap D(a, b)$ 且 $ f(a)=f(b)$，则 $\exists \xi \in(a, b): f^{\prime}(\xi)=0$

• 推论：若 $f(x) \in C[a, b] \cap D(a, b)$，且在 $ (a, b)$内 $ f^{\prime}(x) \neq 0 $， 则 $ y=f(x)$ 在 $ [a, b]$ 上为单射，从而必存在反函数
• 推广1：设函数 $ f(x) \in C[a,+\infty) \cap D(a,+\infty)$, $a$ 为常数。又 $ \lim_{x \rightarrow+\infty} f(x)=f(a)$，则 $\exists \xi \in(a ,+\infty): f^{\prime}(\xi)=0$.
• 用于计算函数零点个数或证明$f^{\prime}(\xi)+g(\xi) f(\xi)=0$类的题
  1.化为$f^{\prime}(\xi)+g(\xi) f(\xi)=0$的形式
  2.构造$F(x)=f(x)e^{u(x)}$，则$F^{\prime}(x)=f^{\prime}(x)+u^{\prime}(x) f(x)$
  3.利用 $u^{\prime}(x)=g(x)$求 $u(x)$，然后代入
  4.找到$x_1,x_2$，使得$F(x_1)=F(x_2)=0$
  5.利用罗尔定理，得出结论

若出现了二阶导数，往往需要找$F(x)$的三个零点

21.拉格朗日（Lagrange）中值定理
设 $ f(x) \in C[a, b] \cap D(a, b)$，则 $\exists \xi \in(a, b): f^{\prime}(\xi)=\frac{f(b)-f(a)}{b-a}$

• 常见变形
  • $\exists \xi \in(a, b): f(b)-f(a)=f^{\prime}(\xi)(b-a)$
  • $\exists \theta \in(0,1):f(b)-f(a)=f^{\prime}(a+\theta(b-a)) \cdot(b-a)$（有限增量公式）
  • $\exists \theta \in(0,1):f\left(x_{0}+h\right)-f\left(x_{0}\right)=f^{\prime}\left(x_{0}+\theta h\right) \cdot h$
  • $\exists \xi \in(a, x): f(x)-f(a)=f^{\prime}\left(\xi_{x}\right)(x-a)$
• 推论1：区间$I$上函数$f(x)=C$(常数) $\Leftrightarrow f^{\prime}(x)=0, \forall x \in I$
• 推论2：$f(x), g(x) \in C(I)$, $f^{\prime}(x)=g^{\prime}(x), x \in I$ $\Leftrightarrow \exists C: f(x)=g(x)+C$, $\forall x \in I$

用于证明与$f’(x)$相关的等式、不等式（尤其是出现了很多相似式子相减）

扩展：用拉格朗日中值定理求复杂极限

可参考https://zhuanlan.zhihu.com/p/366733582

• 共性：
  • 1.存在两项相减因式且形式相同；
  • 2.随着$x$的变化，因式的两项越来越接近（$\xi$所在区间变小）
• 做法：
  • 1.用拉格朗日中值定理$f(b)-f(a)=f^{\prime}(\xi)(b-a)$，其中$\xi \in(a, b)$
  • 2.由夹逼得出$\xi \sim a$或$\xi \sim b$
  • 3.继续使用其他技巧解题

22.柯西（Cauchy）中值定理
设 $f(x), g(x) \in C[a, b] \cap D(a, b)$, $g^{\prime}(x) \neq 0, x \in(a, b)$ ，则$ \exists \xi \in(a, b):$ $\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime}(\xi)}{g^{\prime}(\xi)}$

用于证明看起来上下都求了导的式子

23.达布（Darboux）定理
设 $f(x) \in D[a, b]$ , 且 $f^{\prime}(a)<f^{\prime}(b)$ , 则 $\forall \lambda \in\left(f^{\prime}(a), f^{\prime}(b)\right)$, $\exists \xi \in (a, b): f^{\prime}(\xi)=\lambda$

24.导数极限定理：
设函数$f(x)$在$x_0$处连续，在$x_0$的某去心邻域可导，且$\lim_{x \rightarrow x_{0}} f^{\prime}(x)$存在，则$f(x)$在$x_0$处可导，且$f’(x_0)=\lim_{x \rightarrow x_{0}} f^{\prime}(x)$ （即导函数在$x_0$处连续)

25.导函数的连续性定理
设 $f(x) \in D(a, b)$，则 $ (a, b)$ 内的点要么是 $f^{\prime}(x)$ 的连续点，要么是 $f^{\prime}(x)$ 的第二类间断点

• 推论：存在第一类间断点的函数必然不是某个函数的导函数

26.洛必达（L’Hôpital，或者L’Hospital）法则
若 $\exists \delta>0:$ $f(x), g(x) \in D\left(x_{0}, x_{0}+\delta\right)$, $ g^{\prime}(x) \neq 0$, $\forall x \in\left(x_{0}, x_{0}+\delta\right)$，又$\lim_{x \rightarrow x_{0}^{+}} \frac{f^{\prime}(x)}{g^{\prime}(x)}=A$（$A$为有限数或$\infty$）
1.$\lim_{x \rightarrow x_{0}^{+}} f(x)=\lim_{x \rightarrow x_{0}^{+}} g(x)=0$,则$\lim_{x \rightarrow x_{0}^{+}} \frac{f(x)}{g(x)}=A$
2.$\lim_{x \rightarrow x_{0}^{+}} g(x)=\infty$,则$\lim_{x \rightarrow x_{0}^{+}} \frac{f(x)}{g(x)}=A$

实际运用中结合等价无穷小替换和换元

扩展：数列中的洛必达定理：斯托尔茨(O.Stolz)定理

定理1（$\frac{*}{\infty}$型）

设数列 $\{a_{n}\}$ 、 $\{b_{n}\}$ 满足:
(1) $\{b_{n}\}$ 严格单调递增
(2) $\lim _{n \rightarrow \infty} b_{n}=+\infty$

那么:

$$\lim _{n \rightarrow \infty} \frac{a_{n+1}}{b_{n+1}}=\lim _{n \rightarrow \infty} \frac{a_{n}}{b_{n}}=\lim _{n \rightarrow \infty} \frac{a_{n+1}-a_{n}}{b_{n+1}-b_{n}}=L$$

(其中$L$可为有限数,$+\infty,-\infty$,不能是$\infty$)

特例：

$$\lim _{n \rightarrow \infty} \frac{a_{n+1}}{n+k+1}=\lim _{n \rightarrow \infty} \frac{a_{n}}{n+k}=\lim _{n \rightarrow \infty}a_{n+1}-a_{n}=L$$

定理2（$\frac{0}{0}$型）

设数列 $\{a_{n}\}$ 、 $\{b_{n}\}$ 满足:
(1) $\{b_{n}\}$ 严格单调递增
(2) $\lim _{n \rightarrow \infty} b_{n}=0$
(2) $\lim _{n \rightarrow \infty} a_{n}=0$

那么:

$$\lim _{n \rightarrow \infty} \frac{a_{n+1}}{b_{n+1}}=\lim _{n \rightarrow \infty} \frac{a_{n}}{b_{n}}=\lim _{n \rightarrow \infty} \frac{a_{n+1}-a_{n}}{b_{n+1}-b_{n}}=L$$

(其中$L$可为有限数,$+\infty,-\infty$,不能是$\infty$)

week7感想

中值定理是反映函数与导数之间联系的重要定理，也是微积分学的理论基础，在许多方面它都有重要的作用，在进行一些公式推导与定理证明中都有很多应用。

　　本周我们主要学习了三大微分中值定理，并通过具体例题初步了解了如何构造函数来运用中值定理，从而得出要证的式子。构造一直被认为是反直觉的方法。波利亚·哲尔吉在《怎样解题》中提到：

这个方法虽然看上去很完美，没有任何瑕疵，
但究竟是怎么想出这个方法的呢？
我究竟该怎么做才能想出或发现方法呢？

　　比如，你有一道中值定理的题不会做，看到答案，上来就是构造函数，你也不禁要问：为什么是这样构造的？答案是怎么想到这样构造的？回答这两个问题，我们就需要对常用函数有深刻的了解，比如你看到$f(x)+f’(x)$，你脑子里立刻应该跳出$e^x$，因为$(f(x)e^x)’=(f(x)+f’(x))e^x$。然后，通过不断重复记忆，增强前后关联程度，你才能在结论和原函数可能的形式之间来去自如。

　　我们还学了心心念念的洛必达法则。明白了洛必达法则的适用前提和内在原理。之前很多极限的计算到此方便了很多。同时也留下一个悬念：洛必达和泰勒到底谁更厉害呢？还要等下周再揭晓了

我一边想着那些计算公式，一边体会着古时候数学家们体验到的那份感动。即便是几百年前就已经被证明的也没关系，现在我一边追溯理论一边埋头苦思的东西一定是自己的东西。
——结城浩《数学女孩》

27.泰勒（Taylor）多项式
如果函数$f(x)$在点$x_{0}$处$n$阶可导, 则

$$p_{n}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}$$

• 泰勒系数
• 分时泰勒展开：
  x趋向于0，极限看上下多项式的最低次项；
  x趋向于$\infty$，极限看上下多项式的最高次项；

28.带皮亚诺（Peano）余项的泰勒公式
如果函数$f(x)$在点$x_0$的邻域内有定义，在点$x_0$处$n$阶可导，则

$$f(x)=\sum_{k=0}^{n} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k}+o\left(\left(x-x_{0}\right)^{n}\right)$$

• 展开式唯一
• 一般在$x\to x_0 $的情况下使用

29.麦克劳林（Mauclaurin）公式
当$x_0=0$时的泰勒公式

30.常见的麦克劳林展开

• $$\mathrm{e}^{x}=1+\frac{x}{1 !}+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n !}+\frac{\mathrm{e}^{\theta x}}{(n+1) !} x^{n+1}, \text { 其中 } \theta \in(0,1)$$
• $$\sin x=x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\cdots+(-1)^{n-1} \frac{x^{2 n-1}}{(2 n-1) !}+(-1)^{n} \frac{\cos \theta x}{(2 n+1) !} x^{2 n+1} \text {, 其中 } \theta \in(0,1)$$
• $$\cos x=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\cdots+(-1)^{n} \frac{x^{2 n}}{(2 n) !}+(-1)^{n+1} \frac{\cos \theta x}{(2 n+2) !} x^{2 n+2} \text {, 其中 } \theta \in(0,1)$$
• $$\ln (1+x)=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}-\cdots+(-1)^{n-1} \frac{1}{n} x^{n}+(-1)^{n} \frac{1}{(n+1)(1+\theta x)^{n+1}} x^{n+1} \text {, 其中 } \theta \in(0,1),x\in(-1,1]$$
• $$(1+x)^{\alpha}= 1+\alpha x+\frac{\alpha(\alpha-1)}{2 !} x^{2}+\cdots+\frac{\alpha(\alpha-1) \cdots(\alpha-n+1)}{n !} x^{n}+ \frac{1}{(n+1) !} \alpha(\alpha-1)(\alpha-2) \cdots(\alpha-n)(1+\theta x)^{\alpha-n-1} x^{n+1},|x|<1$$
• $$\frac{1}{1+x}=1-x+x^{2}+\cdots+(-1)^{n} x^{n}+\frac{(-1)^{n+1}}{(1+\theta x)^{n+2}} x^{n+1}, \text { 其中 } \theta \in(0,1),|x|<1$$
• $$\frac{1}{1-x}=1+x+x^{2}+\cdots+x^{n}+\frac{x^{n+1}}{(1-\theta x)^{n+2}},\text { 其中 } \theta \in(0,1),|x|<1$$
• $$\arctan x=x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-\cdots+\frac{(-1)^{n} x^{2 n+1}}{2 n+1}+o(x^{2n+2})$$

31.带拉格朗日（Lagrange）余项的泰勒公式
设$f(x)$在包$x_{0}$点的某开区间$(a, b)$内$n+1$阶可导，则$\forall x \in(a, b)$，有

$$f(x)=\sum_{k=0}^{n} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k}+\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right)^{n+1}$$

Toeplitz定理

若：
(1)$\forall n,k \in \mathbb{N}, t_{n,k} \geq 0$；
(2)$\forall n \in \mathbb{N},\sum_{k=1}^{n} t_{n,k}=1$；
(3)$\forall k \in \mathbb{N},\lim_{n \rightarrow \infty} t_{n,k}=0$；
(4)$\lim_{n \rightarrow \infty} a_{n}=A$
则有$\lim_{n \rightarrow \infty} \sum_{k=1}^{n} t_{n,k} a_{k}=A$

函数的性质

32.定理：设$f(x)\in C[a,b]\cap D(a, b)$，则$f(x)$在$[a,b]$上递增(或递减)的充要条件是$\forall x \in (a, b) :f’(x)\ge 0$

33.定理：设$f(x)\in C[a,b]\cap D(a, b)$，则$f(x)$在$[a,b]$上严格单调递增(或严格单调递减)
的充要条件是$\forall x \in (a, b) :f’(x)\ge 0$（或者$f’(x)\le 0$）,并且$(a,b)$内任意子区间上$f’(x)$不恒为$0$

34.Jordan不等式：当$x \in\left(0, \frac{\pi}{2}\right)$时，$\frac{2}{\pi}<\frac{\sin x}{x}<1$

35.极值第一判别法（充分性定理）
设函数$f(x)$在点$x_{0}$的某个邻域$U\left(x_{0}, \delta\right)$上连续，且在去心邻域$\mathring{U}\left(x_{0}, \delta\right)$内可导，
(1) 若在$x_{0}$左侧$f^{\prime}(x)<0$，在$x_{0}$右侧$f^{\prime}(x)>0$，则$x_{0}$是$f(x)$的极小值点；
(2) 若在$x_{0}$左侧$f^{\prime}(x)>0$，在$x_{0}$右侧$f^{\prime}(x)<0$，则$x_{0}$是$f(x)$的极大值点；
(3) 若在$x_{0}$两侧$f^{\prime}(x)$同号, 则$x_{0}$不是$f(x)$的极值点

• 例： $$f(x)=\left\{\begin{array}{ll} -x^{2}\left(2+\sin \frac{1}{x}\right), & x \neq 0 \\ 0, & x=0 \end{array}\right.$$ $f(0)=0$为极大值, 在$x=0$两侧任意邻域都不单调。

36.极值第二判别法（充分性定理）
设$f(x)$在$x_0$处二阶可导，且$f’(x_0) =0$，
(1) 若$f’’(x_0)<0$，则$f(x_0)$为严格极大值；

(2) 若$f’’(x_0)>0$，则$f(x_0)$为严格极小值。

37.最值计算的一般步骡：
1)求导数$f’(x)$；
2)$f’(x)=0$，求出所有的驻点和不可导点；
3)比较$f(x)$所有驻点、不可导点及区间端点处（包括$\infty$）的函数值，确定该函数的最大值与最小值。

38.凸函数的定义：
设$f(x)$定义在区间$I$上。若$\forall x_{1}, x_{2} \in I, \forall\lambda \in(0,1)$都有$f\left(\lambda x_{1}+(1-\lambda) x_{2}\right) \leqslant \lambda f\left(x_{1}\right)+(1-\lambda) f\left(x_{2}\right)$，则称$f(x)$为$I$上的下凸函数。

• 上式中严格不等式成立，则称$f(x)$为$I$上的严格下凸函数。不等式反向，则称$f(x)$为$I$上的上凸函数，可类似定义严格上凸函数。

39.凸性的第一判别法：
设$f(x)\in D(a, b)$，若$f’(x)$在$(a,b)$内严格单调递增(递减),则$f(x)$在$(a,b)$内为严格下凸(上凸)函数。

40.凸性的第二判别法：
设$f(x)$在$(a, b)$内二阶可导, 则:

• $f^{\prime \prime}(x)>0$时,$f(x)$在$(a, b)$内为下凸函数;
• $f^{\prime \prime}(x)<0$时,$f(x)$在$(a, b)$内为上凸函数。

41.拐点的定义：
设函数$f(x)$在点$x_0$的某邻域$U(x_0)$内连续,而在$x_0$的左右两侧$f(x)$有不同的凸性，则称$x_0$为$f(x)$的拐点。

• 函数的拐点应落在二阶导数为0，或者二阶导数不存在的那些点上。

42.Young不等式：
设 $A, B \geqslant 0$,$ p, q>0 $, 且 $\frac{1}{p}+\frac{1}{q}=1 $, 则有

$$\sqrt[p]{A} \sqrt[q]{B} \leqslant \frac{A}{p}+\frac{B}{q}$$

43.渐近线定义：
设$C$为平面曲线$y= f(x)$。若存在直线$L$，当动点$P$沿曲线$C$无限远离原点时，点$P$与直线$L$的距离趋于$0$，则称直线$L$为曲线$C$的渐近线。
(1) 若存在常数$c: \lim_{x \rightarrow+\infty} f(x)=c $, 或 $\lim_{x \rightarrow-\infty} f(x)= c$ , 则称直线 $y=c$ 为曲线 $ C $ 的水平渐近线;
(2) 若存在常数$x_{0} : \lim_{x \rightarrow x_{0}^{+}} f(x)=\infty$ 或 $\lim_{x \rightarrow x_{0}^{-}} f(x)= \infty $, 则称直线 $x=x_{0}$ 为曲线 $C$的垂直渐近线; （此时 $x_{0}$ 为函数 $y=f(x)$ 的无穷间断点。)
(3) 若存在常数 $a, b : \lim_{x \rightarrow+\infty}(f(x)-(a x+b))=0$ 或 $\lim_{x \rightarrow-\infty}(f(x)-(a x+b))=0$ , 则称 $y=a x+b$ 为曲线 $C$ 的斜渐近线.

44.函数作图的一般步骤：
(1)确定定义域、零点(与x轴，y轴的交点)与间断点，考虑函数的奇偶性、周期性等；
(2)确定函数的单调区间与极值点、凸性区间与拐点；
(3)确定渐近线：水平渐近线（看x取$\pm\infty$的极限），垂直渐近线（看没定义的点），斜渐近线（求$k=\lim_{x \rightarrow\pm\infty} \frac{f(x)}{x}$与$b=\lim_{x \rightarrow\pm\infty}(f(x)-kx)$）；
(4)列表反映上述信息，由列表数据给出函数的单调性、凸性；间断点、驻点、拐点、不可导点为分区间的依据。
(5)作图。图上标注：极值点坐标，拐点坐标，渐近线方程。

45.求方程的近似解：二分法/牛顿切线法

第五章 积分

问题的提出

略

定义符号

$$\begin{array}{|l|l|} \hline T:[a, b] & \text { 对 }[a, b] \text { 的分划 } T: a=x_{0}<x_{1}<\cdots<x_{n}=b ; \\ \hline \Delta x_{k} & x_{k}-x_{k-1} \text { 小区间的长度 } \\ \hline\|T\| & \max _{1 \leqslant k \leqslant n}\left\{\Delta x_{k}\right\}, \text { 称为分划 } T \text { 的细度; } \\ \hline \xi(T) & \text { 分划 } T \text { 下的介点集 }\left\{\xi_{k} \mid \xi_{k} \in\left[x_{k-1}, x_{k}\right], k=1, \cdots n\right\} ; \\ \hline \sum_{k=1}^{n} f\left(\xi_{k}\right) \Delta x_{k} & \text { 称为Riemann 和 } \\ \hline \end{array}$$

可积的定义

设$f(x)$在$[a,b]$上有界。在$[a,b]$上的任意分划$T: [a,b]$，任取介点集$\xi(T)$，作Riemann和$\sum_{k=1}^{n} f\left(\xi_{k}\right) \Delta x_{k}$.当$|T|\to 0$时，若上述和式的极限存在，且此极限的存在性与分划T及相应的介点集$\xi(T)$的取法无关，则称$f(x)$在$[a,b]$上Riemann可积，简称可积，记作$f(x) \in R[a,b]$，并将该极限值称为函数$f(x)$在$[a,b]$上的定积分，记作$\int_{a}^{b} f(x)\mathrm{d}x$

可积的充分条件

设$f(x):[a, b] \rightarrow \mathbb{R} $满足下列条件之一，则$f(x) \in R[a, b]:$

• $f(x) \in C[a, b]$
• $f(x)$为$[a, b]$上只有有限个间断点的有界函数
• $f(x)$在$[a, b]$上单调有界

分段连续函数定义

若函数$f(x)$在区间$[a,b]$上除有限个第一类间断点外均连续，则称$f(x)$是$[a,b]$上的分段连续函数

定积分的基本性质

设$f(x),g(x)\in R[a,b]$，则

• 线性性： $$\int_{a}^{b} [\alpha f(x)+\beta g(x)]\mathrm{d}x=\alpha\int_{a}^{b}f(x)\mathrm{d}x+\beta\int_{a}^{b}g(x)\mathrm{d}x$$
• 保号性：若$f(x)\ge 0$在$[a,b]$上成立，则 $$\int_{a}^{b} f(x)\mathrm{d}x\ge 0$$
• 保序性：若$f(x)\le g(x)$在$[a,b]$上成立，则 $$\int_{a}^{b} f(x)\mathrm{d}x\le \int_{a}^{b} g(x)\mathrm{d}x$$
• 区间可加性： $$\int_{a}^{c} f(x)\mathrm{d}x=\int_{a}^{b} f(x)\mathrm{d}x+\int_{b}^{b} f(x)\mathrm{d}x$$
• 估值不等式：若$m\le f(x)\le M$在$[a,b]$上成立，则 $$m(b-a)\le \int_{a}^{b} f(x)\mathrm{d}x \le M(b-a)$$
• 绝对值不等式：若$|f(x)| \in R[a,b]$，则 $$\left|\int_{a}^{b} f(x)\mathrm{d}x\right| \le \int_{a}^{b} |f(x)|\mathrm{d}x$$
• 柯西（Cauchy·Schwarz）不等式： $$\left(\int_{a}^{b} f(x) g(x) \mathrm{d} x\right)^{2} \leqslant \int_{a}^{b} f^{2}(x) \mathrm{d} x \cdot \int_{a}^{b} g^{2}(x) \mathrm{d} x$$
• 乘积函数可积性： $$f(x)g(x) \in R[a,b]$$

积分第一中值定理

设 $f(x), g(x) \in R[a, b] $，且 $g(x)$ 在$[a, b]$上不变号。记 $M, m$分别为$f(x)$在$[a, b]$上的上、下确界，则$\exists \lambda \in[m, M]: $

$$\int_{a}^{b} f(x) g(x) \mathrm{d} x=\lambda \int_{a}^{b} g(x) \mathrm{d} x$$

• 推论：若$f(x) \in C[a, b]$,$g(x) \in R[a, b]$且不变号, 则$\exists \xi \in[a,b]:$ $$\int_{a}^{b} f(x) g(x) \mathrm{d} x=f(\xi) \int_{a}^{b} g(x)\mathrm{d} x$$
• 特别地，若$f(x) \in C[a, b]$，则$\exists\xi \in[a, b]:$ $$\int_{a}^{b} f(x) \mathrm{d} x=f(\xi)(b-a)$$
• $\frac{\int_{a}^{b} f(x) \mathrm{d} x}{b-a}$称为函数$f(x)$在$[a, b] $上的平均值

原函数的定义

设$f(x)$和$F(x)$是定义在区间$I$上的函数，如果对于$\forall x \in I$，都有$F’(x)= f(x)$，则称$F(x)$是$f(x)$在区间$I$上的一个原函数，可等价地表示为$\mathrm{d}(F(x))=f(x)\mathrm{d}x$，$F(x)+C$可以代表$f(x)$的全部原函数。

不定积分的定义

$f(x)$在$I$上的原函数的全体称为$f(x)$在$I$上的不定积分，记为$\int f(x) \mathrm{d} x$，其中$\int$称为积分号，$f(x)$称为被积函数，$x$称为积分变量，$\mathrm{d}$是微分算符。若$F(x)$是$f(x)$在$I$上的原函数，则$\int f(x) \mathrm{d} x = F(x)+C$，其中$C$为积分常数。

变限积分函数定义

如果$f(x) \in R[a, b]$，则$f(x)$的部分区间$[a, x]\subset[a, b]$上也可积，从而

$$\varphi(x)=\int_{a}^{x} f(t) \mathrm{d} t, x \in[a, b]$$

定义了一个$[a, b]$上的新函数，称为变上限积分或者积分上限函数。同样可以定义变下限积分

$$\psi(x)=\int_{x}^{b} f(t) \mathrm{d} t, x \in[a, b]$$

变限积分相关定理

记$\varphi(x)=\int_{a}^{x} f(t) \mathrm{d} t, t \in[a, b]$

• 若$f(x) \in R[a, b]$, 则$\varphi(x) \in C[a, b]$
• 若$f(x) \in C[a, b]$, 则$\varphi(x) \in D[a, b]$，且$\varphi^{\prime}(x)=f(x)$,$x \in[a, b]$，即$\frac{d}{\mathrm{d} x} \int_{a}^{x} f(t) \mathrm{d} t$=$\lim_{\Delta x \rightarrow 0} \frac{\int_{x}^{x+\Delta x} f(t) \mathrm{d} t}{\Delta x}$=$f(x)$
• $f(x)$可积，变限积分一定连续
• $f(x)$连续，变限积分一定可导（反过来不成立）

原函数存在定理

连续函数必定有原函数，变上限积分函数就是它的一个原函数。

变限积分函数求导

$$\left(\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(t) \mathrm{d} t\right)^{\prime}=f\left[\varphi_{2}(x)\right] \varphi_{2}^{\prime}(x)-f\left[\varphi_{1}(x)\right] \varphi_{1}^{\prime}(x)$$

注意： $f(t)$ 不能与 $x$ 相关！！！

牛顿-莱布尼兹(Newton-Leibnitz)公式

设$f(x) \in R[a, b]$,$F(x) \in C[a, b]$，且 $\forall x \in(a, b)$, $F^{\prime}(x)=f(x)$，则

$$\int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a) \overset{\Delta}{=} F(x)|_{a}^{b}$$

有原函数、函数可积、函数可导、函数有界、函数连续的关系

不定积分表

• $$\int x^{\alpha} \mathrm{d}x = \frac{1}{\alpha+1} x^{\alpha+1}+C, \quad \alpha \neq-1 \quad$$
• $$\int \frac{1}{x} \mathrm{d}x = \ln |x|+C$$
• $$\int a^{x} \mathrm{d}x = \frac{1}{\ln a} a^{x}+C, \quad a>0, a \neq 1 \quad$$
• $$\int e^{x} \mathrm{d}x = e^{x}+C$$
• $$\int \sin x \mathrm{d}x = -\cos x+C \quad$$
• $$\int \cos x \mathrm{d}x = \sin x+C$$
• $$\int \tan x \mathrm{d}x = -\ln |\cos x|+C$$
• $$\int \cot x \mathrm{d}x = \ln |\sin x|+C$$
• $$\int \sec x \mathrm{d}x = \ln |\sec x+\tan x|+C$$
• $$\int \csc x \mathrm{d}x = \ln |\csc x-\cot x|+C$$
• $$\int \sec ^{2} x \mathrm{d}x = \tan x+C$$
• $$\int \csc ^{2} x \mathrm{d}x = -\cot x+C$$
• $$\int x\cos x \mathrm{d}x = \cos x + x\sin x + C$$
• $$\int x\sin x \mathrm{d}x = \sin x - x\cos x + C$$
• $$\int \frac{1}{1+\cos x} \mathrm{d}x = \frac{\sin x}{1+\cos x} + C$$
• $$\int \frac{1}{1+\sin x} \mathrm{d}x = \frac{\cos x}{1+\sin x} + C$$
• $$\int \frac{1}{\sqrt{a^{2}-x^{2}}} \mathrm{d}x=\arcsin \frac{x}{a}+C$$
• $$\int \frac{1}{a^{2}+x^{2}} \mathrm{d}x=\frac{1}{a} \arctan \frac{x}{a}+C$$
• $$\int \frac{1}{x^{2}-a^{2}} \mathrm{d}x=\frac{1}{2 a} \ln \left|\frac{x-a}{x+a}\right|+C$$
• $$\int \frac{1}{\sqrt{x^{2} \pm a^{2}}} \mathrm{d}x=\ln |x+\sqrt{x^{2} \pm a^{2}}|+C$$
• $$\int \sqrt{a^{2}-x^{2}} \mathrm{d}x=\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \arcsin \frac{x}{a}+C$$
• $$\int \sqrt{x^{2} \pm a^{2}} \mathrm{d}x=\frac{x}{2} \sqrt{x^{2} \pm a^{2}} \pm \frac{a^{2}}{2} \ln |x+\sqrt{x^{2} \pm a^{2}}|+C$$
• $$\int \log _{a} x \mathrm{d}x =x \log _{a} x-x \log _{a} e+C$$
• $$\int \ln x \mathrm{d}x =x \ln x-x+C$$
• $$\int \arcsin x \mathrm{d}x = x \arcsin x+\sqrt{1-x^{2}}+C$$
• $$\int \arccos \mathrm{d}x = x \arccos x-\sqrt{1-x^{2}}+C$$
• $$\int \arctan x \mathrm{d}x = x \arctan x-\frac{1}{2} \ln \left(1+x^{2}\right)+C$$
• $$\int \operatorname{arccot} x \mathrm{d}x = x \operatorname{arccot} x+\frac{1}{2} \ln \left(1+x^{2}\right)+C$$

• $\tan^{n}(x)$
  

第一换元积分法（凑微分法、直接代换法）

$$\begin{array}{c} \int f(g(x)) g^{\prime}(x) \mathrm{d} x \stackrel{u=g(x)}{=} \int f(u) \mathrm{d}(u) \\ \stackrel{\text { 积分 }}{=} F(u)+C \stackrel{\text { 回代 }}{=} F(g(x))+C . \end{array}$$

第二换元积分法（变量替换法）

设$x=\varphi(t)$可导，$\varphi^{\prime}(t) \neq 0$，并且$\int f(\varphi(t)) \varphi^{\prime}(t) \mathrm{d} t=G(t)+C$，则

$$\int f(x) \mathrm{d} x=G\left(\varphi^{-1}(x)\right)+C$$

常用的变换形式：

• $\sqrt{a^{2}-x^{2}}$型: 令$x=a \sin t, x=a \cos t$
• $\sqrt{x^{2}+a^{2}}$型: 令$x=a \tan t, x=a \cot t, x=a \sinh t$
• $\sqrt{x^{2}-a^{2}}$型: 令$x=a \sec t, x=\csc t, x=\cosh t$
• 分母出现$x^n$或$\sqrt[m]{ax^2+bx+c}$，令$t=\frac{1}{x}$
• 出现$\sqrt[n]{\frac{a x+b}{c x+d}}$：令$\sqrt[n]{\frac{a x+b}{c x+d}}=t$

分部积分法

$$\int u \mathrm{d} v=u v-\int v \mathrm{d} u$$

• 应用时注意“反对幂指三”或“反对幂三指”

• 分部积分的循环运用
  被积函数中含有根式、指数函数与三角函数乘积时，有可能会形成循环。

  例：$\int e^{a x} \cos b x \mathrm{~d} x$

  $$\begin{array}{l} &\int e^{a x} \cos b x \mathrm{~d} x\\ =&\frac{1}{a} \int \cos b x \mathrm{~d}\left(e^{a x}\right) \\ =&\frac{1}{a} e^{a x} \cos b x-\frac{1}{a} \int e^{a x} \mathrm{~d}(\cos b x) \\ =&\frac{1}{a} e^{a x} \cos b x+\frac{b}{a} \int e^{a x} \sin b x \mathrm{~d} x \\ =&\frac{1}{a} e^{a x} \cos b x+\frac{b}{a^{2}} \sin b x e^{a x}-\frac{b}{a^{2}} \int e^{a x} \mathrm{~d}(\sin b x) \\ =&\frac{1}{a} e^{a x} \cos b x+\frac{b}{a^{2}} \sin b x e^{a x}-\frac{b^{2}}{a^{2}} \int e^{a x} \cos b x \mathrm{~d}x \end{array}$$

  两边的$\int e^{a x} \cos b x \mathrm{~d} x$合并, 可求解出结果.

可积与不可积

• 不是所有的函数都有原函数
• 有的函数，尽管原函数存在，但是不能表达为初等函数的形式
• 如果原函数是初等函数,我们通常就说积分可以积出来
• 如果原函数存在，但是不是初等函数，我们就说积分积不出来
• 黎曼函数在$[0,1]$上可积
• 已经证明的“积分积不出来”的函数有
  • $\int_{-\infty}^{+\infty} e^{-x^{2}} \mathrm{~d} x=\sqrt{\pi}$ : Gauss 积分, 概率论 (Gauss, 1777-1855, 德国)
  • $\int_{0}^{+\infty} \frac{\sin x}{x} \mathrm{~d} x=\frac{\pi}{2}$ : Dirichlet 积分
  • $\int_{2}^{x} \frac{1}{\ln t} d t \sim \pi(x)$ : Euler 对数积分, 数论 (Euler, 1707-1783, 瑞士, $f(x), e, \pi, i, \sum,$ 拓扑、图论等若干数学分支的奠基者）
  • $\int_{0}^{\infty} \sin \left(x^{2}\right) \mathrm{d} x=\sqrt{\frac{\pi}{8}}$ : Fresnel 积分, 光学 (Fresnel, 1788-1827, 法国, 工程师、物理学家)
  • $\int_{0}^{\pi / 2} \sqrt{1-\varepsilon^{2} \cos ^{2} x} \mathrm{~d} x (0<\varepsilon<1)$ : 椭圆积分，代数、数论等，比特币
• 可积的充要条件——勒贝格定理
  • 定义：设数集$E\subset \mathbb{R},\forall \varepsilon > 0$，存在可数个开区间列$\{x_n\}$覆盖了$E$，而$\sum_{n=1}^{+\infty} |x_n|<\varepsilon$，则称数集$E$是零集，其中$|x_n|$表示$x_n$的长度。
  • 定理：有限个点所成的集合是零集；可数个点所成的集合是零集；可数个可数集的并集是零集。注意：不可数集也可能是零集。在$[a,b]$严格增加或减少的函数f(x)的间断点是零集。
  • 勒贝格定理：在区间$[a,b]$上有界函数 $f(x)$黎曼可积的充分必要条件是$[a, b]$所有间断点是零集。不是可数集的零集同样成立。

有理函数的不定积分

理论来说，任意有理函数的不定积分都可以归结为

$$\int \frac{\mathrm{d} x}{(x-a)^{m}}, \quad \int \frac{B x+C}{\left(x^{2}+p x+q\right)^{n}} \mathrm{~d} x$$

（其中$k\ge 1,p^2-4q<0$）
并表示为有理函数、对数函数和反正切函数的线性组合。

• $$\int \frac{\mathrm{d} x}{(x-a)^{m}} = \left\{\begin{array}{c} \ln|x-a|+C,&m=1\\ \frac{(x-a)^{-m+1}}{-m+1}+C,&m\ne 1 \end{array}\right.$$
• $$\begin{array}{l} \int \frac{1}{x^2+bx+c} d x&= \int \frac{1}{(x+\frac{b}{2})^2+c-\frac{b^2}{4}} d x\\ &= \int \frac{d(u)}{u^2+c-\frac{b^2}{4}}\text{（令}u=x+\frac{b}{2}\text{）} \\ &=\left\{\begin{array}{l} \int \frac{d(u)}{u^2},&c-\frac{b^2}{4}=0\\ \int \frac{d(u)}{u^2+a^2},&c-\frac{b^2}{4}\overset{\Delta}{=}a^2>0\\ \int \frac{d(u)}{u^2-a^2},&\frac{b^2}{4}-c\overset{\Delta}{=}a^2>0 \end{array}\right.\\ &= \left\{\begin{array}{l} -\frac{1}{u}+C,&c-\frac{b^2}{4}=0\\ \frac{1}{a}\arctan{\frac{u}{a}}+C,&c-\frac{b^2}{4}\overset{\Delta}{=}a^2>0\\ \frac{1}{2a}\ln|\frac{u-a}{u+a}|+C,&\frac{b^2}{4}-c\overset{\Delta}{=}a^2>0 \end{array}\right.\\ &\overset{\Delta}{=} dif(b,c,0) \end{array}$$
• $$\begin{array}{l} \int \frac{x}{x^2+bx+c} d x&= \frac{1}{2}\int \frac{d(x^2+bx+c)}{x^2+bx+c}-\frac{b}{2}\int \frac{d x}{x^2+bx+c}\\ &= \frac{1}{2}\ln|x^2+bx+c|-\frac{b}{2}dif(b,c,0)+C\\ &\overset{\Delta}{=} dif(b,c,1) \end{array}$$
• $$\begin{array}{l} \int \frac{x^2}{x^2+bx+c} d x&= \int (1-\frac{bx+c}{x^2+bx+c})dx\\ &= x-b\cdot dif(b,c,1)-c\cdot dif(b,c,0)+C\\ &= x-\frac{b}{2}\ln|x^2+bx+c|+(\frac{b^2}{2}-c)dif(b,c,0)+C\\ &\overset{\Delta}{=} dif(b,c,2) \end{array}$$
• $$\begin{aligned} \int \frac{B x+D}{x^{2}+p x+q} \mathrm{~d} x &=\frac{B}{2} \int \frac{\mathrm{d}\left(x^{2}+p x+q\right)}{x^{2}+p x+q}+\frac{2 D-B p}{2} \int \frac{\mathrm{d}\left(x+\frac{p}{2}\right)}{\left(x+\frac{p}{2}\right)^{2}+\frac{4q-p^2}{4}} \\ &=\frac{B}{2} \ln \left(x^{2}+p x+q\right)+\frac{2 D-B p}{\sqrt{4q-p^2}} \arctan \left(\frac{2 x+p}{\sqrt{4q-p^2}}\right)+C . \end{aligned}$$
• $$\int \frac{B x+D}{\left(x^{2}+p x+q\right)^{k}} \mathrm{~d} x=\frac{B}{2} \int \frac{\mathrm{d}\left(x^{2}+p x+q\right)}{\left(x^{2}+p x+q\right)^{k}}+\frac{2 D-B p}{2} \int \frac{\mathrm{d}\left(x+\frac{p}{2}\right)}{\left[\left(x+\frac{p}{2}\right)^{2}+\left(\frac{\sqrt{-\Delta}}{2}\right)^{2}\right]^{k}}$$

有理真分式的部分分式展开法

略

三角函数有理式的不定积分

• $\int R(\sin x)\cos x\mathrm{d}x$和$\int R(\cos x)\sin x\mathrm{d}x$型
  第一换元法
• $\int R(\sin^2 x,\cos^2 x)\mathrm{d}x$型
  令$t=\tan x$
• $\int \cos mx\cos nx\mathrm{d}x$、$\int \sin mx\sin nx\mathrm{d}x$和$\int \cos mx\sin nx\mathrm{d}x$型
  积化和差
• 对于一般的$\int R(\sin x,\cos x)\mathrm{d}x$
  令$t=\tan\frac{x}{2}$，万能代换 $$\int R(\sin x, \cos x) \mathrm{d} x=\int R\left(\frac{2 t}{1+t^{2}}, \frac{1-t^{2}}{1+t^{2}}\right) \frac{2 \mathrm{d} t}{1+t^{2}}$$

定积分的分部积分法

设$u^{\prime}(x), v^{\prime}(x) \in R[a, b]$，则

$$\int_{a}^{b} u v^{\prime} \mathrm{d} x=\left.u v\right|_{a} ^{b}-\int_{a}^{b} v u^{\prime} \mathrm{d} x$$

常见定积分

• Wallis公式（点火公式） $$\star \int_{0}^{\frac{\pi}{2}} \sin ^{n} x \mathrm{~d} x=\int_{0}^{\frac{\pi}{2}} \cos^{n} x \mathrm{~d} x=\left\{\begin{array}{ll} \frac{\pi}{2} \frac{(2 k-1) ! !}{(2 k) ! !}, & n=2 k \\ \frac{(2 k) ! !}{(2 k+1) ! !}, & n=2 k+1 \end{array}\right.$$
  • $$\lim _{k \rightarrow \infty}\left[\frac{(2 k) ! !}{(2 k-1) ! !}\right]^{2} \cdot \frac{1}{2 k+1}=\frac{\pi}{2}$$

定积分的变量替换法

设 $f(x) \in C(I)$, $F^{\prime}(u)=f(u)$, $\varphi^{\prime}(x) \in$ $C[a, b]$，且 $R(\varphi) \subset I$，则

$$\int_{b}^{a} f(\varphi(x)) \varphi^{\prime}(x) \mathrm{d} x=\left.F(\varphi(x))\right|_{a} ^{b}$$

定积分的换元积分法

设$f(x) \in C[a, b]$，而 $x=\varphi(t)$ 满足:

• $\varphi(\alpha)=a, \varphi(\beta)=b $
• $\varphi^{\prime}(t) \in R[\alpha, \beta]$，且 $\varphi([\alpha, \beta])=[a, b] $
  则有 $$\int_{a}^{b} f(x) \mathrm{d} x=\int_{\alpha}^{\beta} f(\varphi(t)) \varphi^{\prime}(t) \mathrm{d} t$$

换元常用公式（以下均为$f(x)$连续）

• 若$f(x)$为偶函数, 则 $$\int_{-a}^{a} f(x) \mathrm{d} x=2 \int_{0}^{a} f(x) \mathrm{d} x$$
• 若$f(x)$为奇函数, 则 $$\int_{-a}^{a} f(x) \mathrm{d} x=0$$
• 若$f(x)$为周期$T$的函数,则 $$\int_{a}^{a+n T} f(x) \mathrm{d} x=n \int_{0}^{T} f(x) \mathrm{d} x$$
• 正余弦互换 $$\int_{0}^{\frac{\pi}{2}} f(\sin x, \cos x) \mathrm{d} x=\int_{0}^{\frac{\pi}{2}} f(\cos x, \sin x) \mathrm{d} x$$
• 正弦对称区间 $$\int_{0}^{\pi} f(\sin x) \mathrm{d} x=2 \int_{0}^{\frac{\pi}{2}} f(\sin x) \mathrm{d} x$$
• $x f(\sin x)$型 $$\int_{0}^{\pi} x f(\sin x) \mathrm{d} x=\frac{\pi}{2} \int_{0}^{\pi} f(\sin x) \mathrm{d} x$$
• 区间再现公式 $$\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(a+b-x) \mathrm{d} x$$

关于循环

• 定积分换元后循环，可以移项得到结论（变量只是工具，无关联）
• 不定积分换元后循环不能移项得到结论（换元前后变量有关联）
• 不定积分里，分部积分循环，可以移项得出结论（分部积分并没有引入新变量）
• 牢记：不定积分是函数，定积分是值

解简单的积分方程

• 变限积分方程，求导解决
• 定积分方程，令定积分=t

直角坐标系下的平面图形面积

• 由直线$x=a, x=b(a<b)$以及连续曲线$y=f_{1}(x), y=f_{2}(x)$围成的平面图形的面积为 $$S=\int_{a}^{b}\left|f_{2}(x)-f_{1}(x)\right| \mathrm{d} x$$
• 由直线$y=c, y=d(c<d)$以及连续曲线$x=g_{1}(y), x=g_{2}(y)$围成的平面图形的面积为 $$S=\int_{c}^{d}\left|g_{2}(y)-g_{1}(y)\right| \mathrm{d} y$$

参数方程下平面图形的面积

曲线$C$的方程为$\left\{\begin{array}{l}x=x(t) \\ y=y(t)\end{array} \quad t \in[\alpha, \beta]\right.$
其中$x^{\prime}(t), y(t) \in C[\alpha, \beta]$，且$x^{\prime}(t) \neq 0$
记$x(\alpha)=a, x(\beta)=b$，则曲线$C, x=a, x=b$及$x$轴围成的图形面积为

$$S=\int_{\alpha}^{\beta}\left|y(t) x^{\prime}(t)\right| \mathrm{d} t$$

$y^{\prime}(t) \neq 0$可类似讨论。

极坐标下平面图形的面积

曲线$C$的方程为$r=r(\theta), r(\theta) \in C[\alpha, \beta]$
则由$\theta=\alpha, \theta=\beta$与$r=r(\theta)$所围成图形的面积为

$$S=\frac{1}{2} \int_{\alpha}^{\beta} r^{2}(\theta) \mathrm{d} \theta$$

基本图形的面积

• 心脏线:$r=2 a(1+\cos \theta)(a>0)$ $$S=2 \cdot \frac{1}{2} \int_{0}^{\pi} a^{2}(1+\cos \theta)^{2} \mathrm{~d} \theta=\frac{3}{2} \pi a^{2}$$
• 星形线:$x=a \cos ^{3} t, y=a \sin ^{3} t, t \in[0,2 \pi]$ $$S=4 \cdot \int_{0}^{\frac{\pi}{2}}\left|a \sin ^{3} t\left(a \cos ^{3} t\right)^{\prime}\right| \mathrm{d} t=\cdots=\frac{3}{8} \pi a^{2}$$
• 椭圆:$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a, b>0)$ $$S=\pi ab$$
• 双扭线:$\left(x^{2}+y^{2}\right)^{2}=a^{2}\left(x^{2}-y^{2}\right)$ $$S=4 \cdot \frac{1}{2} \int_{0}^{\frac{\pi}{4}} a^{2} \cos 2 \theta \mathrm{d} \theta=\cdots=a^{2}$$

平面曲线的弧长

（注意：并不是所有的曲线都可求长）

• 直角坐标系下平面曲线的弧长
  • 曲线：$y=f(x)$, $x \in[a, b]$, $f^{\prime}(x) \in C[a, b]$
  • 弧微分：$\mathrm{d} s=\sqrt{1+f^{\prime 2}(x)} \mathrm{d} x $
  • 弧长：$s=\int_{a}^{b} \sqrt{1+f^{\prime 2}(x)} \mathrm{d} x $
• 参数方程下平面曲线的弧长
  • 曲线：$x=x(t), y=y(t)$, $t \in[\alpha, \beta]$, $x^{\prime}(t)$, $y^{\prime}(x) \in C[\alpha, \beta]$
  • 弧微分：$\mathrm{d} s=\sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} \mathrm{d} t $
  • 弧长：$s=\int_{\alpha}^{\beta} \sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} \mathrm{d} t$
• 极坐标下平面曲线的弧长
  • 曲线：$r=r(\theta), \theta \in[\alpha, \beta]$, $r^{\prime}(\theta)=C[\alpha, \beta]$
  • 弧微分：$\mathrm{d} s=\sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} \mathrm{d} \theta$
  • 弧长：$s=\int_{\alpha}^{\beta} \sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} \mathrm{d} \theta$
  • 曲线：$\theta=f(r), r\in[\alpha, \beta]$ , $f(r) \in C[\alpha, \beta]$
  • 弧长：$s=\int_{\alpha}^{\beta} \sqrt{1+r^{2}f^{\prime 2}(r)} \mathrm{d} r$

基本图形的周长

• 星形线：$x=a \cos ^{3} t, y=a \sin ^{3} t, t \in[0,2 \pi]$ $$C=6a$$
• 心脏线：$r=2 a(1+\cos \theta)$ $$C=8a$$
• 椭圆：$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ $$C=4a\int_0^{\frac{\pi}{2}}\sqrt{1-\left(1-\frac{b^2}{a^2}\right)\cos^2\theta}\mathrm{d}\theta\quad\text{椭圆积分}$$

曲率

• 若曲线由$y=y(x)$表示，则曲率 $$\kappa=\frac{\left|y^{\prime \prime}(x)\right|}{\left[1+y^{\prime 2}(x)\right]^{3 / 2}}$$
• 若曲线由参数方程$x=x(t), y=y(t)$表示，则曲率 $$\kappa=\frac{\left|x^{\prime}(t) y^{\prime \prime}(t)-x^{\prime \prime}(t) y^{\prime}(t)\right|}{\left[x^{\prime 2}(t)+y^{\prime 2}(t)\right]^{\frac{3}{2}}} .$$
• 若曲线由极坐标方程$r=r(\theta)$表示，则曲率 $$\kappa=\frac{\left|r^{2}(\theta)+2 r^{\prime 2}(\theta)-r(\theta) r^{\prime \prime}(\theta)\right|}{\left[r^{2}(\theta)+\left(r^{\prime 2}(\theta)\right)\right]^{3 / 2}}$$
• 半径为$r=\frac{1}{\kappa}$的圆是曲率圆

立体体积的微元法

设立体位于平面$x=a, x=b$之间$(a<b)$,$\forall x \in[a, b]$, 用垂直于$x$轴的平面截立体，截面面积为$A(x) \in C[a, b]$
体积微元$\mathrm{d}V=A(x) \mathrm{d} x$, 故体积$V=\int_{a}^{b} A(x) \mathrm{d} x$
先求出截面面积，积分即可得到立体的体积。

旋转体体积

• 薄片法
  旋转体由连续曲线$y= f (x)$,$x=a$,$x=b(a<b)$与$x$轴围成图形绕$x$轴旋转一周形成。

  • 截面面积函数为$A(x)=\pi f^2(x)$
  • 体积微元$\mathrm{d}V =\pi f^2(x)\mathrm{d}x$
  • 旋转体体积$V=\pi\int_a^b f^2(x)\mathrm{d}x$

  由连续函数$x= g(y)$,$y= c$,$y=d(c<d)$与$y$轴围成的图形绕$y$轴旋转得到的旋转体的体积为

  $$V=\pi\int_c^d g^2(y)\mathrm{d}y$$

  若连续函数由参数形式给出:$x = x(t)$,$y = y(t)$, $t\in [\alpha,\beta]$, $y’(t) , x’(t)\in C[\alpha,\beta]$，绕$x$轴旋转，则旋转体体积为

  $$V=\pi\int_\alpha^\beta |y^2(t)x'(t)|\mathrm{d}t$$

• 薄壳法
  由连续曲线$y = f(x)$,$x = a$,$x = b(a<b)$与$x$轴围成图形，绕$y$轴旋转一周形成旋转体。

  • 体积微元：$\mathrm{d} V=2 \pi x f(x) \mathrm{d} x$
  • 立体的体积：$V=2 \pi \int_{a}^{b} x f(x) \mathrm{d} x$

旋转曲面的侧面积

微元法，用圆台侧面积近似表示旋转曲面的侧面积微元。

• 直角坐标系下旋转曲面的侧面积
  设非负光滑曲线$y=f(x)$,$x \in[a, b]$，绕$x$轴旋转一周形成的旋转曲面的面积为 $$S=2 \pi \int_{a}^{b} f(x) \sqrt{1+f^{\prime 2}(x)} \mathrm{d} x$$
• 参数方程下旋转曲面的侧面积
  非负光滑曲线为$C: x=x(t)$,$y=y(t)$,$t \in [\alpha, \beta]$，则曲线绕$x$轴旋转形成的旋转体侧面积为 $$S=2 \pi \int_{\alpha}^{\beta} y(t) \sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} \mathrm{d} t$$
• 极坐标系下旋转曲面的侧面积
  非负光滑曲线为$C: r=r(\theta)$,$ \theta \in[\alpha, \beta]$，则曲线绕极轴旋转形成的旋转体侧面积为 $$S=2 \pi \int_{\alpha}^{\beta} r(\theta) \sin \theta \sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} d \theta$$

注意区分旋转面的侧面积和旋转体的表面积。

反常积分（广义积分）

• 无穷积分：积分区间无限的情况
• 瑕积分：被积函数无界的情况
• 这两种积分统称为反常积分，广义积分
• 之前学习的定积分称为常义积分

无穷积分

• 定义
  设$f(x), x \in[a,+\infty)$，若$\forall b>a$,$f(x) \in R[a, b]$，则称形式积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$为$f(x)$在无穷区间$[a,+\infty)$上的反常积分（无穷积分）。

• 敛散性定义
  令$F(b)=\int_{a}^{b} f(x) \mathrm{d} x$。若极限$\lim_{b \rightarrow+\infty} F(b)$存在，收敛到$I$（有限存在，非无穷），则称反常积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛，且定义其值为

  $$\int_{a}^{+\infty} f(x) \mathrm{d} x=\lim _{b \rightarrow+\infty} \int_{a}^{b} f(x) \mathrm{d} x=I .$$

  否则称$f(x)$在$[a,+\infty)$上的无穷积分发散。

• 几何意义
  函数$f(x) \geqslant 0$,$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛 表示由曲线$y=f(x)$,直线$x=a$和$x$轴所围成的向右无限伸展的图形面积有限。

• 敛散性判断定理
  设$f(x) \in C[a,+\infty)$,$F(x)$是它在$[a,+\infty)$上的一个原函数，由N-L公式，

  $$\int_{a}^{+\infty} f(x) \mathrm{d} x=\left.\lim _{b \rightarrow+\infty} F(x)\right|_{a} ^{b}=\lim _{b \rightarrow+\infty} F(b)-F(a)$$

  故无穷积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$的敛散性等价于函数极限$\lim_{b \rightarrow+\infty} F(b)$的敛散性。

• 双向无穷积分敛散性
  设$f(x), x \in \mathbb{R}$，若$\exists a \in \mathbb{R}$，无穷积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$,$\int_{-\infty}^{a} f(x) \mathrm{d} x$均收敛，则称无穷积分收敛，且定义其值为

  $$\int_{-\infty}^{+\infty} f(x) \mathrm{d} x=\int_{-\infty}^{a} f(x) \mathrm{d} x+\int_{a}^{+\infty} f(x) \mathrm{d} x$$

  否则称无穷积分$\int_{-\infty}^{+\infty} f(x) \mathrm{d} x$发散。

瑕积分

• 定义
  若$f(x)$在$a$点的任一邻域内无界，则称$a$点 为$f(x)$的奇点或者瑕点。
  设$f(x), x \in(a, b]$，若$a$是$f(x)$的一个瑕点而在任一区间$\forall \epsilon>0$,$f(x) \in R[a+\epsilon, b]$，则称形式积分$\int_{a}^{b} f(x) \mathrm{d} x$为$f(x)$在$(a, b]$上的反常积分，又称为瑕积分，$a$为瑕点。
  类似可定义瑕积分$\int_{a}^{b} f(x) \mathrm{d} x$，$x = b$为瑕点。
• 敛散性
  若极限$\lim_{\epsilon \rightarrow 0^{+}} \int_{a+\epsilon}^{b} f(x) \mathrm{d} x$(有限) 存在，称瑕积分$\int_{a}^{b} f(x) \mathrm{d} x$收敛，且积分值为 $$\int_{a}^{b} f(x) \mathrm{d} x=\lim _{\epsilon \rightarrow 0^{+}} \int_{a+\epsilon}^{b} f(x) \mathrm{d} x .$$ 否则称瑕积分$\int_{a}^{b} f(x) \mathrm{d} x$发散。
• 区间内瑕点
  设$c \in[a, b]$是$f(x)$在$[a, b]$区间上唯一的瑕点。若瑕积分$\int_{a}^{c} f(x) \mathrm{d} x$,$\int_{c}^{b} f(x) \mathrm{d} x$均收敛，则称瑕积分$\int_{a}^{b} f(x) \mathrm{d} x$收敛，且定义其值为$\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x$

常见敛散性判断

• 无穷积分$\int_{1}^{+\infty} \frac{1}{x^{p}} \mathrm{d} x$
  • $p>1$时收敛于$\frac{1}{p-1}$
  • $p \leqslant 1$时发散
• 瑕积分$\int_{0}^{1} \frac{\mathrm{d} x}{x^{p}}$,$\int_{a}^{b} \frac{\mathrm{d} x}{(x-a)^{p}}$,$\int_{a}^{b} \frac{\mathrm{d} x}{(x-b)^{p}}$ $(p \in \mathbb{R})$
  • $p<1$时收敛
  • $p \geqslant 1$时发散

无穷积分与瑕积分的互相转化

• 对瑕积分$\int_{a}^{b} f(x) \mathrm{d} x$，$x=a$为瑕点，令

  $$x=a+\frac{1}{y}\left(y=\frac{1}{x-a}\right)$$

  瑕积分可化为无穷积分

• 对无穷积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$，令

  $$x=\frac{a}{y}$$

  无穷积分可化为瑕积分

Heine归并定理

无穷积分$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛的充要条件是

• $$\forall\left\{A_{n}\right\} \subset[a,+\infty), \lim _{n \rightarrow \infty} A_{n}=+\infty$$
• 极限$\lim_{n \rightarrow \infty} \int_{a}^{A_{n}} f(x) \mathrm{d} x$均存在且相等

逆否命题判别发散。

非负函数无穷积分的判敛法

设$f(x)$和$g(x)$非负，均在任意有界区间上可积。
(1)$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛的充要条件是$F(A)=\int_{a}^{A} f(x) \mathrm{d} x$在$[a,+\infty)$上有上界
(2) 比较法：若$0 \leqslant f(x) \leqslant g(x)$，则：

• $\int_{a}^{+\infty} g(x) \mathrm{d} x$收敛时，$\int_{a}^{+\infty} f(x) \mathrm{d} x$也收敛;
• $\int_{a}^{+\infty} f(x) \mathrm{d} x$发散时，$\int_{a}^{+\infty} g(x) \mathrm{d} x$也发散。
  (3) 以$p$积分为比较函数，可以得到$p$判别法。

一般函数无穷积分判敛法：AD判别法

• Abel判别法：设$g(x)$在$[a,+\infty)$上单调有界，$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛，则$\int_{a}^{+\infty} f(x) g(x) \mathrm{d} x$收敛。
• Dirichlet判别法：设$F(A)=\int_{a}^{A} f(x) \mathrm{d} x$在$[a,+\infty)$上有界，$g(x)$在$[a,+\infty)$上单调，且$\lim_{x \rightarrow+\infty} g(x)=0$，则$\int_{a}^{+\infty} f(x) g(x) \mathrm{d} x$收敛。

无穷积分的函数性质

• $\lim_{x \rightarrow+\infty} f(x)=0 \nRightarrow \int_{a}^{+\infty} f(x) \mathrm{d} x$收敛
• $\lim_{x \rightarrow+\infty} f(x)=c \neq 0$，则$\int_{a}^{+\infty} f(x) \mathrm{d} x$发散
• 无穷积分收敛$\nRightarrow \lim_{x \rightarrow+\infty} f(x)=0 $
• 可以构造出$f(x)$在$[a,+\infty)$上恒正连续 且无界，而$\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛的例子。
• $\int_{a}^{+\infty} f(x) \mathrm{d} x$收敛。若$\lim_{x \rightarrow+\infty} f(x)$存在，或者$f(x)$在$[a,+\infty)$上单调，则$\lim_{x \rightarrow+\infty} f(x)=0$

第六章 微分方程

微分方程相关定义

• 微分方程，微分方程的阶数
• 微分方程的解，通解，特解
• 微分方程的定解条件，定解问题
• 初值条件(Cauchy条件)，初值问题(Cauchy问题)
• 一阶微分方程的初值问题 $$\left\{\begin{array}{l} y^{\prime}=f(x, y) \\ \left.y\right|_{x=x_{0}}=y_{0} \end{array}\right.$$
• 二阶微分方程的初值问题 $$\left\{\begin{array}{l} y^{\prime \prime}=f\left(x, y, y^{\prime}\right) \\ \left.y\right|_{x=x_{0}}=y_{0} \\ \left.y^{\prime}\right|_{x=x_{0}}=y_{1} \end{array}\right.$$

一阶微分方程

一阶微分方程的一般形式：$F\left(x, y, y^{\prime}\right)=0$
主要讨论$y^{\prime}=f(x, y)$形式的一阶微分方程。
有时也写成$P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=0$的形式

可分离变量方程

• 形式：$\frac{\mathrm{d} y}{\mathrm{d} x}=\varphi(x) \psi(y)$
• 解法：化为$\frac{1}{\psi(y)} \mathrm{d} y=\varphi(x) \mathrm{d} x$后两边积分
• 注意：$\psi(y)=0$ 得到的 $y=Const$ 也是方程的解
• 注意：某些情况下积分后绝对值可以借助任意常数拿掉

有些方程经过变换可化为可分离变量的方程。
如$\frac{\mathrm{d} y}{\mathrm{d} x}=f(a x+b y+c), \quad(b \neq 0)$
令$a x+b y+c=u(x) \Longrightarrow \frac{\mathrm{d} u}{\mathrm{d} x}=b f(u)+a$
分离变量，变量回代，注意隐式解, 特解;

齐次微分方程

• 判定：
  形如 $\frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{y}{x}\right)$ 的方程称为齐次微分方程。
  一般地，$\frac{\mathrm{d} y}{\mathrm{d} x}=\phi(x, y)$，如果 $\phi(x, y)$ 满足 $\phi(t x, t y)=\phi(x, y)$ ，则 $\phi(x, y)$ 一定可以化为 $f\left(\frac{y}{x}\right)$ 形式。
• 求解：
  $\frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{y}{x}\right)$. 令$\frac{y}{x}=u(x) $ 即 $y=x u(x)$ $\Longrightarrow$ $\frac{\mathrm{d} u}{f(u)-u}=\frac{\mathrm{d} x}{x}$

上下一次分式型

形如$\frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{a_{1} x+b_{1} y+c_{1}}{a_{2} x+b_{2} y+c_{2}}\right)$ $\left(a_{1}: a_{2} \neq b_{1}: b_{2}\right)$的方程可化为齐次方程。

• $c_{1}=c_{2}=0$，即为齐次方程
• $c_{1}, c_{2}$ 不同时为 $0$ , 不是齐次方程
  令 $X=x-x_{0}, Y=y-y_{0}$ , 其中 $x_{0}, y_{0}$ 满足 $$\left\{\begin{array}{l} a_{1} x+b_{1} y+c_{1}=0 \\ a_{2} x+b_{2} y+c_{2}=0 \end{array}\right.$$ 则原方程可以化为 $\frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{a_{1} X+b_{1} Y}{a_{2} X+b_{2} Y}\right)$，为齐次方程。

一阶线性微分方程

一阶线性(linear)微分方程：$y^{\prime}+P(x) y=Q(x)$，其中 $P(x), Q(x)$ 连续。$Q(x)$ 称为非齐次项或自由项。

• $Q(x)=0$ , 称为一阶线性齐次(homogeneous)微分方程 ($1-\mathrm{LH}$)
  可分离变量，方程的解为 $$y=C e^{-\int P(x) \mathrm{d} x}\left(\int P(x) \mathrm{d} x\right. \text{表示一个原函数} )$$
• $Q(x) \neq 0$,$y^{\prime}+P(x) y=Q(x)$ 称为一阶线性非齐次(non-homogeneous)微分方程($1-\mathrm{LNH}$)
  通常用常数变易法求解：
  已知它对应的齐次方程 $y^{\prime}+P(x) y=0$ 的通解为$y=C e^{-\int P(x) \mathrm{d} x}$，设$y=C(x) e^{-\int P(x) \mathrm{d} x}$为$y^{\prime}+P(x) y=Q(x)$的解， 则可推出 $$\begin{aligned} y &=e^{-\int P(x) \mathrm{d} x}\left(\int Q(x) e^{\int P(x) \mathrm{d} x} \mathrm{d} x+C\right) \\ &=C e^{-\int P(x) \mathrm{d} x}+e^{-\int P(x) \mathrm{d} x} \cdot \int Q(x) e^{\int P(x) \mathrm{d} x} \end{aligned}$$ 由对应的一阶线性齐次微分方程的通解和一个 线性非齐次微分方程的特解组成。

Bernoulli方程

形如

$$y^{\prime}+P(x) y=Q(x) y^{\alpha}, \quad(\alpha \neq 0,1)$$

的方程称为Bernoulli方程。
解法：令 $z=y^{1-\alpha}$，Bernoulli方程可化为

$$z^{\prime}+(1-\alpha) P(x) z=(1-\alpha) Q(x) .$$

（一阶线性非齐次微分方程）
$y=0$亦为原方程的解，不要遗漏!

可降阶的高阶微分方程

• $y^{(n)}=f(x)$ 型方程
  每积分一次，就降阶一次。逐次积分得出通解
• $y^{\prime \prime}=f\left(x, y^{\prime}\right)$ 型方程（含 $y^{\prime \prime}, y^{\prime}$ 项, 不显含 $y$ 项）
  令 $\frac{\mathrm{d} y}{\mathrm{d} x}=p(x) \Longrightarrow \frac{\mathrm{d} p}{\mathrm{d} x}=f(x, p)$ 降阶
• $y^{\prime \prime}=f\left(y, y^{\prime}\right)$ 型方程（不显含$x$）
  令 $\frac{\mathrm{d} y}{\mathrm{d} x}=p(y) \Longrightarrow p(y) \cdot \frac{\mathrm{d} p}{\mathrm{d} y}=f(y, p)$ 降阶

线性微分方程解的结构

$n$ 阶线性微分方程的标准形式为

$$y^{(n)}+p_{1}(x) y^{(n-1)}+\cdots+p_{n-1}(x) y^{\prime}+p_{n}(x) y=f(x)$$

其中 $p_{1}(x), \cdots, p_{n}(x), f(x)$ 为已知的连续函数，$f(x)$称为自由项，或非齐次项。

• $f(x) \equiv 0$: $n$ 阶线性齐次微分方程 ($n-\mathrm{LH}$)
• $f(x)$不恒等于$0$: $n$ 阶线性非齐次微分方程 ($n-\mathrm{LNH}$)

线性微分方程解的叠加原理

如果 $y_{1}(x), y_{2}(x)$ 分别是方程

$$\begin{array}{l} y^{(n)}+p_{1}(x) y^{(n-1)}+\cdots+p_{n}(x) y=f_{1}(x) \\ y^{(n)}+p_{1}(x) y^{(n-1)}+\cdots+p_{n}(x) y=f_{2}(x) \end{array}$$

的解，则 $c_{1} y_{1}(x)+c_{2} y_{2}(x)$ 是方程

$$y^{(n)}+p_{1}(x) y^{(n-1)}+\cdots+p_{n}(x) y=c_{1} f_{1}(x)+c_{2} f_{2}(x)$$

的解（$c_{1}, c_{2}$为任意常数）

• 推论 1： 如果 $y_{1}(x), y_{2}(x)$ 是线性齐次方程的解, 则 $c_{1} y_{1}(x)+c_{2} y_{2}(x)$（$c_{1}, c_{2}$是任意常数）也是该线性齐次方程的解($\mathrm{H}+\mathrm{H}=\mathrm{H}$)
• 推论 2： 线性非齐次方程的解加上相应的线性齐次方程的解，依然是该线性非齐次方程的解 ($\mathrm{N}+\mathrm{H}=\mathrm{N}$)
• 推论 3： 若 $y_{1}, y_{2}$ 为线性非齐次方程的两个解，则 $y_{1}-y_{2}$ 是相应的线性齐次微分方程的解 ($\mathrm{N}-\mathrm{N}=\mathrm{H}$)

二阶线性齐次微分方程解的结构

二阶线性齐次微分方程标准形式

$$y^{\prime \prime}+p(x) y^{\prime}+q(x) y=0$$

其中 $p(x), q(x)$ 连续。
显然 $y=0$ 是方程的解，称为平凡解。
除平凡解外，其他解称为非平凡解。

由叠加原理，$y_{1}(x), y_{2}(x)$ 是方程$(\mathrm{HL})$ 的解，则 $c_{1} y_{1}(x)+c_{2} y_{2}(x)$ 也是 $(\mathrm{HL})$ 的解($c_{1}, c_{2}$是任意常数)

• 定理
  若 $y_{1}(x), y_{2}(x)$ 是方程$(\mathrm{HL})$的两个线性无关的特解，则 $$c_{1} y_{1}(x)+c_{2} y_{2}(x) (c_{1} , c_2 \text {为任意常数})$$ 是方程 $(\mathrm{HL})$ 的通解，给出方程所有的解。
  $y_{1}(x), y_{2}(x)$ 称为方程的基本解组。

Liouville公式

若知道一个非零特解，可用常数变易法求出另一线性无关解
定理3 (Liouville公式)：若 $y_{1}(x)$ 是$(\mathrm{HL})$的非零解，那么

$$y_{2}(x)=y_{1}(x) \int \frac{1}{y_{1}^{2}(x)} e^{-\int p(x) \mathrm{d} x} \mathrm{~d} x$$

是方程$(\mathrm{HL})$的另一解，且与 $y_{1}(x)$ 线性无关。

二阶线性非齐次微分方程解的结构

二阶线性非齐次方程的标准形式为

$$y^{\prime \prime}+p(x) y^{\prime}+q(x) y=f(x) \quad (\mathrm{NHL})$$

对应的线性齐次方程为

$$y^{\prime \prime}+p(x) y^{\prime}+q(x) y=0 \quad (\mathrm{HL})$$

定理3 (线性非齐次方程解的结构定理):
设 $y^{\star}(x)$ 是方程 $(\mathrm{NHL})$ 的解，$\bar{y}=C_{1} y_{1}(x)+C_{2} y_{2}(x)$ 是对应的方程 $(\mathrm{HL})$ 的通解，则 $y=y^{*}(x)+\bar{y}$ 是方程 $(\mathrm{NHL})$ 的通解。

如何求方程的一个特解

• $(\mathrm{HL})$方程
  常用的方法：观察法

• $(\mathrm{NHL})$方程
  常用的方法：观察法、叠加法、常数变易法、待定系数法

• 观察法：简单形式方程常用观察法找出特解
  $x^{m}, e^{\alpha x}, \sin m x, \cos m x$ 等

• 叠加法：利用线性方程解的叠加原理
• 常数变易法:
  所谓常数变易法就是先求出对应的线性齐次方程的通解，然后将通解中的任意常数换成待定的函数，代入方程，确定此函数，从而得到线性非齐次方程的解。
  （上面是废话）
  一般的解法:
  若$(\mathrm{HL})$ 的基本解组为$y_{1}(x), y_{2}(x)$，则设 $(\mathrm{NHL})$ 的特解为 $$y^{*}=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x)$$ $$\text{联立} \left\{\begin{array}{l}c_{1}^{\prime}(x) y_{1}(x)+c_{2}^{\prime}(x) y_{2}(x)=0 \\ c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)=f(x)\end{array}\right.$$ 解出 $c_{1}^{\prime}(x), c_{2}^{\prime}(x)$，从而求出 $c_{1}(x), c_{2}(x)$，得到方程 $(\mathrm{NHL})$ 的解。

微分方程解法总结

• 简单一阶线性方程

  $$\begin{array}{|l|l|} \hline 类型 & 解法 \\ \hline \frac{\mathrm{d} y}{\mathrm{d} x}=\varphi(x) \psi(y) & 分离变量 \\ \hline \frac{\mathrm{d} y}{\mathrm{d} x}=f(a x+b y+c) & \begin{array}{l} 令ax+by+c=u(x) \\ \Longrightarrow \frac{\mathrm{d} u}{\mathrm{d} x}=b f(u)+a ，分离变量\end{array} \\ \hline \frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{y}{x}\right) & \begin{array}{l} 令\frac{y}{x}=u(x) 即 y=x u(x) \\ \Longrightarrow \frac{\mathrm{d} u}{f(u)-u}=\frac{\mathrm{d} x}{x}\end{array} \\ \hline \begin{array}{l}\frac{\mathrm{d} y}{\mathrm{d} x}=f\left(\frac{a_{1} x+b_{1} y+c_{1}}{a_{2} x+b_{2} y+c_{2}}\right)\\ \left(a_{1}: a_{2} \neq b_{1}: b_{2}\right)\end{array} & \begin{array}{l} 令X=x-x_{0}, Y=y-y_{0}, \\其中x_{0}, y_{0}满足 \\\left\{\begin{array}{l} a_{1} x_0+b_{1} y_0+c_{1}=0 \\ a_{2} x_0+b_{2} y_0+c_{2}=0 \end{array}\right.\\则原方程可以化为齐次方程 \end{array} \\ \hline \end{array}$$

• 一阶线性方程

  $$\begin{array}{|l|l|} \hline 类型 & 解法 \\ \hline y^{\prime}+P(x) y=0 & y=C e^{-\int P(x) \mathrm{d} x} \\ \hline y^{\prime}+P(x) y=Q(x) & \begin{aligned} y &=e^{-\int P(x) \mathrm{d} x}\left(\int Q(x) e^{\int P(x) \mathrm{d} x} \mathrm{d} x+C\right) \\ &=C e^{-\int P(x) \mathrm{d} x}+e^{-\int P(x) \mathrm{d} x} \cdot \int Q(x) e^{\int P(x) \mathrm{d} x}\mathrm{d} x \\ &\text{（上面的不定积分都是指一个原函数）} \end{aligned} \\ \hline y^{\prime}+P(x) y=Q(x) y^{\alpha} & \begin{array}{l}y=0是一解\\令z=y^{1-\alpha},Bernoulli方程可化为 \\z^{\prime}+(1-\alpha) P(x) z=(1-\alpha) Q(x) \end{array}\\ \hline \end{array}$$

• 简单高阶线性方程

  $$\begin{array}{|l|l|} \hline 类型 & 解法 \\ \hline y^{(n)}=f(x) & 积分n次 \\ \hline y^{\prime \prime}=f\left(x, y^{\prime}\right) & 令\frac{\mathrm{d} y}{\mathrm{d} x}=p(x) \Longrightarrow \frac{\mathrm{d} p}{\mathrm{d} x}=f(x, p) 降阶\\ \hline y^{\prime \prime}=f\left(y, y^{\prime}\right) & 令\frac{\mathrm{d} y}{\mathrm{d} x}=p(y) \Longrightarrow p(y) \cdot \frac{\mathrm{d} p}{\mathrm{d} y}=f(y, p)降阶\\ \hline \end{array}$$

• 二阶线性微分方程

  • 先求解$(\mathrm{HL})$方程
    $y=0$是解
    常用的方法：观察法
  • 再求解$(\mathrm{NHL})$方程
    常用的方法：观察法、叠加法、常数变易法、待定系数法

二阶常系数线性齐次微分方程

二阶常系数线性齐次微分方程的标准形式：

$$y''+py'+qy=0\text{（其中}p, q\text{为实数）}$$

令$y = e^{rx}$，得到

$$r^2+pr+q=0$$

称为特征方程，它的两个根称为特征根。

$$r_{1,2}=\frac{-p \pm \sqrt{p^{2}-4 q}}{2} .$$

• 通解 $$\begin{array}{|c|c|} \hline \text { 特征根情况 } & \text { 通解形式 } \\ \hline \text { 相异实根 } r_{1}, r_{2} & c_{1} e^{r_{1} x}+c_{2} e^{r_{2} x} \\ \hline \text { 相同实根 } r & e^{r x}\left(c_{1}+c_{2} x\right) \\ \hline \text { 共轭复根 } \alpha \pm i \beta & e^{\alpha x}\left(c_{1} \cos \beta x+c_{2} \sin \beta x\right) \\ \hline \end{array}$$

n阶常系数线性齐次微分方程

$$y^{(n)}+p_{1} y^{(n-1)}+\cdots+p_{n-1} y^{\prime}+p_{n} y=0$$

其中 $p_{1}, \cdots, p_{n}$ 是实数。
令$y=e^{r x}$，代入上式，得

$$r^{n}+p_{1} r^{n-1}+\cdots p_{n-1} r+p_{n}=0$$

称为上面方程的特征方程。
根据特征根的情况，可以写出对应微分方程的解

• 通解：

  $$\begin{array}{|c|c|} \hline \text { 特征根 } & \text { 方程的通解 } \\ \hline \text { 单实根 } r & c e^{r x} \\ \hline k \text { 重实根 } r & e^{r x}\left(c_{1}+c_{2} x+\cdots c_{k} x^{k-1}\right) \\ \hline \begin{array}{c}\alpha \pm i \beta \\1 \text {重} \end{array} & e^{\alpha x}\left(c_{1} \cos \beta x+c_{2} \sin \beta x\right) \\ \hline \begin{array}{c}\alpha \pm i \beta \\k \text {重} \end{array} & \begin{array}{l} e^{\alpha x}\left[c_{1}+c_{2} x+\cdots c_{k} x^{k-1}\right] \cos \beta x \\ +e^{\alpha x}\left[c_{k+1}+c_{k+2} x+\cdots c_{2 k} x^{k-1}\right] \sin \beta x \end{array} \\ \hline \end{array}$$

• 留意常系数线性齐次微分方程的解的特点，可由解反推出方程。

二阶常系数线性非齐次微分方程

• 一般形式 $$y''+py'+qy=f(x)$$
• 一般解法：常数变易法

特殊的常系数线性非齐次微分方程

非齐次项$f(x)$为某些特殊形式时，则可用观察法、叠加法和待定系数法求特解。

下列两种 $f(x)$ 形式可用待定系数法：

• $f(x)=P_{m}(x) e^{\lambda x}$,$P_{m}(x)$是$m$次多项式
• $f(x)=e^{\lambda x}[P(x) \cos \mu x+Q(x) \sin \mu x]$
  其中 $\lambda, \mu \in \mathbb{R}$,$\mu \neq 0$,$P(x), Q(x)$ 为实系数多项式，最高次为 $m$ 次

二阶，$f(x)=P_{m}(x) e^{\lambda x}$型

令$y*=x^kQ_m(x)e^{\lambda x}$，
其中$Q_m(x)$是与$P_m(x)$同幂次的多项式，系数待定，$k$是$\lambda$作为微分方程的特征根的重数

• $\lambda$不是特征根：$k=0$
• $\lambda$是特征单根：$k=1$
• $\lambda$是二重特征根：$k=2$

上述结论可以推广到$n$阶：
令$y*=x^kQ_m(x)e^{\lambda x}$，$k$是$\lambda$作为$n$阶常系数线性微分方程的特征根的重数。

二阶，$f(x)=e^{\lambda x}\left[P_{m}(x) \cos \mu x+Q_{m}(x) \sin \mu x\right]$型

令$y^{*}=x^{k}\left[A_{m}(x) \cos \mu x+B_{m}(x) \sin \mu x\right] e^{\lambda x}$
其中$A_{m}(x), B_{m}(x)$均为$m$次待定多项式
若 $\lambda \pm i \mu$ 是方程的特征根，则取 k=1 ；若不是，则取 $k=0$

• 即使 $f$ 中 $P_{m}=0$ （或 $Q_{m}=0$ ），所设特解中仍应同时含 $\cos \mu x$ 和 $\sin \mu x$

上述结论可以推广到$n$阶：
$k$即是$\lambda \pm i \mu$作为$n$阶常系数线性微分方程的特征根的重数。

欧拉(Euler)方程

Euler方程：形如

$$x^{n} y^{(n)}+p_{1} x^{n-1} y^{(n-1)}+\cdots+p_{n-1} x y^{\prime}+p_{n} y=f(x)$$

的方程（其中 $p_{1}, p_{2}, \cdots, p_{n}$ 为常数）
解法：变量代换。令 $x=e^{t}$，则 $t=\ln x$

$n=2$ ：二阶Euler方程的形式为

$$x^{2} y^{\prime \prime}+p x y^{\prime}+q y=f(x) \text {. }$$

做变换 $x=e^{t}$ 后，可化为

$$\frac{d^{2} y}{d t^{2}}+(p-1) \frac{d y}{d t}+q y=f\left(e^{t}\right),$$

为一个二阶常系数线性非齐次微分方程。
特征方程为 $r^{2}+(p-1) r+q=0$