半导体物理笔记
本文最后更新于:2023年10月7日 上午
总结
第三章第四章总结
常用符号一览
| 符号 | 含义 | 重要关系式 |
|---|---|---|
| $E_c$ | 导带底的能量 | |
| $E_v$ | 价带顶的能量 | |
| $E_G$ | 带隙能量 | $E_G=E_c-E_v$ |
| $m^{*}$ | 有效质量 | $m^{*}=\left[\frac{\mathrm{d}^{2} E}{\mathrm{d} P^{2}}\right]^{-1}=\hbar^{2}\left[\frac{\mathrm{d}^{2} E}{\mathrm{d} k^{2}}\right]^{-1}$ |
| $g_{c/v}(E)$ | 态密度 | |
| $f(e)$ | 费米分布函数 | $f(E)=\frac{1}{1+e^{\left(E-E_{F}\right) / k T}}$ |
| $E_{F}$ | 费米能量/费米能级 | |
| $n/p$ | 电子/空穴数 | |
| $n_{i}/p_{i}$ | 本质半导体的电子/空穴数 | $p_{i}=n_{i}$ |
| $E_{i}$ | 本征半导体的费米能级 | $E_{i}=\frac{E_{c}+E_{v}}{2}+\frac{3 k T}{4} \ln \left(\frac{m_{p}^{*}}{m_{n}^{*}}\right) \cong \frac{E_{c}+E_{v}}{2}$ |
| $N_c$ | 未命名变量 | $N_{c}=2\left(\frac{m_{n}^{*} k T}{2 \pi \hbar^{2}}\right)^{3 / 2}$ |
| $N_v$ | 未命名变量 | $N_{v}=2\left(\frac{m_{p}^{*} k T}{2 \pi \hbar^{2}}\right)^{3 / 2}$ |
| $\tau$ | 散射时间 | |
| $\vec{v_d}$ | 漂移速度 | |
| $\mu$ | 载流子迁移率 | |
| $l$ | 平均自由程 | |
| $J_{p/n,\mathrm{drift}}$ | 漂移电流密度 | |
| $\sigma$ | 电导率 | |
| $\rho$ | 电阻率 | |
| $kT$ | / | $kT=0.026\mathrm{eV}$ |
第一章 固体物理初步
电阻率
- 导体:$\rho=10^{-5}-10^{-6} \Omega \cdot \mathrm{cm}$
- 绝缘体:$\rho=10^{14}-10^{18} \Omega \cdot \mathrm{cm}$
半导体:$\rho=10^{-3}-10^{3} \Omega \cdot \mathrm{cm}$
A semiconductor material has an electrical conductivity value falling between that of a metal (Cu, Au, etc.) and an insulator (glass etc.)
- The resistance of a semiconductor increases as the temperature decreases, which is the behavior opposite to that of a metal.
能带理论
能带论的基本出发点是认为固体中的电子不再是完全被束缚在某个原子周围,而是可以在整个固体中运动的,称之为共有化电子。但电子在运动过程中并也不像自由电子那样,完全不受任何力的作用,电子在运动过程中受到晶格原子势场的作用。
能带论的两个基本假设
Born-Oppenhaimer 近似(玻恩-奥本海默绝热近似)
所有原子核都周期性地静止排列在其格点位置上,因而忽略了电子与质子的碰撞。
Hatree-Fock平均场近似
忽略电子与电子间的相互作用,用平均场代替电子与电子间的相互作用。即假设每个电子所处的势场完全相同,电子的势能只与该电子的位置有关,而与其他电子的位置无关。
能级与能带
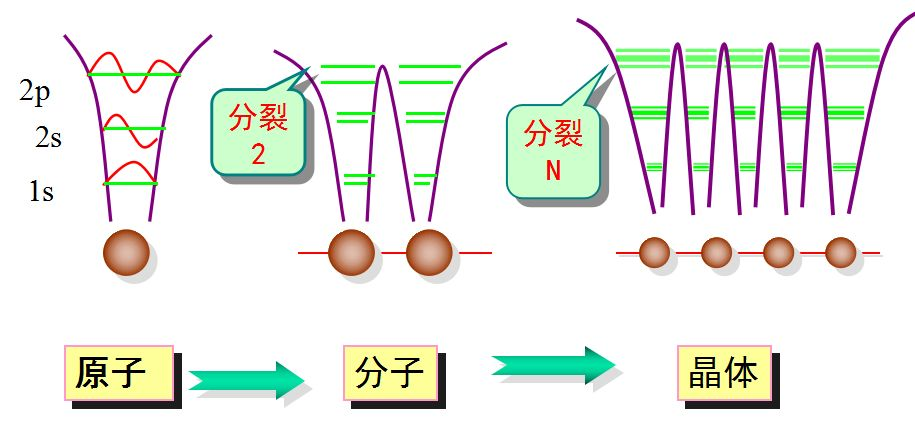
当两个相同的原子相互靠近的时候,会出现这样一个矛盾:两个电子一模一样,所以它们的运动状态和轨道肯定也是一模一样,但是这与泡利不相容原理矛盾,因此当发生电子共有化运动的时候,这两个一模一样的电子会出现细微的差别,主要表现在电子轨道不同,一个电子的轨道会比另一个电子轨道略高或者略低,就出现了两个不同的能级,这就是能级分化/扩展成能带。
- 当能级分化时,能量大的电子便可以到处串门,便成了所有原子的“共有电子”
- 这些共有电子都可以在整个固体(晶体)中自由自在地跑来跑去,我们将它们叫做自由电子。自由电子的存在决定了固体的导电性能。
- 如果固体中总的原子数目为N的话,原来的一个能级就分裂成了N个能级。
- 原子能级的分裂与原子之间的距离有关。当原子之间相距很远时,每个原子相当于单原子,电子处于相同的单原子的能级上。如果原子之间距离越来越近,单个原子的电子逐渐公有化,能级分裂成许多相隔很近、貌似连续的能级,形成能带。
导带
价带之上的第一个,即能量最低的那个允许电子占有的能带叫导带
价带
价电子(原子核外电子中能与其他原子相互作用形成化学键的电子)的能级分裂而形成的能带叫价带
禁带
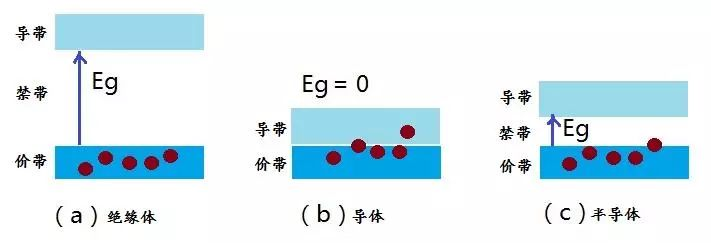
导带和价带之间可以有空隙,称之为能隙,或禁带。对于不同的材料,禁带宽度不同,导带中电子的数目也不同,从而有不同的导电性。导带、价带和禁带之间的关系决定了绝缘体、导体、半导体的区别。
- 绝缘体的价带充满电子,导带是空带,导带和价带之间有很宽的能隙(禁带),价带中的电子很难突破这个禁带到达导带,所以,绝缘体不能导电。
- 导体中没有禁带,导带和价带连在一起,甚至互相重叠,价带中的电子可以到达导带而成为整个固体共有的自由电子,所以,导体有强导电性。
- 半导体的价带也是满带,但是价带和空带之间的能隙很小,也可能有交叠。这样它就很容易在外界作用(如光照、升温等)下发生跃迁而发生导电现象。但它的导电性能比导体要差得多,因而称之为半导体。
| 材料 | Ge | Si | GaAs | GaN | 金刚石 |
|---|---|---|---|---|---|
| 带隙宽度(室温) | 0.66eV | 1.12 eV | 1.42 eV | 3.44 eV | 5.47 eV |
传统半导体材料与应用
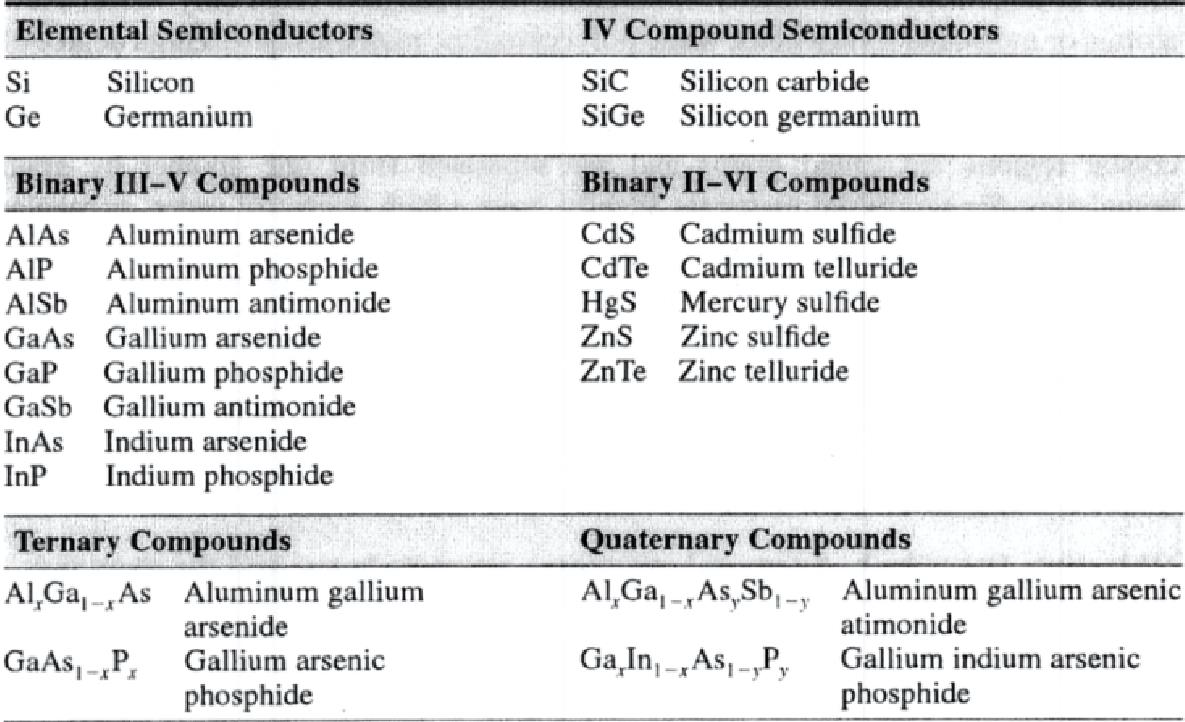

新型半导体材料
略
二维半导体材料
一维半导体材料
纳米线
碳纳米管
零维半导体材料
量子点
固体材料分类
非晶
不具有规则的几何构型的物质为非晶体。
例如非晶硅,可用于太阳能板、红外探测。
单晶
整块物质都由原子或分子按一定规律作周期性重复排列的晶体称为单晶体
例如单晶硅,用于IC芯片
多晶
整个物体是由许多杂乱无章的排列着的小晶体组成的,这样的物体叫多晶体。
例如多晶硅,用于MOSFET、大规模光伏
晶体相关定义
晶格
晶胞
单胞
初基原胞
基元:一个理想的晶体是由完全相同的原子团(或分子、原子)— 基本结构单元,在空间周期性重复排列而成的。构成晶体的完全相同的基本结构单元,称为基元。基元可以是一个原子(金、银、铜),两个以上原子(石墨、金刚石),无机晶体可达100,化合物1000,蛋白质10000。任何两个基元中相应原子周围的情况是完全相同的(几何环境、化学性质);而每一个基元中不同原子周围情况则不相同。原胞:以三个基矢为边长形成的平行六面体,称为原胞(固体物理学原胞,初级原胞)。 代表原胞三个边的矢量即为原胞的基矢。晶胞(结晶学原胞,布拉维原胞,单胞):使三个基矢的方向尽可能地沿着对称轴的方向,它具有明显的对称性。
常见晶体结构
简单立方晶体(Simple cubic crystal,SC)
体心立方晶格(Body centered cubic crystal,BCC)
体心立方晶格的晶胞中,八个原子处于立方体的角上,一个原子处于立方体的中心,角上八个原子与中心原子紧靠。
三维最密堆积
ABC方式与AB方式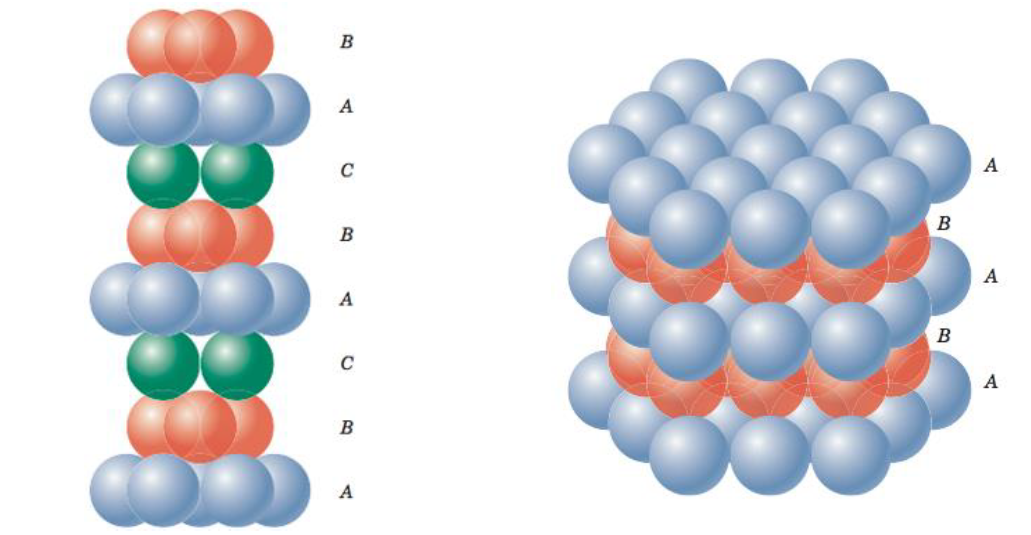
六方最密堆积(Hexagonal close packed crystal,HCP)
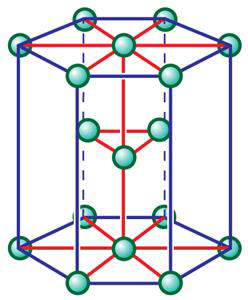
面心立方晶格(Face-centered cubic crystal,FCC)
面心立方晶格的晶胞是一个立方体,立方体的八个顶角和六个面的中心各有一个原子。
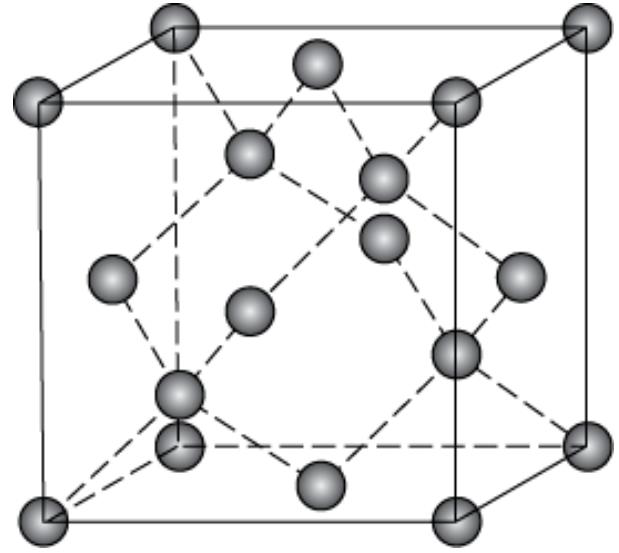
金刚石结构(Diamond structure)
在晶体学中,金刚石结构又称为金刚石立方晶体结构,原型是金刚石。金刚石结构中的每个原子与相邻的 4 个原子形成正四面体,故单胞内原子数为 5。具有金刚石结构的晶体除了金刚石以外,还有硅、锗、α-锡等。
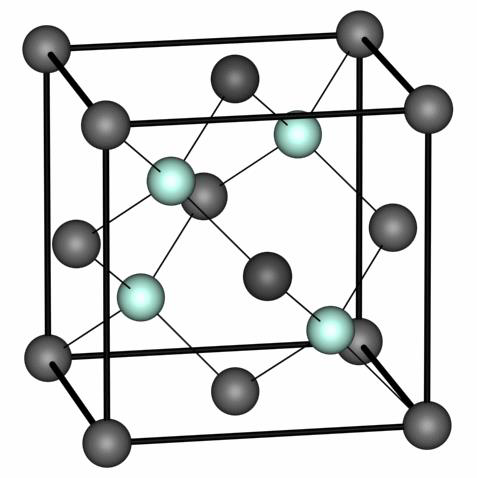
闪锌矿结构(Diamond structure)
闪锌矿结构以硫化锌晶体为代表的一类化合物晶体的结构。由两种元素的原子各自形成面心立方晶格再沿对角线滑移对角线长度的四分之一套迭而成。
晶格因子/参数(Lattice Factors)
原胞
晶体的原胞是构成晶体的周期性结构单元,但是原胞往往由于太小而不能反映晶格的对称性。有的晶体,无论怎样选取原胞,都不能直接反映出整个格子的对称性。体心和面心立方晶体就是这种情形。为了反映格子的对称性,必须选取较大的周期单元。
- 体心立方结构和面心立方结构的原胞都是一个不具有立方对称性的平行六面体
单胞(Unit cell)
在能够保持晶格对称性的前提下,构成晶体的周期性结构单元称为晶体的单胞。单胞的边矢量称为单胞基矢,通常用 $a,b,c$ 表示
- 体心立方结构和面心立方结构的单胞为体心立方体和面心立方体;
- 单胞有时称为晶胞、惯用原胞(结晶学中惯用)
初基元胞(primitive cell)
初基元胞是在能够保持晶格对称性的前提下,构成晶体的最小周期性结构单元。
晶格常数(Length of the cell edge)
单胞的边长称为晶格常数
配位数(Coordination Number)
配位数是晶格中与某一布拉维晶格相距最近的格子个数。
单胞原子数(Number of atom per unit cell)
一个单胞中的原子数
密排指数(Atomic Packing Factor)
APF = 组成颗粒占据的体积分数
常见堆积的参数
晶向
晶向是指晶体的一个基本特点是具有方向性,沿晶格的不同方向晶体性质不同。布拉维点阵的格点可以看成分列在一系列相互平行的直线系上,这些直线系称为晶列。同一个格点可以形成方向不同的晶列,每一个晶列定义了一个方向,称为晶向。
- 晶体中的一个特定方向可以表示为一组三个互质整数,它们是该方向上的一个矢量的分量。标志晶向的这一组数称为晶向指数。
- 晶向指数依次放在方括号
[]内,负号用上标 $\bar{x}$ 表示。 - 对于立方系,晶向 $[100]$、$[010]$、$[001]$ 及其相反晶向就可以用 $<100>$ 表示,其它晶系不适用。
晶面
晶面是在晶体中由原子、离子或分子的阵点所组成的平面。晶体可看成是由一层层晶面堆砌而成。
设 $a,b,c$ 为晶体的一套基向量,晶面在 $a,b,c$ 上所截长度分别为 $pa,qb,sc$,则 $p,q,s$ 为晶面在三个晶轴上的截数,而 $1/p,1/q,1/s$ 为倒易截数。将晶面在三个晶轴上倒易截数之比化为一组互质整数,即 $1/p:1/q:1/s=h:k:l$,则这一套互质整数即为晶面指标,也叫密勒指数,用 $(hkl)$ 符号来表示。
第二章 量子力学初步
波粒二象性(Wave Particle Duality)
略
双缝干涉(Double slit experiment)
略
光电效应(Photoelectric effect)
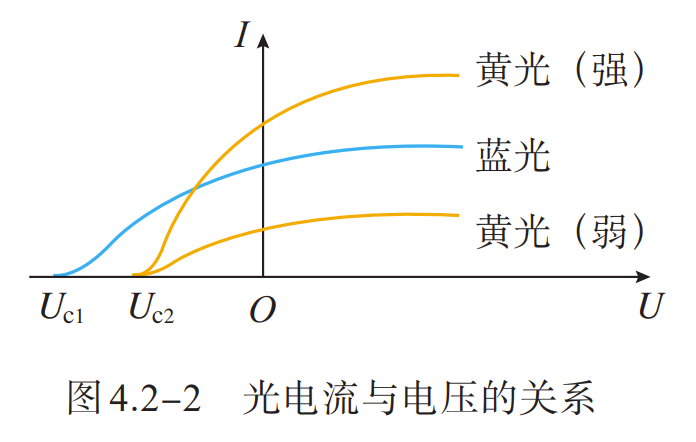
- 光电效应是物理学中一个重要而神奇的现象。在高于某特定频率的电磁波(该频率称为极限频率,threshold frequency)照射下,某些物质内部的电子吸收能量后逸出而形成电流,即光生电。
- 只要光的频率超过某一极限频率,受光照射的金属表面立即就会逸出光电子,发生光电效应。当在金属外面加一个闭合电路,加上正向电源,这些逸出的光电子全部到达阳极便形成所谓的光电流。
- 在入射光一定时,增大光电管两极的正向电压,提高光电子的动能,光电流会随之增大。但光电流不会无限增大,要受到光电子数量的约束,有一个最大值,这个值就是饱和电流。
- 当入射光强度增大时,单位时间里通过金属表面的光子数也就增多,于是,光子与金属中的电子碰撞次数也增多,因而单位时间里从金属表面逸出的光电子也增多,电流也随之增大;光电子最大动能不变。
- 当入射光频率增加时,光电子最大动能增加。
物质波(Matter Wave)
德布罗意提出假设:实物粒子也具有波动性,即每一个运动的粒子都与一个对应的波相联系。粒子的能量 $\varepsilon$ 和动量 $p$ 跟它所对应的波的频率 $\nu$ 和波长 $\lambda$ 之间,遵从如下关系:
其中
- $k=\frac{2\pi}{\lambda}$ 为波矢
- $h=6.63\times 10^{-34} \mathrm{J}\cdot \mathrm{s}$ 为普朗克常量
- $\hbar=h/2\pi=1.05\times 10^{-34} \mathrm{J}\cdot \mathrm{s}$ 为约化普朗克常量
海森堡测不准原理
波函数
- 波函数 $\Psi(x, t)$ 一个复值的概率幅度,它是对一个孤立的量子系统的量子状态的数学描述。
- 波函数是一个复值函数
- 波函数模的平方 $|\Psi(x, t)|^2$ 描述在时间t找到 $x$ 和 $x+\mathrm{d}x$ 之间的粒子的概率
- 标准化方程:
薛定谔方程
一维时变形式
一维不含时形式(定态)
其中 $V(x)$ 表示一维空间中的势场分布。
自由电子求解(V(x)=0)
- 其中 $k=\sqrt{\frac{2 m E}{\hbar^{2}}}$
- 指数形式对应行波,用于非束缚态边界问题
- 三角函数形式对应驻波,用于束缚态边界问题
- 完整形式为
势垒&势井
无限深势井
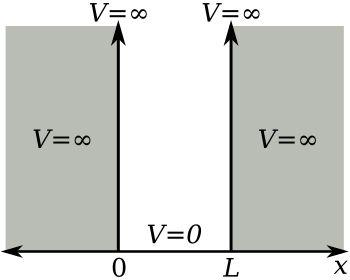
其中 $k=\sqrt{\frac{2 m E}{\hbar^{2}}}$
代入边界条件和归一化条件:
解得
阶梯势垒
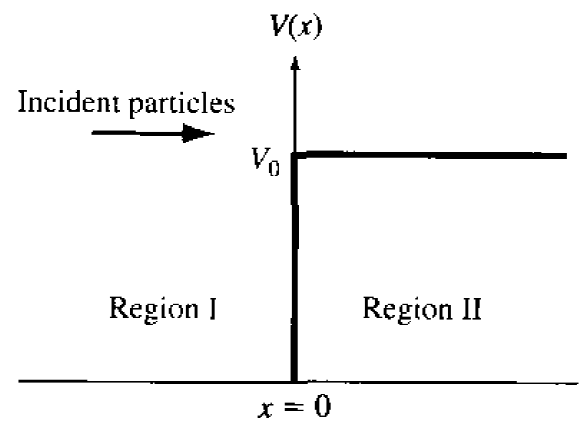
区域一:
其中
区域二:
其中
边界条件:
解得
定义反射率与透射率
阶梯势垒的反射率为 $1$,透射率不为 $0$。
方形势垒

在I、III区
其中
在II区
其中
边界条件
透射率
玻尔电子模型
- 经典玻尔理论: 原子核是一个带正电的重质子,电子是一个带负电的轻粒子,它围绕原子核旋转。
- 电子与原子核的势能方程:
- 电子的角动量可以被量子化
- 量子化的能量:其中
- 电子质量
- 电子电量
- 真空介电常量
量子力学解释电子模型
解得
其中
- 主量子数 $n=1,2,3,\cdots$,即电子层数
- 角量子数 $l=n-1,n-2,\cdots,0$,表示电子的亚层或能级
- 磁量子数 $m=\pm l,\pm (l-1),\cdots,0$,代表每个亚层的轨道(轨道方向)
对于 $n=1$,波函数为
第三章 载流子模型与特性
能带模型

- 在简化模型中,导带底的能量记为 $E_c$,价带顶的能量记为 $E_v$,带隙能量为 $E_G=E_c-E_v$
- 空穴占据导带,电子占据价带
- $E_G$ 就是电子刚好跃迁到导带要吸收的能量
- 绝缘体的 $E_G$ 很大,半导体的 $E_G$ 较小,导体的 $E_G$ 是负数
- 传统半导体材料的带隙能量
| 材料 | Ge | Si | GaAs |
|---|---|---|---|
| 能量($\mathrm{eV}$) | $0.67$ | $1.12$ | $1.42$ |
E-k关系
自由电子
由薛定谔方程求解可得
图像是二次曲线
一维晶格周期势下
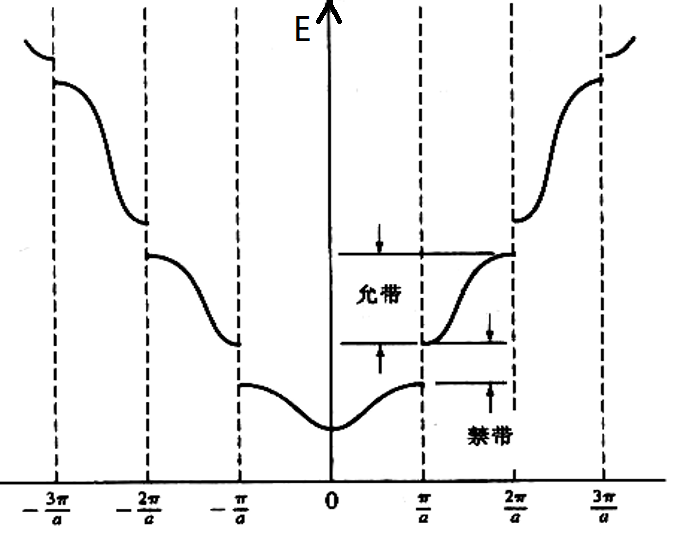
由于周期分布,把曲线都集中到 $[-\frac{\pi}{a},\frac{\pi}{a}]$ 里

直接带隙半导体和间接带隙半导体
- 直接带隙半导体材料就是导带最小值(导带底)和满带最大值在k空间中同一位置,电子要跃迁到导带上产生导电的电子和空穴(形成半满能带)只需要吸收能量
- 间接带隙半导体材料导带最小值(导带底)和满带最大值在k空间中不同位置,形成半满能带不只需要吸收能量,还要改变动量

有效质量
晶格中的电子受到原子核的周期性势场以及其他电子势场综合作用,将这些力看成内力,可以引进有效质量的概念,它概括了半导体内部势场的作用,使得在解决半导体中电子在外力作用下的运动规律时,可以不涉及半导体内部势场的作用。
- 其中 $P=\hbar k$
- 导带底电子有效质量为正,价带顶电子有效质量为负
- 温度为 300K 时的有效质量
| 材料 | $m_n^{*}/m_0$ | $m_p^{*}/m_0$ |
|---|---|---|
| Si | 1.18 | 0.81 |
| Ge | 0.55 | 0.36 |
| GaAs | 0.066 | 0.52 |
掺杂
- 施主原子:P,As,Sb(N型掺杂)
- 受主原子:B,Al,Ga,In(P型掺杂)
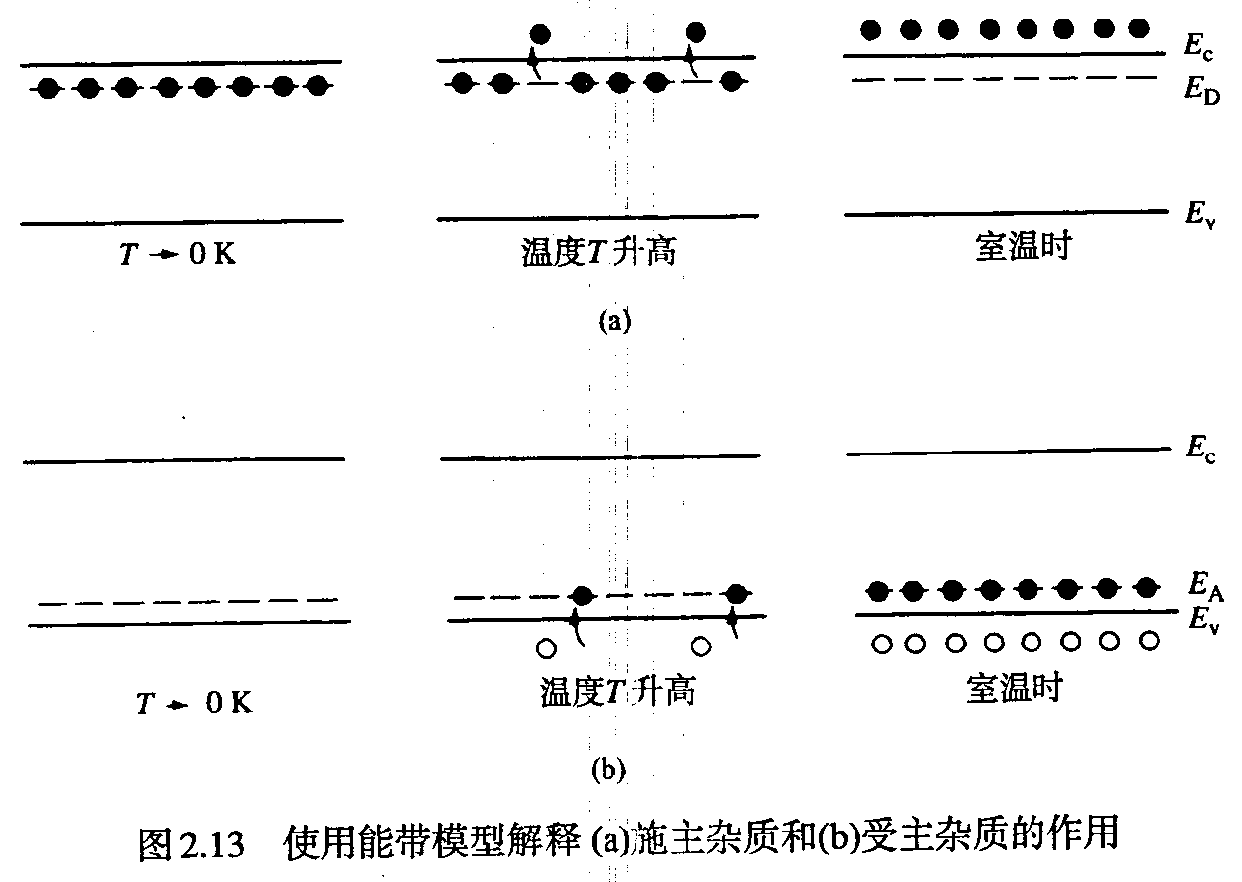
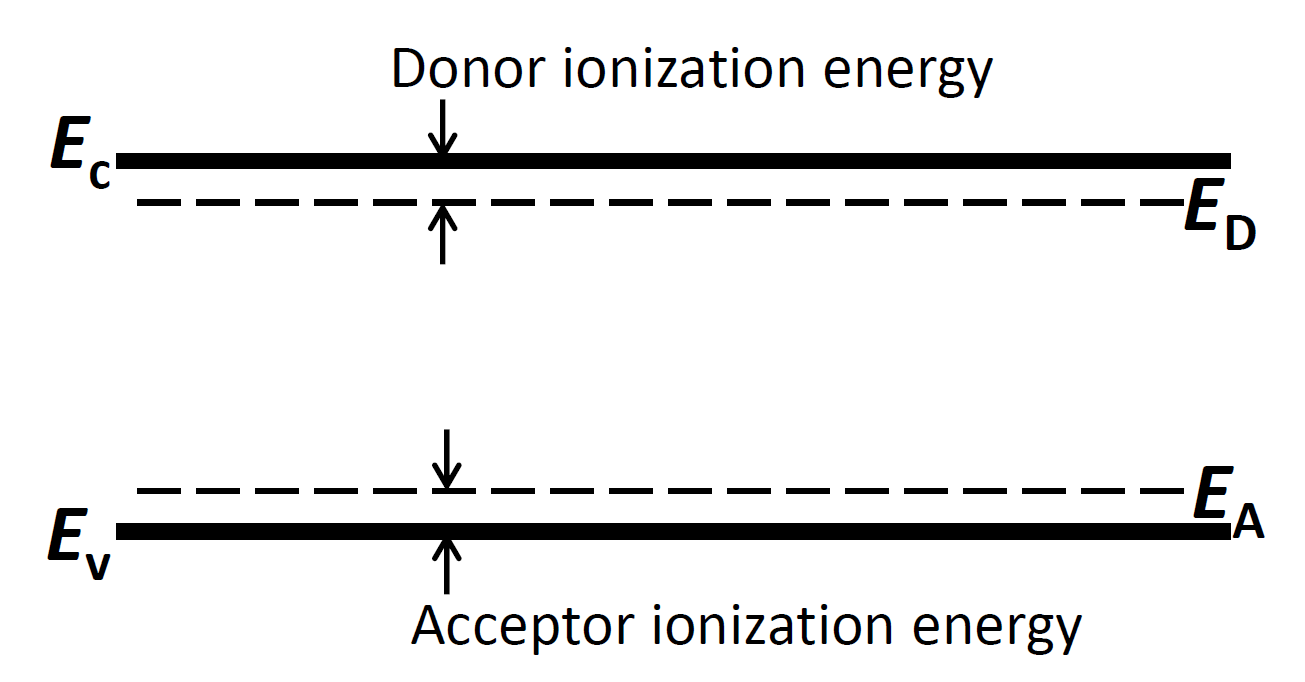
| 施主 | 受主 | |||||
|---|---|---|---|---|---|---|
| 掺杂原子 | Sb | P | As | B | Al | In |
| 电离能(meV) | 39 | 45 | 54 | 45 | 67 | 160 |
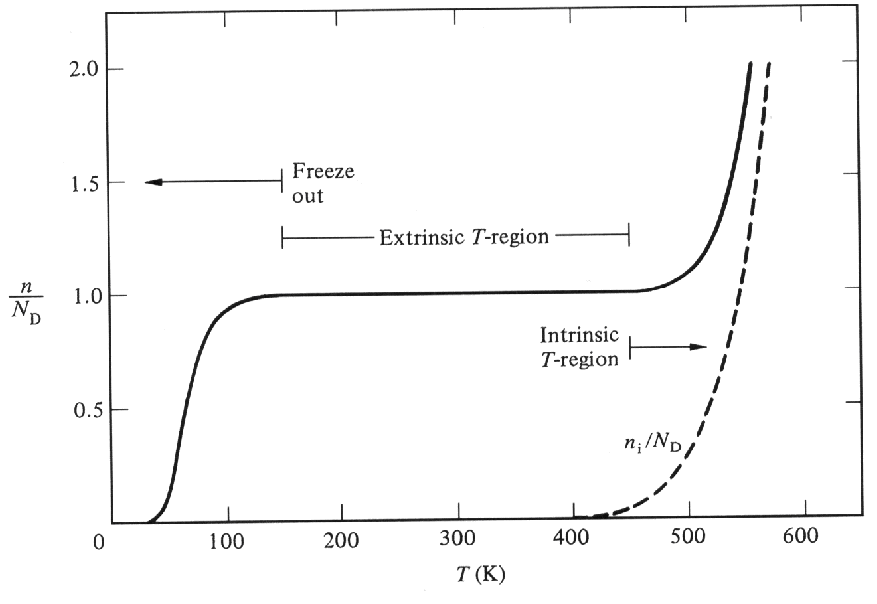
电离电子随温度变化图
态密度
- 概念:每立方厘米所含量子态的数目分布
- 在能带边缘附近:
费米分布函数
- 费米分布函数是热平衡体系中粒子按能量分布的一种规律,表示一个电子占据能量为 $E$ 的本征态的几率。
- 其中 $E_{F}$ 称为费米能量/费米能级,刚好是被占据概率为 50% 的能级

- n型掺杂的 $E_{F}$ 增大,积分可得体系里的自由电子更多
- p型掺杂的 $E_{F}$ 减小,积分可得体系里的自由空穴更多
玻尔兹曼近似
- 物理解释:玻尔兹曼近似适用于轻掺杂的情况,此时可以忽略电子之间的相互作用
费米分布函数积分
导带所有电子数:(n型掺杂)
使用玻尔兹曼近似:
价带所有空穴数:(p型掺杂)
使用玻尔兹曼近似:
本质半导体:
- 本征载流子浓度取决于温度、带隙和载流子有效质量
- 温度越高,$n_i$ 越大;带隙越大,$n_i$ 越小
- 对于硅材料,在 300K 时,$n_i=10^{10}\mathrm{cm}^{-3}$
电荷守恒
其中
- $N_D^{+}$ 是电离的施主原子数
- $N_A^{-}$ 是电离的受主原子数
- $N_D$ 是完全电离的施主原子数
- $N_A$ 是完全电离的受主原子数
在掺杂原子完全电离的情况下,可以用掺杂原子浓度和本征载流子浓度来表示 $n$ 和 $p$
- 对于本征半导体
- 对于 N 型半导体
- 对于 P 型半导体
- 在高温下
- 对于补偿半导体
本征半导体的 $E_F$
于是可以用 $n_i$ 来表示 $n,p$
也就是说
当温度在 300K 时,又有
第四章 载流子的输运
基本概念
- 漂移
- 扩散
有效质量
| Si | Ge | GaAs | |
|---|---|---|---|
| $m_n^{*}/m_0$ | 0.26 | 0.12 | 0.068 |
| $m_p^{*}/m_0$ | 0.39 | 0.30 | 0.50 |
零电场时载流子的平均动能
对于硅,
非零电场时载流子的运动
- 散射时间 $\tau$:两次散射发生的平均时间间隔
- 漂移速度 $\vec{v_d}=-\frac{q\tau}{m^{*}}\vec{E}$
- 载流子迁移率 $\mu=q\tau/m^{*}$
- 平均自由程 $l=v_{th}\tau$
载流子迁移率是指载流子(电子和空穴)在单位电场作用下的平均漂移速度
| Si | Ge | GaAs | InAs | Graphene | |
|---|---|---|---|---|---|
| $\mu_n\ (\mathrm{cm}^2/\mathrm{V}\cdot\mathrm{s})$ | 1400 | 3900 | 8500 | 30000 | 140000 |
| $\mu_p\ (\mathrm{cm}^2/\mathrm{V}\cdot\mathrm{s})$ | 470 | 1900 | 400 | 500 | 140000 |
常见散射模式
- 低电场:掺杂离子散射、声子散射
- 高电场:光学声子散射
- 轻掺杂:晶格散射主导
- 重掺杂:杂质离子散射主导
- 超重掺杂:载流子间相互作用主导
- 其他:不均匀等
掺杂离子散射的迁移率
温度越高迁移率越高,浓度越大迁移率越低
晶格振动散射的迁移率
马西森定则
迁移率与温度
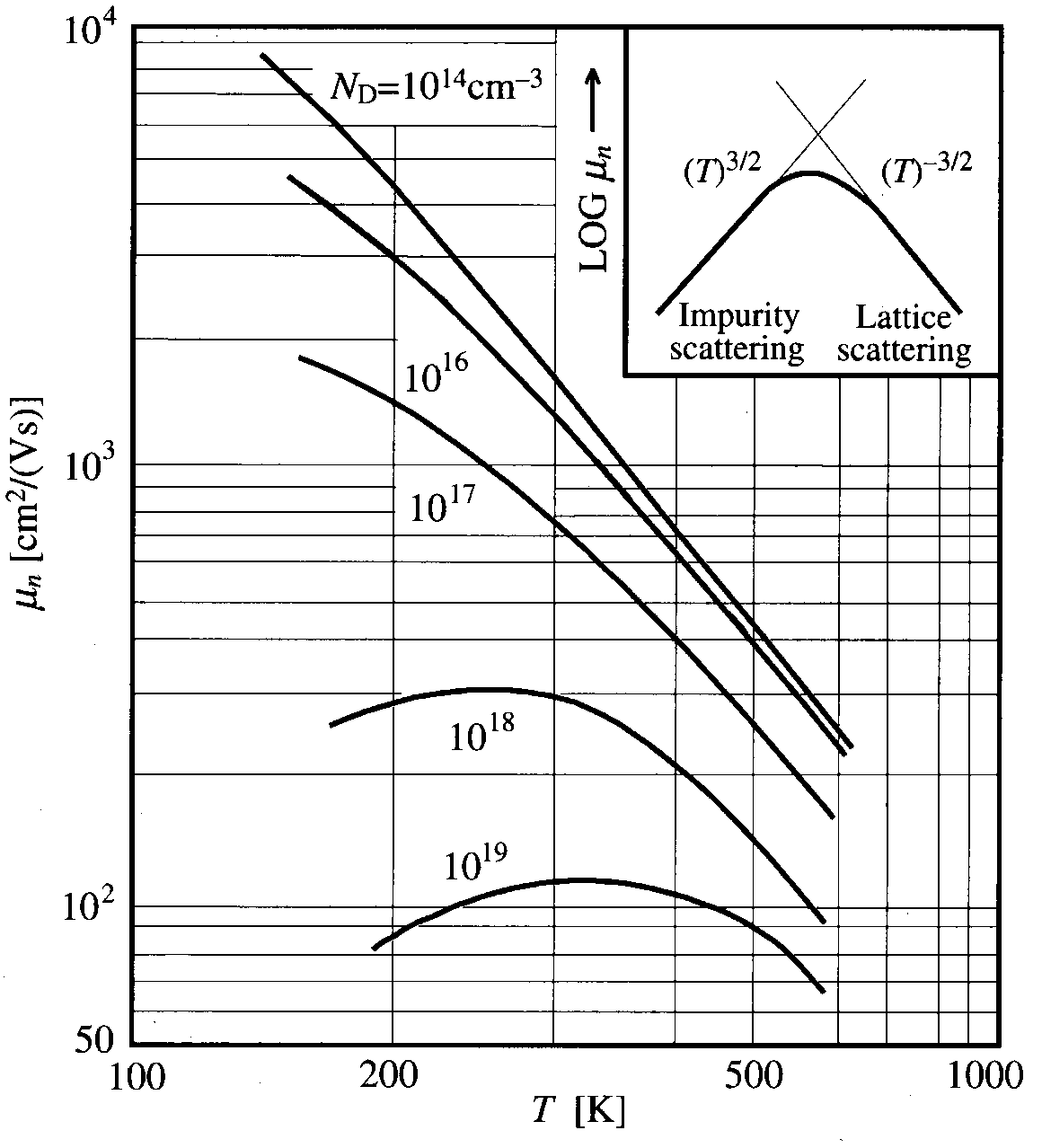
漂移电流密度
定义电导率
- 迁移率是描述单个载流子的运动快慢,而电导率是整体的所有载流子的导电性能
定义电阻率
则有欧姆定律
欧姆定律微观形式
掺杂硅的电阻率
能带模型解释载流子输运
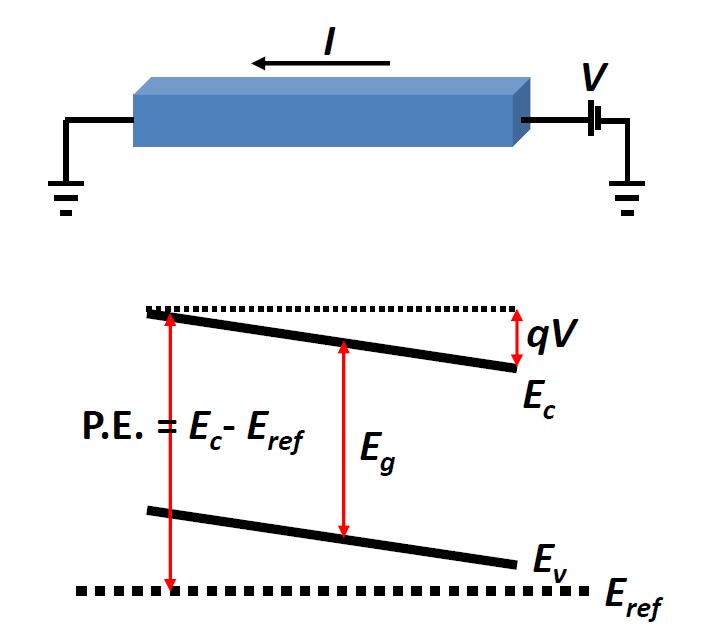
直观解释:载流子受到电场力作用向右运动并获得动能,偏离导带底部,然后遇到散射,又回到导带底部,如此循环往复。
测量电阻
二探针法
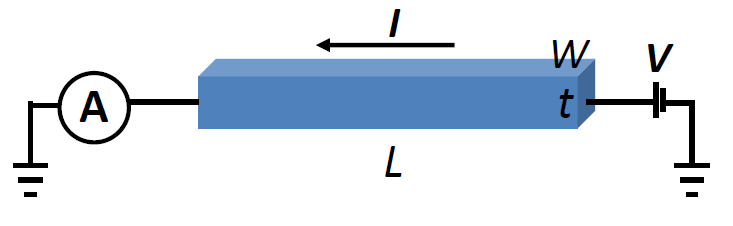
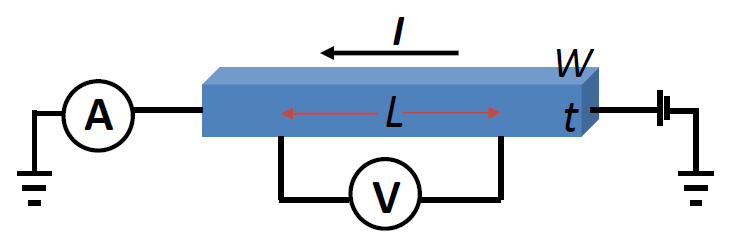
四探针法
圆盘
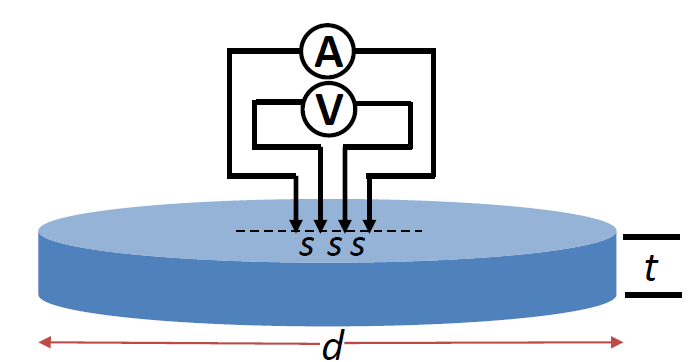
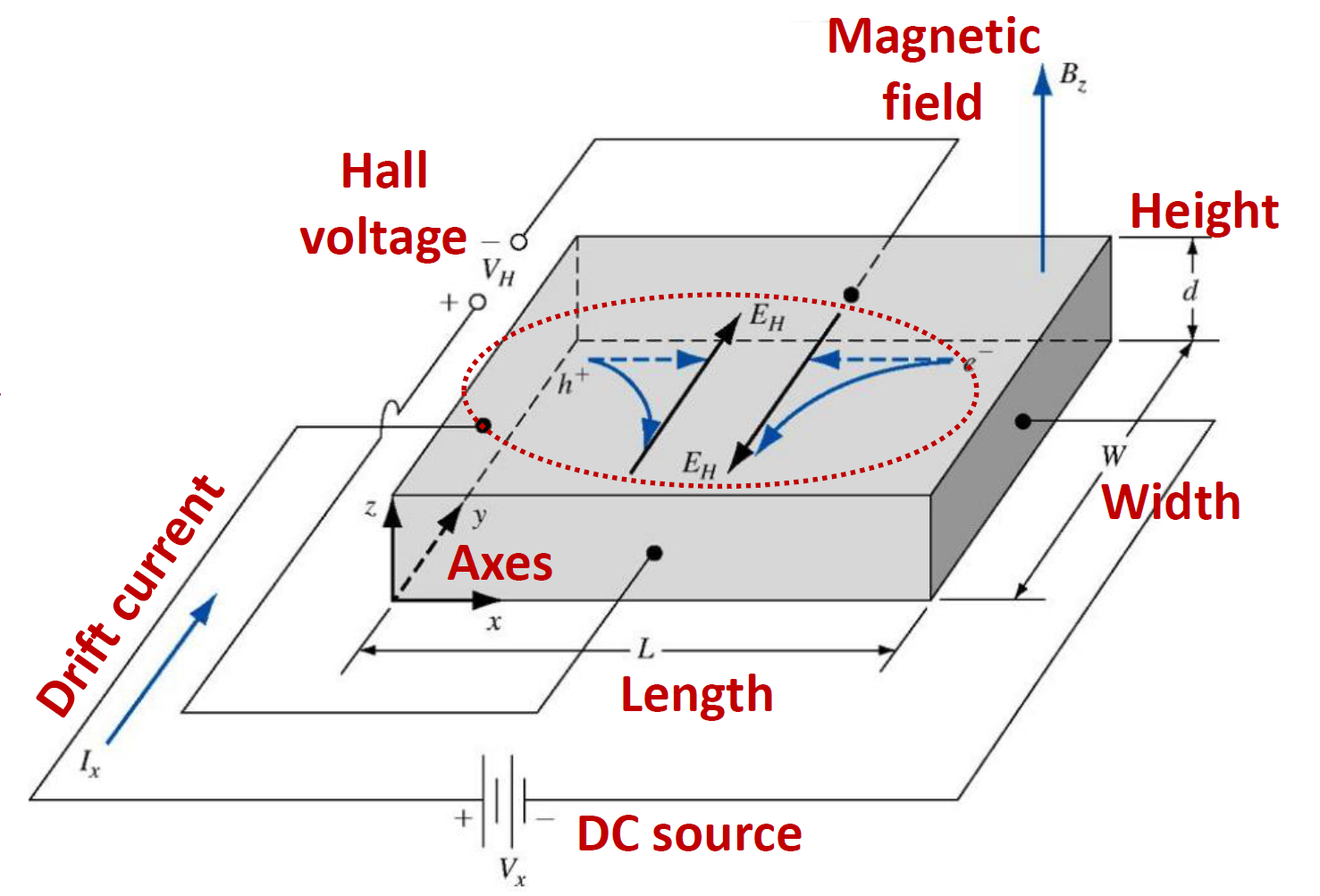
霍尔效应
场效应管
其中 $C_i$ 是单位面积栅极介电电容
菲克第一定律(载流子扩散电流)
其中 $D$ 是扩散常数(扩散率)
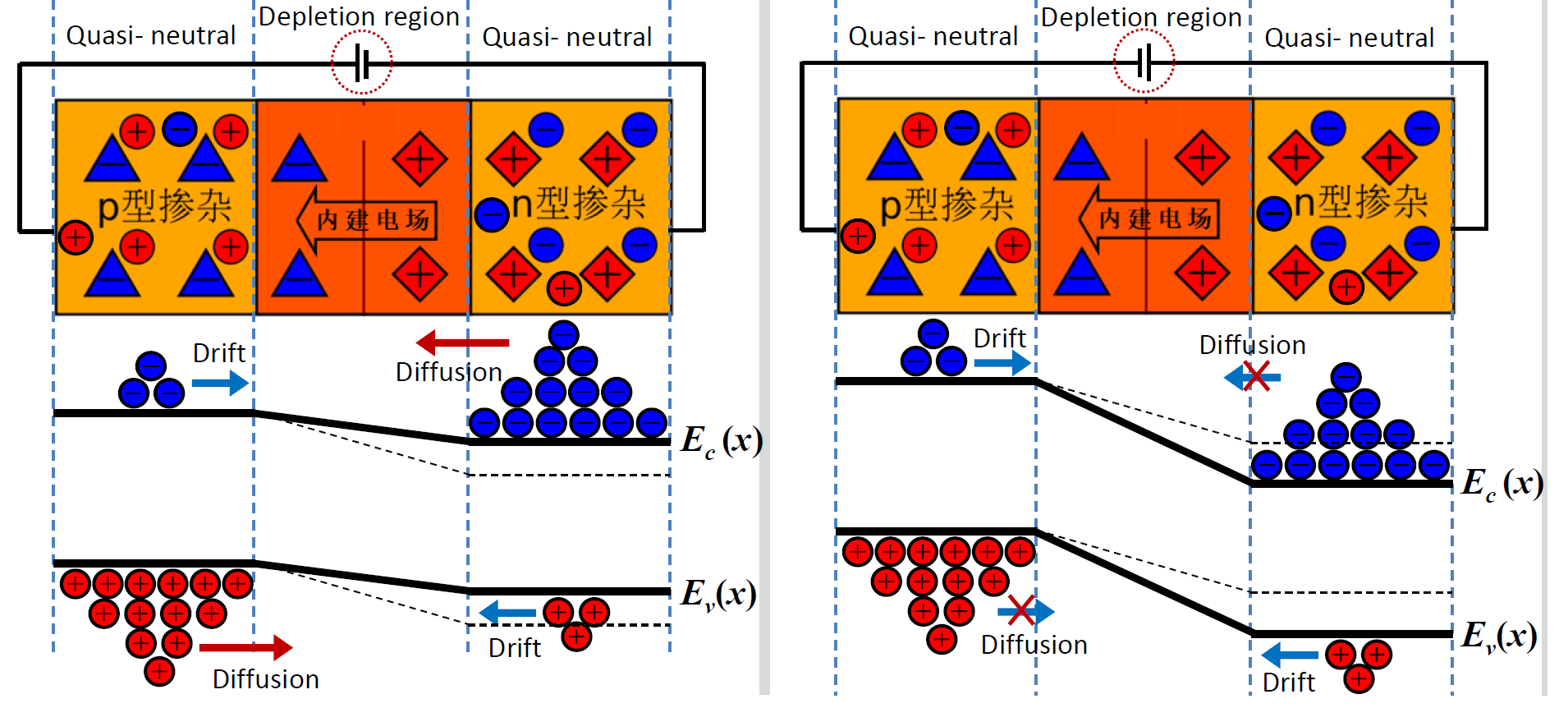
非均匀掺杂半导体
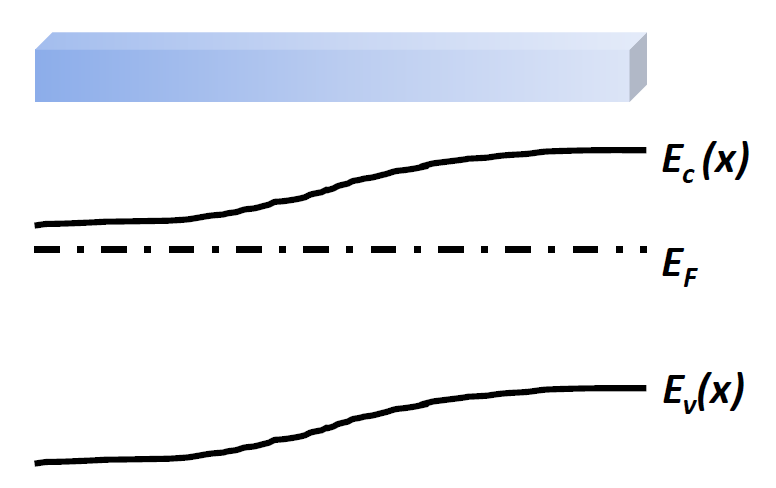
- 非均匀掺杂半导体内部存在扩散电流和漂移电流,两者代数和为0
- 以n型半导体为例,电子从浓度高的一侧扩散到浓度低的一侧,导致浓度高的一侧用大量正离子,内部就产生电场。电场阻止电子继续扩散。
- 在电场作用下,载流子的定向运动,即空穴沿着电场方向的运动,电子逆着电场方向的运动统称为漂移运动。由于热运动而使载流子从高浓度区域向低浓度区域的流动称为扩散运动。描述载流子漂移运动特征的物理量是“迁移率”,描述载流子扩散运动特征的物理量是“扩散系数”
- 内建电场电势差
- 内建电场强度
爱因斯坦关系
对于热平衡状态的半导体没有净电流流动
根据电流密度的定义
把电场强度代入,得
爱因斯坦关系把载流子的扩散系数和迁移率关联起来,爱因斯坦关系在非简并掺杂和非热平衡状态都适用。
电子空穴对
- 产生:电子和空穴成对产生
- 复合:电子和空穴成对湮灭
- 过剩载流子:在非热平衡状态下产生的多余的电子空穴对
- 载流子注入:改变外部条件产生过剩载流子的过程
- 当受到干扰时,系统倾向于恢复平衡。
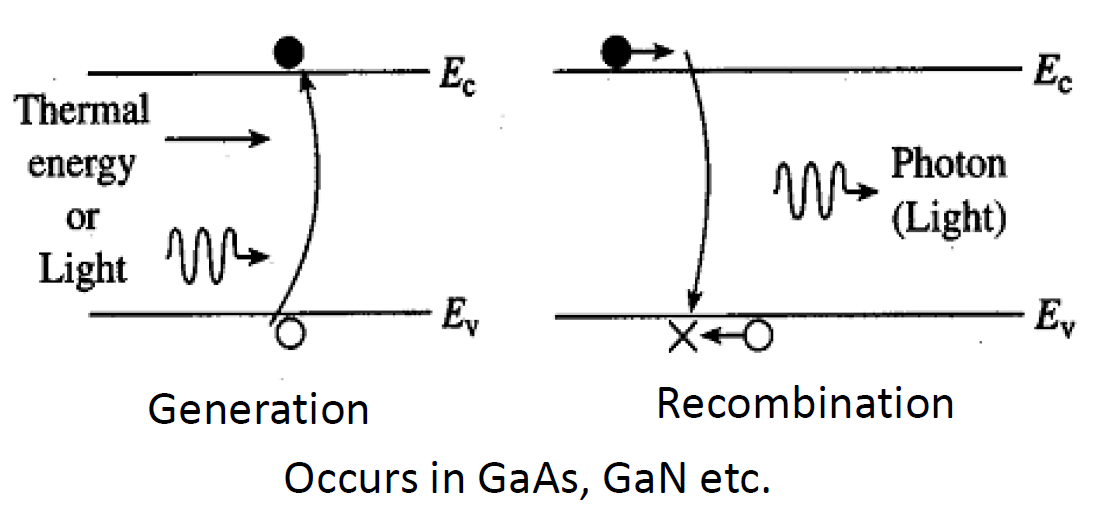
- 复合过程中释放的能量可用于发射光子(辐射性复合)或作为热量散失到晶格中(非辐射性复合)。
- 带到带过程:
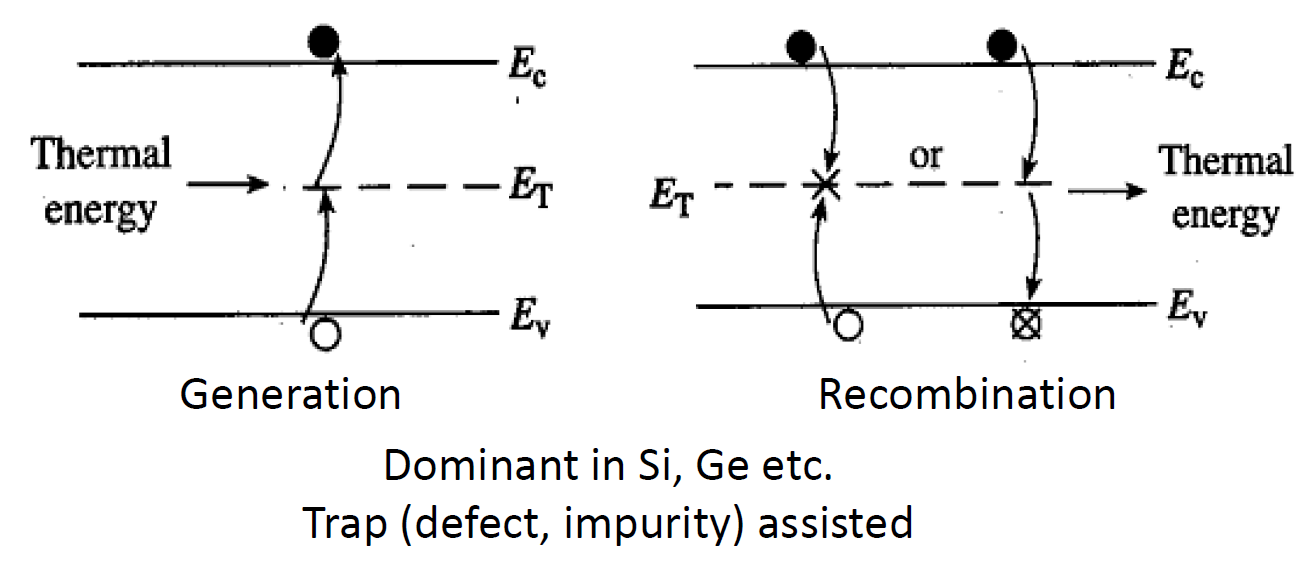
- 复合产生中心过程:
- 载流子-载流子相互作用过程:

- 碰撞离化:是指半导体中的自由载流子在强电场作用下加速到具有足够高的能量,在与晶格的相互作用中使另一个电子从价带跃迁到导带,从而产生新的电子-空穴对的过程。载流子在强电场区内的一连串碰撞离化过程造成载流子的雪崩倍增,在外电路中表现为电流的雪崩倍增。
- 俄歇效应:俄歇效应是原子发射的一个电子导致另一个或多个电子(俄歇电子)被发射出来而非辐射X射线,使原子、分子成为高阶离子的物理现象,是伴随一个电子能量降低的同时,另一个(或多个)电子能量增高的跃迁过程。
小注入
多子浓度不变,少子浓度显著改变
小注入半导体空穴间接复合率、产生率
非热平衡状态空穴的复合率
其中 $c_{p}$ 为空穴俘获系数,$N_T$ 为单位体积内 R-G 中心数量。小注入条件下空穴的产生率
空穴的净变化率
令
则空穴和电子的净变化率
少子寿命
少数载流子寿命是过量少数载流子在多数载流子海洋中“存活”的平均时间。$\tau$ 在硅中的范围从 1ns 到 1ms,并取决于金属杂质(污染物)的密度,如金和铂,以及晶体缺陷的密度。这些杂质/缺陷在带隙深处产生了局部的能量状态。这种深层陷阱捕获电子或空穴以促进重组,被称为重组生成中心。
一般情况下的载流子变化率
载流子连续性方程
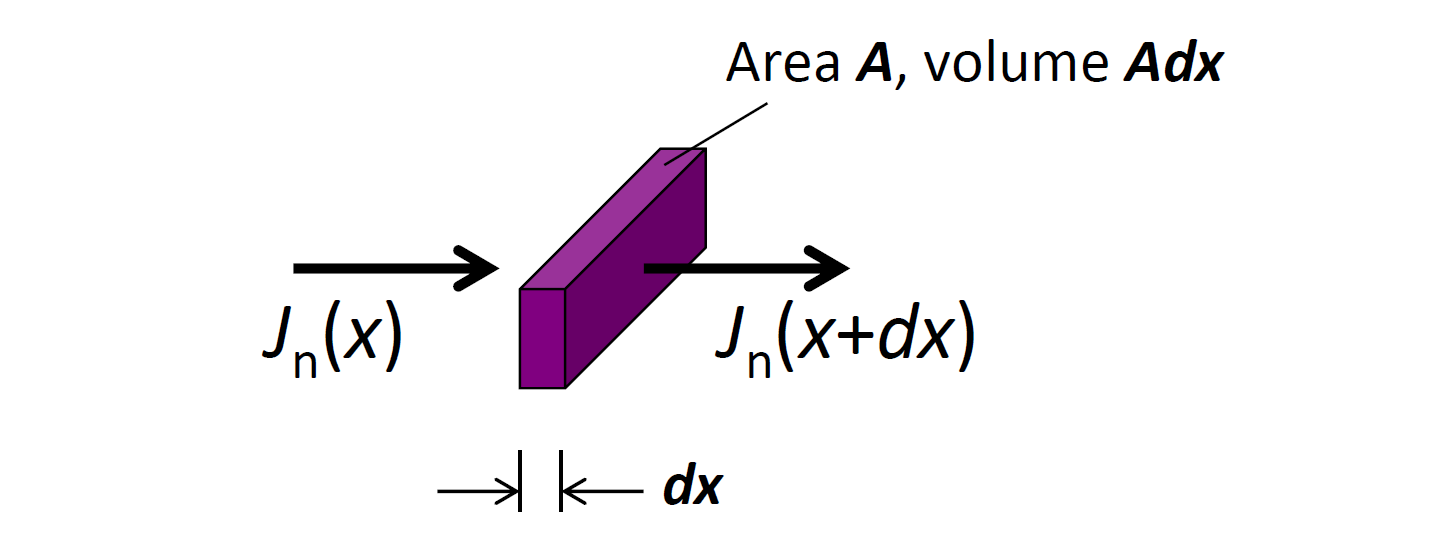
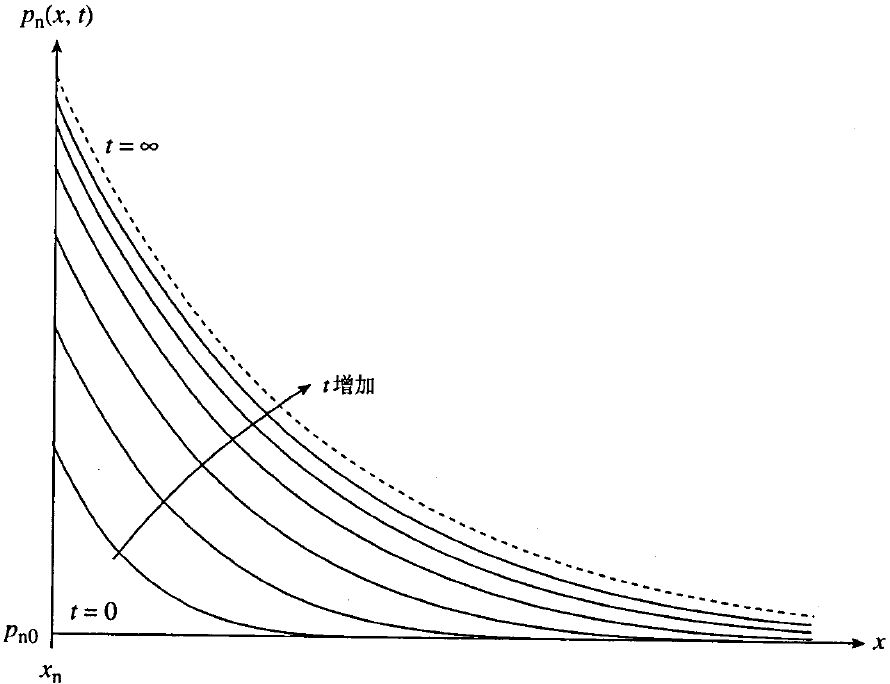
解得
少子扩散方程
若假设
- 电场强度较小
- 连续性掺杂
- 小注入
则可化简为 - 若稳态:$\frac{\partial \Delta n_{p}}{\partial t}=0 \quad \frac{\partial \Delta p_{n}}{\partial t}=0$
- 若无扩散电流:$D_{n} \frac{\partial^{2} \Delta n_{p}}{\partial x^{2}}=0 \quad D_{p} \frac{\partial^{2} \Delta p_{n}}{\partial x^{2}}=0$
- 若无 R-G 中心过程:$\frac{\Delta n_{p}}{\tau_{n}}=0 \quad \frac{\Delta p_{n}}{\tau_{p}}=0$
- 若无光照:$G_{L}=0$
扩散长度
在物理意义上,$L_p$ 和 $L_n$ 代表了少数载流子在被湮灭之前扩散到多数载流子海洋中的平均距离。
准费米能级
当半导体存在载流子注入时,$np=n_i^2$ 不再成立,但是我们仍然有
这里的 $F_{N}$ 和 $F_{P}$ 被称为准费米能级
其他载流子输运过程
俄歇效应&碰撞离化
热离子发射
量子隧穿
弹道输运
- 在介观物理学中,弹道传导是指 电荷载流子在介质中的传输,具有可忽略不计的 由散射引起的电阻率。
- 当电子的平均自由路径电子的平均自由路径比介质的尺寸长(很多)时,就会出现弹道传输。电子通过的介质的尺寸。
- 弹道传输通常在准一维结构中观察到。如碳纳米管或硅纳米线,因为在这些结构中存在极端的尺寸量化效应。这些材料中的极端尺寸量化效应。
- 弹道传输与超导性不同。
第五章 PN结的静电特性
PN结的相关概念
- PN结:A P-N junction is formed when an n type material is fused together with a p type material creating a semiconductor diode.
- P type: negative ions + majority holes + minority electrons
- N type: positive ions + minority holes + majority electrons
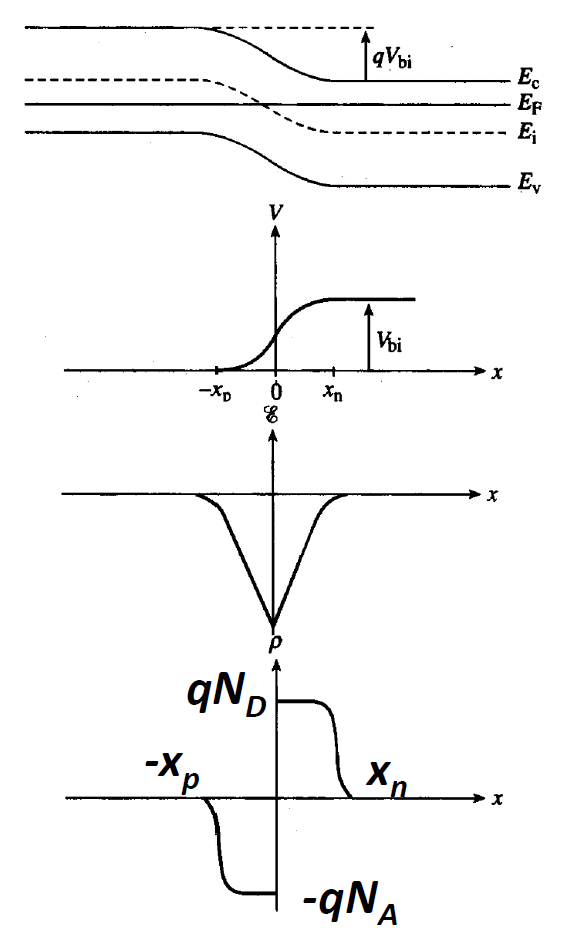
- 耗尽层/空间电荷区:电子和空穴在这里复合,载流子浓度几乎为0
- 准中性区:几乎和原来一样,呈现中性
- N型掺杂区和P型掺杂区的接触界面称为冶金结界面
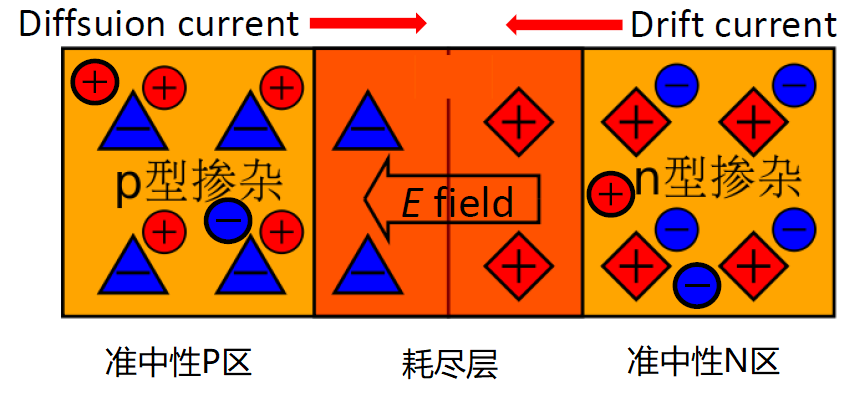
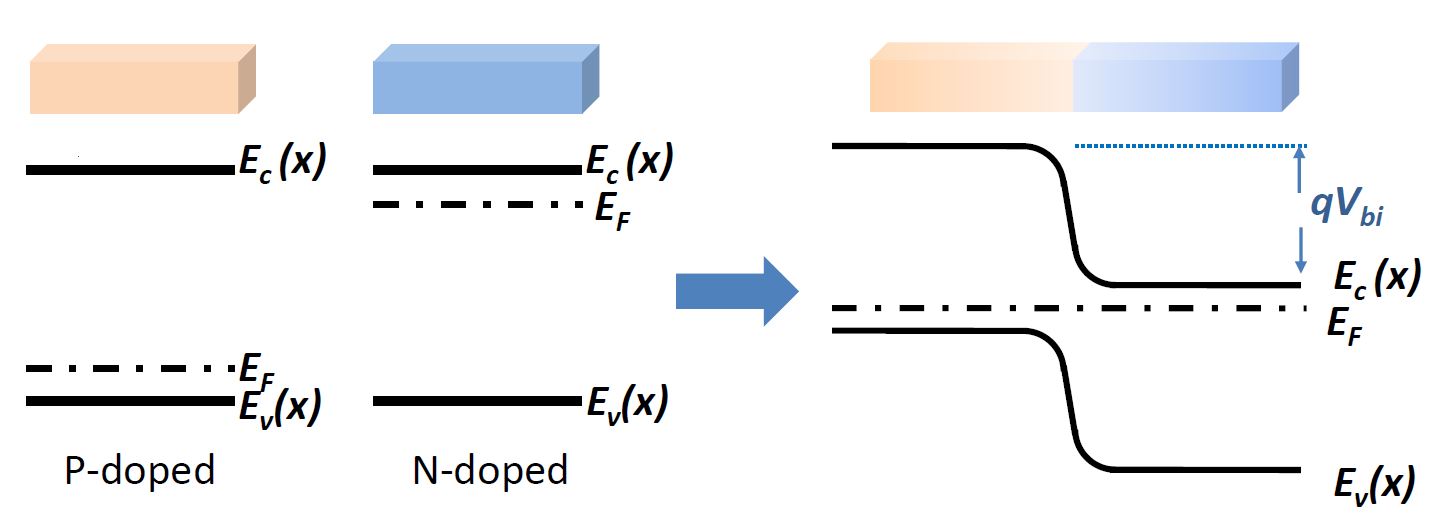
PN结的能带结构
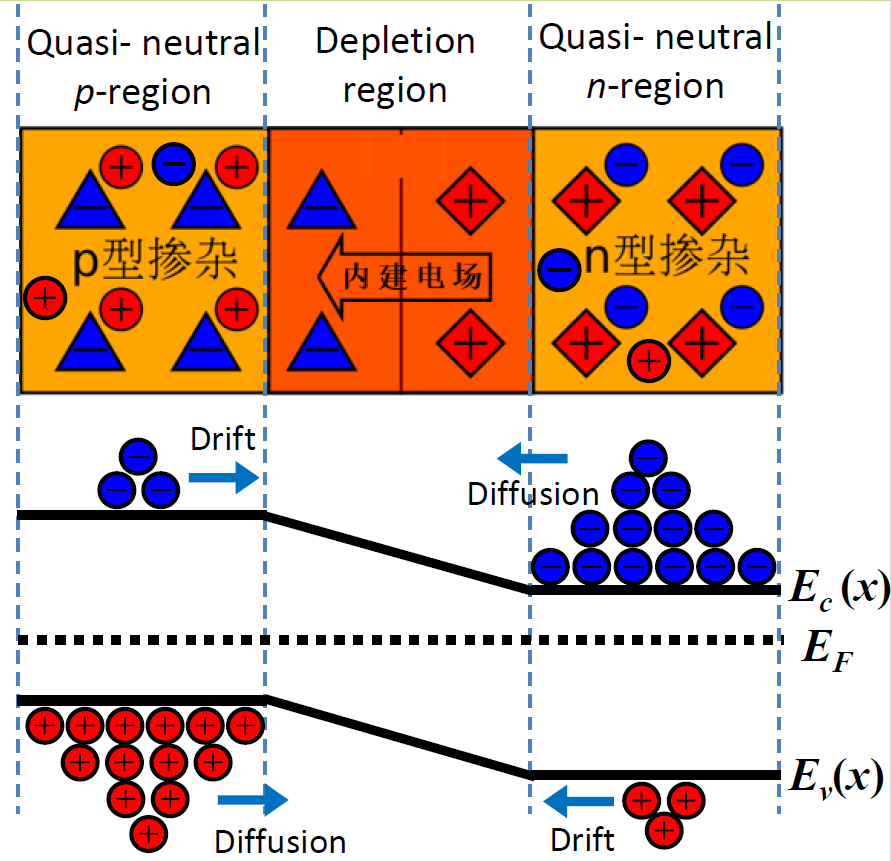
- 掺杂的电荷载流子沿载流子浓度梯度扩散
- 施主/受主离子保持固定,形成一个内建电场
- 在热平衡状态下,扩散电流与漂移电流相互补偿。
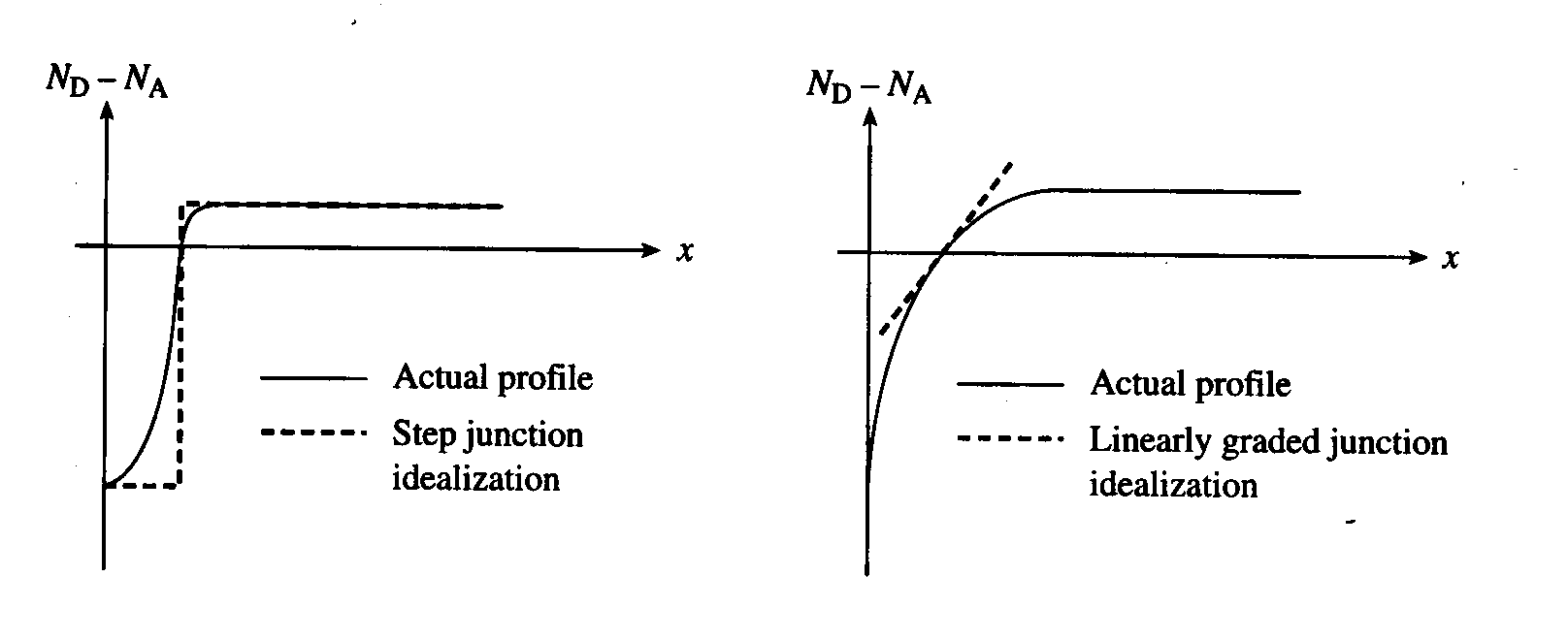
理想PN结
- 突变结:在交界面处,杂质浓度由 $N_A$ (p型)突变为 $N_D$ (n型)
- 线性缓变结:杂质浓度从p区到n区是线性变化的
电势、电场与电荷密度
内建电势差的计算
- 对于轻掺杂突变结:于是
- 对于 $p^{+}n$ 型突变结于是
- 对于 $n^{+}p$ 型突变结于是
- 对于线性缓变结于是
泊松方程
其中
- $\varepsilon_0=8.85\times 10^{-14}\mathrm{F}/\mathrm{cm}$ 是真空介电常数
- $K_s$ 是相对介电常数,对于硅,$K_s=11.9$
- $\rho$ 是载流子浓度
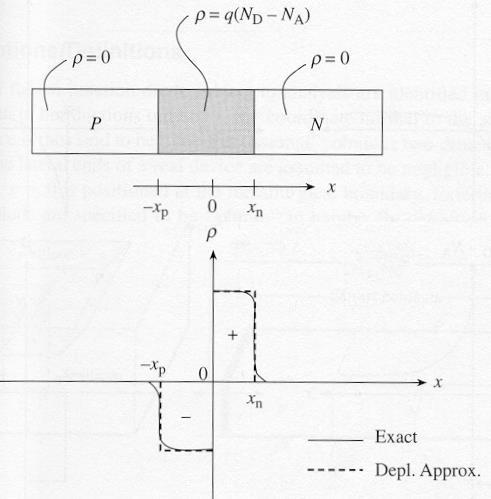
耗尽近似
- 准中性区电荷密度为0
- 耗尽层不存在自由载流子
突变结
- 耗尽层p区一侧电荷密度即为掺杂受主原子浓度 $N_A$,每个受主原子接收一个电子而变成带一个单位负电荷的阴离子
- 耗尽层n区一侧电荷密度即为掺杂施主原子浓度 $N_D$,每个施主原子发出一个电子而变成带一个单位正电荷的阳离子
电场强度分布
- 其中 $N_Ax_p=N_Dx_n$,电荷守恒
- 当 $x=0$ 即冶金结处,$E_m=-\frac{qN_Ax_p}{K_s\varepsilon_{0}}$
电势分布
- 其中
耗尽层宽度
联立
解得
单边突变结
在 $p^{+}n$ 型结中,$N_A\gg N_D$,$W\approx x_n$,$x_p\approx 0$,
线性缓变结
第六章 偏置电压下的PN结
偏置电压的影响
- 加入偏置电压后,电压几乎全部降落在耗尽层
电势、电场与电荷密度
对于突变结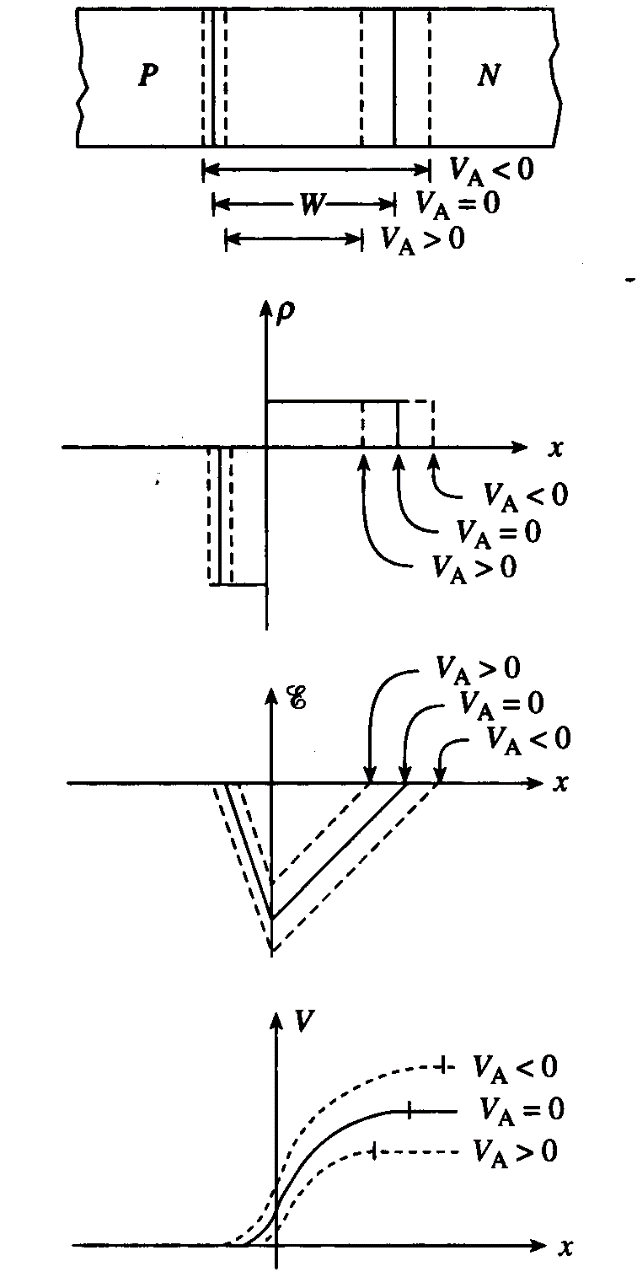
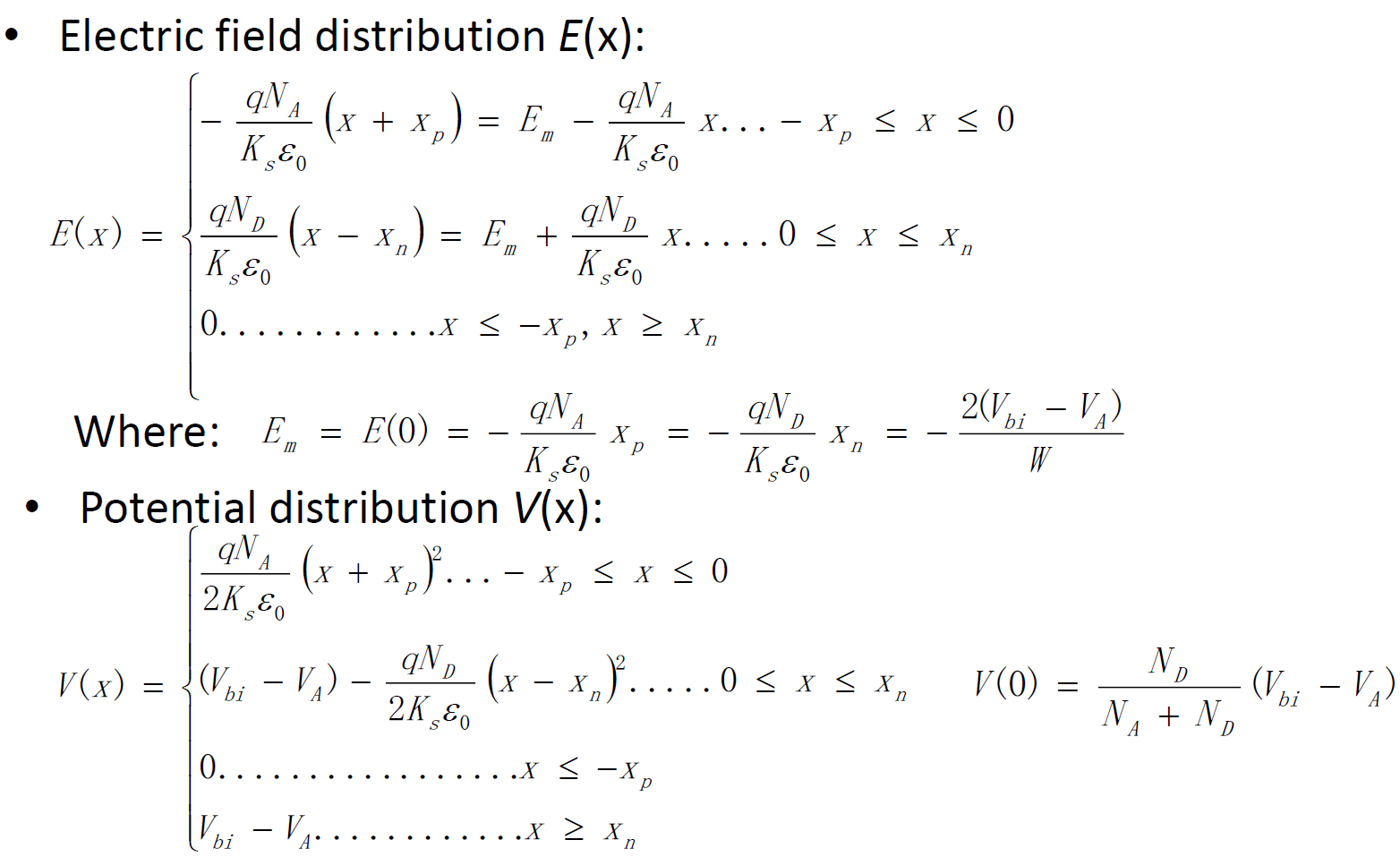
对于单边 $p^{+}n$ 型结
对于线性缓变结
能带图
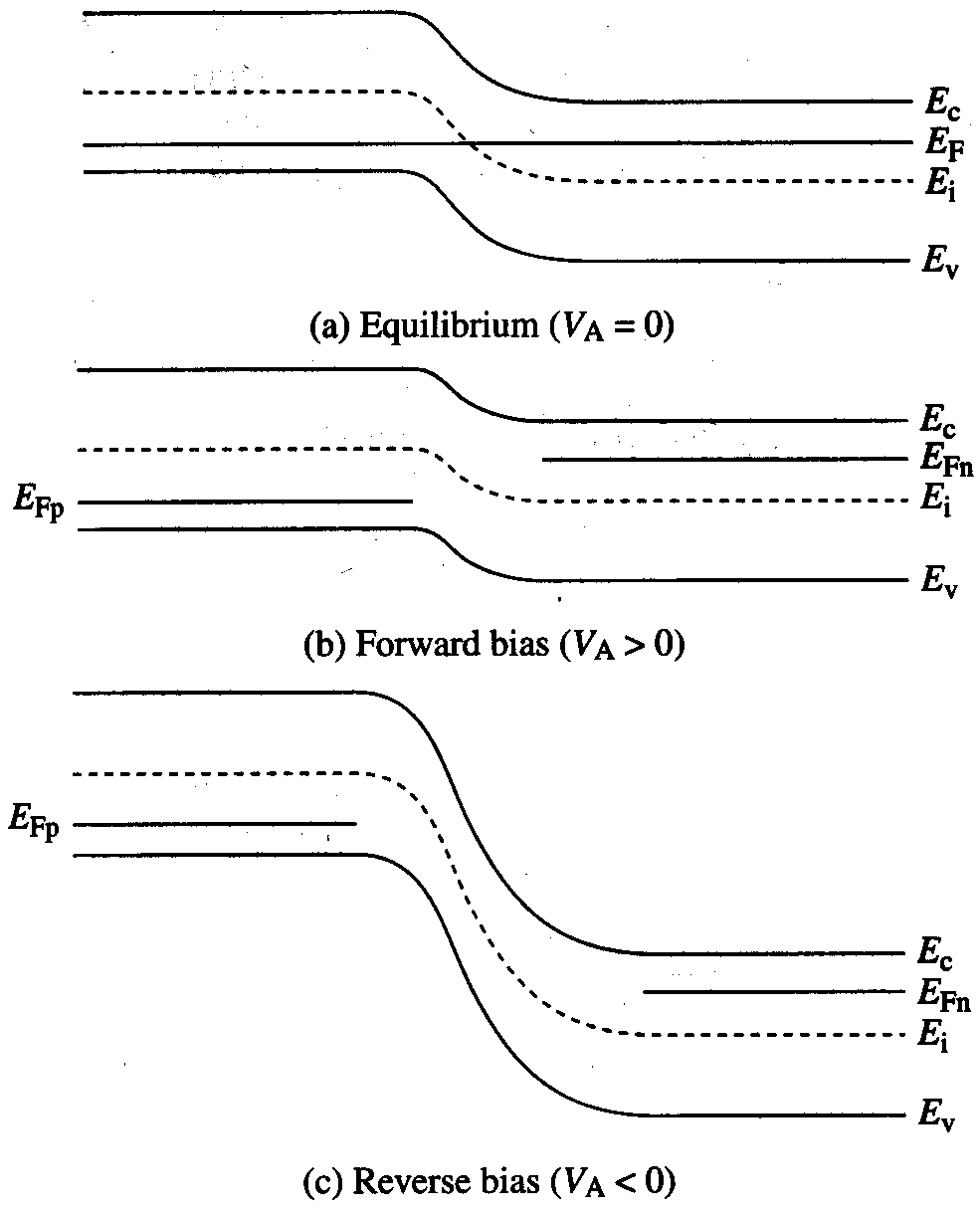
对漂移电流和扩散电流的影响
- 正偏电压作用下,耗尽层能带弯曲更小,多子扩散电流增强、少子漂移电流不变
- 反偏电压作用下,耗尽层能带弯曲更大,多子扩散电流减弱、少子漂移电流不变
电流与偏置电压的关系
(Todo)

PN结定律
可以合理地假设能级 $F_{\mathrm{N}}$ 和 $F_{\mathrm{P}}$ 会单调地变化,从远离结的 $p$ 型区域内的 $E_{\mathrm{Fp}}$ 过渡到远离结的 $n$ 型区域内的 $E_{\mathrm{Fn}}$。能级的单调变化会使二极管内各处有 $F_{\mathrm{N}}-F_{\mathrm{P}} \leqslant E_{\mathrm{Fn}}-E_{\mathrm{Fp}}=q V_{\mathrm{A}}$。如果假设在耗尽层内上面的 $F_{\mathrm{N}}-F_{\mathrm{p}}$ 表达式中等号成立,可以推断出
上式称为 pn 结定律。

理想二极管分析
前置条件
- 二极管是长基区二极管(准中性区长度远大于少子扩散长度)
- 二极管是一维的
- 非简并掺杂突变结
- 稳态
- 准中性区满足小注入条件
- 忽略耗尽层中电子空穴对的产生和复合
- 二极管内除了漂移、扩散和热复合-产生过程之外,没有其他过程。
计算过程
在准中性 P 区写出少子扩散方程,在准中性 N 区写出少子扩散方程
由“稳态”、“无其他过程”可得
由“小注入条件”可得准中性 P 区的多子空穴浓度与准中性 N 区的多子电子浓度
在 $-x_p$ 与 $x_n$ 处运用 PN 结定律,可得
由“长基区”条件可知
建立新坐标系,解得注入载流子浓度
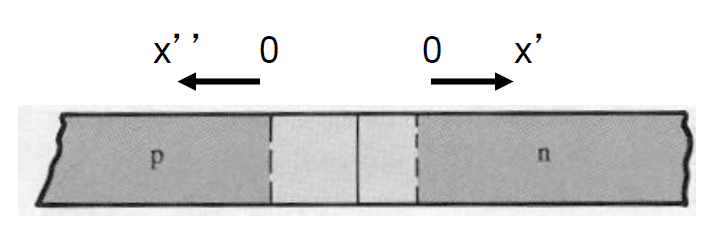
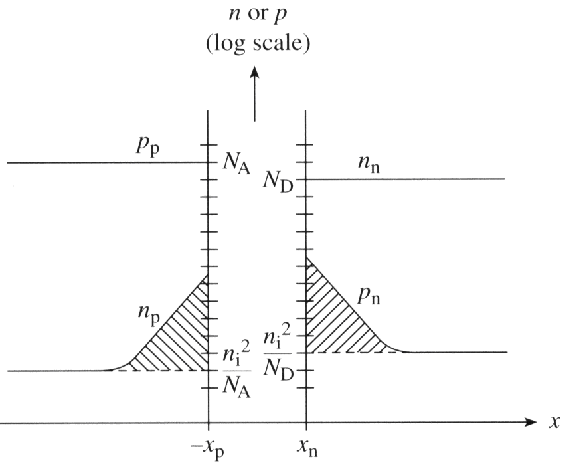
在耗尽层写出载流子连续性方程
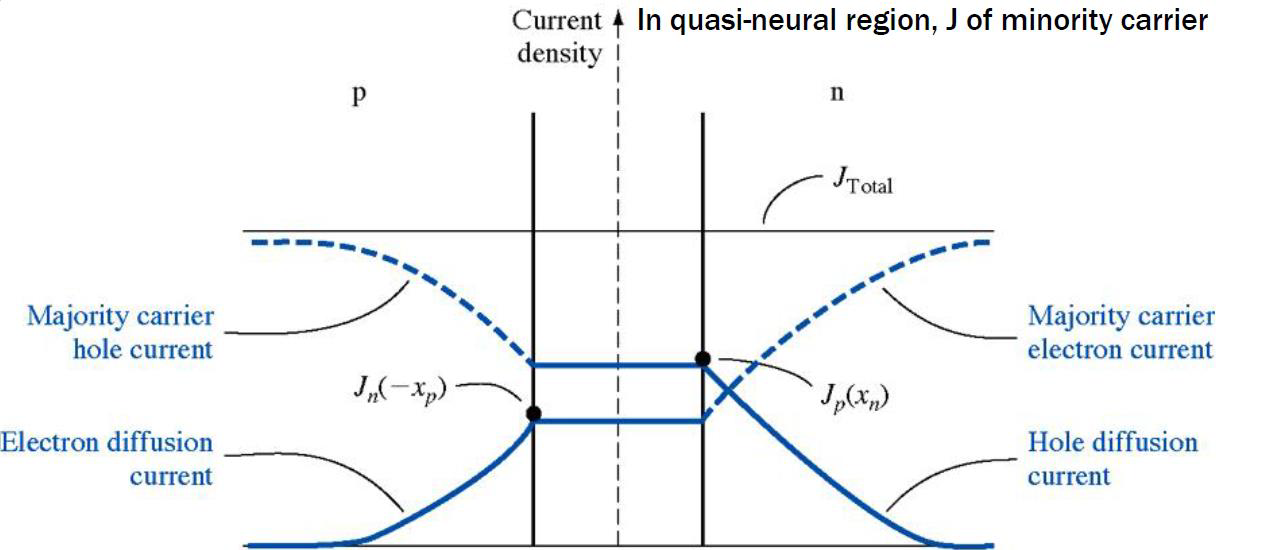
由于“稳态”“无 R-G 中心过程”“无光照”可知 $J_n$ 与 $J_p$ 不变
在准中性区写出总电流
由于“准中性区无电压降落”,电场为 0,可得
将 6 的结果代入可得
由于 $J_n$ 与 $J_p$ 不变,相加得总的电流密度
或者
其中
理想二极管方程(肖克利方程)
其中
- 在应用上,$I_0$ 取决于二极管本身的各种参数
- 在非对称掺杂(单侧)P-N 结中,与较重掺杂侧相关的项可以忽略不计
- p侧重掺杂:$I_{0} \cong A q n_{i}^{2}\left(\frac{D_{p}}{L_{p} N_{D}}\right)$
- n侧重掺杂:$I_{0} \cong A q n_{i}^{2}\left(\frac{D_{n}}{L_{n} N_{A}}\right)$
正反偏对载流子浓度、电流密度的影响
(Todo)
非理想电压电流关系
实际I-V曲线

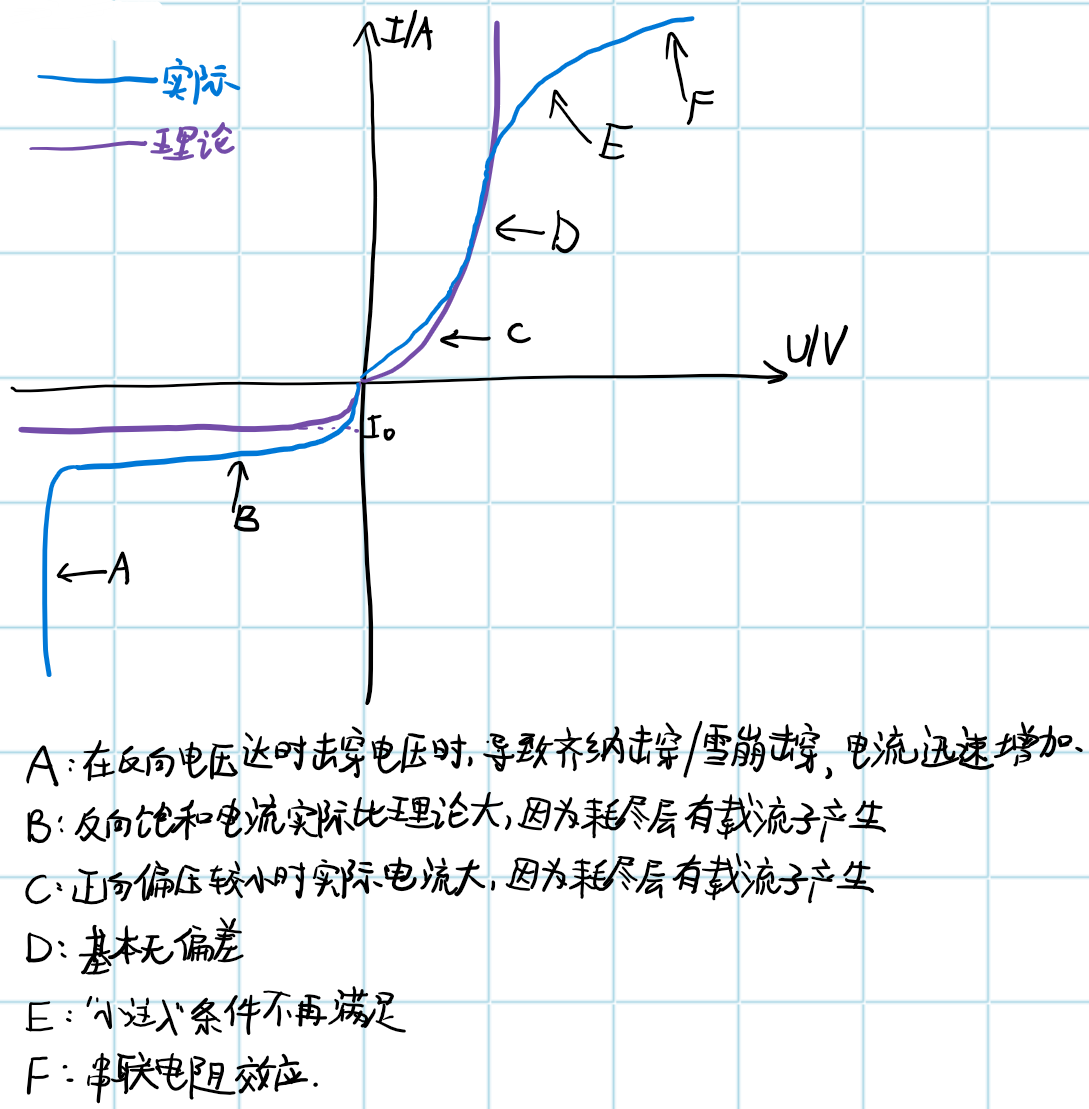
击穿电压
其中 $E_{C R}$ 是最大电场
击穿电压随掺杂浓度增加而减小,随带隙 $E_{G}$ 增加而增加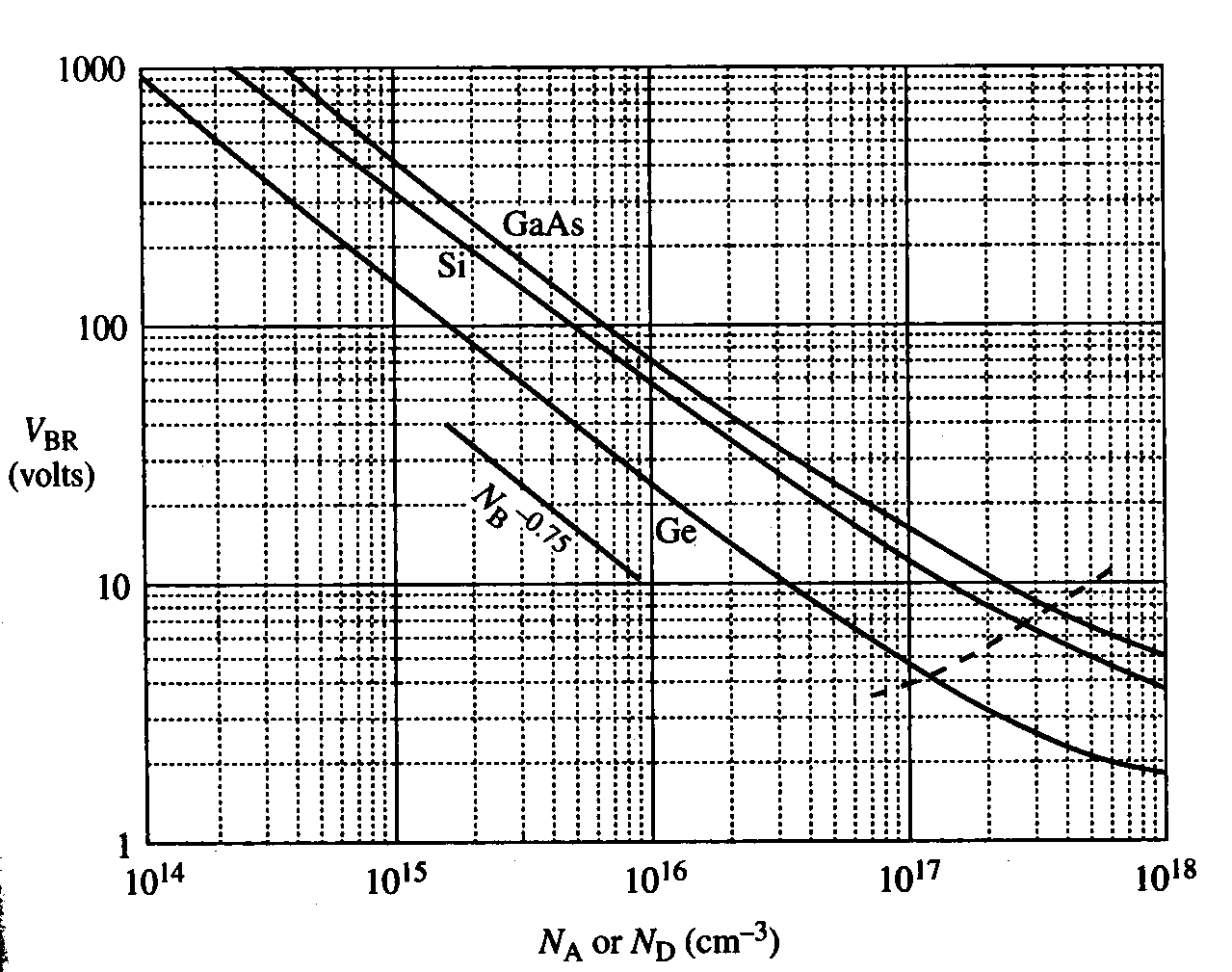
雪崩击穿
雪崩击穿是指在电场作用下,载流子能量增大,不断与晶体原子相碰,使共价键中的电子激发形成自由电子-空穴对。这种连锁反应使得阻挡层中的载流子的数量雪崩式地增加,流过PN结的电流就急剧增大击穿PN结,这种碰撞电离导致击穿称为雪崩击穿,也称为电子雪崩现象。
- $V_{BR}$ 随温度升高而增大,因为散射加剧,平均自由程减小了,需要更大的能量使雪崩发生
齐纳(量子隧穿)击穿
齐纳击穿是指在两侧高掺杂的pn结中,由于结很薄,即使外加电压并不高,就可产生很强的电场将结内共价键中的价电子拉出来,产生大量的电子-空穴对,使反向电流剧增。这种现象叫齐纳击穿。
- 通常结宽度小于 10nm,$V_{BR}<5V$
- $V_{BR}$ 随温度升高而减小,因为可用于隧穿的价带电子通量增加了
串联电阻效应
在准中性区域内存在着一个内在的电阻,由该区域的杂质浓度和尺寸来决定。在一个做好的器件中还存在着一个与二极管接触电极相关的微小残余电阻。这些加在一起组成了串联电阻 $R_{\mathrm{S}}$。在小电流情况下,串联电阻上的压降 $I R_{\mathrm{S}}$,与耗尽层上的压降相比可以完全忽略不计,耗尽层上的压降就是熟知的“结”电压 $V_{\mathrm{J}}$在上述情况中,$V_{\mathrm{J}}=V_{\mathrm{A}}$,正如静电学和理想二极管推导中的一样。然而,当电流足够大以至于 $I R_{\mathrm{S}}$ 与 $V_{\mathrm{A}}$ 可比时,耗尽层上的压降将减少为
实际上等于消耗掉了部分外加电压,为达到与理想二极管相同的电流,实际器件需要更大的外加电压,因此其特性斜率会变缓
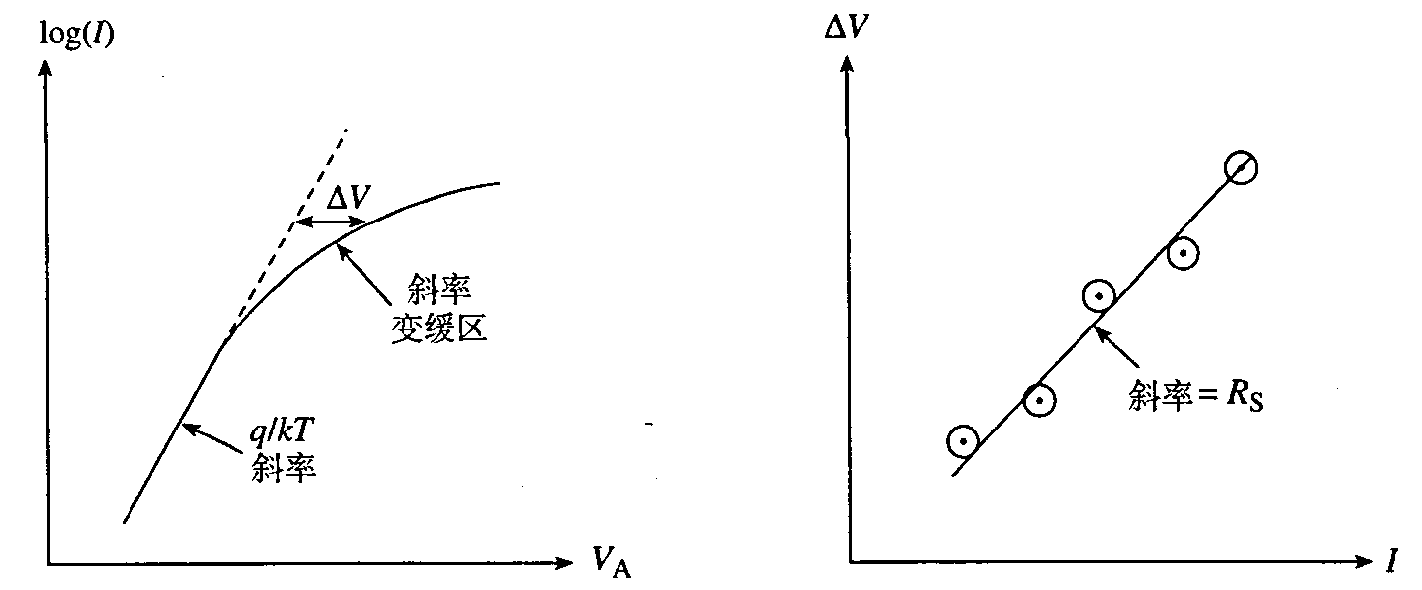
画出正向偏置下伏安关系的半对数坐标图,将图中理想二极管相关范围内的直线外延到斜率变缓区域,并记下两个曲线之间的电压差与 $I$ 的对应关系。因为 $\Delta V=V_{\mathrm{A}}-V_{\mathrm{J}}=I R_{\mathrm{S}}$,可以利用 $\Delta V$ 与 $I$ 交化关系图中的直线斜率得到 $R_{\mathrm{S}}$。
大注入
在轻掺杂一侧的耗尽层边界处,当结的少数载流子的浓度接近于杂质浓度时,理想二极管公式的推导过程采用的小电流注入假设开始失效。在室温下的 Si 中,当外加电压低于 $V_{\mathrm{bi}}$ 零点几个伏特时通常会出现这种情况。随着外加电压进一步地增加,则会导致大电流注入。在大电流注入条件下,邻近耗尽层处的少数载流子和多数载流子浓度都会出现波动。多数载流子浓度必须增加以维持准中性区域保持近似中性。对大电流注入的分析会得出电流大致正比于 $\exp (q / 2 k T)$。也就是说,在正向偏置 $I-V$ 特性的半对数坐标图中,预计大电流注入出现在 $q / 2 k T$ 区域内。但是,很难观察到预测的大电流注入对应的 $q / 2 k T$ 区域,因为与串联电阻相关的斜率下降效应会掩盖这种关系。尽管如此,也应该注意到大电流注入引起了载流子浓度的增大,这会导致观测到的串联电阻值出现下降。将大电流注入导致的电阻率下降现象称为电导调制。
复合-产生电流
- 室温下 Si 二极管中,正向小偏压和全部反向偏压下的电流都远大于理想二极管理论的预测值。观察到的“额外”电流都来自于耗尽层中载流子的热复合-产生过程,而理想二极管公式的推导将该过程忽略掉了。
- 当二极管处于反向偏置时,耗尽层中载流子浓度将会下降并低于其热平衡条件下的值,这导致了耗尽层内电子和空穴的产生。
- 耗尽层内巨大的电场会很快将产生的载流子扫到准中性区域,因此增大了反向电流。
- 正向偏置增加了耗尽层内的载流子浓度且高于其热平衡值,这导致了该区域内载流子出现复合。
- 复合-产生电流其中
- 反偏时,如果反偏电压大于几个 $kT/q$,绝大部分耗尽区内的载流子浓度都会变得很小。当载流子浓度变得可忽略不计时,其中
- 对于正向偏压,载流子浓度不能忽略不计,这里只能指出在正向偏压(大于几个 $kT/q$)下,预测 $I_{\mathrm{R}-\mathrm{G}}$ 粗略地按照 $\exp \left(q V_{\mathrm{A}} / \eta k T\right)$ 而变化,其中 $1<\eta \leqslant 2$。估算出 $\eta$ 的典型值接近于 $2$,而且正向和反向偏压下统一的依赖关系可近似表达为
窄基区二极管
- 当结的轻掺杂一侧准中性区域宽度与扩散长度同数量级或者更小时,则称这个二极管为窄基区二极管。
- 分析一个 $p^{+}n$ 型突变结二极管,除了 $n$ 型准中性区域宽度可能相当于或小于一个少数载流子扩散长度之外,该二极管与理想二极管几乎完全相同。
- $x_{\mathrm{c}}$ 是冶金结到 $n$ 型一侧接触电极的距离,而 $x_{\mathrm{c}}^{\prime}=x_{\mathrm{c}}-x_{\mathrm{n}}$ 为 $n$ 型一侧的耗尽层边界到 $n$ 型一侧接触电极的距离。假设 $n$ 型一侧的接触为欧姆接触,可令 $x^{\prime}=x_{\mathrm{c}}^{\prime}$ 处的 $\Delta p_{\mathrm{n}}=0$。
- 通常,接触电极与耗尽层边界之间的距离是有限的,该接触电极处的少数载流子浓度的大小依赖于接触电极处的载流子复合-产生率。在一个合格的或者是一个欧姆接触电极上,复合-产生率是很高的且少数载流子浓度保持在其热平衡值附近。
- 引入边界条件解得
- 若用双曲正弦函数表示,其中
- 最终结果
极限情况
- 本质上,可以将窄基区二极管的分析看作为理想二极管公式的通用表达形式,并且对任意厚度的准中性区域都适用。
- 当 $x_{\mathrm{c}}^{\prime} \rightarrow +\infty$,则退化为理想二极管的情况。
- 当 $x_{\mathrm{c}}^{\prime} \rightarrow 0$,可以将 $\Delta p_{\mathrm{n}}(x)$ 化简为非平衡载流子浓度成为位置的线性函数,就像用一条直线将边界条件设定的两个端点直接连接起来一样。在宽度小于一个扩散长度的区域内,忽略热复合-产生效应是合理的,这就直接导致了这个线性依赖关系。实际上,当准中性区宽度和扩散长度相比很小时,少数载流子扩散方程中的热复合-产生项可以忽略不计。
- 当 $x_{\mathrm{c}}^{\prime} \rightarrow 0$,即 $x_{\mathrm{c}}^{\prime} / L_{\mathrm{p}} \ll 1$ 的极限,$I_{0}^{\prime} \rightarrow q A\left(n_{\mathrm{i}}^{2} / N_{\mathrm{D}}\right)\left(D_{\mathrm{p}} / x_{\mathrm{c}}^{\prime}\right)$。随着反向偏压的升高,耗尽层宽度将随之增加,则准中性区域的宽度 $x_{\mathrm{c}}^{\prime}=x_{\mathrm{c}}-x_{\mathrm{n}}$ 将减小。因此得出 $I_{\mathrm{DIFF}}\left(V_{\mathrm{A}}<0\right) \cong-I_{0}^{\prime} \propto 1 / x_{\mathrm{c}}^{\prime}$ 不会出现饱和,但该电流会随着外加反向偏压而整体增大。
- 如果 $x_{\mathrm{c}}^{\prime}$ 充分地小,可能有 $x_{\mathrm{c}}^{\prime} \rightarrow 0$。在这种情况下,器件的整个区域都将耗尽,称其为穿通。
- 如果 $x_{\mathrm{c}}^{\prime} \rightarrow 0$,$I_{\mathrm{DIFF}}\left(V_{\mathrm{A}}<0\right) \rightarrow-\infty$。但是因为耗尽近似是用来确定准中性区域的宽度和特性的,因此在极端情况 $x_{\mathrm{c}}^{\prime} \rightarrow 0$ 下,理论公式将变得无效。在经验和更精确的理论公式中,当窄基区二极管处于穿通电压条件时,如果器件内的电场不足以产生雪崩击穿,则扩散电流依然保持为有限值。
电荷控制模型
- 电荷控制模型方法是利用基区中积累的少数载流子电量计算BJT电流的方法,与上面的理想二极管分析方法并列。
首先计算少子数量:
合理地假设 $\Delta p_{n}(x)$ 在少子扩散长度内为一定值,大于少子扩散长度为 $0$,即简化为阶梯状,则积分可以近似为
把少子扩散方程和电流密度方程联立
最后得到
本质上这就是载流子连续性方程。稳态下等号左边是 $0$,可得
注意这里使用了
这是前面运用 PN 结定律得到的结论。
对于窄基区,把少子寿命 $\tau_{p}$ 替换为少子迁移时间 $\tau_{tr}$,或者在结论里把 $L_N$ 替换成 $W_P^{\prime}$,把 $L_P$ 替换成 $W_N^{\prime}$
第七章 小信号导纳与瞬态响应
阻抗
阻抗是电路中电阻、电感、电容对交流电的阻碍作用的统称。阻抗是一个复数,实部称为电阻,虚部称为电抗。阻抗的大小是电压振幅与电流振幅的绝对值比率,阻抗的相位是电压与电流的相位差。阻抗的单位是欧姆,与电阻的单位相同。
三大元器件
- 电阻的阻抗 $Z_R=R$
- 电容的阻抗 $Z_C=1/j\omega C$
电感的阻抗 $Z_L=j\omega L$
容抗 $X_C=\operatorname{Im}(Z_C)=-1/\omega C$
- 感抗 $X_L=\operatorname{Im}(Z_L)=\omega L$
导纳
反偏结电容
- 反偏时,载流子浓度在耗尽层两侧交替变化,耗尽层相当于一个电容,
- 准静态假设:为了满足摆动的要求,多数载流子必须快速地流入和流出这个受影响的区域,而且需要和交流信号保持间步。换句话说,假定载流子能够对交流信号做出及时的响应,就如该信号是直流偏压的情况。在这种情况下,称该器件随交流信号而准静态地变化。在直流响应的讨论中,注意到在准中性区内的多数载流子能够快速地重新排列,而且多数载流子在接触电极处得到补充或排除。Si中多数载流子的典型响应时间 $~10^{-10}$ 秒或更小,那么在通常的情况下这里提出的准静态假设可以适用到非常高的信号频率上。
- 一般化地,假设一边重掺杂 $(x<0)$ 而轻掺杂一边的杂质浓度服从指数关系:其中在给定的分布下 $b>0$ 且 $m$ 为常数。注意 $m=0$ 和 $m=1$ 分别对应于非对称突变结和单边线性缓变结。而且注意到允许出现负的 $m$ 值。$m<0$ 的分布,即离结越远杂质浓度越低,称为超突变分布,可以通过离子注入和外延形成超突变结。
- 在一个单边指数分布的 $pn$ 结二极管中,$m>-2$ 时的耗尽层宽度关系式为
- 代入电容公式可得若引入 $V_A=0$ 时的电容则电容还可以写成
变容二极管
上式描述的电容-电压变化关系的 pn 结二极管称为变容二极管。变容二极管广泛应用于参数放大、谐波发生、混频、检波和电压可变调制中。在这些应用中,通常期望在给定的电压范围内二极管表现出最大的电容比,这个优值指标称为调制率(TR)。反偏下 $-V_{\mathrm{A}} / V_{\mathrm{bi}}\gg 1$, 得到
最大调制率对应于 $m$ 值最小的器件——线性缓变 $(m=1)$ 到突变 $(m=0)$,再到超突变 $(m<0)$ 结,TR 逐渐增大。
单边突变结参数测量
对于单边突变结,$m=0$,$b=N_B$,于是有
作出 $1/C_{\mathrm{J}}^{2} - V_A$ 图,则斜率的倒数正比于轻掺杂一侧浓度 $N_B$,横轴截距为 $V_{\mathrm{bi}}$。又根据
可以求出重掺杂一侧浓度。
反偏偏置电导
反向偏置条件下,少数载流子数目太少,其对导纳的贡献可忽略不计。引入符号 $G_0$ 表示低频交流电导,交流电导等于微分直流电导,即
代入理想二极管方程得
- 当反向偏压大于几个 $\frac{kT}{q}$ 时,$I\rightarrow I_0$,则 $G_0\rightarrow 0$
- 当反向偏压等于几个 $\frac{kT}{q}$ 时,$I_{R-G}$ 占主导,
正偏导纳
- 正向偏置下,对于多数载流子来说没有出现什么新的机制,这些载流子仍然在耗尽层边界处移进和移出,从而引起结电容。上面推导出的 $C_{\mathrm{J}}$ 关系式可以不做任何修改,直接应用到正向偏置的情况。
- 二极管正向偏置会在邻近耗尽层的准中性区内引起少数载流子的堆积。随着正向偏压的增加,该载流子的堆积会变得越来越明显。为了响应一个交流信号,过剩少数载流子需要在其直流值附近的分布涨落。
- 如果少数载流子能够跟随信号准静态地变化,那么图中的载流子可以在两条直线之间上下变化。但是,少数载流子的补充和抽取并不像多数载流子变化得那样快,在角频率接近少数载流子寿命的倒数时,少数载流子电荷的涨落将很难与交流信号保持同步,结果是空间电荷表现为异步地变化,这个电荷异步涨落会增加测量电导而减小测量电容。
- 因为少数载流子在耗尽层边界的积累是由扩散电流引起的,所以将少数载流子电荷的涨落导致的导纳称为扩散导纳 $Y_D$。通常给出其中 $C_D$ 和 $G_D$ 分别是扩散电容和扩散电导。
求解
将少子浓度变化分成直流分量和交流分量
在准中性 P 区和 N 区写出少子扩散方程
边界条件
解得直流分量(就是第六章得到的结果)
解得交流分量
其中
可得交流小信号导纳
电导和电纳分量
在低频下
瞬态关断
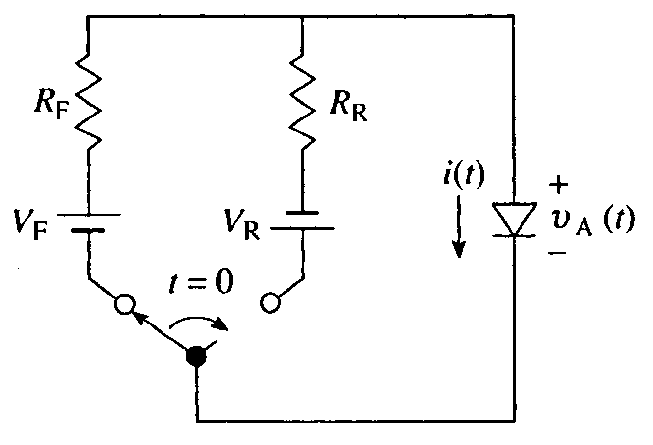
对于理想的开关电路,$t=0$ 之前在二极管两端加上正向偏置电压,有稳态正向电流 $I_F$ 流过二极管;在 $t=0$ 时刻电路中的开关快速移到右边。对于开关应用,希望二极管电流从 $I_{\mathrm{F}}$ 立刻下降到与所加反偏电压对应的小的稳态反偏电流上。而实际上观测到的结果如下图所示
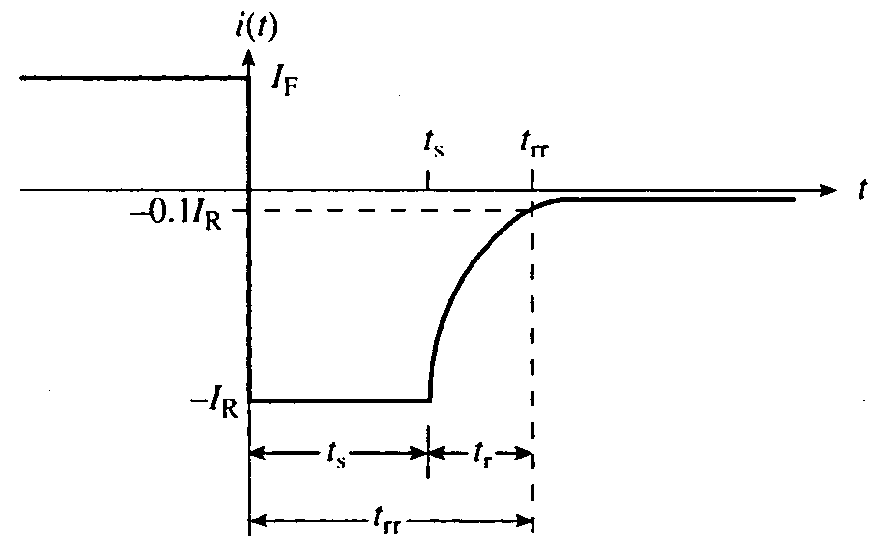
如果 $V_{\mathrm{R}} / R_{\mathrm{R}} \sim V_{\mathrm{F}} / R_{\mathrm{F}}$,在开关转换后的瞬间,反向电流的大小就与正向电流相当,而不是一个逐渐减少的电流。随后,在电流最终衰减到稳态值之前的有限时间内,流经二极管的电流基本上保持常数,大小为 $-I_R$ 。反向电流保持为常数的这段时间称为存贮时间或存贮延迟时间($t_\mathrm{s}$)。当反向电流衰减到它最大数值的10%时所需的总时间定义为反向恢复时间($t_{\mathrm{rr}}$),而恢复时间($t_{\mathrm{r}}$)是 $t_{\mathrm{rr}}$ 和 $t_{\mathrm{s}}$ 之差。

上图显示了与 $i-t$ 瞬态相对应的二极管瞬时电压 $\left(v_{\mathrm{A}}\right)$ 的变化。从图中可以看出
- 在 $0<t<t_{\mathrm{s}}$ 区间结保持正偏,即使外加电压达到使二极管反偏的程度也仍然如此。
- 在 $t=t_{\mathrm{s}}$ 点处 $v_{\mathrm{A}}=0$。
可采用两种方法把准中性区内过剩少数载流子的电荷移走
- 第一种方法是通过复合在原来位置消除载流子。显然,复合过程不可能立刻就完成,如果复合是移走载流子的惟一方式,那么从开态转换到关态所持续的时间与少数载流子寿命相同。
- 第二种消除过剩载流子的方法是通过净载流子漂移完成。一旦撤除外部的维持偏压,这些少数载流子会流回结的另一边,也就是它们变成多数载流子的地方。可以想像,这种反向注入能以非常快的速度发生。然而,每秒钟能移走的少数载流子数量受到外部开关电路的限制。如果把二极管短路,可以实现非常快的瞬态过程,但这一方法很可能导致电流超出器件的容限从而损坏二极管。
- 总之,有复合和反向电流两种机理来完成对过剩存贮电荷的消除,在不损坏器件的前提下,两种机理中没有一种能以足够快的速度把电荷完全消除,因此在从开态到关态的转换中会观察到延迟时间。
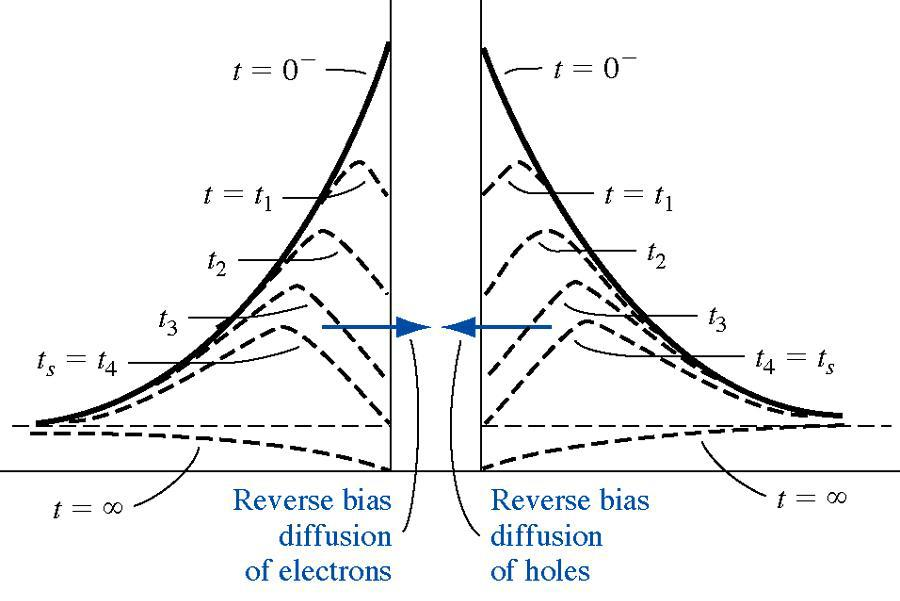
在耗尽区边界的少数载流子浓度超过平衡值时,就意味着结处于正向偏置状态。换个角度来讲,正是由于耗尽区边界和耗尽区内部过剩载流子的存在才使整个结保持正偏。只有当 $x=x_n$ 处的空穴浓度下降到平衡值以下时,二极管才会变成反偏。
存贮延迟时间计算
由电荷控制模型知
边界条件无法准确确定,我们假设当 $t=t_s$ 时 $Q_p=0$,得到
瞬态开启
当二极管电流从占主导地位的反偏值瞬间改变到一个常数值即正偏电流 $I_F$ 时,二极管两端的电压降 $v_{\mathrm{A}}(t)$ 从 $t=0$ 时的 $V_{\mathrm{OFF}}$ 单调上升到 $t=\infty$ 时的 $V_{\mathrm{ON}}$ 在响应的第一阶段,即从 $t=0$ 到 $v_{\mathrm{A}}=0$ 的过程极其短暂,用来把结电压提高到 $0 \mathrm{~V}$ 的少数几个少子迅速注人到耗尽区,多数载流子也迅速再分布以使耗尽区缩小到 0 偏压下的宽度。瞬态过程的第一部分非常短暂,以至于好像二极管是在 $t=0$ 时从 $i=0$ 触发到 $i=I_{\mathrm{F}}$ 的。
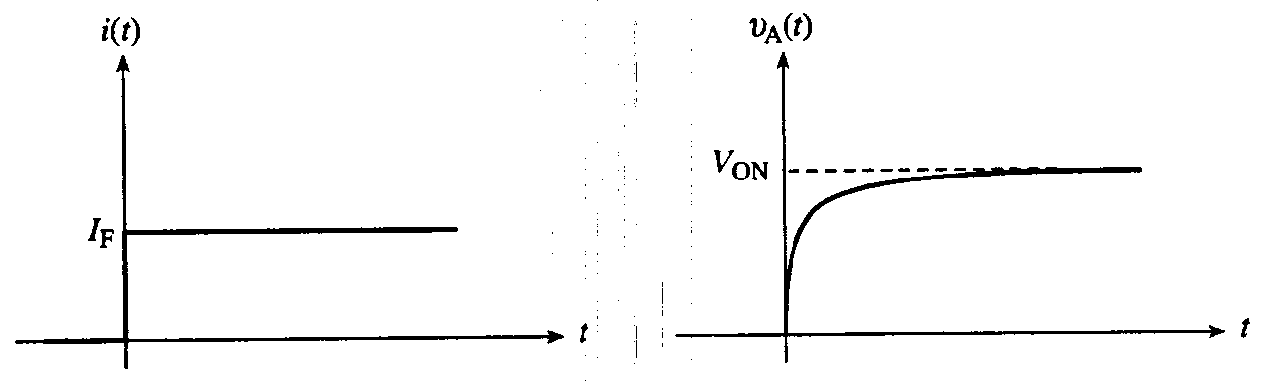
压降的计算
由电荷控制模型
解得
在稳态时的条件
假设稳态条件对于非稳态也成立
联立得
第八章 金属半导体接触
MS接触特性
- 理想的 MS 接触具有以下特点:
- 假定金属和半导体在原子尺度上紧密地接触,在两者之间不存在任何类型的夹层(例如氧化物)
- 金属和半导体之间不存在互扩散或混合
- 在 MS 界面没有吸附的杂质或表面电荷。
- 理想 MS 接触的能带图中,平带(零电场)条件存在于整个半导体中。此外,位于两个图中能带终止处的垂直线表示表面,图中斜线阴影部分表示几乎全部为电子填满的所允许的电子态。
金属和半导体能带相关的物理量
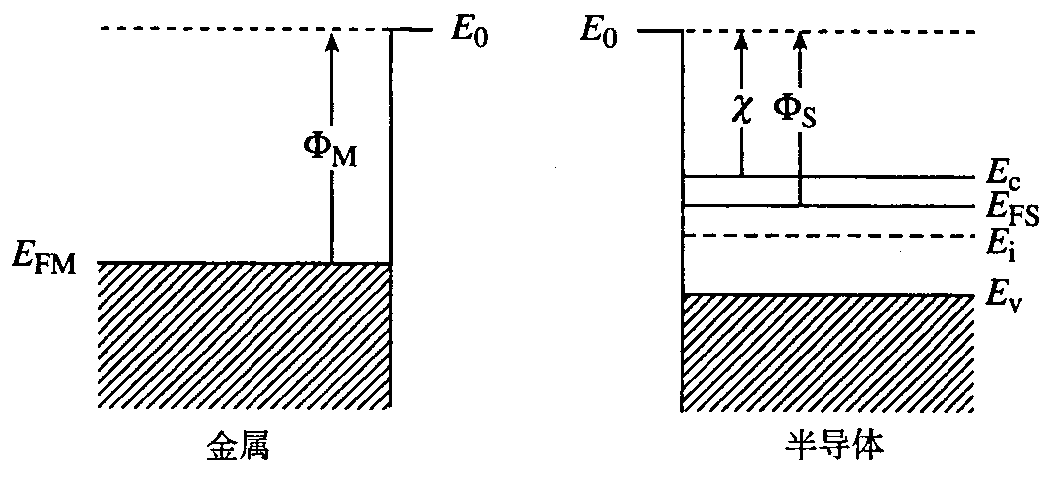
- 垂直直线的顶部代表电子完全脱离材料本身所必须具有的最小能量,它称做真空能级 $E_{0}$,真空能级和费米能级之间的能量差称为材料的功函数($\Phi$)
- 金属功函数 $\Phi_{\mathrm{M}}$ 对于一定的金属来说是一个不变的基本参数。$\Phi_{\mathrm{M}}$ 的数值范围可以从 $3.66 \mathrm{eV}$(镁)到 $5.15 \mathrm{eV}$(镍)。
- 半导体功函数 $\Phi_{\mathrm{s}}$ 则由两个不同的部分组成,它们是
- 电子亲和势 $\chi \equiv\left.\left(E_{0}-E_{\mathrm{c}}\right) \right|_{\mathrm{surface}}$,对于一定的半导体材料来说 $\chi$ 是一个恒定的基本参数。$\left(E_{\mathrm{c}}-E_{\mathrm{F}}\right)_{\mathrm{FB}}$ 是在平带或零电场条件下 $E_{\mathrm{c}}$ 和 $E_{\mathrm{F}}$ 之间的能量差,它是半导体掺杂的函数,是可计算的。
MS接触
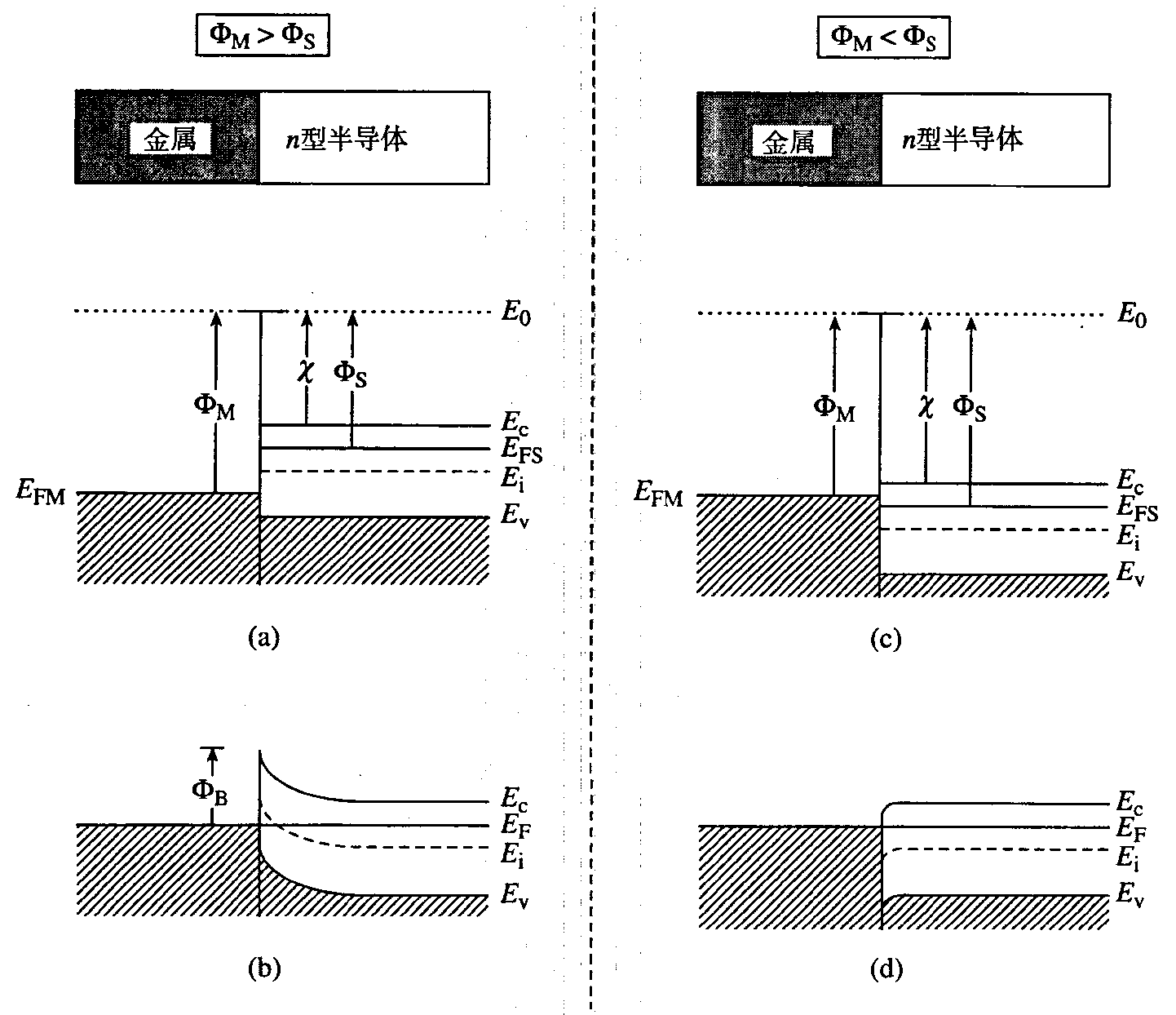
n型半导体,$\Phi_{\mathrm{M}}>\Phi_{\mathrm{S}}$
- 假设 $\Phi_{\mathrm{M}}>\Phi_{\mathrm{S}}$ 的金属和 $n$ 型半导体组合在一起,形成理想的 $\mathrm{MS}$ 接触。假定接触形成几乎是瞬时的,在接触过程中两种材料之间的电子转移可以忽略。图中各自独立的两个部分的能带图以公共的 $E_{0}$ 参考能级为基准而垂直地对齐,并简单地在界面处对接。应该强调的是,$\Phi_{\mathrm{M}}$ 和 $\chi$ 是材料的常数,在接触形成过程中保持不变。这样的接触是肖特基接触。
- 由于 $E_{\mathrm{FS}} \neq E_{\mathrm{FM}}$,MS 接触特性明显处于非平衡态。为了保证费米能级一致,不随位置变化而改变,电子开始从半导体向金属内转移。半导体中的电子净损失会导致表面耗尽区和电子势垒增加,阻止电子从半导体向金属的转移,一直持续到通过界面的转移速率在两个方向上都相同,而且 $E_{\mathrm{F}}$ 在整个结构中都一样。
- 最后,理想的 $\Phi_{\mathrm{M}}>\Phi_{\mathrm{S}}$ 的金属与 $n$ 型半导体接触的平衡态能带图如图 (b) 所示。
- 图中可以注意到 $\Phi_{\mathrm{Bn}}=\Phi_{\mathrm{M}}-\chi$ 被称为肖特基势垒
- 半导体一侧耗尽层势垒高度 $qV_{bi}=\Phi_{\mathrm{M}}-\Phi_{\mathrm{S}}=\Phi_{\mathrm{Bn}}-\left(E_{\mathrm{c}}-E_{\mathrm{F}}\right)_{\mathrm{FB}}$
n型半导体,$\Phi_{\mathrm{M}}<\Phi_{\mathrm{S}}$
- 这样的接触是欧姆接触
- 电子开始从金属向半导体内转移。半导体结区一侧电子浓度进一步增加
- 半导体一侧电子很容易到达金属一侧,金属一侧电子也很容易到达半导体一侧
p型半导体,$\Phi_{\mathrm{M}}<\Phi_{\mathrm{S}}$
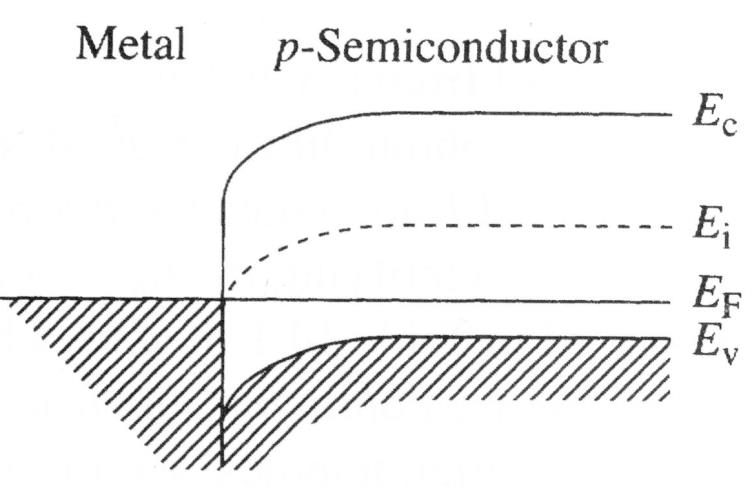
- 这样的接触是肖特基接触
- 电子开始从金属向半导体内转移。半导体结区一侧电子和空穴复合,加宽耗尽层
- 肖特基势垒 $\Phi_{\mathrm{Bp}}=\chi+E_G-\Phi_{\mathrm{M}}$
- 半导体一侧耗尽层势垒高度 $qV_{bi}=\Phi_{\mathrm{S}}-\Phi_{\mathrm{M}}=\Phi_{\mathrm{Bp}}-\left(E_{\mathrm{F}}-E_{\mathrm{v}}\right)_{\mathrm{FB}}$
p型半导体,$\Phi_{\mathrm{M}}>\Phi_{\mathrm{S}}$
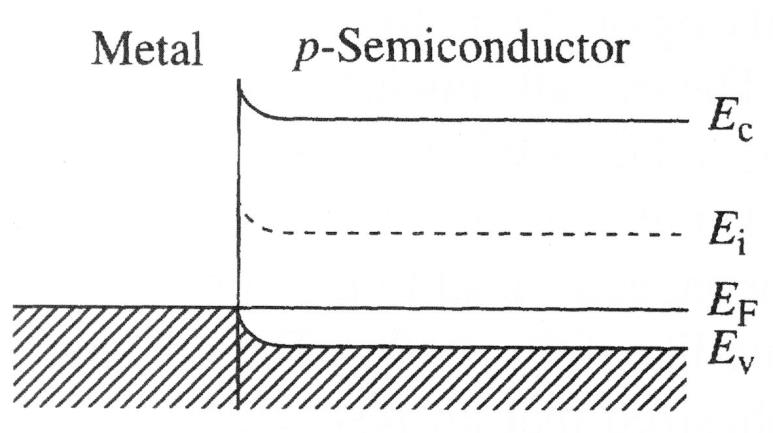
- 这样的接触是欧姆接触
- 电子开始从半导体向金属内转移。半导体结区一侧空穴浓度进一步增加
- 半导体一侧电子很容易到达金属一侧,金属一侧电子也很容易到达半导体一侧
耗尽近似
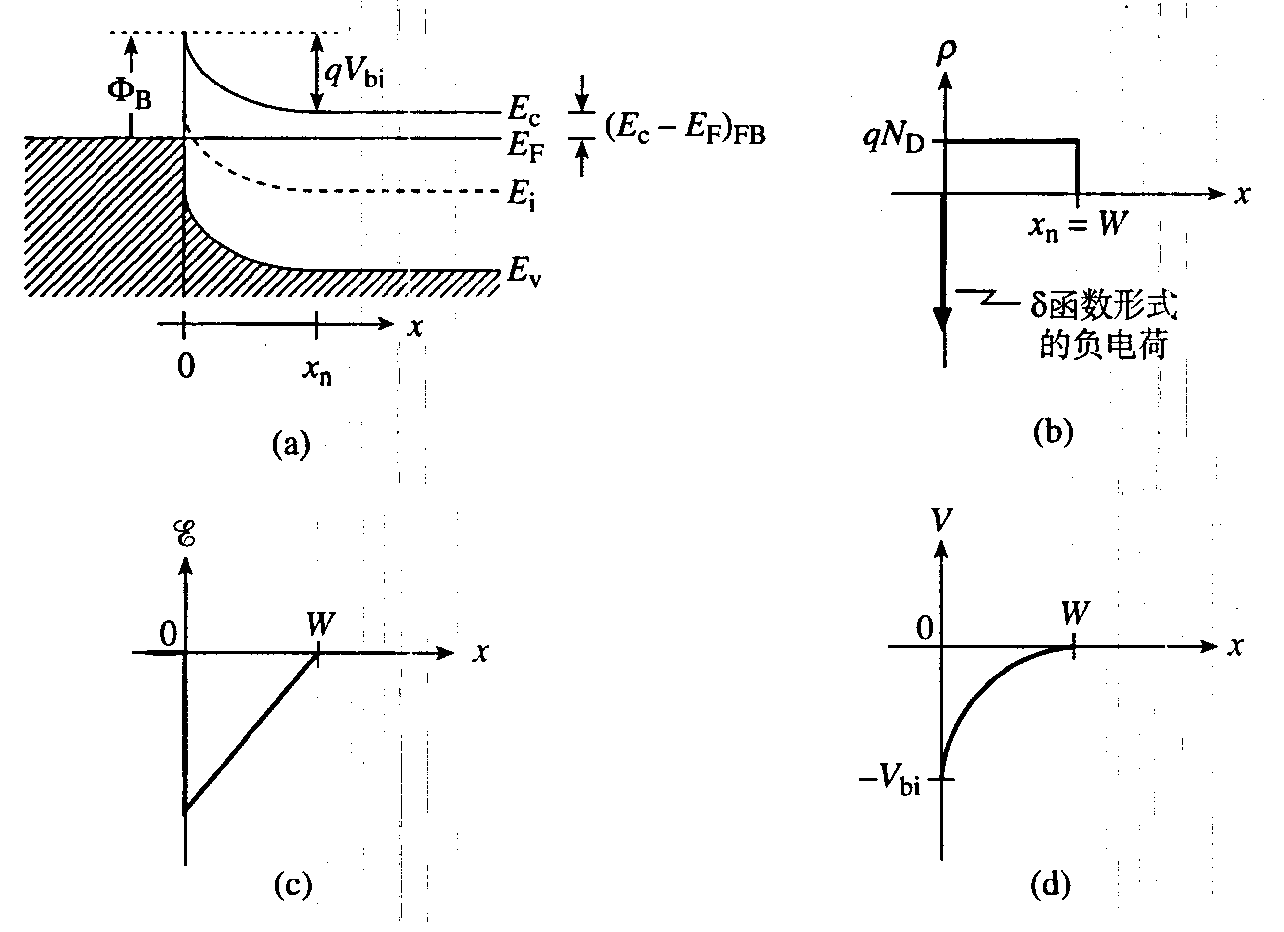
在紧邻 MS 界面的半导体中存在一个电子耗尽区。与 pn 结二极管类似,在 n 型半导体中耗尽区的宽度为 $x_{n}$,该耗尽区中具有施主离子产生的净正电荷。然而与 pn 结不同的是,没有 p 型一侧的负的受主电荷来平衡 n 型一侧的正的施主电荷。在 MS 接触中,负电荷(过剩电子)以类似 $\delta$ 冲激函数的形式在直接紧邻界面的金属中堆积。
在 MS 接触的半导体一侧,电场和电荷密度通过泊松方程联系起来
代入边界条件 $\mathscr{E}(W)=0$ 解得
积分可得电势分布
在 $x=0$ 处电势为 $V_A-V_{bi}$,代入得耗尽层宽度
对于p型半导体
I-V特性

- 在 MS(n型)二极管中,正偏时 $E_c$ 升高,对半导体中的电子来说势垒相对较低,电流主要来源于从半导体进入到金属中的电子注入。
- 在反偏条件下半导体一侧电子难以到达金属,电流主要来自于金属侧的电子获得热激发能量越过肖特基势垒。
- MS 二极管通常称为“多数载流子器件”
考虑一个电子从半导体体内进入到耗尽区,如果该电子具有指向界面方向的速度 $v_{x}$,并且 $v_{x}$ 满足
正偏总电流表达式
积分得
其中
反偏热激发电流始终不变且在 $V=0$ 时与正偏电流抵消
小信号电容
实际欧姆接触与比接触电阻率
- 由于费米能级钉扎效应的存在,实际的接触往往不能有低势垒
- 通过重掺杂,减小耗尽层宽度,使量子隧穿容易发生
- $\rho_C$ 定义为每 $1\mathrm{cm}^2$ 的接触电阻
- 对于理想欧姆接触,$\rho_C \propto e^{H\Psi_{B}/\sqrt{N_D}}$
- 理想情况下欧姆接触电阻很小,压降可以忽略不计
本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 协议 ,转载请注明出处!