半导体器件原理笔记
本文最后更新于:2023年10月7日 上午
置顶
符号含义对照表
| 名称/解释 | PPT 任鹏鹏 |
半导体物理与器件 Neamen |
半导体器件基础 Pierret |
现代VLSI器件基础 Yuan Taur |
|---|---|---|---|---|
| 金属表面积累的电荷 | $Q_m$ | |||
| 半导体内的空间电荷 | $Q_s$ | |||
| 氧化层厚度 | $t_{ox}$ | $t_{ox}$ | $x_o$ | $t_{ox}$ |
| 表面势 | $V_s$ | $\phi_{s}$ | $\phi_{S}$ | $\Psi_{s}$ |
| 栅电压 | $V_g$ | $V_{G}$ | $V_{G}$ | $V_g$ |
| 受主杂质浓度 | $N_A$ | $N_a$ | $N_A$ | $N_a$ |
| 金属-半导体功函数差 | $\phi_{ms}$ | $\phi_{ms}$ | ||
| 半导体内部本征费米能级 | $E_{i0}/E_{Fi}$ | |||
| 半导体内部本征费米能级与费米能级的势垒高度 | $V_{B}$ | $\phi_{fp}/\phi_{fn}$ | $\phi_{F}$ | $\Psi_{B}$ |
| 德拜长度(p型) | $L_D$ | $L_D$ | ||
| 半导体介电常数 | $\varepsilon_s$ | $\epsilon_s$ | $K_S$ | |
| 氧化层介电常数 | $K_O$ | |||
| 半导体表面面电荷密度 | $Q_s$ | $Q_s$ | ||
| 反型层面电荷密度 | $Q_i$ | |||
| 空间电荷宽度 | $d$ | $x_{d}$ | $W$ | $W_d$ |
| 最大空间电荷宽度 | $d_{max}$ | $x_{dT}$ | $W_T$ | $W_{dm}$ |
| 阈值电压 | $V_t$ | $V_T$ | $V_T$ | |
| 平带电压 | $V_{fb}$ | $V_{FB}$ | $V_{fb}$ | |
| 氧化层降落电压 | $V_{ox}$ | $V_{ox}$ | $V_O$ | $V_{ox}$ |
| 单位面积氧化层电容 | $C_{ox}$ | $C_{ox}$ | $C_{O}$ | $C_{ox}$ |
| 平带电容 | $C_{FB}$ | $C_{FB}$ | $C_{fb}$ | |
| 单位面积可移动电荷 | $Q_{m}$ | |||
| 单位面积氧化层陷阱电荷 | $Q_{ot}$ | |||
| 单位面积氧化层固定电荷 | $Q_{f}$ | |||
| 单位面积界面陷阱电荷 | $Q_{it}$ |
MOSCAP
理想MOS结构的定义
- MOS 电容是一个简单的两端器件,由硅衬底和金属极板之间夹一薄层 $\mathrm{SiO}_{2}$ 层($0.01 \mu \mathrm{m} \sim 1.0 \mu \mathrm{m}$)组成,最通用的极板材料是铝和重掺杂多晶硅,第二层金属层一般沿半导体背面,作为硅衬底的电接触。连到极板的电极和极板本身称为栅,硅端接地并简称为背接触或衬底接触。
- 理想 MOS 结构具有下列明显特点:
- 金属栅足够厚,在交流和直流偏置条件下可以看作为一个等电势区
- 氧化层是一个完美的绝缘体,在所有静态偏置条件下没有电流流过氧化层
- 在氧化层中或氧化层-半导体界面没有电荷中心
- 半导体均匀掺杂
- 半导体足够厚,不管加什么栅电压,在达到背接触之前总有一个零电场区域(即所谓硅体区)
- 半导体与器件背面金属之间处于欧姆接触
- MOS 电容是一维结构,假设所有变量仅是坐标 $x$ 的函数
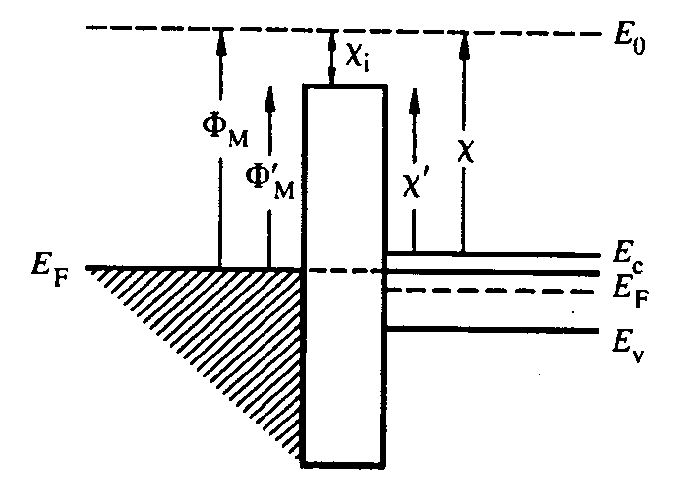
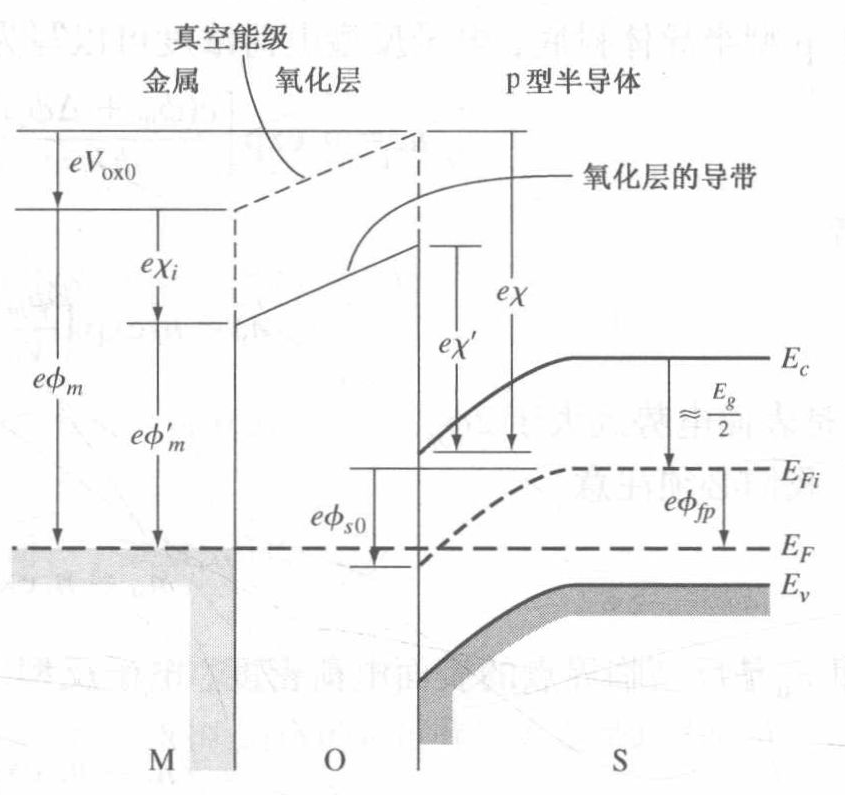
- $\Phi_{\mathrm{M}}=\Phi_{\mathrm{S}}=\chi+\left(E_{\mathrm{c}}-E_{\mathrm{F}}\right)_{\mathrm{FB}}$
理想MOS能带图
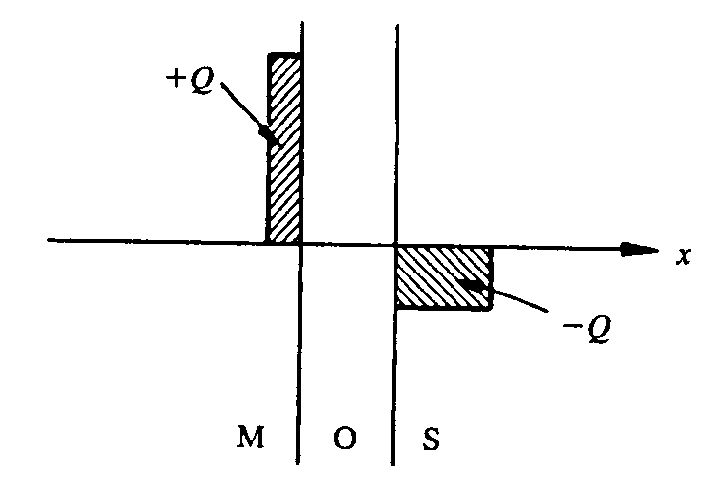
理想MOS电荷块图
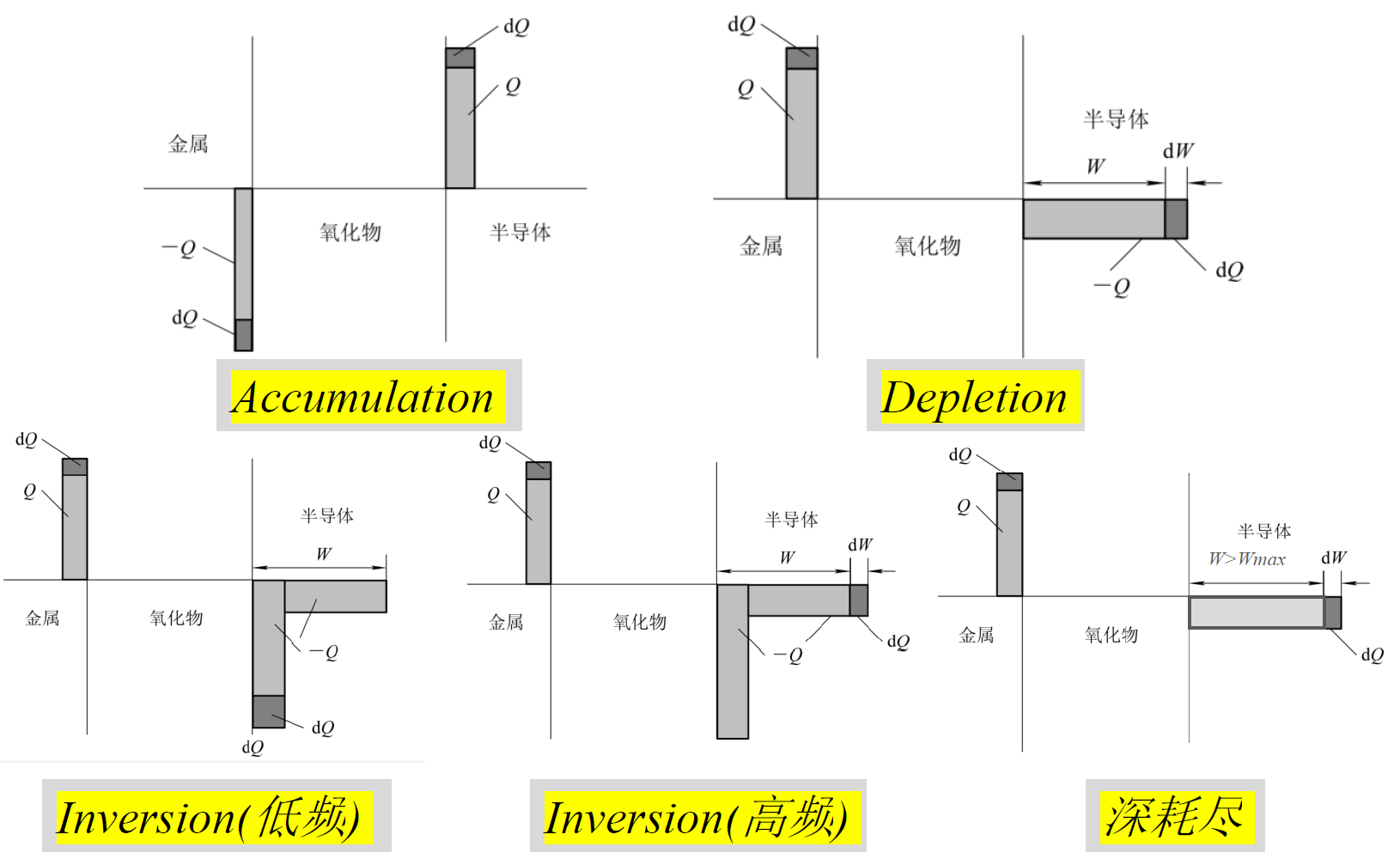
- 平衡条件下在理想MOS结构中任何地方都没有电荷
- 当在MOS电容上加电压后,在金属–氧化层附近的金属中以及氧化层-半导体界面处会出现电荷
- 金属表面积累的电荷设为 $Q_m$,半导体内的空间电荷设为 $Q_s$
- 半导体中自由载流子密度要低得多,对应 $Q_s$ 电荷量需要分布在一定厚度的表面层内,这个带电的表面层叫做空间电荷层。
- 方形化分布近似或块近似不是MOS电容中准确的电荷分布,只是一种定性表示
- 由于在金属和半导体内部电场为零,根据高斯定律,在器件中的电荷总和必须为零。因此,在建立电荷块图时,代表正电荷的面积应该与代表负电荷的面积相等。
表面势
半导体表面与体内的电势差为表面势,用 $V_s$ 或者 $\varphi_s$ 表示
注意“s”是“surface”,surface指半导体与氧化物的界面处😅
| #1 | #2 | #3 | #4 | |
|---|---|---|---|---|
| 半导体类型 | p型 | p型 | n型 | n型 |
| 偏置电压 $V_{g}$ | + | - | + | - |
| 金属一侧积累电荷 $Q_m$ | + | - | + | - |
| 半导体一侧积累电荷 $Q_s$ | - | + | - | + |
| 表面势 $V_{s}$ | + | - | + | - |
| 能带弯曲 | ↓ | ↑ | ↓ | ↑ |
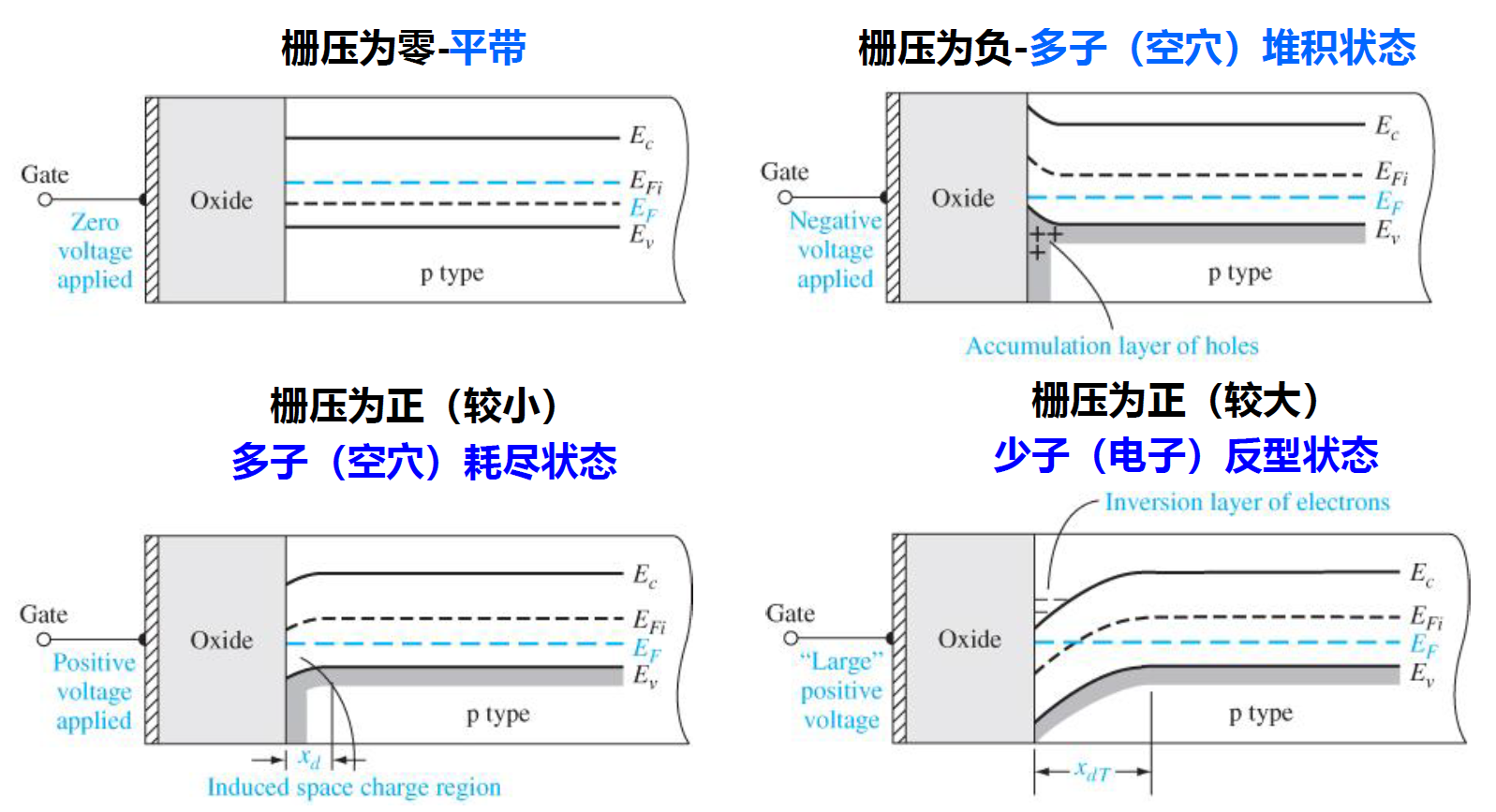
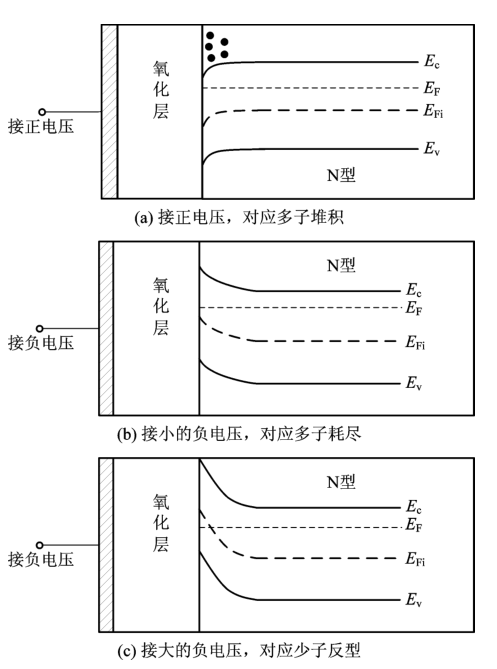
理想MOS能带弯曲
- 假设在正常工作情况下,MOS 电容背面接地,$V_{\mathrm{G}}$ 定义为加到栅上的直流偏置。
- 当 $V_{\mathbf{G}} \neq 0$ 时,注意到首先半导体中的费米能级不受偏置的影响,而且随位置变化保持不变。这是由于假设在所有静态偏置条件下没有电流流过器件导致的;其次,半导体体内始终保持平衡,与 MOS 电容栅上加电压与否无关。
- 如同 $p n$ 结一样,所加偏置会引起器件两端费米能级分开 $q V_{G}$,即由于器件的背接触接地,因此半导体一边的能级在位置上是固定的,而金属一边的能级当 $V_{\mathrm{G}}>0$ 时向下移动,当 $V_{\mathrm{G}}<0$ 时向上移动。
- 从另外一个角度来看,$V_{\mathrm{G}} \neq 0$ 会导致器件内部的电势差,引起 $E_{\mathrm{c}}\left(E_{\mathrm{v}}\right)$ 能带弯曲
- 由于金属是等势区,金属中没有能带弯曲
- 在氧化层和半导体中,当 $V_{\mathrm{G}}>0$ 时能带应向上倾斜(从栅到背接触方向电场增加),而 $V_{\mathrm{C}}<0$ 时能带会向下倾斜
- 在氧化层中利用泊松方程,并假设氧化层是一个理想绝缘体,没有载流子或电荷中心,可以得到 $\mathrm{d} \mathscr{E}_{\mathrm{oxide}} / \mathrm{d} x=0$,$\mathscr{E}_{\mathrm{oxide}}=$ 常数,因此在氧化层中能带倾斜的斜率是一个常数
- 在半导体中的能带弯曲在函数形式上就更为复杂,但由理想情况假设,在能带达到背接触之前能带弯曲应该消失(即 $\mathscr{B} \rightarrow 0$)
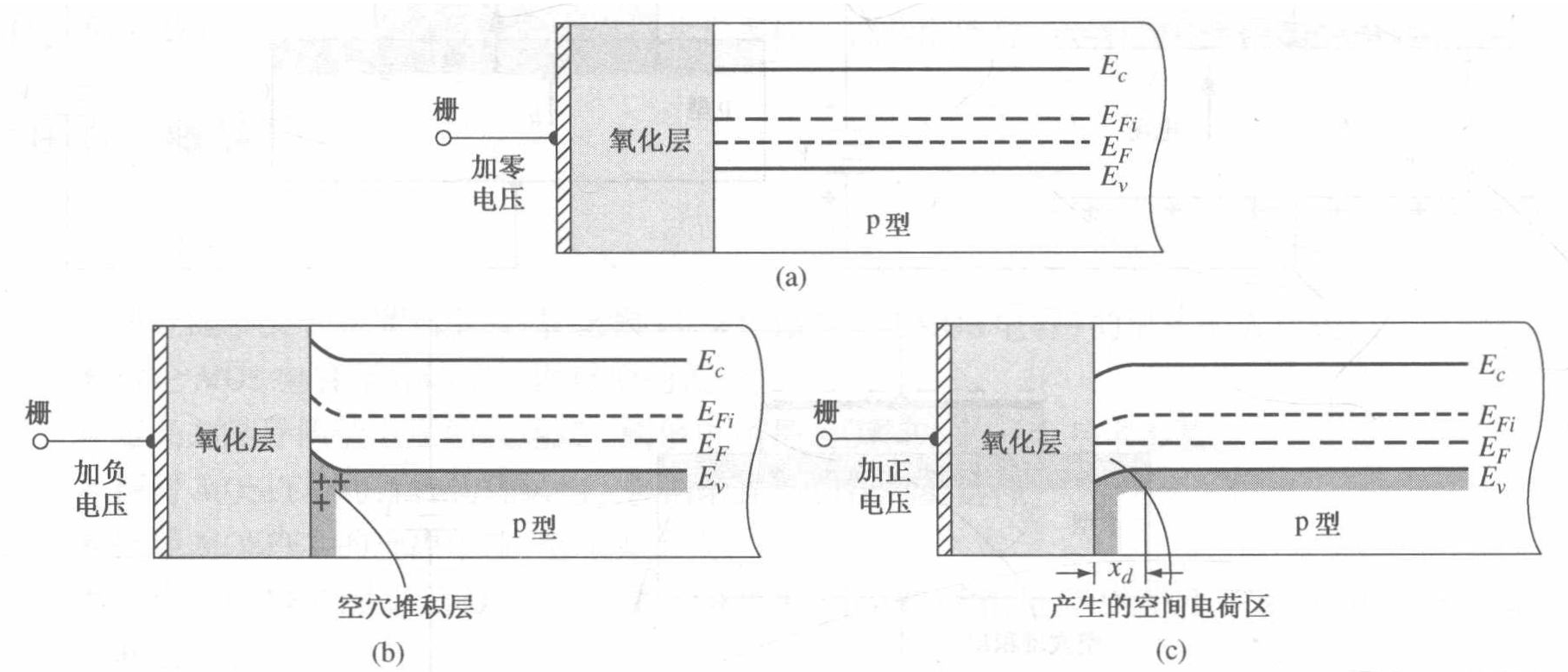
n型正偏置(积累)
假设硅衬底为 $n$ 型,首先考虑正偏置情况,$V_{\mathrm{G}}>0$ 会使金属中的 $E_{\mathrm{F}}$ 相对半导体中的 $E_{\mathrm{F}}$ 降低,导致在绝缘体和半导体中能带有正的倾斜斜率。由图可以推断出在半导体中的电子浓度 $n=n_{\mathrm{i}} \exp \left[\left(E_{\mathrm{F}}-E_{\mathrm{i}}\right) / k T\right]$ 由体内向氧化层-半导体界面增加,这种在氧化层-半导体界面附近多数载流子浓度大于半导体体内浓度的情况一般称为积累。
从电荷的角度来看,当 $V_{\mathrm{G}}>0$ 时,MOS 电容栅上有正电荷。为了保持电荷平衡,必须将带负电的电子吸引到半导体-绝缘体界面。这样得到的结论与前面用能带图得到的一样,因此可以近似得到器件中电荷与位置的函数。
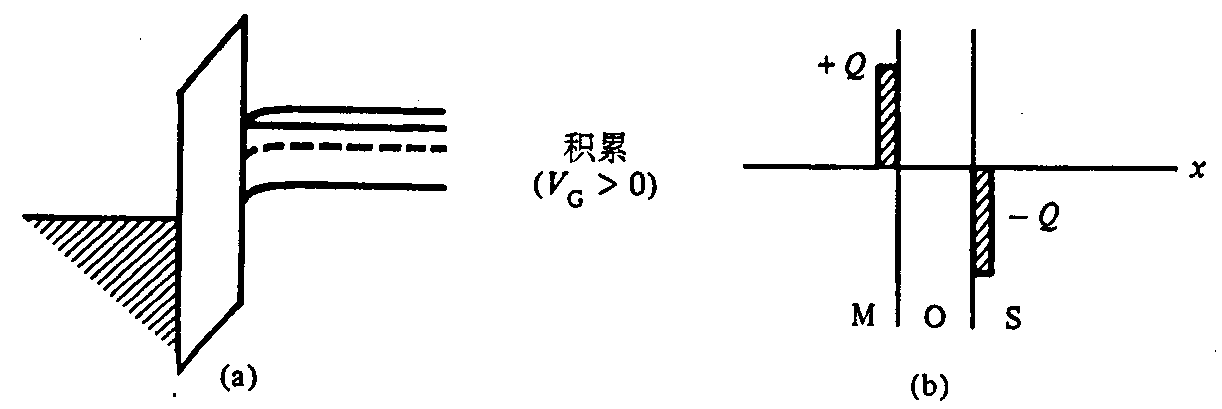
n型较小负偏置(耗尽)
下面考虑 MOS 电容栅上加较小的负偏置的情况,较小的 $V_{\mathrm{G}}<0$ 会使金属中的 $E_{\mathrm{F}}$ 相对半导体中 $E_{\mathrm{F}}$ 稍有升高,在绝缘体和半导体中能带将向较小的负向倾斜,作为多数载流子的电子的浓度在氧化层一半导体界面附近降低,电子被耗尽。
从电荷的角度考虑也可以得到类似的结论,$V_{\mathrm{G}}<0$ 意味着在栅上加了负电荷,会将电子从氧化层半导体界面排斥开,留下带正电的施主杂质离子。氧化层-绝缘层界面处电子和空穴浓度均小于背景掺杂浓度 $N_{\mathrm{A}}$、$N_{\mathrm{D}}$,显然可以称为耗尽情况。
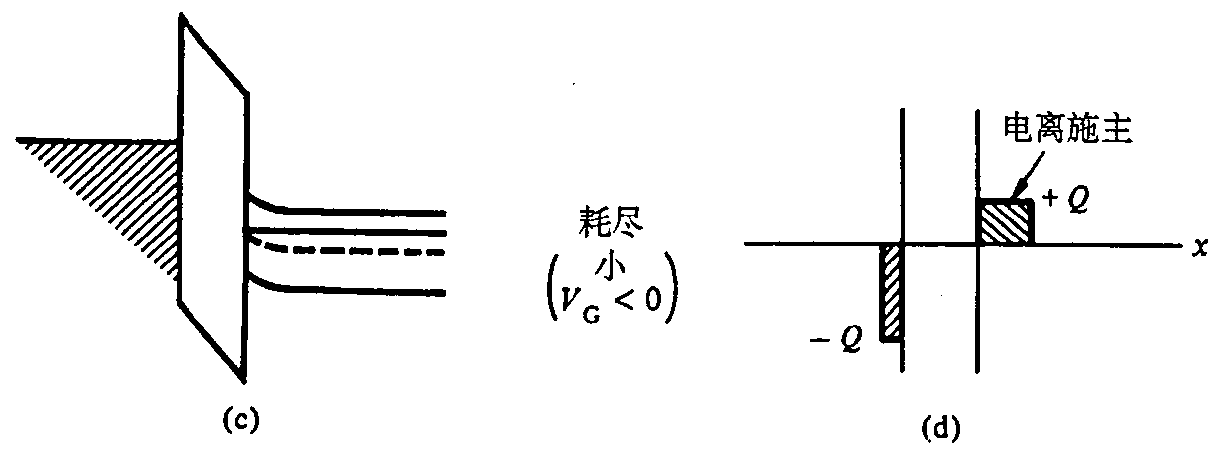
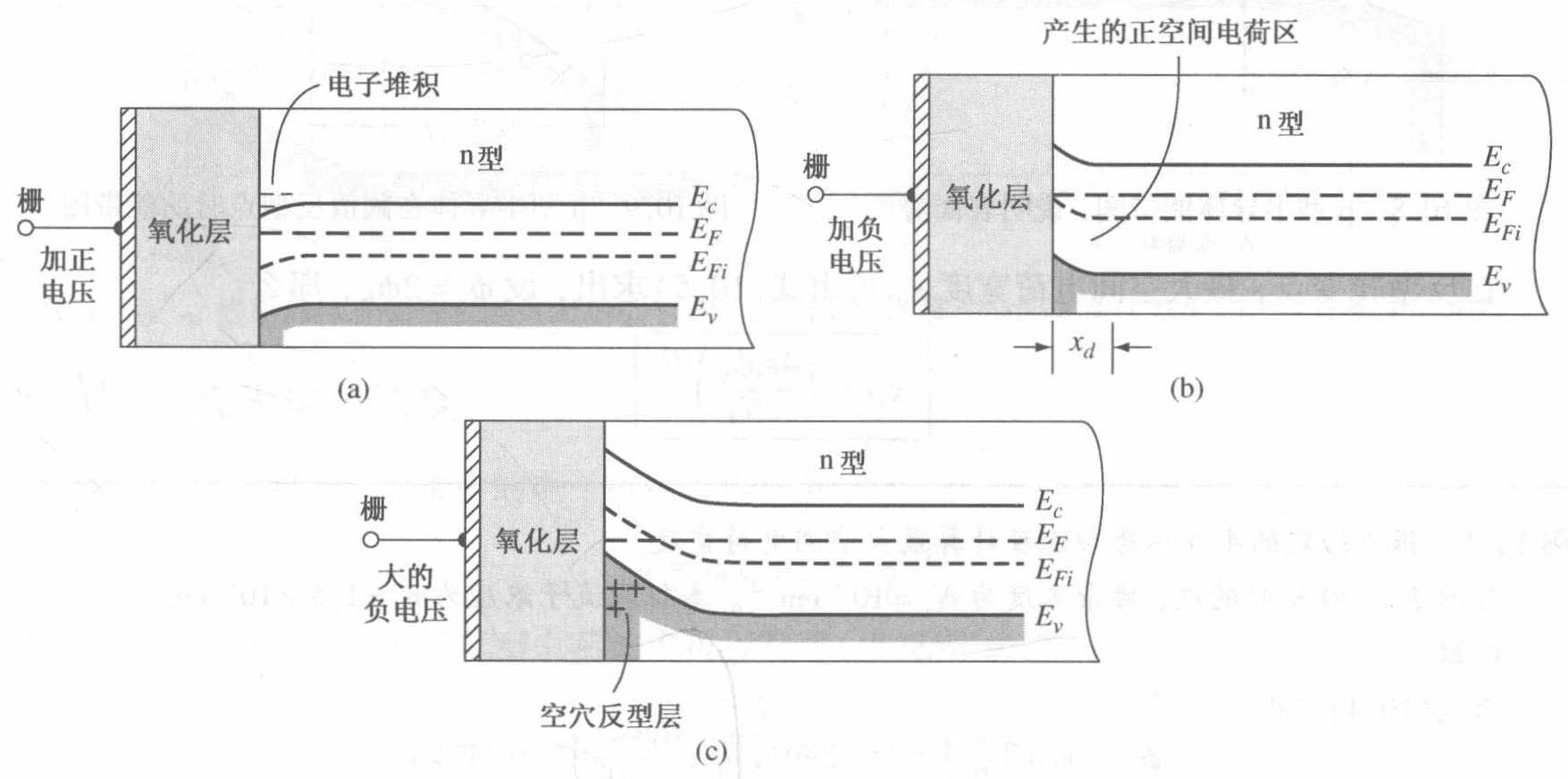
n型较大负偏置(反型)
最后,假设在 MOS 电容栅上加越来越大的负偏置。随着 $V_{\mathrm{G}}$ 继续负向增大,在半导体表面处能带会越来越弯曲,在表面的空穴浓度 $\left(p_{\mathrm{s}}\right)$ 将持续地增加,从小于 $n_{\mathrm{i}}$(对应于表面 $E_{\mathrm{i}}<E_{\mathrm{F}}$)到等于 $n_{\mathrm{i}}$(对应于表面 $E_{\mathrm{i}}=E_{\mathrm{F}}$)直到大于 $n_{\mathrm{i}}$(对应于表面 $E_{\mathrm{i}} >E_{\mathrm{F}}$),最终
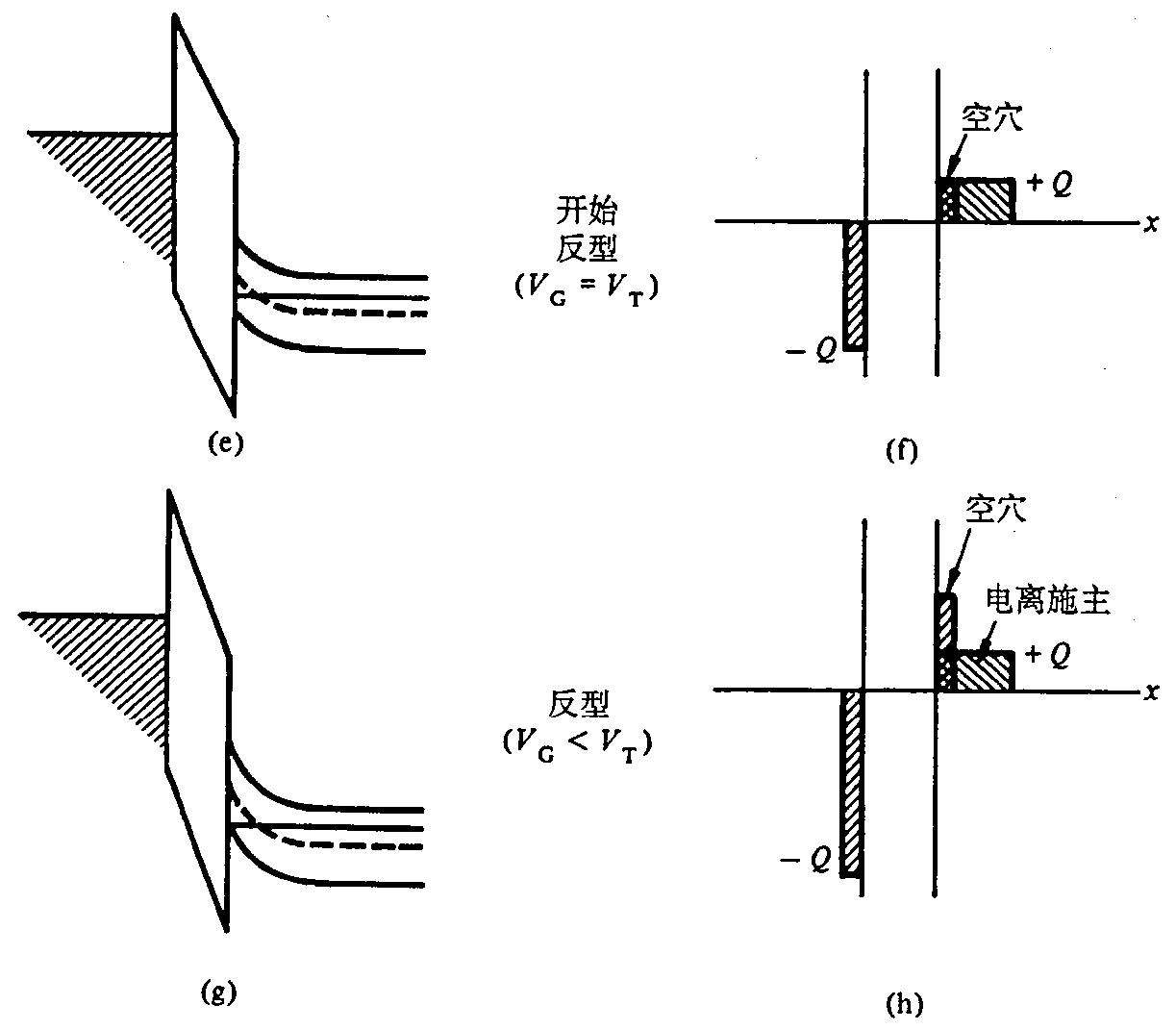
- 开始反型时,表面处的电子浓度等于体内的空穴浓度。这种情况称为阈值反型点,所加的电压称为阈值电压 $V_T$。
- 很明显,当 $V_{\mathrm{G}}=V_{\mathrm{T}}$、$p_{\mathrm{s}}=N_{\mathrm{D}}$ 时,表面不再耗尽。
- 而且当进一步增加负偏置 $\left(V_{\mathrm{G}}<V_{\mathrm{T}}\right)$ 时,$p_{\mathrm{s}}$ 将超过 $n_{\mathrm{bulk}}=N_{\mathrm{D}}$,表面区域的性质将从 $n$ 型变为 $p$ 型。与所观察到的特性变化相一致,$V_{\mathrm{G}}<V_{\mathrm{T}}$ 的情况下,表面少数载流子浓度超过衬底多数载流子浓度,这种情况称为反型。
- 反型时,表面处导带的变化只是栅压的函数。然而,表面电子浓度是表面势的指数函数。表面势每增加数伏特,将使电子浓度以 $10$ 的幂次方增加,但是空间电荷宽度几乎不改变(e的负指数级别,看成不变)。在这种情况下,空间电荷区已经达到了最大宽度。
- 在反型转变点,最大空间电荷宽度 $x_{d T}=\left(\frac{4 \epsilon_{s} \phi_{f p}}{e N_{a}}\right)^{1 / 2}$,其中 $\phi_{f p}$ 是 $E_{F i}$ 和 $E_{F}$ 之间的势垒高度(正数),$\epsilon_{s}$ 是半导体的介电常数,$N_{a}$ 是杂质受主浓度
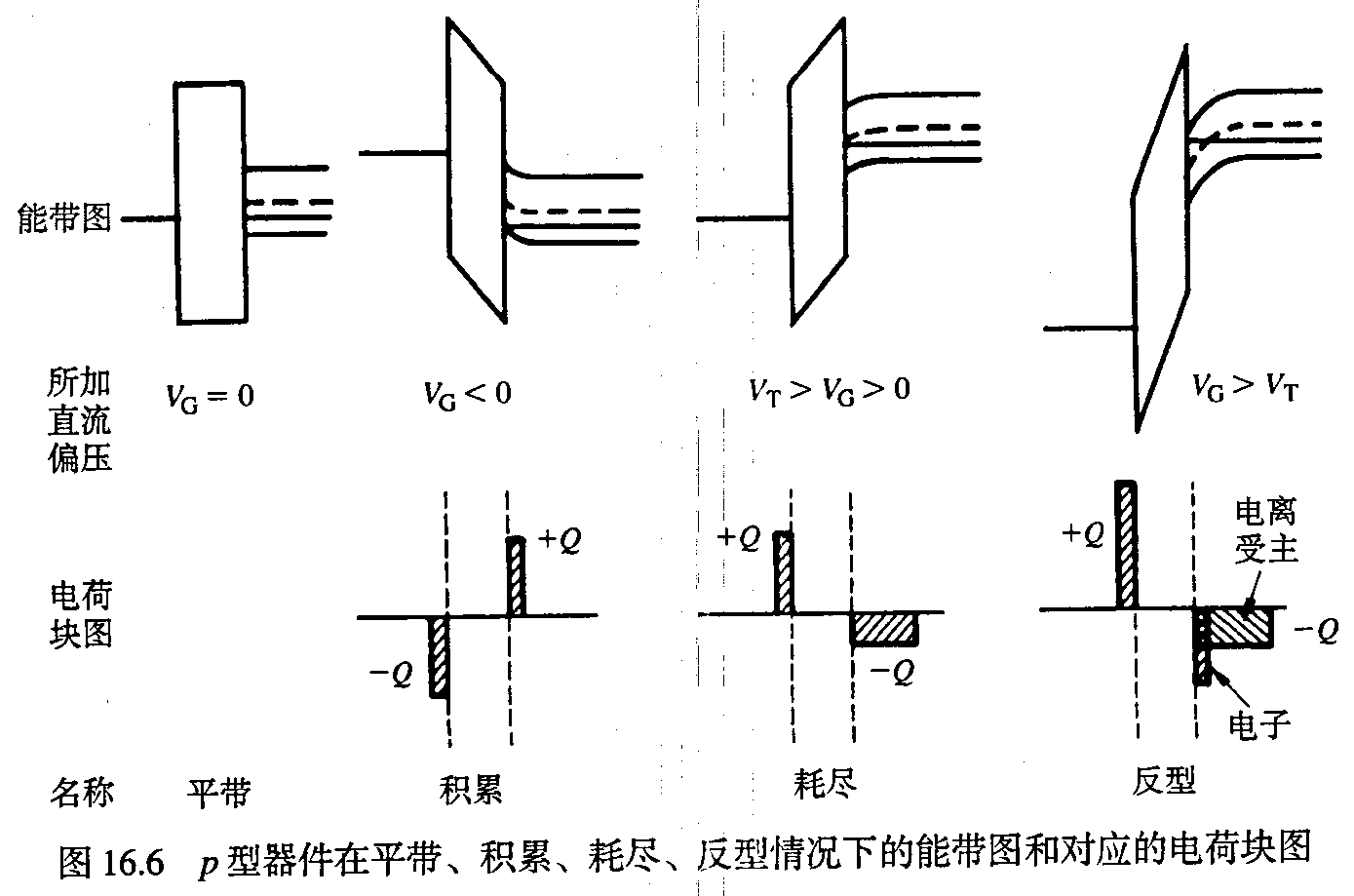
总结
总之,我们现在可以区分出三个物理上截然不同的偏置区一积累、耗尽、反型。对于理想 $n$ 型器件,$V_{\mathrm{G}}>0$,出现积累;$V_{\mathrm{T}}<V_{\mathrm{G}}<0$,出现耗尽;$V_{\mathrm{G}}<V_{\mathrm{T}}$,出现反型。对于 $p$ 型器件简单地将电压极性变反即可。当 $V_{\mathrm{G}}=0$ 时,半导体中没有能带弯曲或称为“平带”,可以标为积累和耗尽之间的分界线。$V_{\mathrm{G}}=V_{\mathrm{T}}$ 的分界线可以简单地称为耗尽-反型过渡点。
n型
空间电场
对于一维 p 型半导体
如果令 F 函数
德拜长度
于是电场可以表示为
表面势为正,能带下弯,电场指向半导体内部为正方向
空间电荷密度
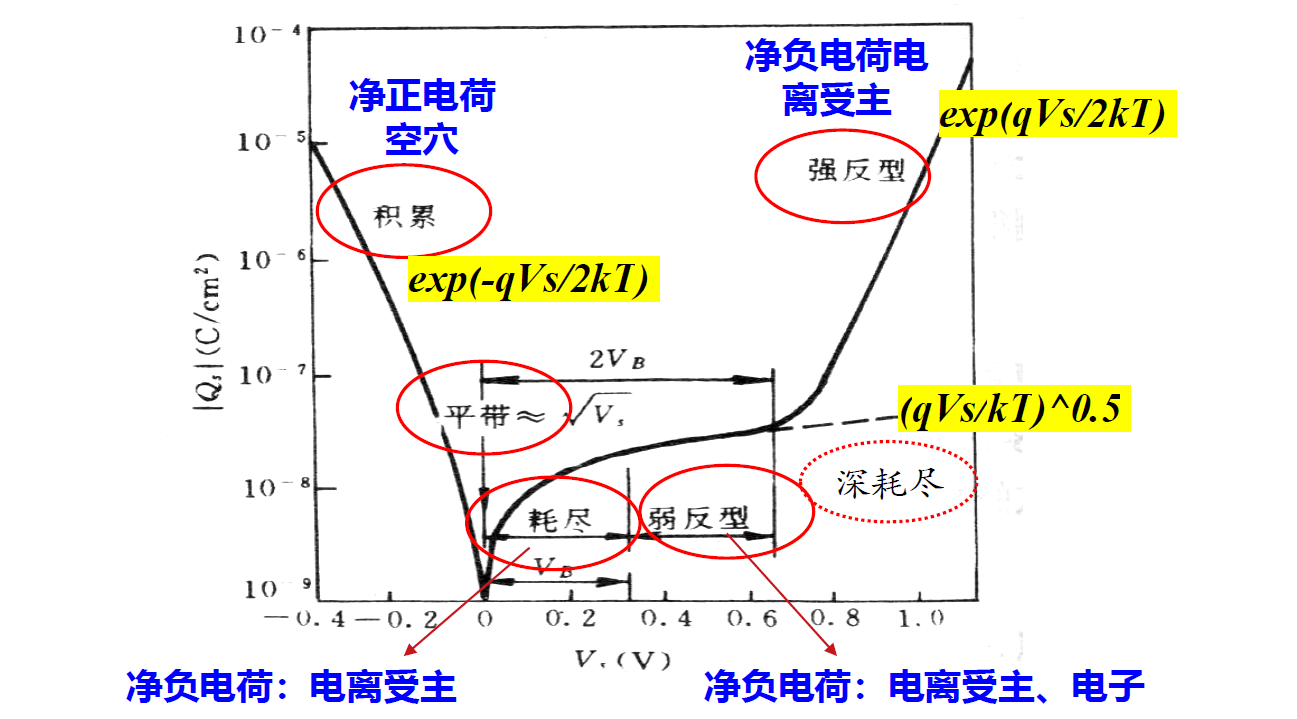
平带($V_g=0$)
积累($V_g<0$)
此时 $\frac{n_{p 0}}{p_{p 0}}\Rightarrow 0$,$V_s<0$,化简得
耗尽($V_g>0$)
此时 $\frac{n_{p 0}}{p_{p 0}}\Rightarrow 0$,$V_s$ 大于 $0$ 但是接近 $0$,化简得
弱反型($2V_B>V_s>V_B$)
同上
强反型($V_s>2V_B$)
同上
深耗尽(非平衡)
能带图
金属-半导体功函数差
平带电压
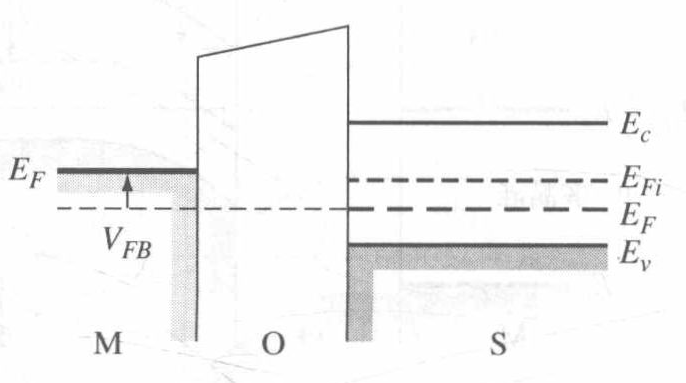
平带电压的定义为当半导体内没有能带弯曲时所加的栅压,此时净空间电荷为零。由于功函数差和在氧化物中可能存在的陷阱电荷,此时穿过氧化物的电
压不一定为零。
氧化物中的净固定电荷在位置上表现得十分靠近氧化物-半导体界面。在我们对 MOS 结构的分析中将假设单位面积的等价陷阱电荷 $Q_{s s}^{\prime}$ 位于氧化物中且直接与氧化物一半导体界面相邻。这时,我们将忽略任何其他可能存在于器件中的氧化物类型的电荷。参数 $Q_{s s}^{\prime}$ 通常称为单位面积电荷数。于是 MOS 器件的平带电压
其中 $C_{\mathrm{ox}}$ 为单位面积的栅氧化层电容
$V_g$ 与 $V_s$ 的关系
在理想结构中,$V_{G}$ 部分降落在氧化层中,部分降落在半导体中,用符号来表示,有
在理想绝缘体中没有载流子或电荷中心,因此有
其中 $x_{\mathrm{o}}$ 为氧化层厚度
对于垂直于两种不同材料之间界面的电场,根据大家熟知的边界条件,有
其中 $D=\varepsilon E$ 是电位移矢量,$Q_{\mathrm{O}-\mathrm{S}}$ 是界面处单位面积电荷,由于理想结构中 $Q_{\mathrm{O}-\mathrm{S}}=0$,有
其中 $K_{\mathrm{S}}$ 是半导体介电常数,$K_{\mathrm{O}}$ 是氧化层介电常数,$\mathscr{E}_{\mathrm{S}}$ 是氧化层-半导体界面处半导体中的电场
在半导体作高斯面,包围住所有电荷,可得
即
代回可得
其中 $C_O$ 是绝缘层的单位面积电容
最终得到
另一方面,$\mathscr{E}_{\mathrm{S}}$ 可以看成是一个已知的 $V_{\mathrm{S}}$ 的函数,由耗尽近似可得
于是
MOSCAP 电容
其中
上式表明 MOSCAP 结构电容相当于绝缘层电容和半导体空间电荷层电容的串联。
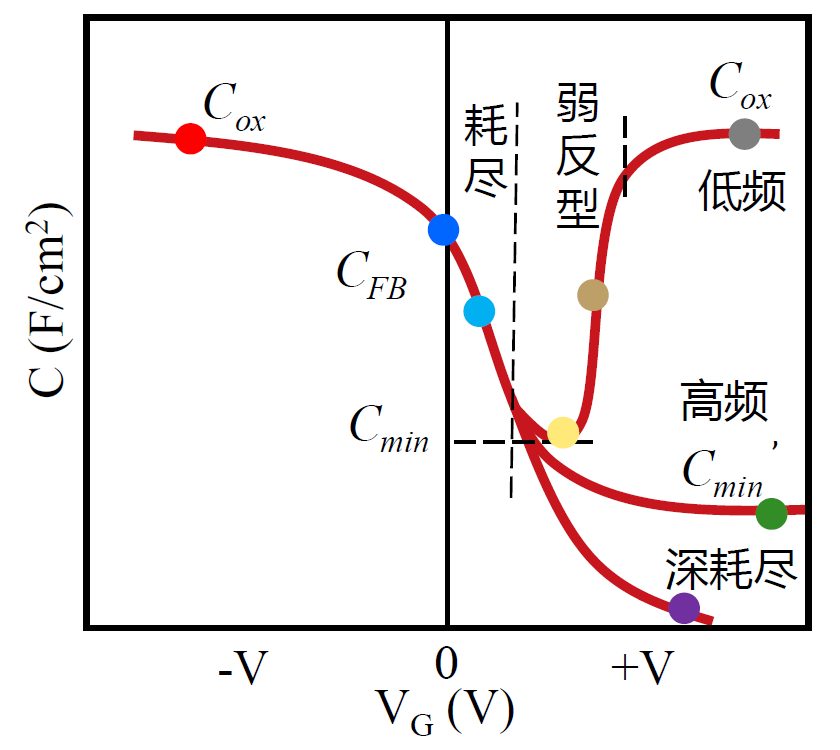
阈值电压和其表面势的关系
非理想效应(四种缺陷)
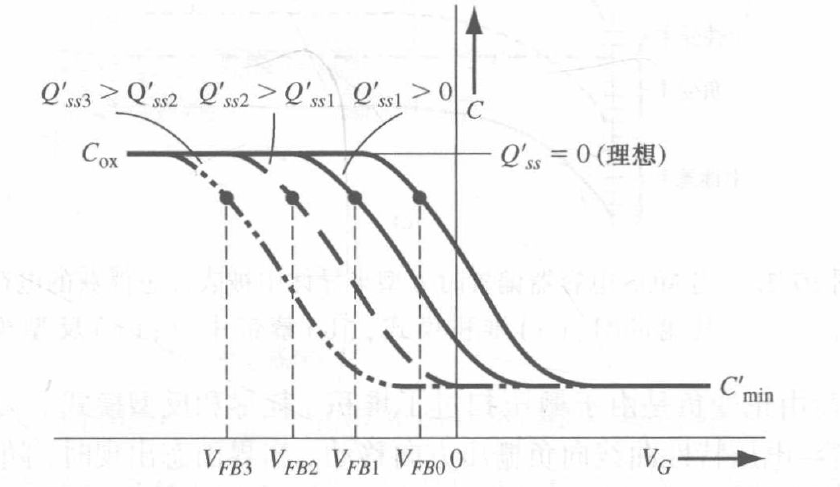
固定栅氧化层电荷
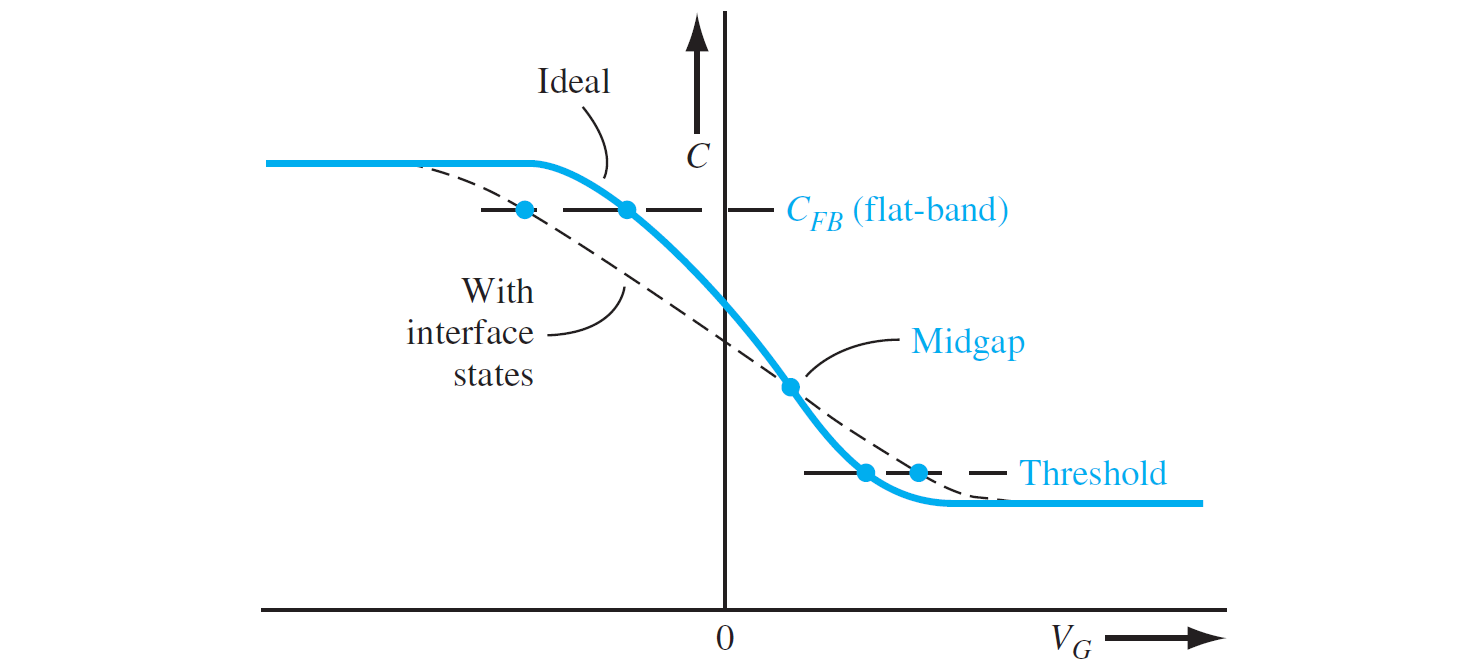
电容-电压特性曲线可用来确定等价固定氧化层电荷。对于给定的 $MOS$ 结构,$\phi_{ms}$ 和 $C_{ox}$ 是已知的,所以理想平带电压和平带电容可以求出。平带电压的实验值可以从电容-电压特性曲线测出,从而固定氧化层电荷能够被确定。电容-电压测量方法是表征 MOS 器件很有用的判别工具。
固定栅氧化层电荷会使得C-V曲线向左或向右平移,具体取决于电荷的正负性和大小。
- 如果固定栅氧化层电荷为正,那么C-V曲线会向左平移,表示需要更小的栅压才能使半导体表面反型
- 如果固定栅氧化层电荷为负,那么C-V曲线会向右平移,表示需要更大的栅压才能使半导体表面反型
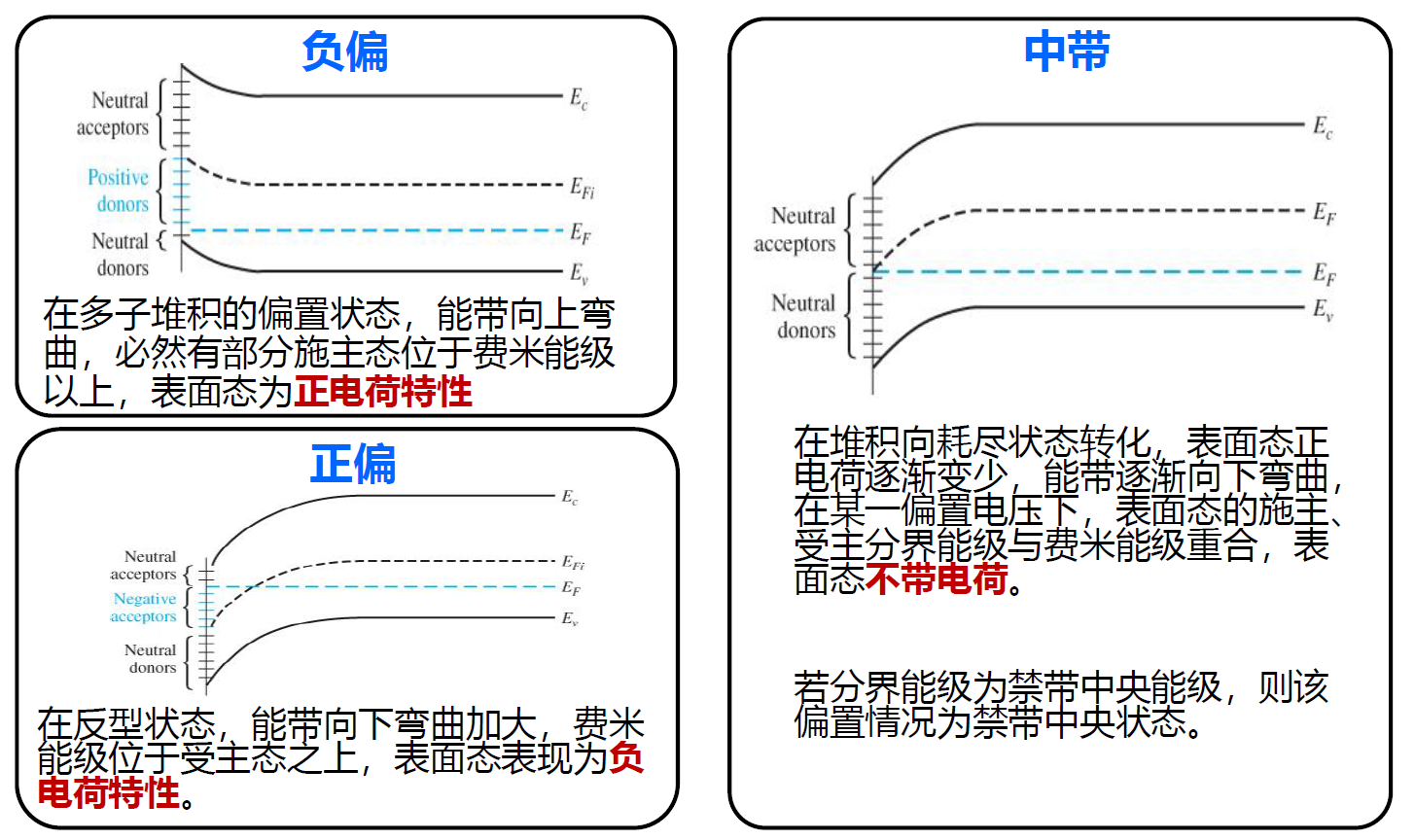
界面陷阱电荷
半导体在界面处周期性突然中止,以便允许的电子能级存在于禁带中。这些允许的能态称为界面态。与固定氧化层电荷相比,电荷在半导体和界面态之间流动。这些界面态中的净电荷是带隙中费米能级位置的函数。
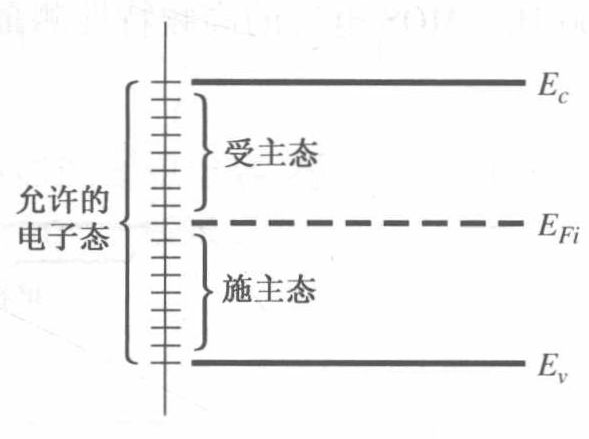
通常,受主态存在于能带的上半部分,而施主态存在于能带的下半部分。若费米能级低于受主态,那么受主态是中性的,一旦费米能级位于其上时它将是负电性的。若费米能级高于施主态,那么施主态是中性的,一旦费米能级位于其下时它将是正电性的。因此界面电荷是 MOS 电容器栅压的函数。
界面态使得C-V曲线变得更加平坦
氧化层中可动电荷
氧化层中可动电荷是指在氧化层内部或表面可以移动的离子电荷,通常是由钠离子或其他杂质离子组成的。
氧化层中陷阱电荷
氧化层中陷阱电荷是指在氧化层内部存在的能够俘获或释放载流子的缺陷电荷,通常是由辐射、热载流子注入或其他工艺引起的。
计算题解题步骤
- 先算 $V_B$
$V_B=\frac{kT}{q}\ln\left(\frac{N_{A \text{or} D}}{n_i}\right)$ - 算平带电压
- 算阈值电压
MOSFET
结构与参数
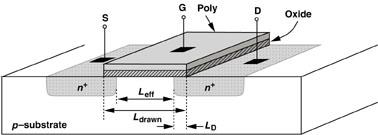
- 电场调节作用
- 多子器件
- 一种载流子(单极)
- 输入阻抗高
- 电压控制器件
- 噪声低,抗辐射能力强
- 工艺要求高
- 频率范围小,功耗低
- 集成度高
分类
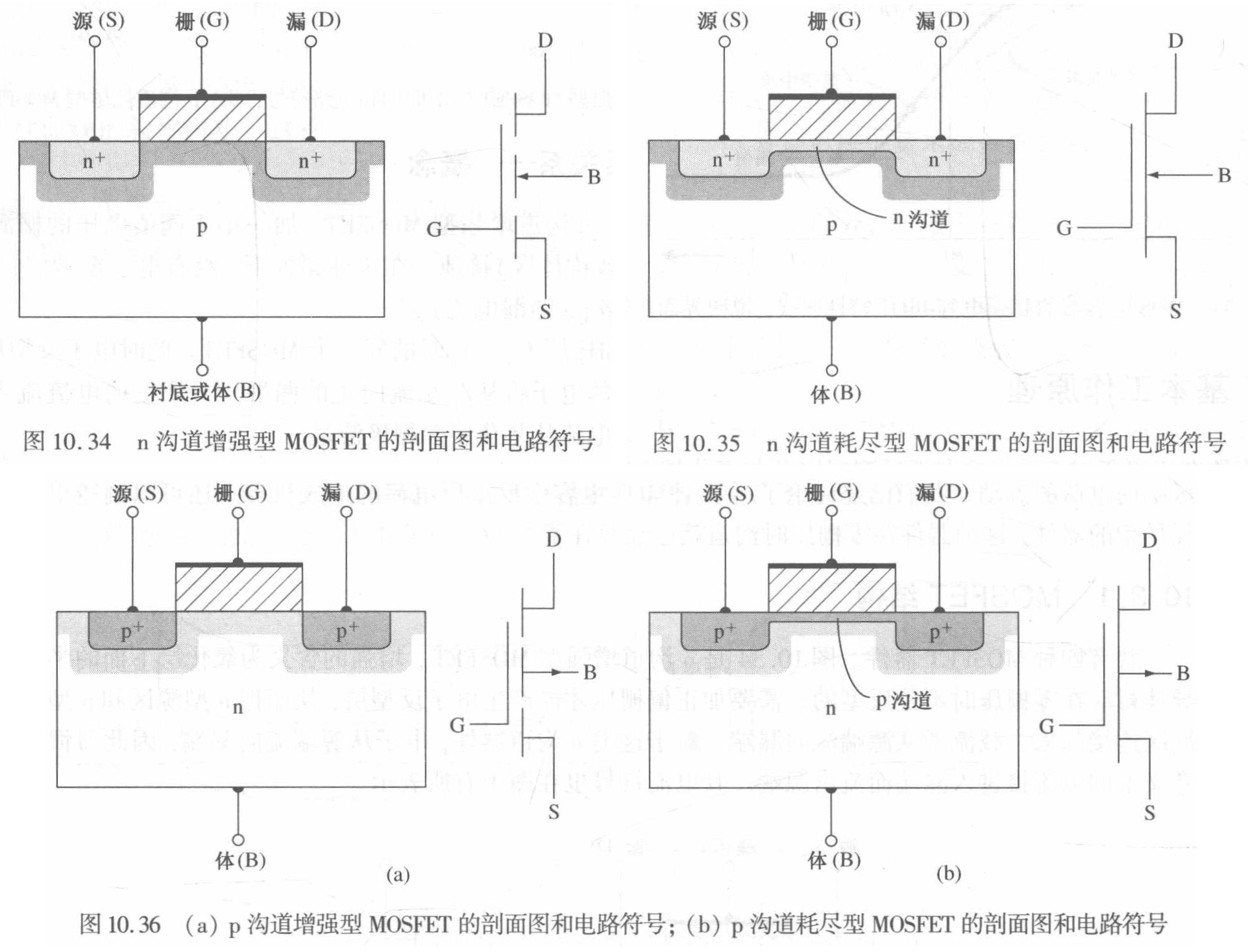
共有四种 MOSFET 器件。
- 图 10.34 是 n 沟道增强型 MOSFET。增强的含义为氧化层下面的半导体衬底在零栅压时不是反型的。需要加正偏栅压才能产生电子反型层,从而把 n 型源区和 n 型漏区连接起来。载流子从源端流向漏端。对于这类 n 沟道器件,电子从源端流向漏端,因此习惯意义上的电流将进入漏端而流出源端。其电流符号也在图中有所表示。
- 图 10.35 是 n 沟道耗尽型 MOSFET。栅压为零时氧化层下面已经存在 n 型沟道区。我们已经知道 p 型衬底 MOS 器件的阈值电压可以为负,这意味着在零栅压时电子反型层已经存在了。这种器件也被认为是耗尽型器件。图中的 n 沟道可以是电子反型层或是特意掺杂的 n 区。n 沟耗尽型 MOSFET 的习惯意义上的电流符号如图 10.35 所示。
- 图 10.36(a) 和图 10.36(b) 分别为 p 沟道增强型 MOSFET 和 p 沟道耗尽型 MOSFET。在 p 沟道增强型器件中,必须加负栅压才能产生空穴反型层,从而连接 p 型的源区和漏区。空穴从源流向漏,因此习惯上的电流将流入源区而流出漏区。零栅压时耗尽型器件已经存在 p 沟道区了。电流符号如图 10.38 所示。
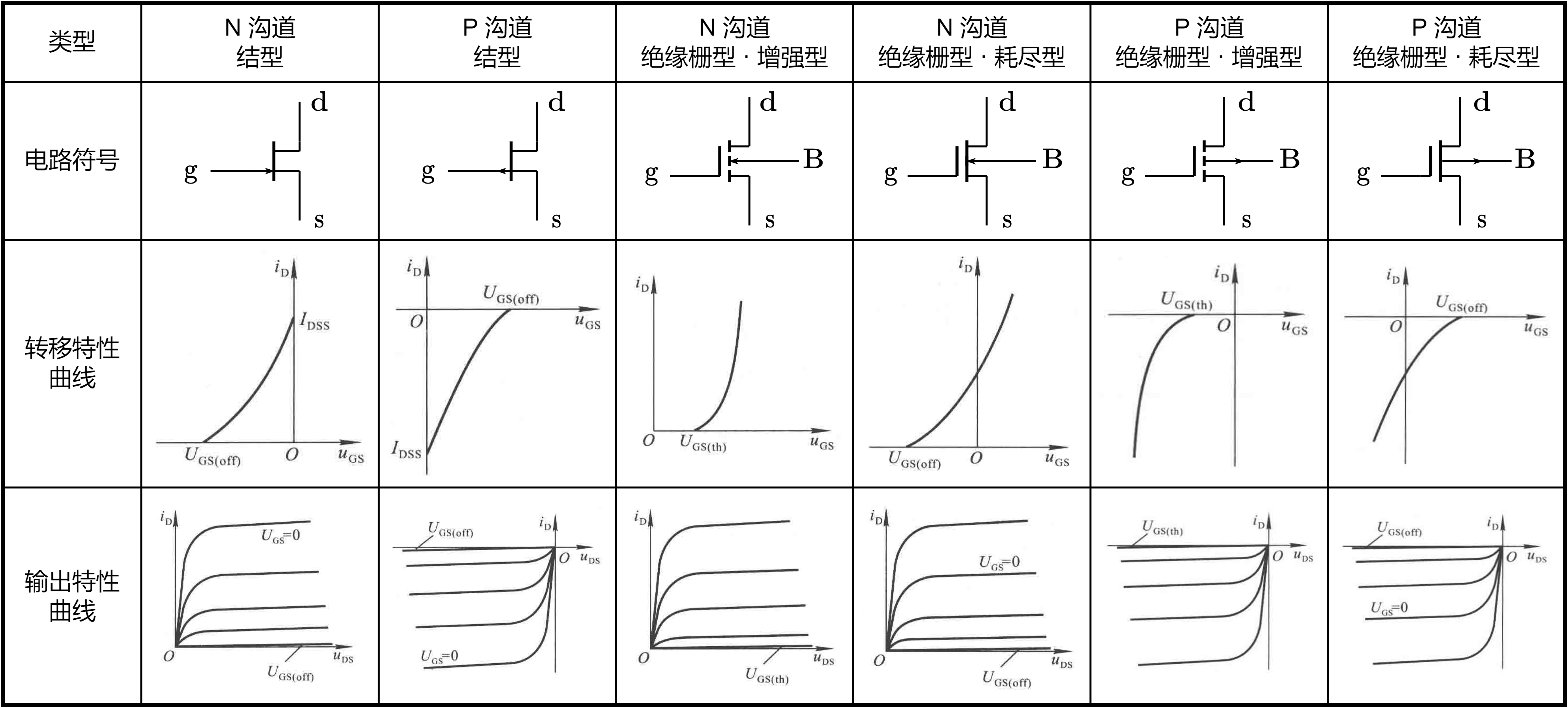
| NMOSFET | PMOSFET | |
|---|---|---|
| 衬底掺杂 | p | n |
| 源漏掺杂 | n | p |
| 源端 | 接衬底 | 接衬底 |
| 漏端 | 接正电压 | 接负电压 |
| 电流流向 | D->S | S->D |
| 沟道载流子 | 电子 | 空穴 |
| 载流子运动方向 | S->D | S->D |
| NMOS增强型 | NMOS耗尽型 | PMOS增强型 | PMOS耗尽型 | |
|---|---|---|---|---|
| 阈值电压 | 大于0 | 小于0 | 小于0 | 大于0 |
| 工作区域 | $V\ge V_T$ | $V\ge V_T$ | $V\le V_T$ | $V\le V_T$ |
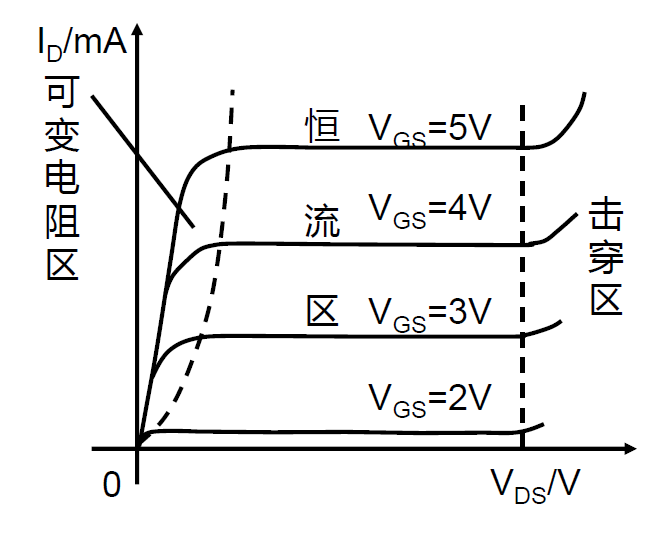
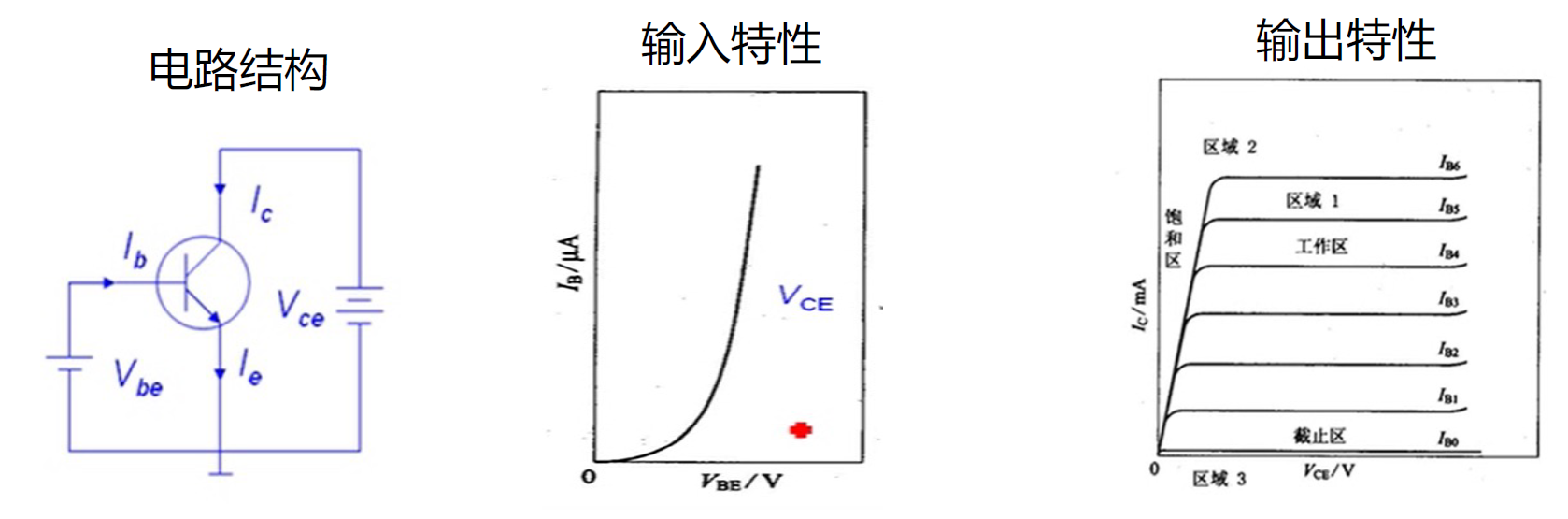
电流电压关系(输出特性)
通断
- 对于 n 沟道增强型 MOSFET,加一小于阈值电压的栅源电压以及一非常小的漏源电压。源和衬底(或称体区)接地。在这种偏置下,没有电子反型层,漏到衬底的 pn 结是反偏的,漏电流为零(忽略 pn 结漏电流)。
- 当所加栅压 $V_{GS}>V_{T}$,电子反型层产生了,当加一较小的漏电压时,反型层中的电子将从源端流向正的漏端。习惯上的电流流入漏极而流出源极。在这种理想情况下,没有电流从氧化层向栅极流过。
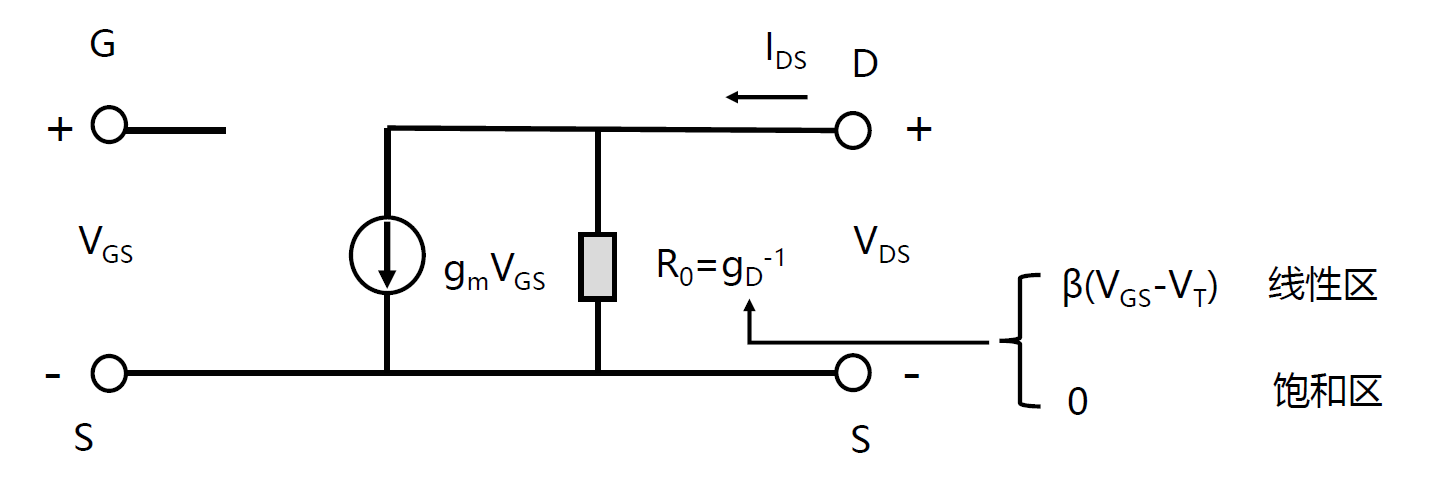
沟道电导
对于较小的 $V_{D S}$,沟道区具有电阻的特性,因此可得:
式中 $g_{d}$ 为在 $V_{D S}$ 趋近于零时的沟道电导。沟道电导可以由下式表达:
式中 $\mu_{n}$ 为反型层中的电子迁移率。$\left|Q_{n}^{\prime}\right|$ 为单位面积的反型层电荷数量。反型层电荷是栅压的函数;因此,基本 MOS 晶体管的工作机理为栅压对沟道电导的调制作用。而沟道电导决定漏电流。我们可以先假设迁移率为一常数
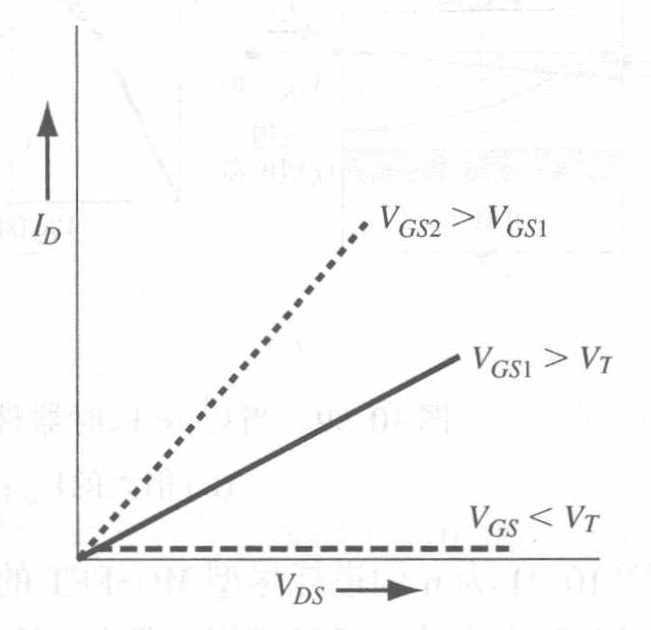
- 当 $V_{GS}<V_{T}$ 时,漏电流为零。
- 当 $V_{GS}>V_{T}$ 时,沟道反型层电荷密度增大,从而增大沟道电导。
- 当 $V_{GS}$ 增大到漏端的氧化层压降等于 $V_{T}$ 时,漏极处的反型层电荷密度为零。此时,漏极处的电导为零,这意味着 $I_{D}-V_{DS}$ 的特性曲线的斜率为零。
- 定义式中 $V_{DS}\text{(sat)}$ 为在漏极处产生零反型层电荷密度的漏源电压。假设沟道长度的变化 $\Delta L$ 相对于初始沟道长度 $L$ 而言很小,那么当 $V_{DS}>V_{DS}\text{(sat)}$ 时漏电流为一常数。
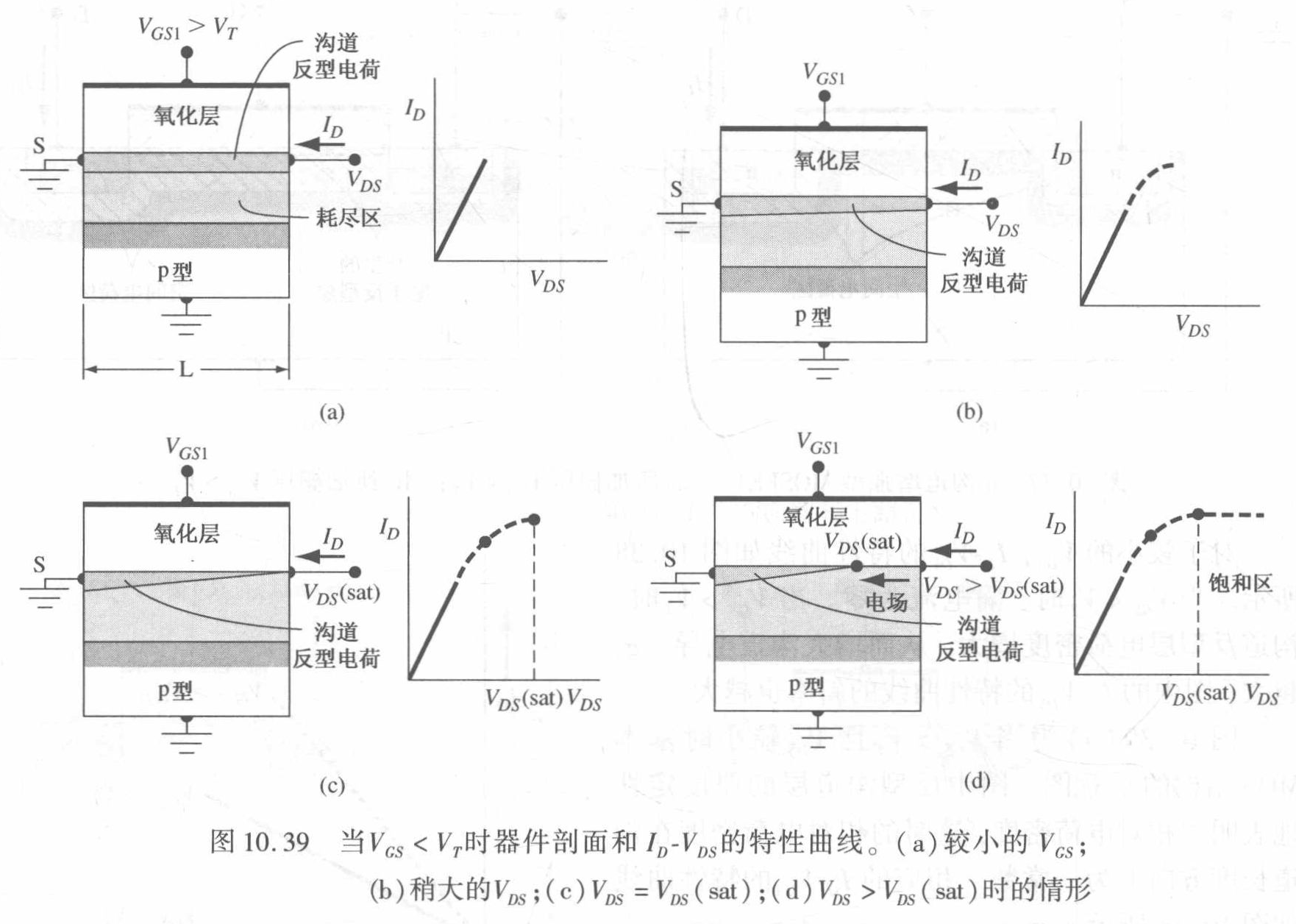
$I_D-V_{DS}/V_{GS}$ 关系
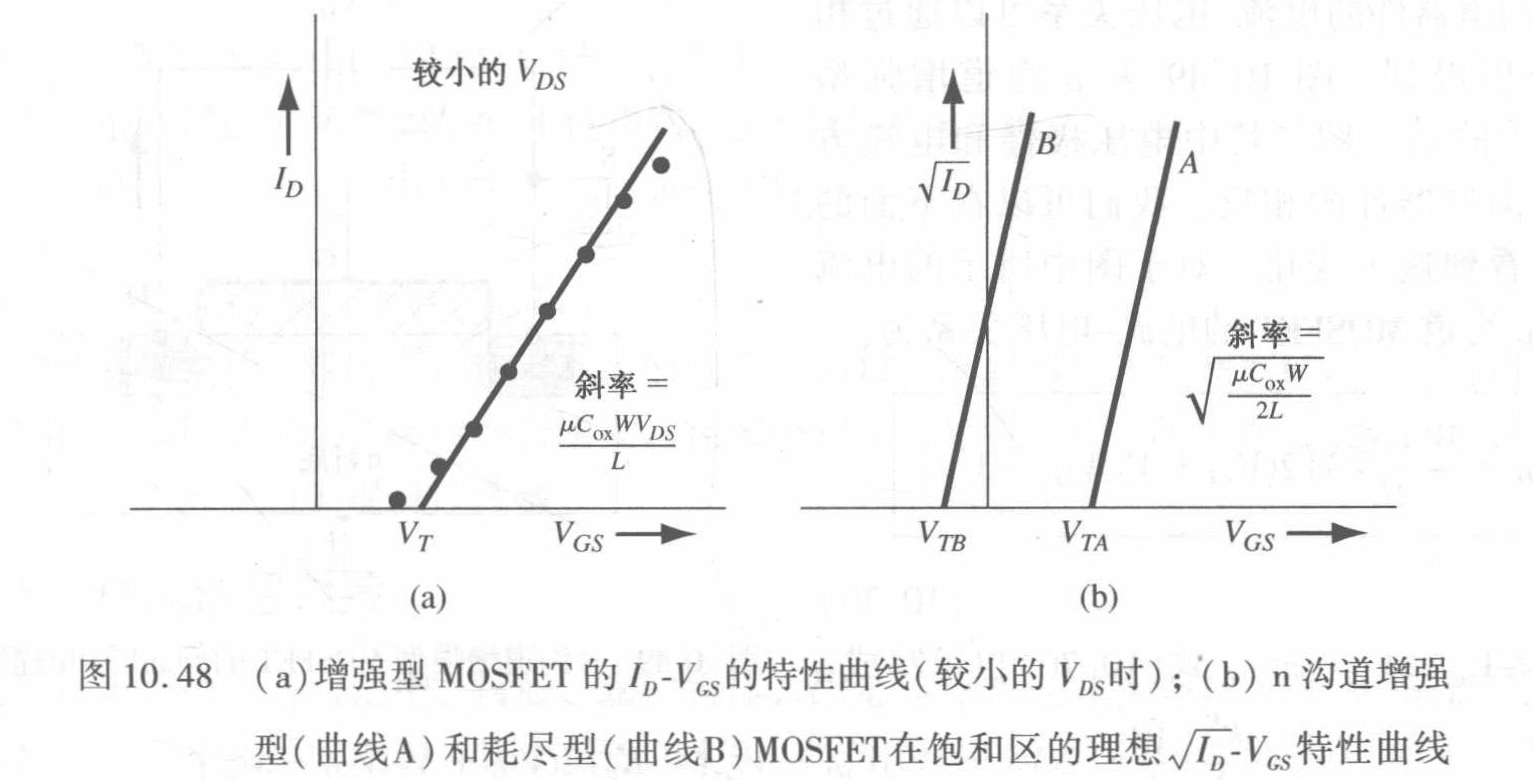
- $I_D-V_{GS}$ 关系中,一条直线可以近似通过图中各点。在低 $V_{GS}$ 值处点与直线的偏离是由于亚阈值电导的影响,在高 $V_{GS}$ 值处,点与直线的偏离是由于迁移率成为栅压的函数。
在非饱和区,n 沟道 MOSFET 的理想电流-电压关系:
在饱和区,理想的电流-电压关系为:
- $k_{n}^{\prime}=\mu_{n} C_{\mathrm{ox}}$ 称为 n 沟道 MOSFET 的器件跨导参数,单位为 $\mathrm{A} / \mathrm{V}^{2}$
- $K_{n}=\left(W \mu_{n} C_{\mathrm{ox}}\right) / 2 L=\left(k_{n}^{\prime} / 2\right) \cdot(W / L)$ 称为 $\mathrm{n}$ 沟道 MOSFET 的器件跨导系数,单位也为 $\mathrm{A} / \mathrm{V}^{2}$
p 沟道 MOSFET 的电流-电压关系为:
在饱和区
- $k_{p}^{\prime}=\mu_{p} C_{\mathrm{ox}}$ 称为 p 沟道 MOSFET 的器件跨导参数
- $K_{p}=\left(W \mu_{p} C_{\mathrm{ox}}\right) / 2 L=\left(k_{p}^{\prime} / 2\right) \cdot(W / L)$ 称为 $\mathrm{p}$ 沟道 MOSFET 的跨导系数
- 源漏饱和电压为 $V_{S D}(\mathrm{sat})=V_{S G}+V_{T}$
定量推导
- 假设
- 沟道中的电流是由漂移而非扩散产生的。
- 栅氧化层中无电流。
- 利用缓变沟道近似,$\partial \mathrm{E}_{y} / \partial y \gg \partial \mathrm{E}_{x} / \partial x$,这个近似意味着 $\mathrm{E}_{x}$ 为一常数。
- 任何固定氧化层电荷等价于在氧化层-半导体界面处的电荷密度。
- 沟道中载流子迁移率为常数。
- 欧姆定律:式中 $\sigma=e \mu_{n} n(y)$ 为沟道电导率,$\mathrm{E}_{x}$ 为漏源电压产生的沟道方向的电场,$\mu_{n}$ 为电子迁移率,$n(y)$ 为反型层中的电子浓度。
- 在 $y$ 和 $z$ 方向上的沟道截面对 $J_{x}$ 进行积分可以得到总沟道电流
- 计算单位面积的反型层电荷(此时为一负值)可以化简总沟道电流其中 $W$ 是沟道宽度
- 根据高斯定理式中 $\epsilon_{\mathrm{ox}}$ 为氧化层介电常数。$Q_{T}$ 为封闭表面中的总电荷,$E_{n}$ 为通过表明 $S$ 电场的向外的分量。总电荷还可以写成:联立得
- 可得(具体见课表)
- 沿沟道长度进行积分,可得上式在 $V_{G S} \geqslant V_{T}$ 且 $0 \leqslant V_{D S} \leqslant V_{D S}\text{(sat)}$ 时成立。
- 当 $V_{D S} > V_{D S}\text{(sat)}$ 时,
阈值电压的调节方法
跨导
MOSFET 的跨导定义为相对于栅压的漏电流的改变,或者写为:
跨导有时也称为晶体管增益。
- 工作在非饱和区的 n 沟道 MOSFET,跨导:在非饱和区,跨导随 $V_{D S}$ 线性变化,而与 $V_{G S}$ 无关。
- 工作于饱和区的 n 沟道 MOSFET,由电流-电压特性得跨导为:在饱和区,跨导随 $V_{G S}$ 线性变化,而与 $V_{D S}$ 无关。
跨导是器件结构、载流子迁移率和阈值电压的函数。随着器件沟道宽度的增加、沟道长度的增加或氧化层厚度的减小,跨导都会增大。在 MOSFET 电路设计中,晶体管的尺寸,尤其是沟道宽度 $W$,是一个重要的工程设计参数。
非理想效应
衬底偏置效应(体效应)
当衬底偏置电压增加时,NMOSFET的阈值电压会减小,而PMOSFET的阈值电压会增大(绝对值都是增大)。这是因为衬底偏置电压会改变沟道区域的电势,影响栅极对沟道的控制能力。
当源-衬底的电压不为 $0$ 时,需要 $V_S=2V_B+V_{SB}$ 才能达到反型条件。定义体效应系数 $\gamma$
因此阈值电压的改变量可以表达为:
非零漏电导效应(沟道长度调制效应)
非零漏电导效应(沟道长度调制效应)是指MOSFET在饱和区工作时,由于漏极电压的增大,导致沟道的夹断点向源极方向移动,使得有效沟道长度减小,从而使漏极电流增大的效应。这个效应会导致MOSFET的电流-电压特性曲线在饱和区上翘,而不是水平的
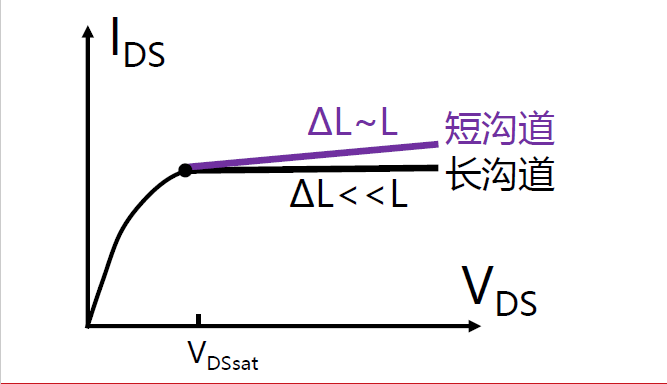
亚阈区现象
MOSFET的亚阈区现象是指MOSFET的栅极电压低于阈值电压时,半导体表面没有形成导电沟道,但仍有一股较小的电流通过器件,称为亚阈电流。这个电流是由源区注入到衬底表面的少数载流子,并扩散到漏区所形成的,本质上是少数载流子的扩散电流。亚阈电流随着栅极电压的增加而指数式增加,其大小与衬底掺杂浓度、半导体表面电容、表面态密度和温度等因素有关。亚阈区工作状态具有低电压和低功耗的优点,在逻辑开关和存储器等大规模集成电路中有重要应用。
弱反型时($V_B<V_{S}<2V_B$)半导体表面浓度低,$I_{DS}$ 与 $e^{qV_s/kT}$ 成正比
亚阈值导电由于其指数级的增长方式,会使得器件会有较大的增益,然而由于其电流较小,使得电路的速度时极其有限的。
定义亚阈摆幅 Subthreshold Swing
- 极限值 60mV/dec
- SS 越小越好,减小 SS 的方法:薄栅HK、轻掺杂、高质量界面
非常数表面迁移率效应
总结:当栅极电压增加时,表面电场也增加,使得载流子与界面发生更多的散射,从而降低了迁移率。当漏极电压增加时,沟道区域的水平电场也增加,使得载流子速度趋于饱和,从而降低了沟道电导率。
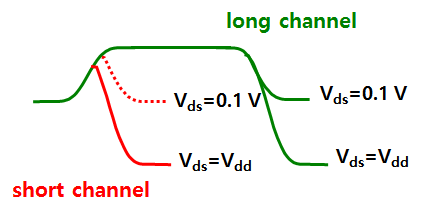
对输出特性的影响
- 线性区:$V_{GS}$ 较小时,斜率增加等间距;$V_{GS}$ 较大时,曲线密集
- 饱和区:$V_{GS}$ 较大时,$I_{D,\text{sat}}$ 随 $V_{GS}$ 增加不按平方规律
对转移特性的影响
$g_m$ 随着电压增加而下降
击穿
- 两种击穿模式:OFF STATE Breakdown;ON STATE Breakdown
- 三种击穿路径:漏-衬底;漏-源;漏-栅极
漏-衬底击穿
- 就是pn结的反向击穿(雪崩击穿),电流几乎快速增大,很容易烧毁器件
- 解决方法:增加耗尽区宽度,如降低掺杂
漏-源击穿
耗尽区碰到源区,源漏之间就不需要开启就形成了通路:源漏势垒穿通
- 穿通击穿的击穿点软,击穿过程中,电流有逐步增大的特征,这是因为耗尽层扩展较宽,产生电流较大。
- 穿通击穿一般不会出现破坏性击穿。
- 穿通击穿一般发生在沟道体内
栅击穿
多晶硅内产生导电细丝
等比例缩小
MOSFET等比例缩小的原则是指在保持器件内部电场强度不变的前提下,将MOSFET的横向尺寸、纵向尺寸以及工作电压按照同一个比例因子k进行缩小,同时提高衬底的掺杂浓度。这样可以提高MOSFET的速度、降低功耗、增加集成密度,同时保证器件的可靠性和热稳定性。这种原则也被称为恒定电场比例缩小或CE准则。
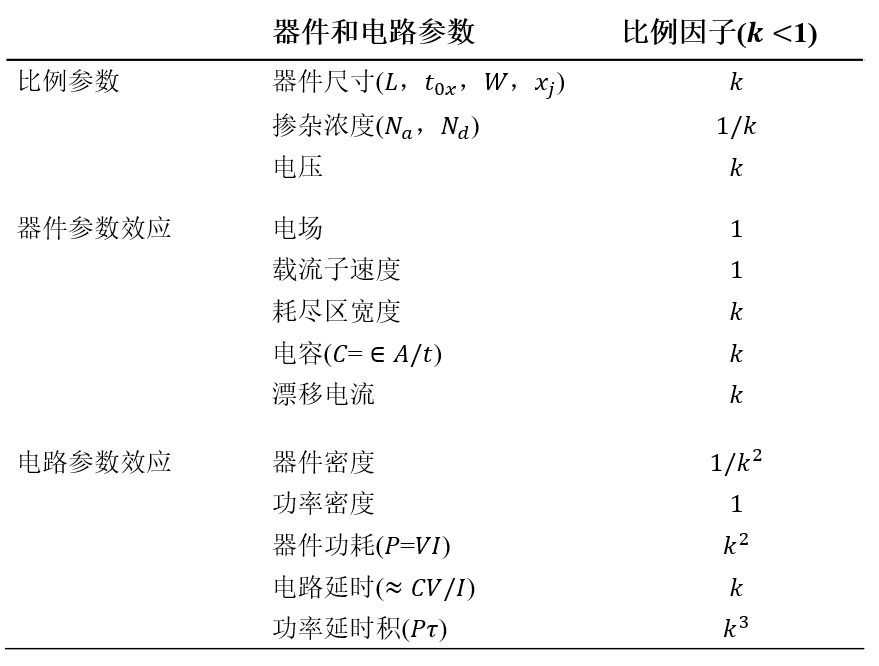
恒定电场:
- 尺寸缩小 k 倍
- 电压降低 k 倍
- 电流 $I_{DS}$ 降低为原来的 k 倍,电流密度增加为原来的 k 倍
- 速度增加 $1/k$ 倍
- 功耗降低 $k^2$
- 电源电压下降,导致电路动态范围及噪声容限减小
- 阈值电压减小,导致较大的亚阈值电流
VT roll-off(短沟道效应)
- 当MOSFET的沟道长度小于3微米时,由于源极和漏极的耗尽层相互影响,沟道区的电势分布不再是一维的,而是二维的。这会导致沟道区的电场增大,载流子的迁移率和速度受到影响。
- 短沟道效应会引起一些不利的现象,如阈值电压 $V_T$ 随沟道长度降低而降低($V_{DS}$ 越高越严重)、漏致势垒降低、亚阈特性退化、热载流子效应等。这些现象会影响MOSFET的性能和可靠性。
- 为了减小短沟道效应的影响,需要在器件结构上进行改进,如采用轻掺杂漏极结构(LDD)、绝缘衬底上硅结构(SOI)、薄氧栅等。
窄沟道效应
- 当MOSFET的沟道宽度约等于源和漏结的耗尽层宽度时,即为所谓“窄沟道”器件。在器件结构的尺寸缩小时,不仅沟道长度变短,宽度也将按同比例在缩小,于是就会出现窄沟道器件。
- 窄沟道效应会导致MOSFET的阈值电压随着沟道宽度的变窄而增大。这是由于栅极的“边缘场”或者场区离子注入的侧向扩散影响了场氧化层下的表面耗尽区的空间电荷。
- 窄沟道效应和短沟道效应有时可以相互补偿,从而使得小尺寸器件的阈值电压与大尺寸器件的一样。为了减小窄沟道效应的影响,需要在器件结构或工艺上进行改进。
DIBL效应(漏致势垒降低效应)
- 当MOSFET的沟道长度很短时,漏PN结上的反偏会对源PN结发生影响,使漏、源之间的势垒高度降低,从而有电子从源PN结注入沟道区,使漏电流增大。这种由漏极导致的势垒下降现象称为DIBL效应。
- DIBL效应会导致MOSFET的阈值电压随着漏极电压的增加而下降,从而影响器件的性能和可靠性。例如增加亚阈特性、热载流子效应、热噪声等。
- 为了抑制DIBL效应,需要在器件结构或工艺上进行改进,例如采用轻掺杂漏极结构(LDD)、绝缘衬底上硅结构(SOI)、多栅极结构(FinFET)等。
亚表面穿通效应
MOSFET的亚表面穿通效应是指当MOSFET的沟道长度缩小到一定程度时,源极和漏极之间的耗尽区会相互接触,导致电子可以从源极直接穿透到漏极,而不受栅极电压的控制。这样,MOSFET就无法完全截止,会产生较大的亚阈值泄漏电流。亚表面穿通效应会降低MOSFET的开关性能和功耗效率,是一种不利的短沟道效应。
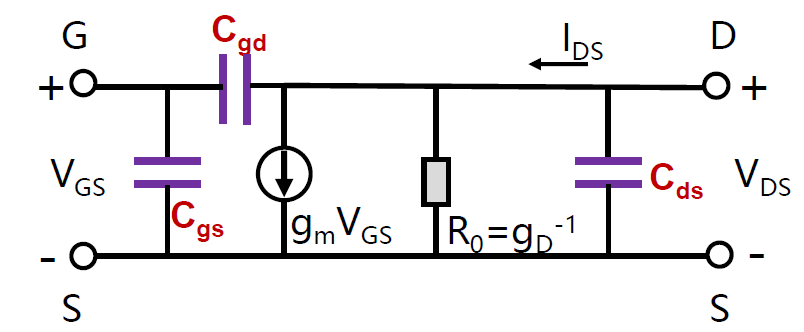
等效电路
低频
高频
计算题解题步骤
- 确定 $V_{GS}$、$V_{DS}$、$V_{T}$
- 如果 $V_{GS}-V_T<0$,则 MOSFET 处于截止状态,没有电流通过。
- 如果 $0<V_{GS}-V_T<V_{DS}$,则 MOSFET 处于非饱和区(线性区),电流与 $V_{DS}$ 成线性关系。
- 如果 $V_{GS}-V_T>V_{DS}$,则 MOSFET 处于饱和区,电流与 $V_{GS}$ 成平方关系。
- 跨导参数
- 跨导系数
- 跨导
非饱和区饱和区
BJT
优势
BJT相比MOSFET有以下几个优势
- BJT的开关速度更快,适合高频应用。
- BJT的驱动电压更低,只需0.7V左右,而MOSFET需要几伏的栅极电压。
- BJT的输出电阻更高,可以提供更大的跨导和增益。
- BJT的噪声更小,适合低信噪比的放大器。
- BJT的价格更便宜,种类更多,选择性更大。
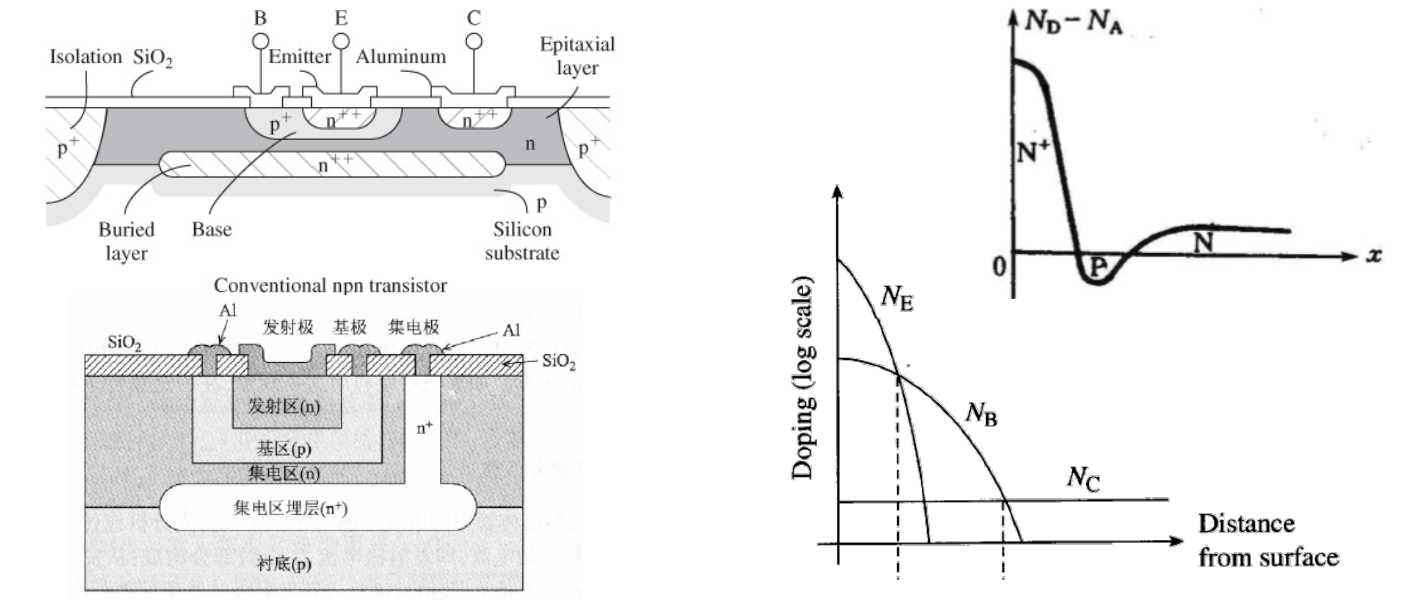
基本结构
双极晶体管基本结构:由三个掺杂不同的扩散区形成两个背对背pn结。三个区对应晶体管的三个电极:发射极、基极、集电极;相应称为发射结、集电结。根据三个电极掺杂类型不同分为两类:npn型和pnp型。
BJT在基区传输电流,依靠少子传输,故是少子器件
合金结晶体管
- 非对称的几何结构
- 掺杂浓度依次从发射极、基极、集电极降低
- 基极层做的很薄
- 基区无电场,电子容易湮灭
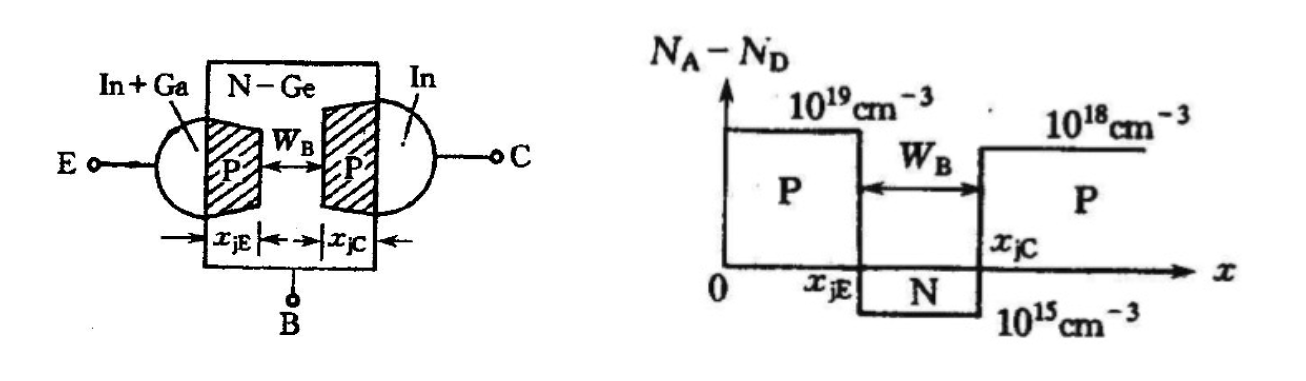
扩散结晶体管
- 非对称的几何结构
- 掺杂浓度依次从发射极、基极、集电极降低
- 基极层做的很薄
- 集电结面积往往远大于发射结面积
- 基区有电场,电子可以漂移
三种接法
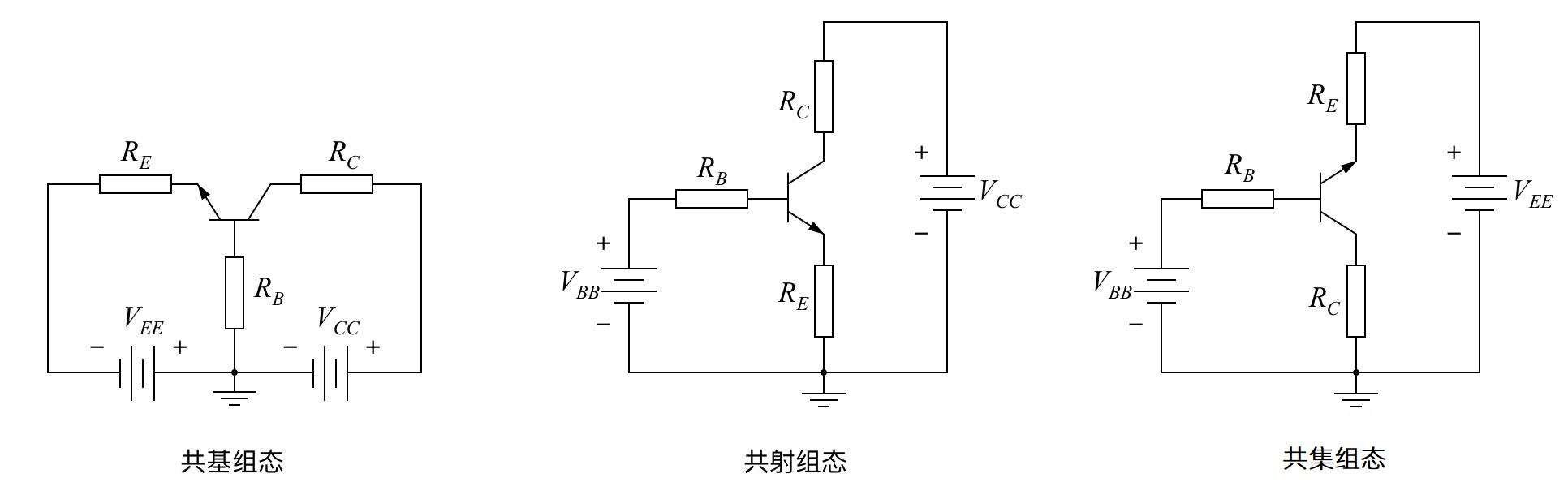
- 共射电路既能放大电流又能放大电压,输入电阻居三种电路之中,输出电阻较大,频带较窄。常作为低频电压放大电路的单元电路。
- 共集电路只能放大电流不能放大电压,是三种接法中输入电阻最大,输出电阻最小的电路,并具有电压跟随的特点。常用于电压放大电路的输入级和输出级,在功率放大电路中也常采用射极输出的形式。
- 共基电路只能放大电压不能放大电流,具有电流跟随的特点;输入电阻小,电压放大倍数、输出电阻与共射电路相当,是三种接法中高频特性最好的电路。常作为宽频带放大电路。
| $A_\mathrm{v}$ | $A_\mathrm{i}$ | $R_\mathrm{i}$ | $R_\mathrm{o}$ | 频带 | |
|---|---|---|---|---|---|
| 共射 | 大 | $\beta$ | 中 | 大 | 窄 |
| 共集 | 小于 1 | $1+\beta$ | 大 | 小 | 中 |
| 共基 | 大 | $\alpha$ | 小 | 大 | 宽 |
能带图&工作原理
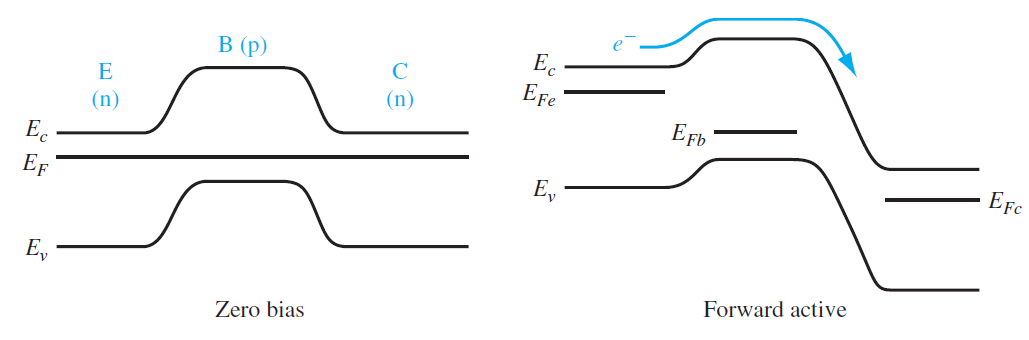
BJT工作基础:非平衡少子的扩散运动
需要满足的三个工作条件:
- $W_b \ll L_{nb}$
- 发射结正偏
- 集电结反偏
晶体管放大原理
- 发射结正偏:N+区大量电子注入到基区(P区)
- 基区宽度远小于电子的扩散长度:则注入电子除少部分被复合外,绝大部分会扩散到集电结耗尽区边界处
- 集电结反偏:较宽的空间电荷区内有很强电场,因而扩散到集电结边缘的电子会立即被强电场扫入集电区,形成集电区电流
- 注入电子电流(源于正偏发射结),远大于集电结的反向饱和电流(集电结反偏),构成集电极电流的主要部分
参数
- 共基极电流放大系数其中:
- 发射效率(注入比)
- 基区传输系数
集电区倍增因子 $\alpha^{*}$
共发射极电流放大系数
电流传输情况
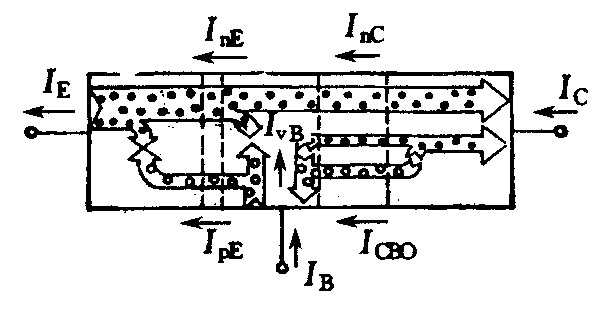
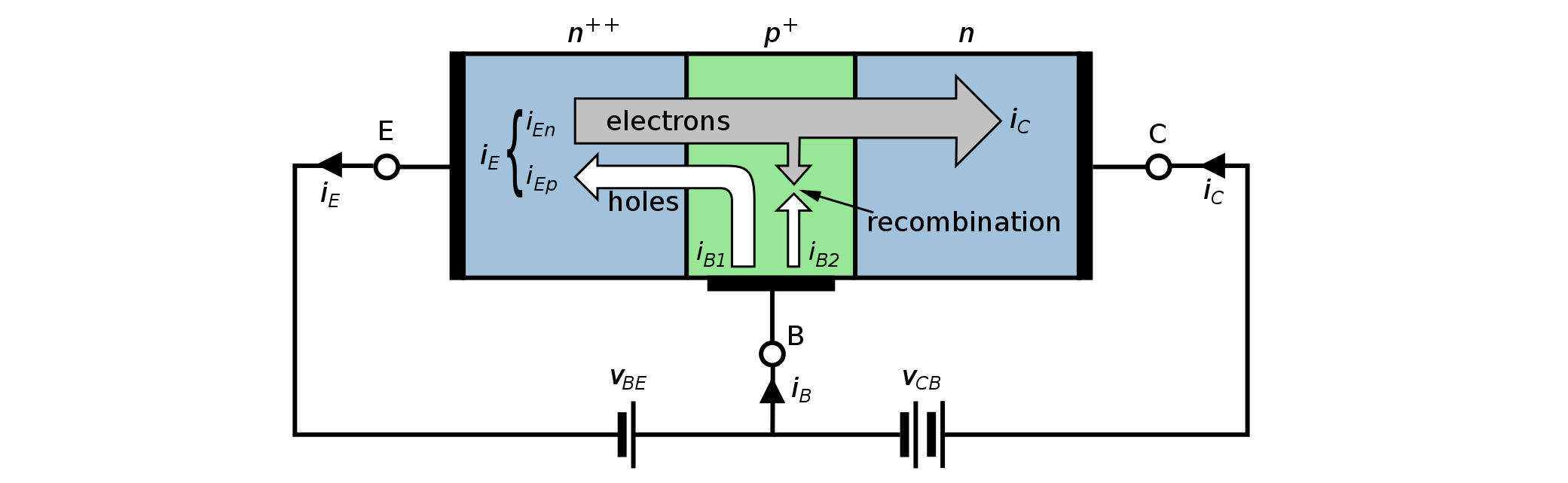
内部:
外部:
少子浓度
特殊点分布
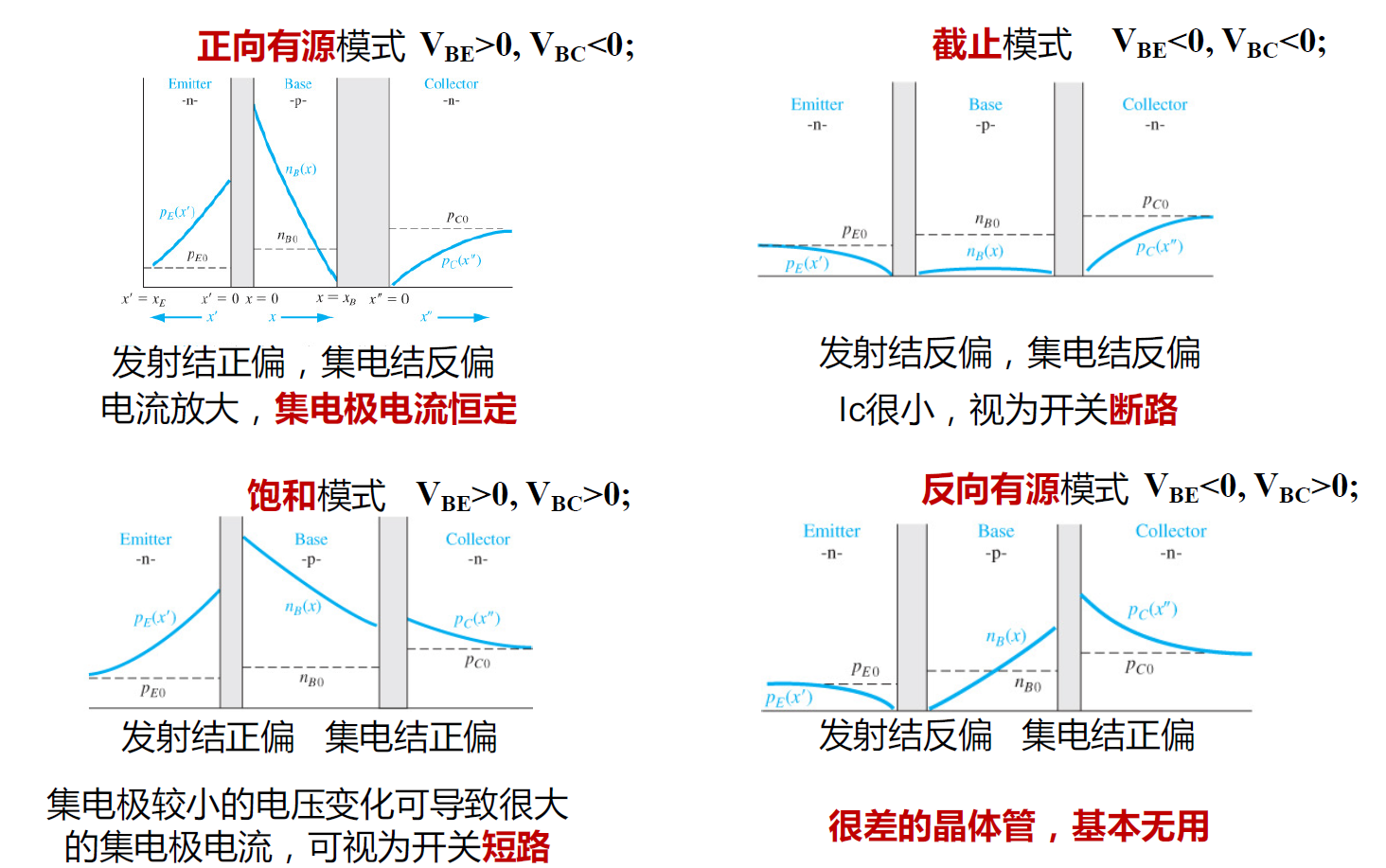
发射结正偏(VBE>0),发射结反偏(VBC<0)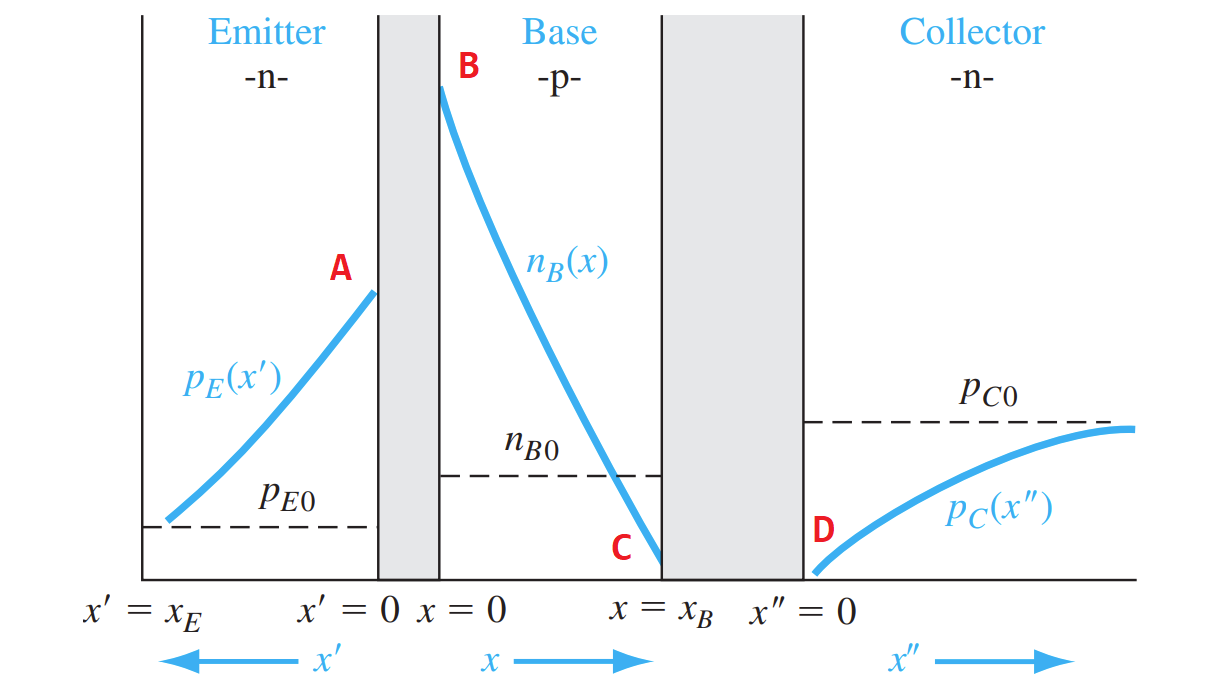
A点:
由PN结定律
n是多子,$n=(x’=0)=N_{D}$,故
BCD点:同理
基区分布
由少子扩散方程,简化得
边界条件
解得
考虑到基区宽度 $x_B$ 比少子扩散长度 $L_B$ 小很多,则有近似
线性衰减,物理含义:就是不考虑复合。
发射区分布
边界条件
解得
集电区分布
边界条件
解得
电流密度的计算
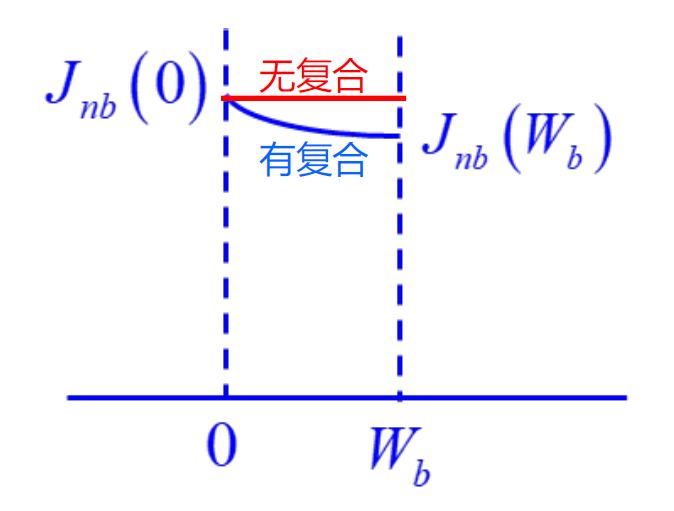
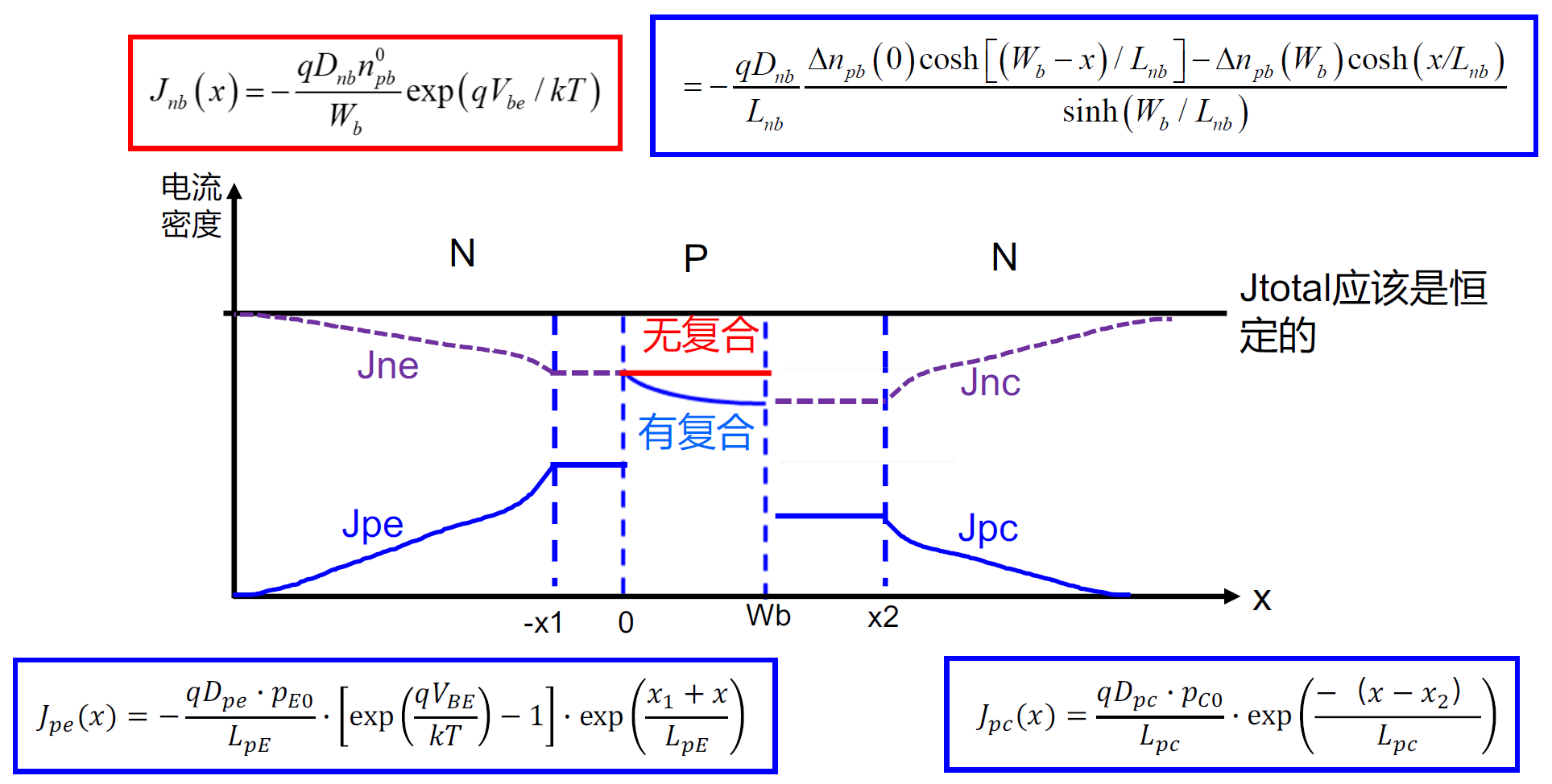
理想BJT的电流-电压方程
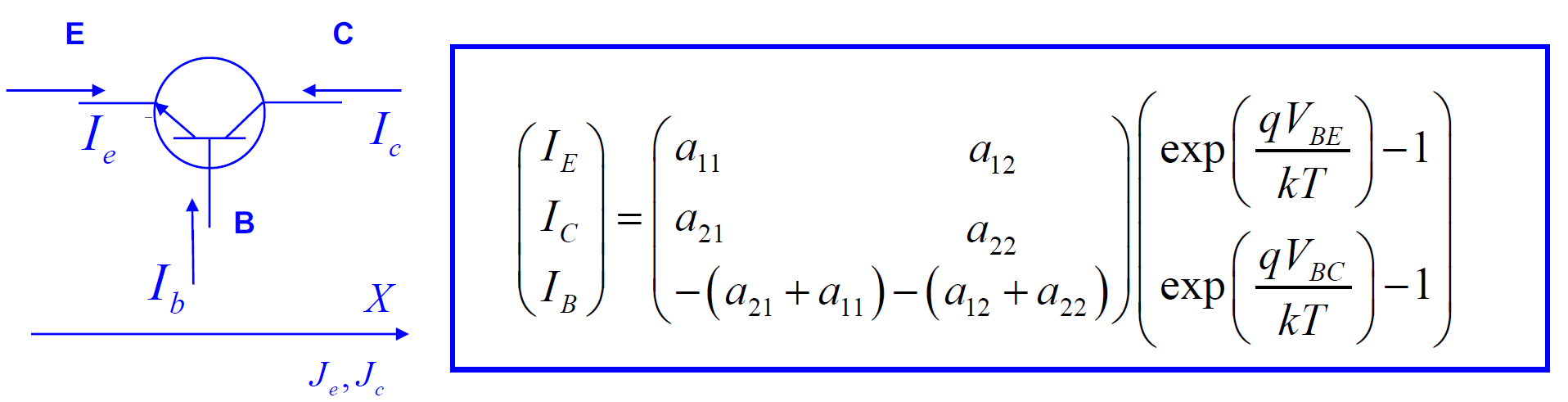
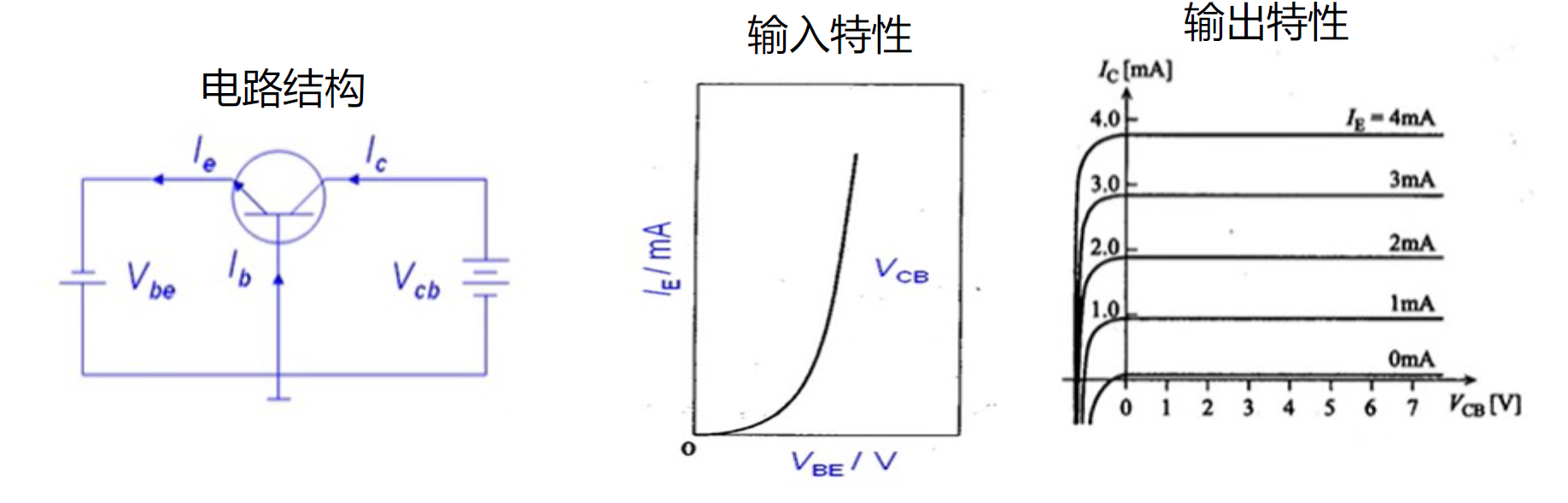
输入输出特性
共基极
共射极
四种工作模式下的少子分布
非理想特性
结面积导致的非理想效应
发射区载流子向非本征基区流动,损失较多
厄利效应(基区宽度调制效应)
基宽调制是由于集电结的反向偏压会影响基区的有效宽度,当集电结的反向偏压增加时,基区的有效宽度减小,导致发射结注入的少子在基区中复合的概率减小,从而增加了集电极电流。基宽调制会影响BJT的输出特性和放大系数,因为它使得集电极电流不仅与发射结正向偏压有关,还与集电结反向偏压有关。基宽调制与基区面积成反比,因此基区面积越小,基宽调制越明显。
复合效应
发射结复合电流是指 发射区扩散到基区的电子与基区的空穴复合而产生的电流。它是基极电流的一部分,也是发射极电流的损失。发射结复合电流与发射区和基区的掺杂浓度、发射结正向偏压、基区宽度等因素有关。发射结复合电流越小,BJT的电流放大系数越高。
Kirk效应(基区展宽效应)
在大电流工作时,集电结反向偏置的耗尽层向基区侵入,使得有效的基区宽度减小的一种现象。(大量注入的电子进入集电结,集电结空间电荷区展宽,α和β都变小)
这种效应会导致BJT的电流增益下降和早饱和现象,影响BJT的高频功率性能。
抑制Kirk效应的措施主要是限制集电极电流密度,提高集电区的掺杂浓度,减小集电区的厚度等。
集边效应(基极电阻自偏压效应)
发射极电流集边效应,是指 BJT 在大电流工作时,发射极电流集中到发射结的周围边缘(周围是无效的,中间才有效),减小了发射结的有效面积。这种效应是由于基极电阻所引起的,它会影响 BJT 的发射极注射效率、电流放大系数、频率特性 等性能。限制或者削弱发射极电流集边效应的措施有限制电流容量、提高基区掺杂浓度、提高发射极周长/面积比等方法。
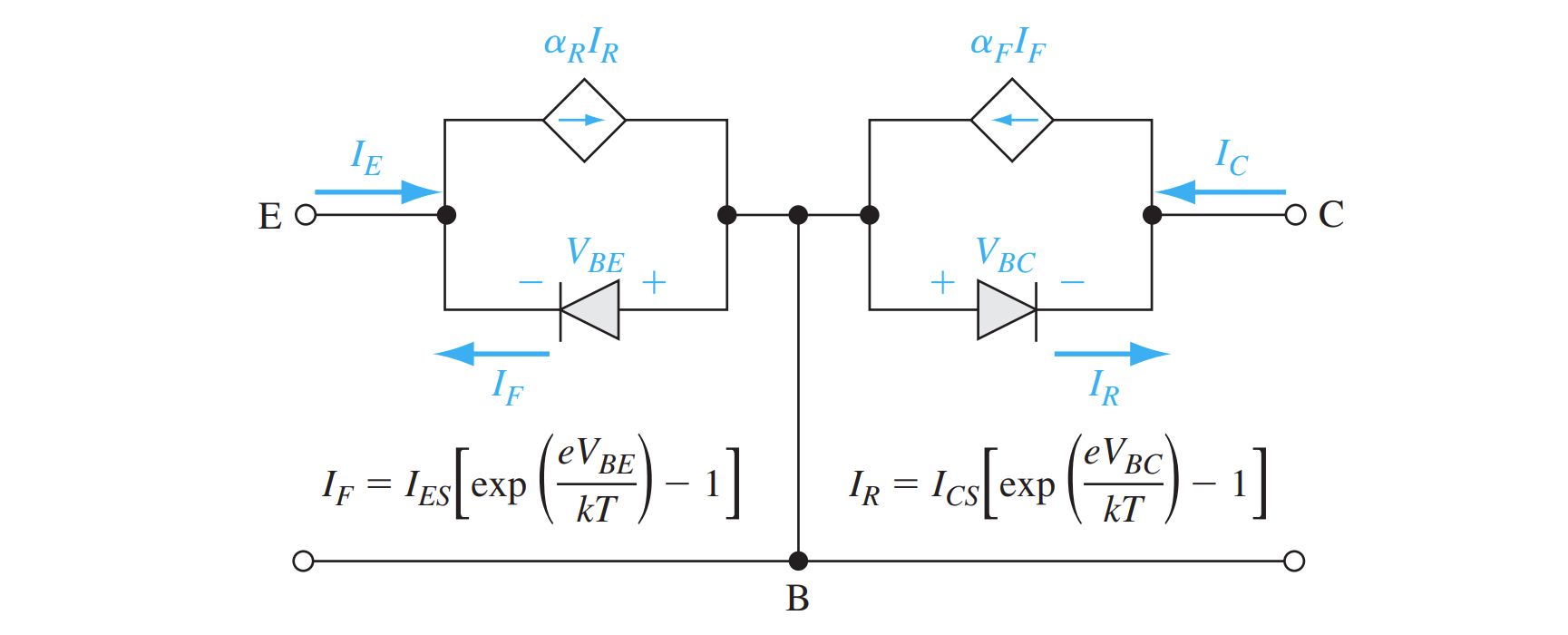
Ebers-Moll 模型
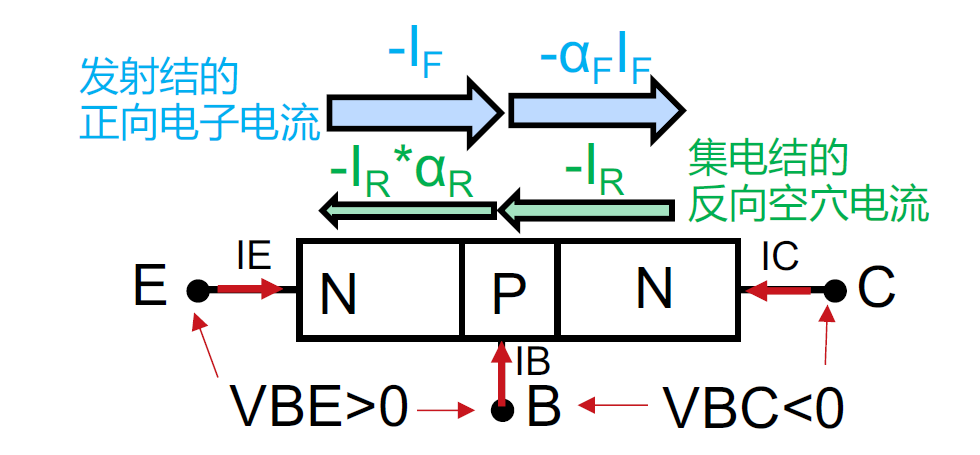
发射结的正向电子电流 $I_F$,集电结的反向空穴电流 $I_R$
其中
- $\alpha_{F}$:正向有源状态下的共基级电流增益
- $\alpha_{R}$:反向有源状态下的共基级电流增益
- $\alpha_{F}I_{F0}=\alpha_{R}I_{R0}$
存储器
分类
按速度分: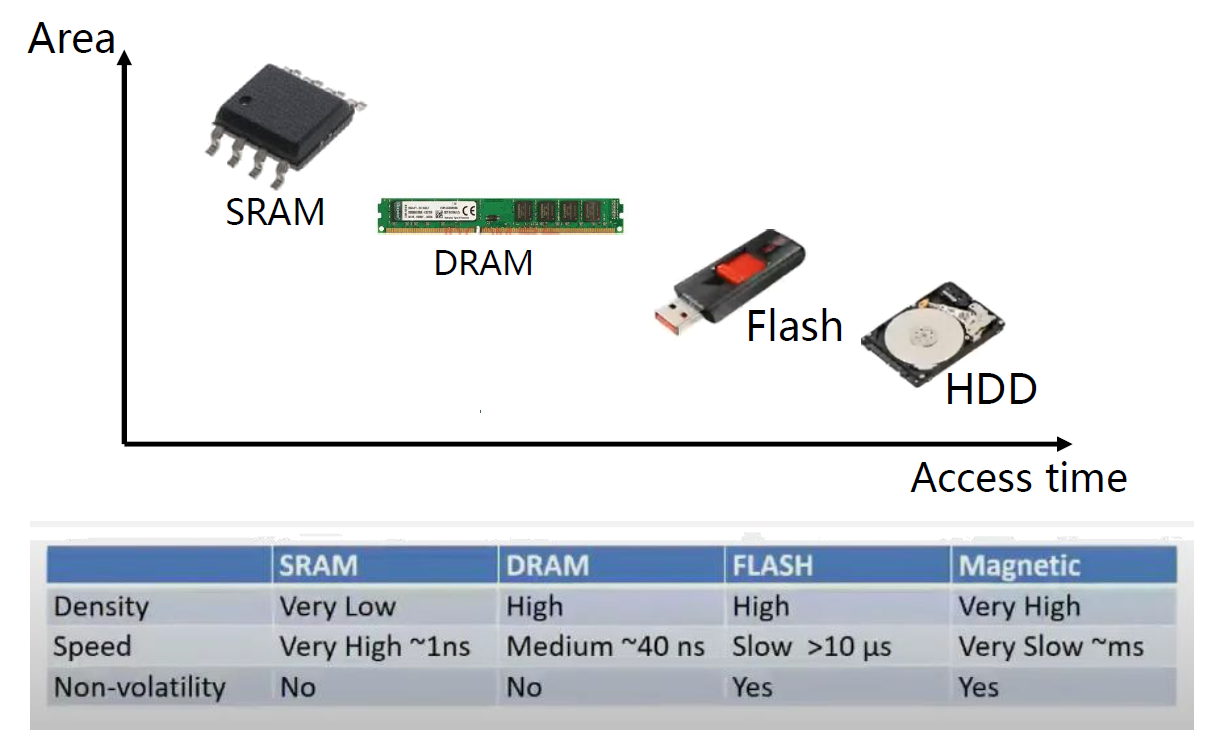
按易失性分: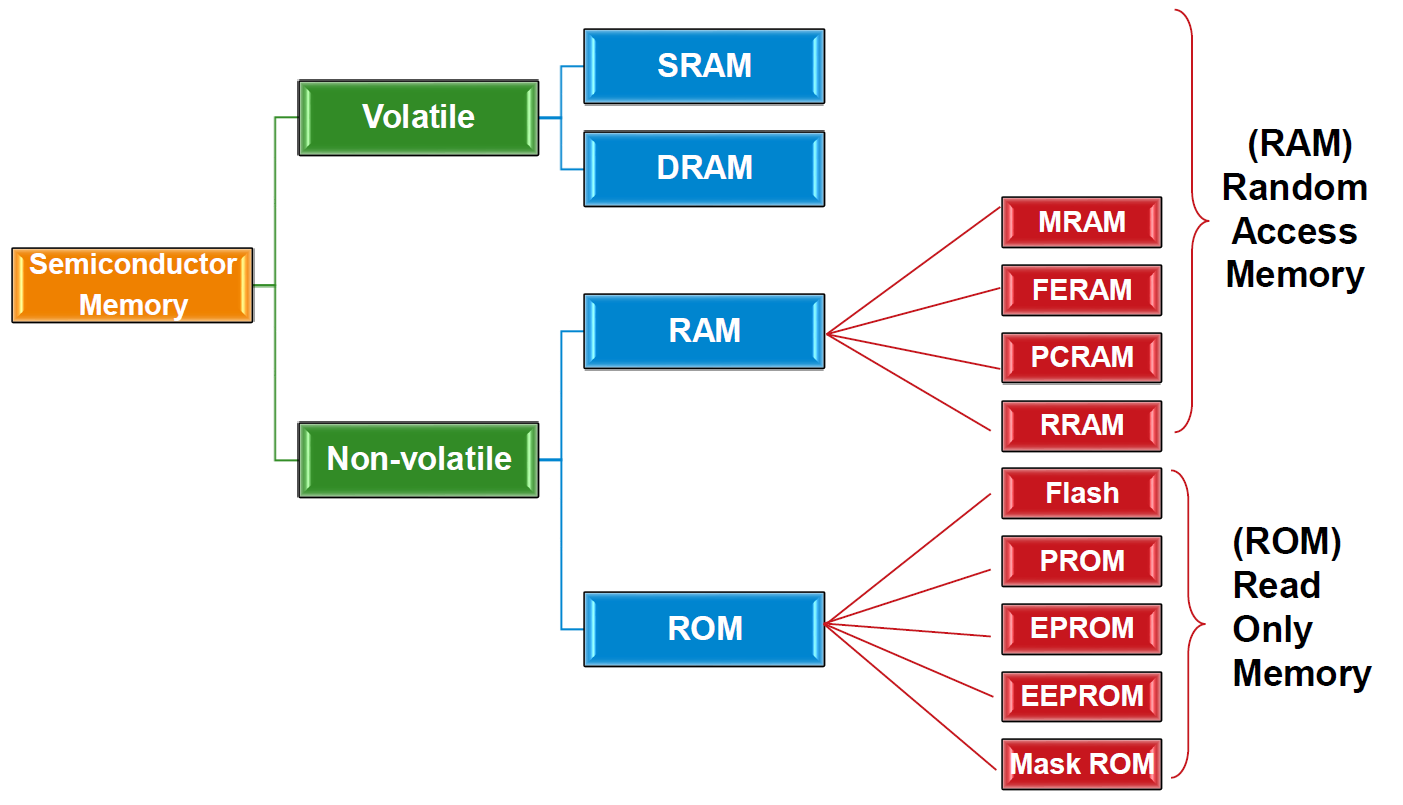
SRAM
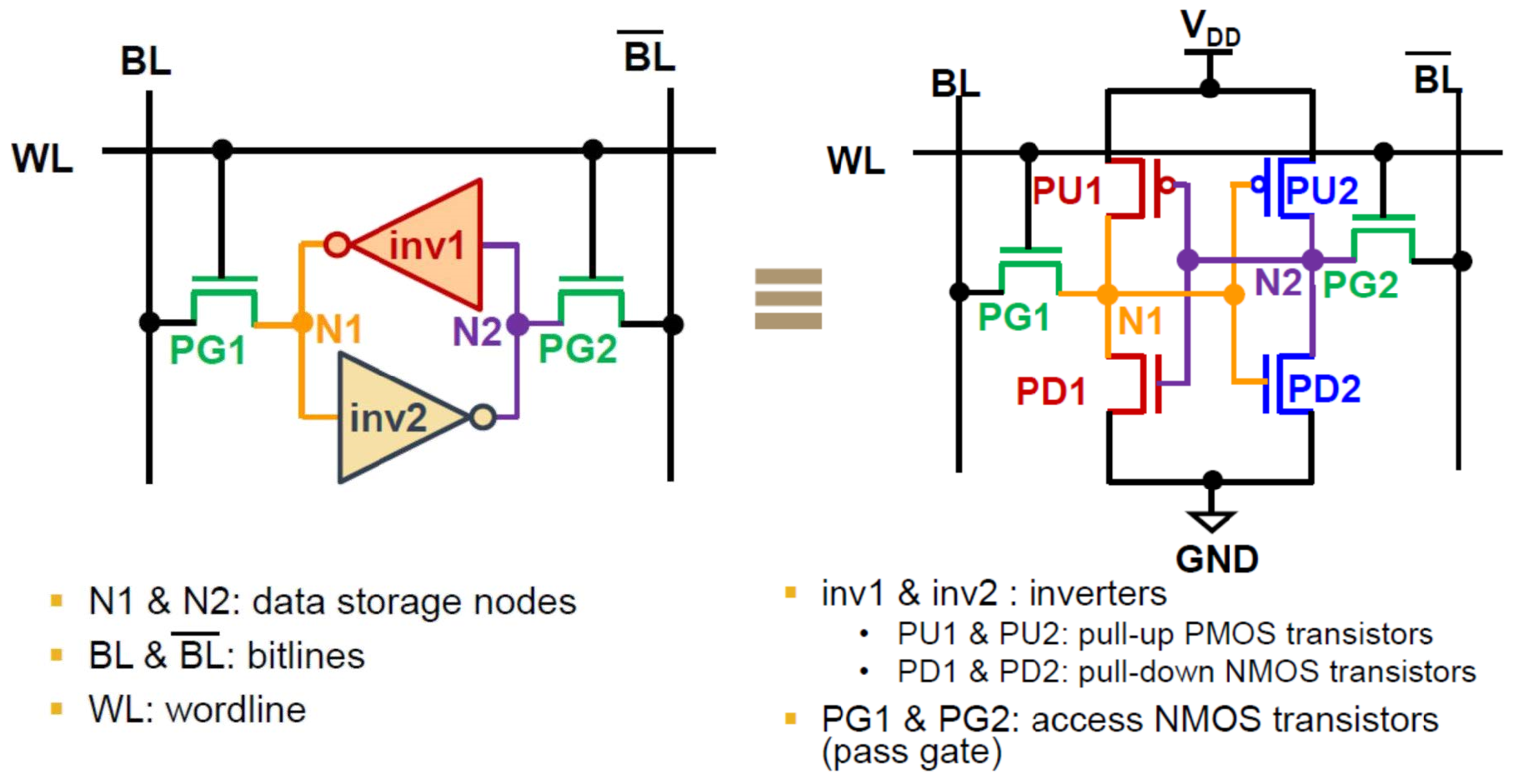
- 读操作:首先对 $BL$ 和 $\overline{BL}$ 进行预充电,使它们都为高电平。然后根据要读取的地址,选通对应的 $WL$,使其为高电平。这样,选中的存储单元就与 $BL$ 和 $\overline{BL}$ 连通,根据其存储的数据,会使 $BL$ 和 $\overline{BL}$ 中的一个下降电压(0),另一个保持不变(1)。这样就形成了一个电压差,通过外围放大电路输出,就可以读取到存储单元中的数据。
- 写操作:首先根据要写入的数据,对 $BL$ 和 $\overline{BL}$ 进行设置,使它们互为反相(0和1)。然后根据要写入的地址,选通对应的 $WL$,使其为高电平(1)。这样,选中的存储单元就与 $BL$ 和 $\overline{BL}$ 连通,根据 $BL$ 和 $\overline{BL}$ 的电压差,会使存储单元中的数据反转(0变1或1变0)。这样就完成了写入操作。
- 保持操作:当不进行读写操作时,对 $BL$ 和 $\overline{BL}$ 保持高电平(1),对 $WL$ 保持低电平(0)。这样,所有的存储单元都与 $BL$ 和 $\overline{BL}$ 断开,保持原来的数据不变。
DRAM
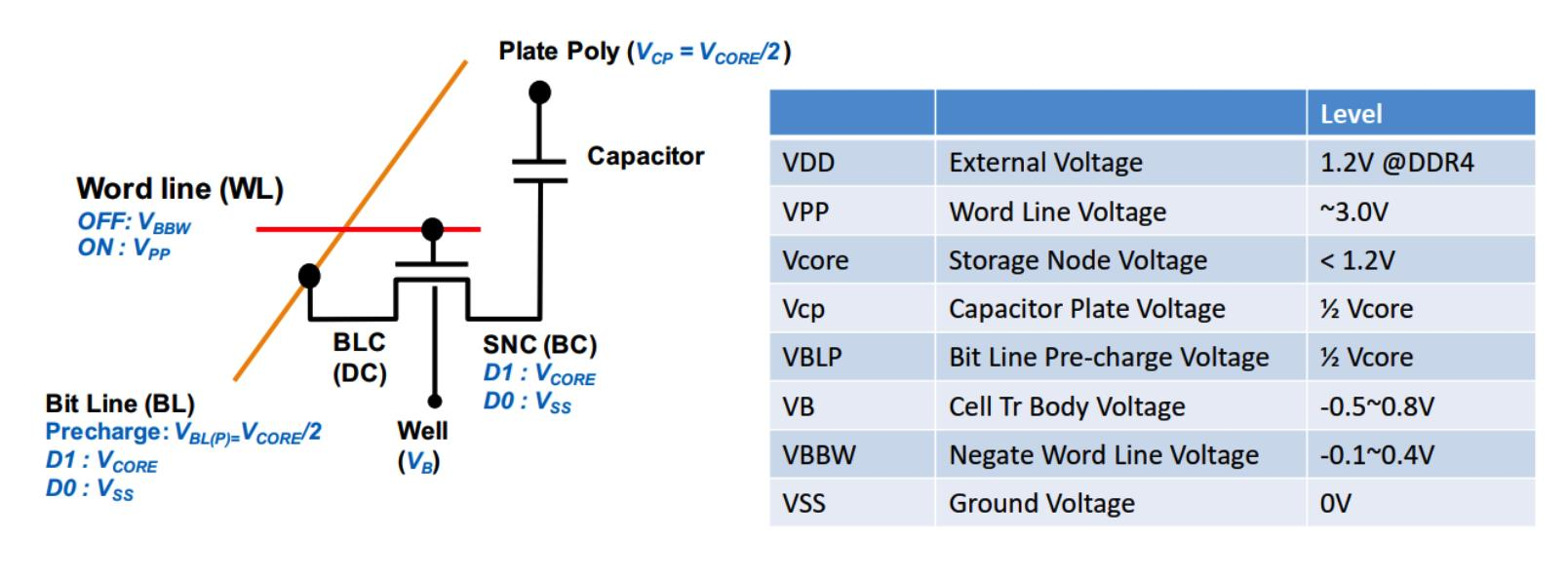
- 读操作:首先对 $BL$ 进行预充电,使它为中间电平(VDD/2)。然后根据要读取的地址,选通对应的 $WL$,使其为高电平(VDD)。这样,选中的存储单元就与 $BL$ 连通,根据其存储的数据(电容上的电荷),会使 $BL$ 的电压上升或下降一定幅度。这样就形成了一个小信号,通过外围放大电路输出,就可以读取到存储单元中的数据。由于读取过程会破坏电容上的电荷,所以需要在读取后对电容进行恢复充电。
- 写操作:首先根据要写入的数据,对 $BL$ 进行设置,使它为高电平(VDD)或低电平(0)。然后根据要写入的地址,选通对应的 $WL$,使其为高电平(VDD)。这样,选中的存储单元就与 $BL$ 连通,根据 $BL$ 的电压差,会使存储单元中的数据反转(0变1或1变0)。这样就完成了写入操作。
- 保持操作:当不进行读写操作时,对 $WL$ 保持低电平(0),对 $BL$ 保持高阻态。这样,所有的存储单元都与 $BL$ 断开,保持原来的数据不变。但是由于电容会有漏电流,导致电荷逐渐衰减,所以需要定期对所有的存储单元进行刷新操作,即重新读取并恢复每个存储单元中的数据。
FLASH
FLASH存储的原理是利用浮栅场效应管(Floating Gate MOSFET)来存储电荷,从而表示二进制数据。FLASH存储器有两种主要类型:NOR Flash和NAND Flash。
NOR Flash的结构类似于NOR门,每个存储单元都直接连接到地址线和数据线,可以实现随机访问和执行就地(XIP)。NOR Flash的容量较小,读取速度较快,但是写入和擦除速度较慢,成本较高,一般用于存储程序代码。
NAND Flash的结构类似于NAND门,每个存储单元都串联在一起形成一个字符串,然后通过选通晶体管连接到位线(bitline)。NAND Flash不能实现随机访问和执行就地(XIP),只能按页(page)或块(block)进行读写和擦除操作。NAND Flash的容量较大,写入和擦除速度较快,但是读取速度较慢,成本较低,一般用于存储大容量的数据。
FLASH存储器的读写和擦除操作都是通过控制栅极(control gate)和衬底(substrate)之间的电压差来实现的。
- 读操作:根据要读取的地址,选通对应的控制栅极,使其为高电平或低电平,然后测量位线上的电流或电压变化,判断浮栅中是否有电荷,从而读取出数据。
- 写操作:根据要写入的数据,对位线进行设置,使其为高电平或低电平,然后对选中的控制栅极施加高电压,使得电子通过热电子注入或Fowler-Nordheim隧穿效应进入浮栅中,从而改变浮栅中的电荷状态。
- 擦除操作:对选中的控制栅极施加低电压或接地,然后对衬底施加高电压,使得浮栅中的电子通过Fowler-Nordheim隧穿效应离开浮栅中,从而恢复浮栅中的电荷状态。
FLASH存储器的优点是非易失性、低功耗、高密度、可重复擦写等;缺点是有限的擦写次数、需要刷新操作、存在坏块问题等。
先进晶体管
应变工程
- 源漏嵌入SiC应变技术:通过在NMOS的源漏区域外延生长SiC应变材料,利用硅和碳的晶格常数不同,对沟道和衬底硅产生拉应力,改变硅导带的能带结构,降低电子的电导有效质量和散射概率,从而提高NMOS的速度。
- 源漏嵌入SiGe应变技术:通过在PMOS的源漏区域外延生长SiGe应变材料,利用锗和硅的晶格常数不同,对沟道和衬底硅产生压应力,改变硅价带的能带结构,降低空穴的电导有效质量,从而提高PMOS的速度。
HKMG
Why
随着工艺的演进,tox 越来越小,导致栅氧化层漏电越来越严重。高 K 金属栅的引入,可以明显提高氧化层的物理厚度,抑制漏电。
How
在早期的时候,栅极采用的是铝金属栅极。采用的相关配套的结构是铝金属/纯二氧化硅;后来经过发展采用了多晶硅栅,采用的结构仍然是多晶硅栅/纯二氧化硅;后来又经过一段发展,便成为了多晶硅栅/SiON;然后在进入45nm以后技术节点的时候采用了HKMG。
原来是用铪基材料代替了SiON,但是铪基材料与多晶硅栅的兼容性一直是一个问题,所以需要采用金属栅。
高K介质的选择:
- 需要与 Si 衬底形成稳定的界面
- 热稳定性好,形成非晶
- 需要与 Si 衬底形成较大的带边偏移量,减少漏电
- HfO2 和 La2O3 是比较理想的高 K 介质
金属栅极的选择主要因素包括:
- 金属栅极的功函数
- 较高的热稳定性
- 较低的界面态密度
- HKMG整合工艺
- 金属栅有效功函数的调制
- 金属栅极的制备方法
FinFET
器件的漏电路径发生在远离沟道的地方,
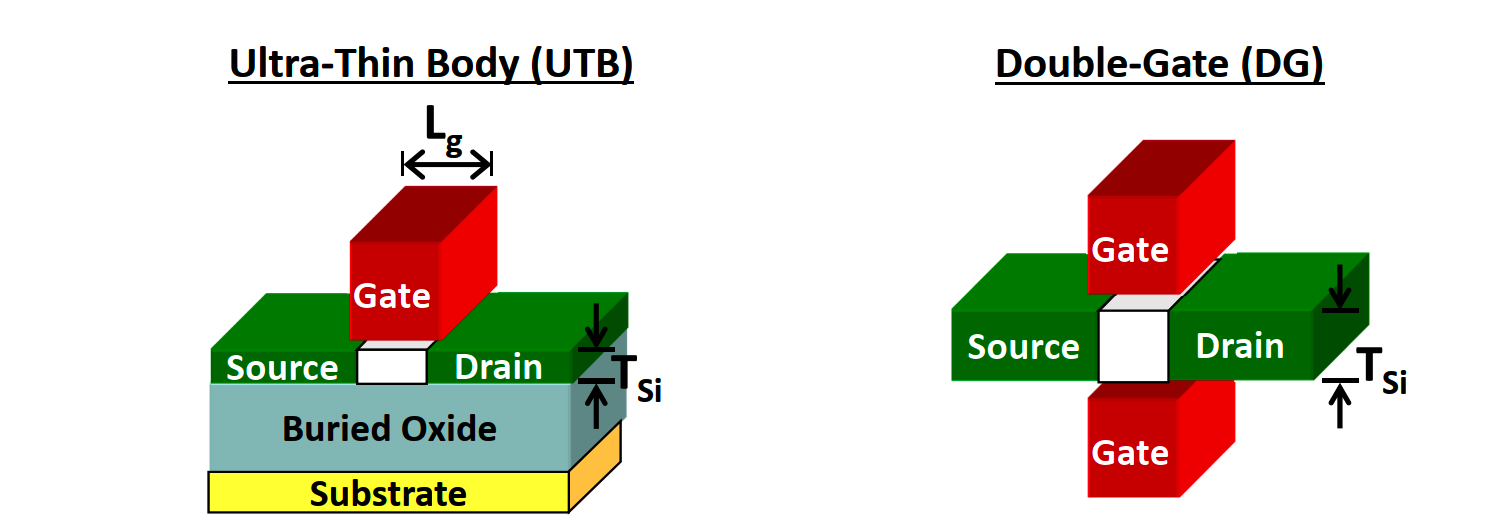
- 采用 UTB 结构或者双栅结构,可以阻断电流泄漏路径
- 采用薄硅衬底,可以显著抑制漏电
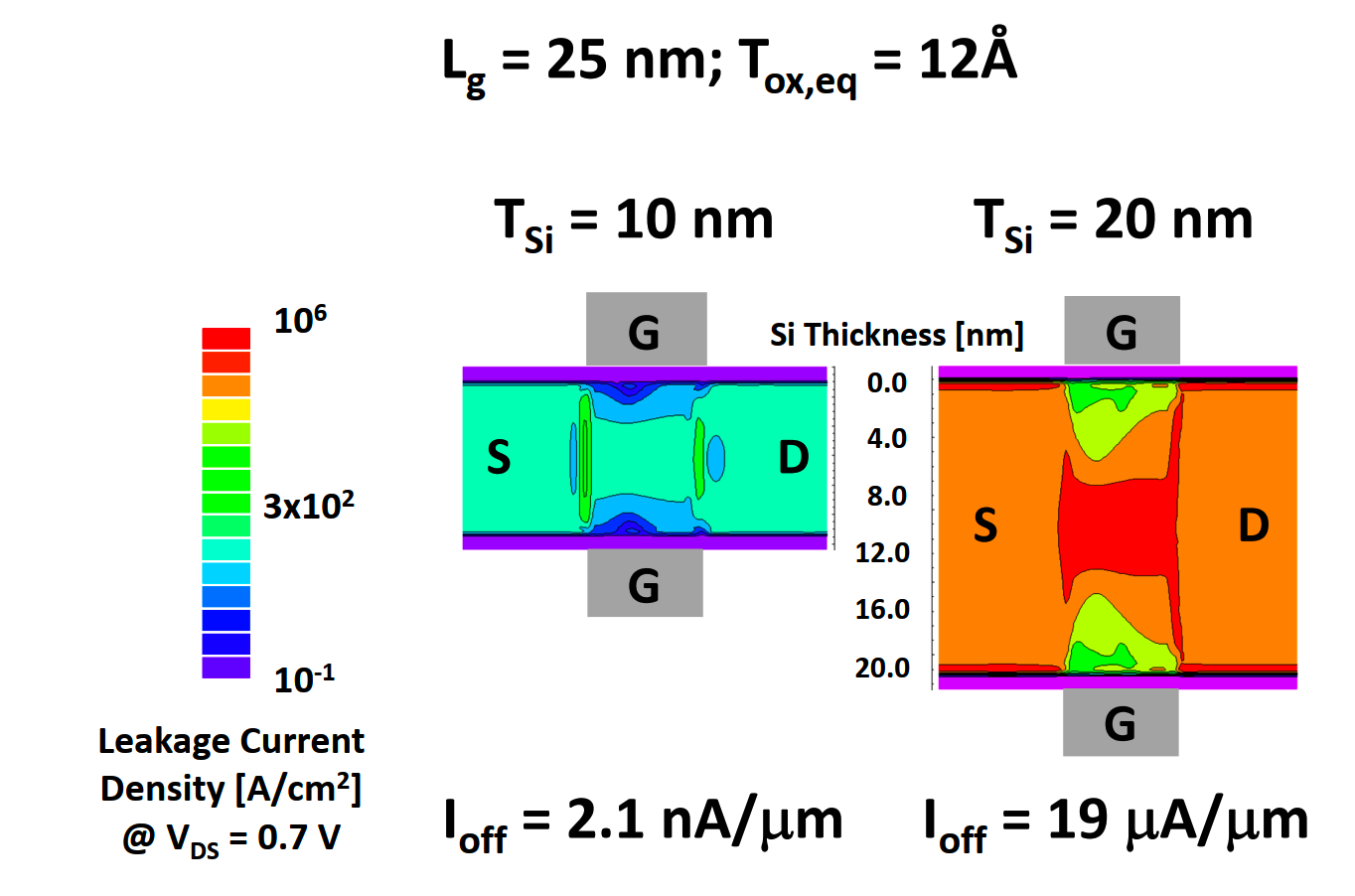
FinFET 器件的 SS 理论上可以达到极限 60mV/dec
本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 协议 ,转载请注明出处!