数字集成电路设计笔记
本文最后更新于:2024年9月23日 上午
置顶
单位
| Letter | Unit | Magnitude |
|---|---|---|
| a | atto | $10^{-18}$ |
| f | fempto | $10^{-15}$ |
| p | pico | $10^{-12}$ |
| n | nano | $10^{-9}$ |
| u | micro | $10^{-6}$ |
| m | mili | $10^{-3}$ |
| k | kilo | $10^{3}$ |
| x | mega | $10^{6}$ |
| g | giga | $10^{9}$ |
第一章 引论
电压传输特性
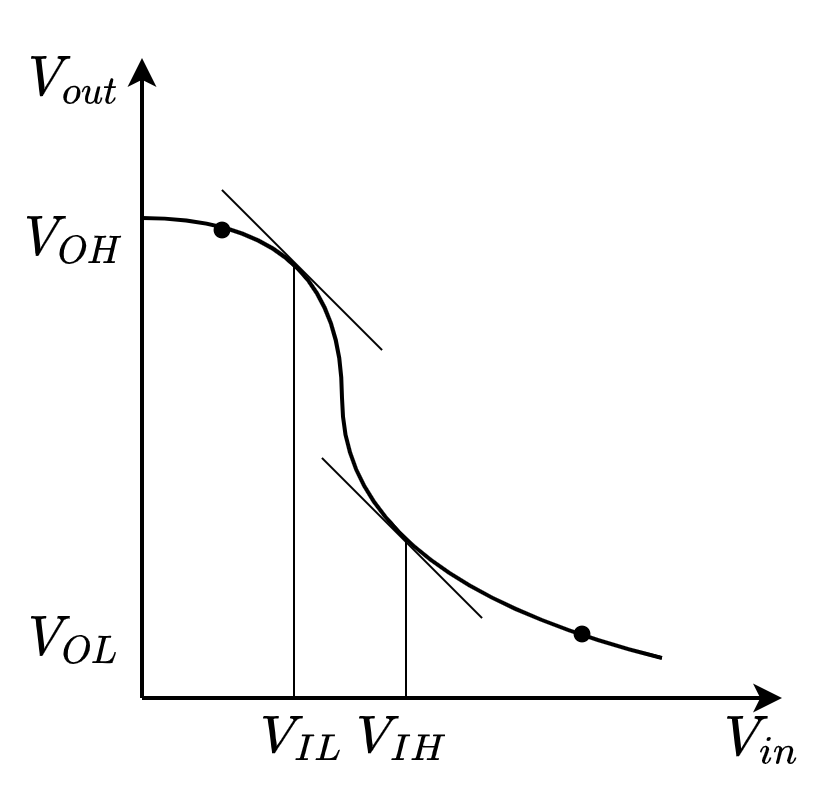
现在假设一个反相门电路的输入为逻辑变量 in,它产生输出变量 out。一个逻辑门的电路功能可以用它的电压传输特性(VTC,有时称为 DC 传输特性)得到最佳描述,它画出了输出电压与输入电压的关系 $V_{out}=f\left(V_{in}\right)$
- 额定高电压 $V_{OH}$ 和额定低电压 $V_{OL}$
- 门阈值电压或开关阈值电压 $V_{M}$
- VTC 增益
- 可接受的高电压 $V_{IH}$ 和低电压 $V_{IL}$ 代表了 VTC 增益等于 -1 的点
噪声容限
一个门对噪声的灵敏度是由低电平噪声容限 $N M_{L}$ 和高电平噪声容限 $N M_{H}$ 来度量的。它们分别量化了合法的“0”和“1”的范围,并确定了噪声的最大固定阈值:
再生性
再生性保证一个受干扰的信号在通过若干逻辑级后逐渐收敛回到额定电平中的一个。
抗噪声能力
其中 $V_{N f_{i}}$ 是外界系统电压,$V_{SW}$ 是电源电压
扇入和扇出
- 扇出表示连接到驱动门输出端的负载门的数目 N。
- 增加一个门的扇出会影响它的逻辑输出电平。通过使负载门的输入电阻尽可能地大(也就是使输入电流最小)并保持驱动门的输出电阻较小(即减小负载电流对输出电压的影响),可以使这一影响减到最小。
- 当扇出较大时,所加的负载会使驱动门的动态性能变差。为此许多通用单元和库单元都定义了一个最大扇出数来保证该单元的静态和动态性能都能满足规定的技术要求。
- 扇入定义为该门输入的数目。扇入较大的门往往比较复杂,这常常会使静态和动态特性变差。
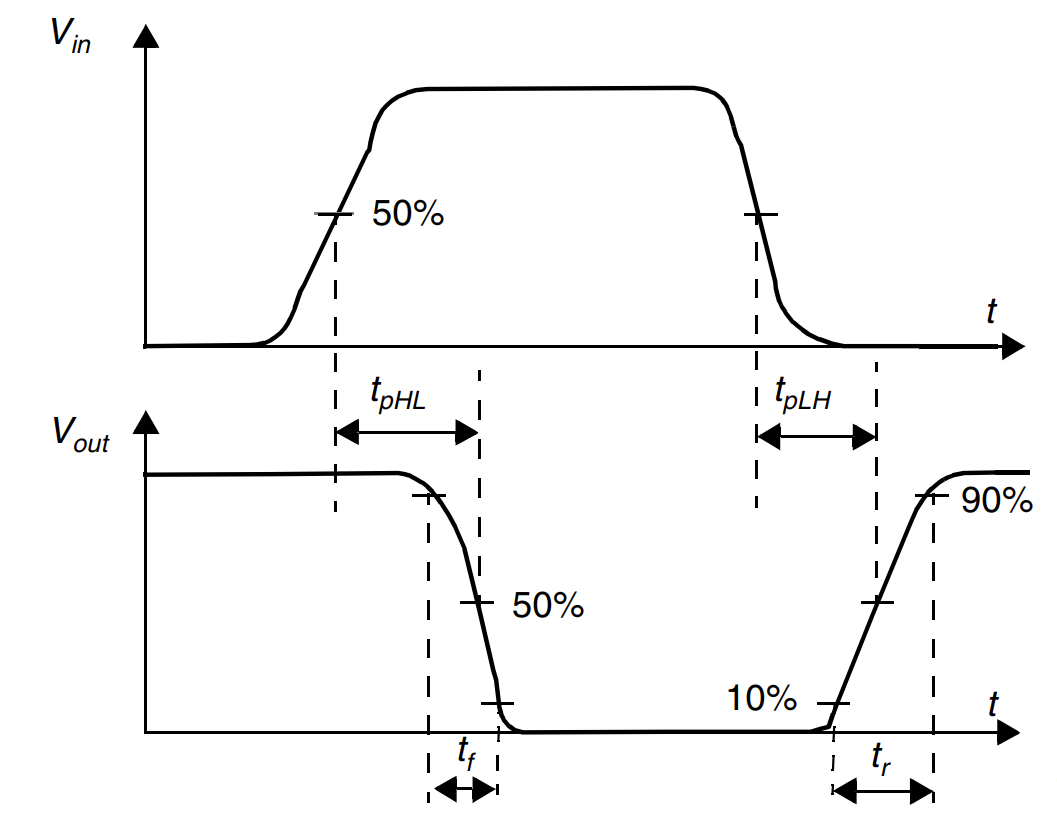
传播延时
一个门的传播延时 $t_{p}$ 定义了它对输入端信号变化的响应有多快。它表示一个信号通过一个门时所经历的延时,定义为输入和输出波形的 $50\%$ 翻转点之间的时间。由于一个门对上升和下降输入波形的响应时间不同,所以需要定义两个传播延时。$t_{p L H}$ 定义为这个门的输出由低至高(或正向)翻转的响应时问,而 $t_{p H L}$ 则为输出由高至低(或负向)翻转的响应时间。传播延时 $t_{p}$ 定义为这两个时间的平均值:
- 传播延时(Propagation delay time)$t_{pd}=\max\{t_{p L H},t_{p H L}\}$
- 污染延时(Contamination delay time)$t_{cd}=\min\{t_{p L H},t_{p H L}\}$
- 下降时间 $t_{f}$ 是从 90% 到 10% 所用的时间
- 下降时间 $t_{r}$ 是从 10% 到 90% 所用的时间
对于 RC 电路
- 充电:$V_{out}(t)=V_{dd}(1-e^{-t/\tau})$
- 放电:$V_{out}(t)=V_{dd}e^{-t/\tau}$
功耗与能耗
- 功耗可以进一步划分成静态部分和动态部分。
- 动态功耗只发生在门开关的瞬间。这是由于对电容充电以及在电源和地之间有一暂时的电流通路造成的,因此它正比于开关频率
- 静态功耗即使在没有发生开关时也存在,并且是由在电源和地之间的静态导电通路或由于漏电流引起的
- 一个门的传播延时和功耗有关,能量的传送越快(或者说功耗越大)则门越快。
- 对于给定的工艺和门的拓扑结构,功耗和延时的乘积一般为一常数。这一乘积称为功耗-延时积(PDP),它可以作为一个开关器件质量的度量。
- 一个理想的门应当快速且几乎不消耗能量,能量-延时积(E-D)是把这两个因素放在一起考虑的复合标准,它经常作为最后的质量评价。
晶圆
第二章 制造工艺
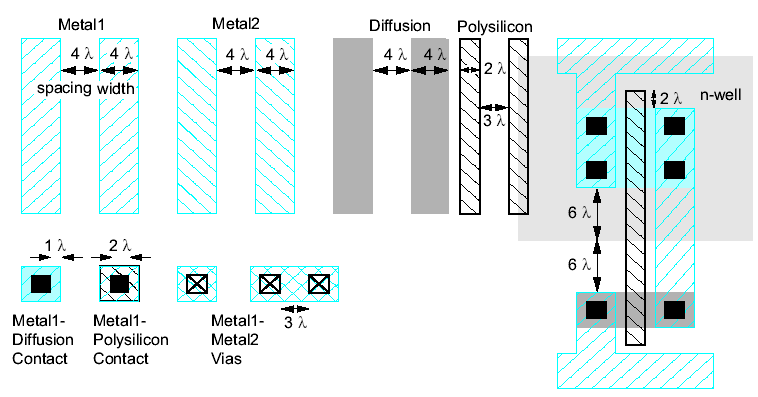
- Metal/diffusion have min. width 4λ
- Contacts are 2λ*2λ and be surrounded by 1λ
- Polysilicon uses a width of 2λ
- Polysilicon overlaps diffusion by 2λ and has a spacing of 2λ away
- Polysilicon and contacts have a spacing of 3λ from other poly or contacts
- N-well surrounds pMOS transistors by 6λ and avoids nMOS transistors by 6λ
- CONNECT is[metal-diffusion or metal-poly]
- VIA is metal-metal
第三章 器件
MOSFET 电容模型
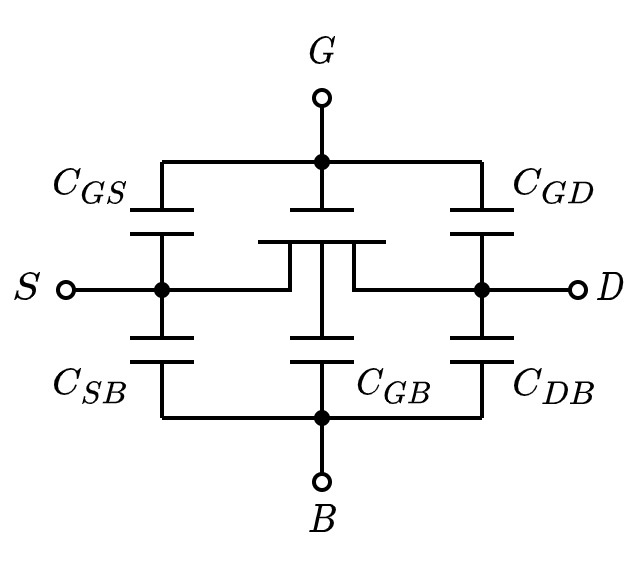
- 覆盖电容 $C_{overlap}=C_{GSO}+C_{GDO}$
- 栅至沟道的电容 $C_{GC}=C_{GCB}+C_{GCS}+C_{GCD}$
扩散电容 $C_{diff}=C_{Sdiff}+C_{Ddiff}$
$C_{GS}=C_{GSO}+C_{GCS}$
- $C_{GD}=C_{GDO}+C_{GCD}$
- $C_{GB}=C_{GCB}$
- $C_{SB}=C_{Sdiff}$
$C_{DB}=C_{Ddiff}$
$C_{G}=C_{GC}+C_{overlap}$
术语介绍
| 英文名 | 中文名 | 解释 |
|---|---|---|
| Overlap cap | 覆盖电容 | 源和漏在氧化层下延展的横向扩散引起的栅和源漏间的寄生电容 |
| Channel capacitances | 沟道电容 | 栅至沟道的电容,包含栅至源、栅至漏、栅至体的电容,是MOS最重要的寄生电路部分 |
| Junction/diffusion capacitances | 结电容/扩散电容 | 反向偏置的源体、漏体间的pn结引起的电容 |
| Bottom-plate cap | 底板电容 | 扩散区底板的pn结电容,由源/漏(掺杂为 $N_{D}$)和衬底(掺杂为 $N_{A}$)形成 |
| Side-well cap | 侧壁电容 | 扩散区侧壁的pn结电容,由源/漏(掺杂为 $N_{D}$)和掺杂为浓度为$N_{A}^{+}$ 的 $p+$ 沟道阻挡层注入形成 |
覆盖电容
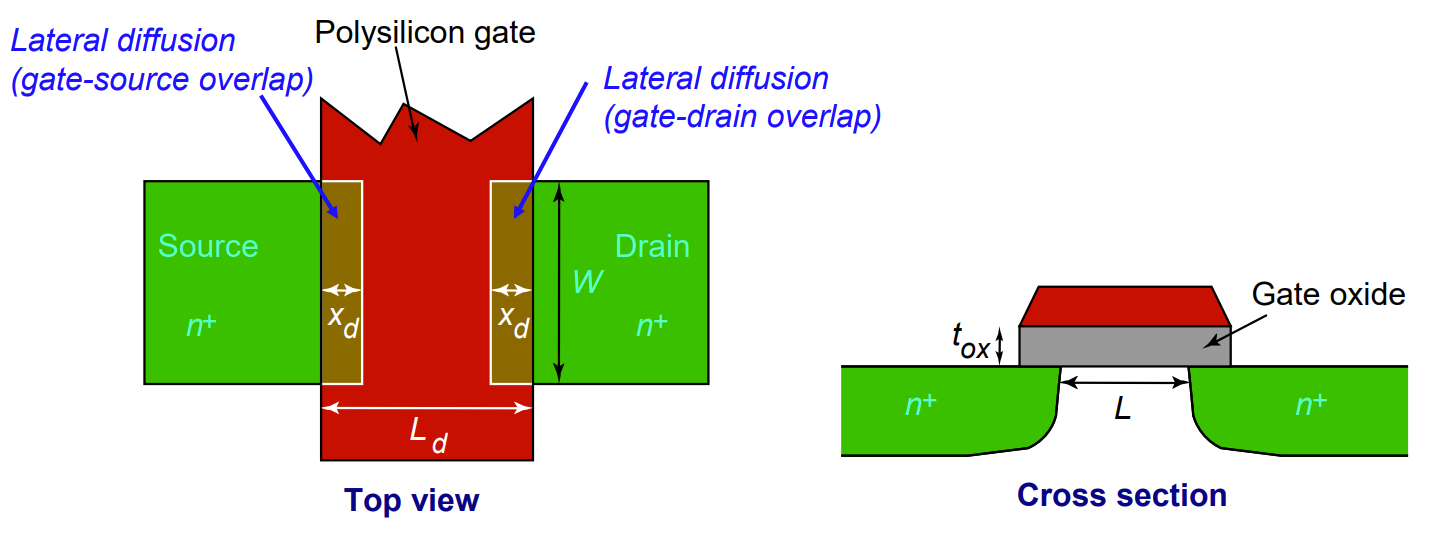
栅电容
扩散电容
其中
- $C_{SB}$ 是源区结电容
- $C_{jbs}$ 是单元区域衬底至源区底部结电容
- $C_{J}$ 是单元区域零偏压电容
- $C_{jbssw}$ 是单位周长衬底至源区侧壁结电容
- $C_{JSW}$ 是单位周长零偏压侧壁结电容
- $C_{jbsswg}$ 是单位周长衬底至源区栅边侧壁结电容
- $C_{JSWG}$ 是单位周长零偏压栅边侧壁结电容
- $AS$ 是源区底部面积
- $PS$ 是源区侧壁周长
- $\Phi_0$ 是内建电势
- $V_{sb}$ 是源和衬底间的电势
- $M_{J},M_{JSW},M_{JSWG}$ 是结缓变系数
阈值压降
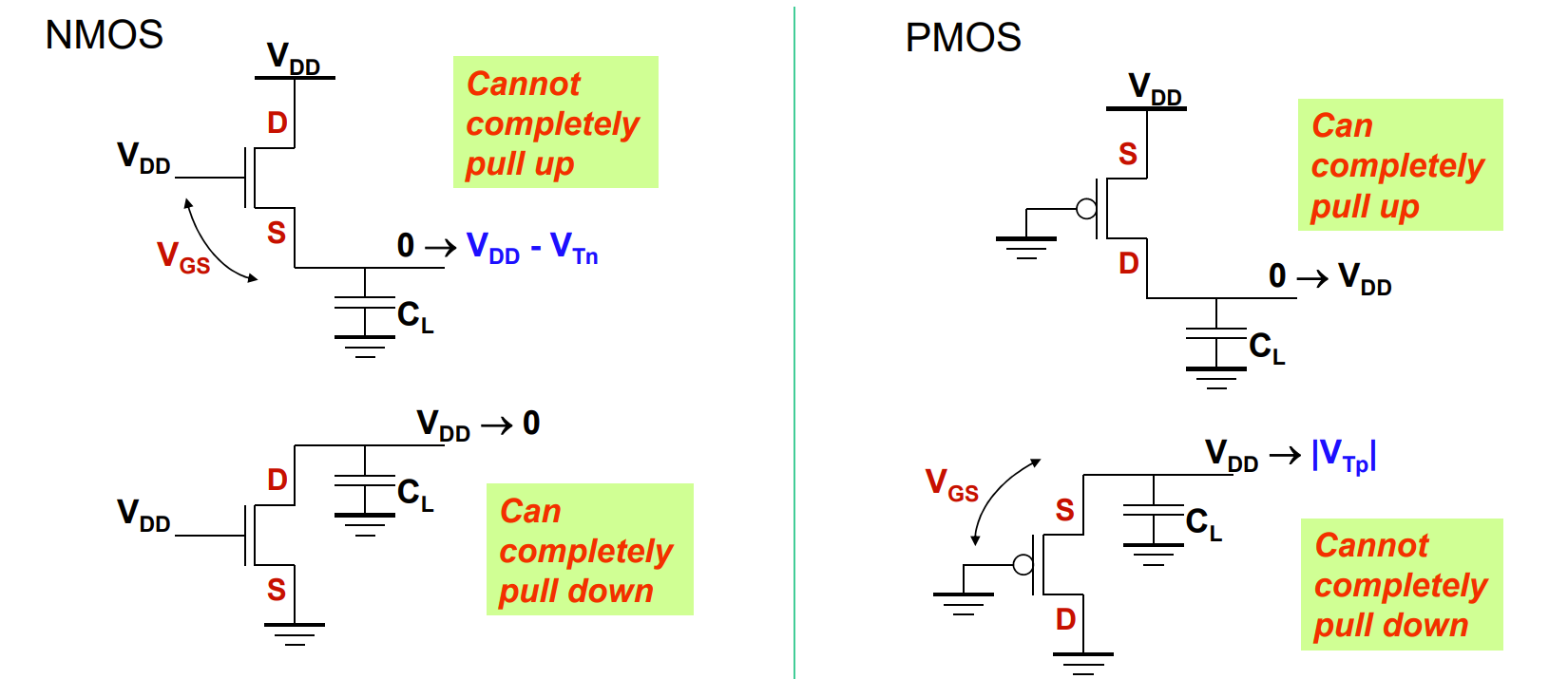
- NMOS Transistors pass a “strong” 0 but a “weak” 1
- PMOS Transistors pass a “strong” 1 but a “weak” 0
- NMOS 不能被完全上拉,可以被完全下拉
- PMOS 不能被完全下拉,可以被完全上拉
体偏效应
其中体效应系数
费米电势
- 对于NMOS
- 正体偏,$V_{SB}<0$,$V_T$ 减小
- 负体偏,$V_{SB}>0$,$V_T$ 增大
- 对于PMOS
- 正体偏,$V_{SB}>0$,$V_T$ 增大
- 负体偏,$V_{SB}<0$,$V_T$ 减小(数值减小,绝对值增大)
第五章 反相器
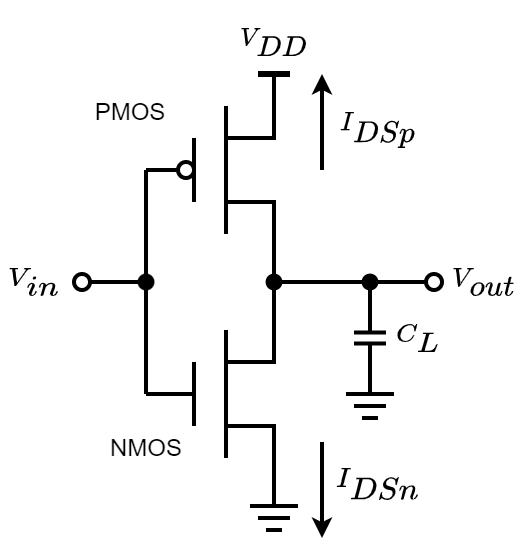
人工分析的统一模型
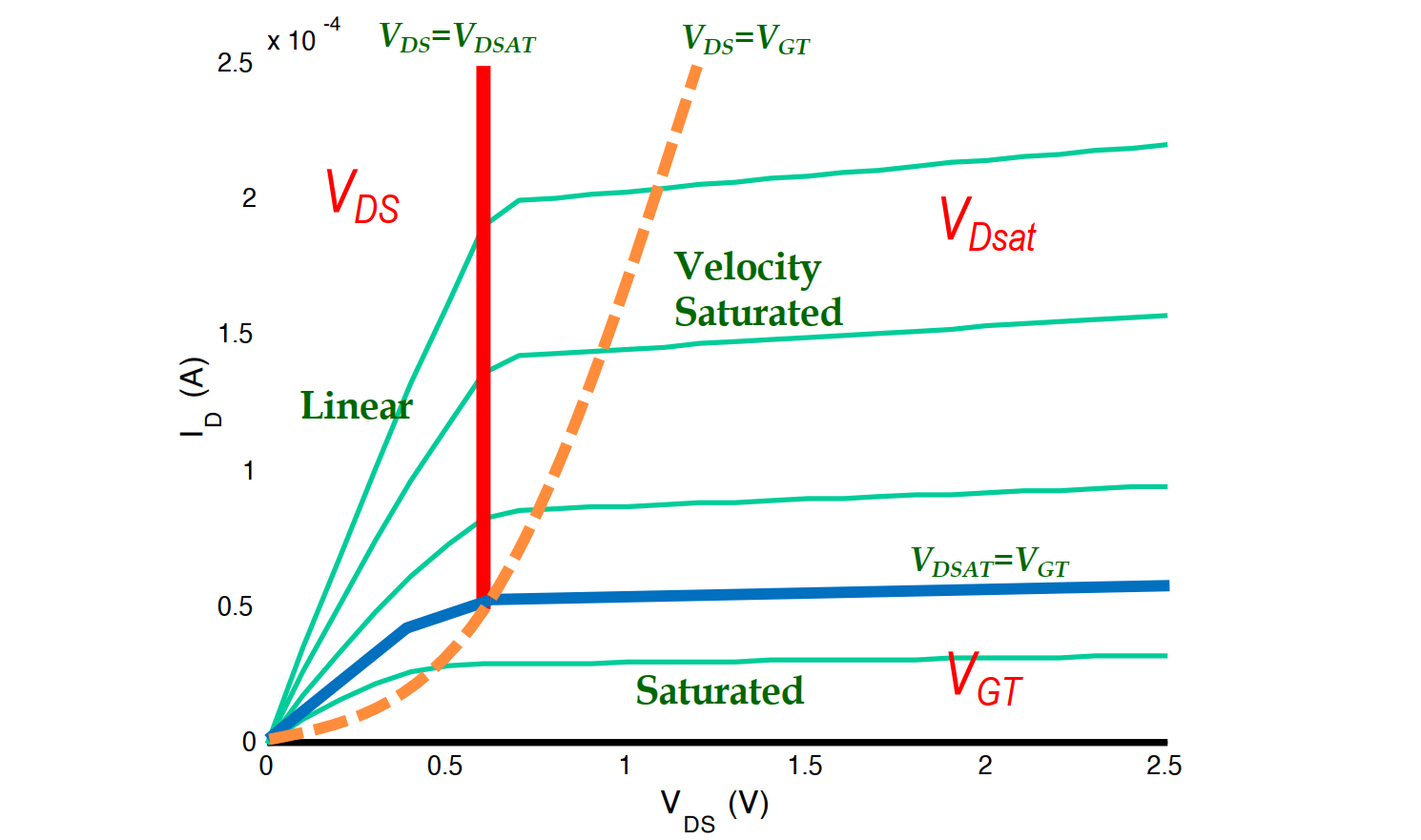
| 类型 | $V_{T0}$ | $\gamma$ | $V_{Dsat}$ | $k’$ | $\lambda$ |
|---|---|---|---|---|---|
| NMOS | 0.43 | 0.4 | 0.63 | 115e-6 | 0.06 |
| NMOS | -0.4 | -0.4 | -1 | -30e-6 | -0.1 |
静态CMOS反相器特性
- 输出高电平和低电平分别为 VDD 和 GND。换言之,电压摆幅等于电源电压。因此噪声容限很大。
- 逻辑电平与器件的相对尺寸无关,所以晶体管可以采用最小尺寸。具有这一特点的门称为无比逻辑。它不同于有比逻辑,在有比逻辑中逻辑电平是由组成逻辑的晶体管的相对尺寸来决定的。
- 稳态时在输出和 VDD 或 GND 之间总存在一条具有有限电阻的通路。因此一个设计良好的 CMOS 反相器具有低输出阻抗,这使它对噪声和干扰不敏感。输出电阻的典型值在 $k\Omega$ 的范围内。
- CMOS 反相器的输入电阻极高,因为一个 MOS 管的栅实际上是一个完全的绝缘体,因此不取任何 DC(直流)输入电流。由于反相器的输入节点只连到晶体管的栅上,所以稳态输入电流几乎为零。
- 理论上,单个反相器可以驱动无穷多个门(或者说具有无穷大的扇出)而仍能正确工作,但我们很快会看到增加扇出也会增加传播延时。尽管扇出不会对稳态特性有任何影响,但它使瞬态响应变差。
- 在稳态工作情况下电源线和地线之间没有直接的通路(即此时输入和输出保持不变)。没有电流存在(忽略漏电流)意味着该门并不消耗任何静态功率。
VTC(电压传输特性)
电压传输特性(VTC)的性质和形状可以通过图解法迭加 $NMOS$ 和 $PMOS$ 器件的电流特性来得到。这样的一个图形结构通常称为负载曲线图。它要求把 $NMOS$ 和 $PMOS$ 器件的 $I-V$ 曲线转换到一组公共坐标上。我们以输入电压 $V_{i \pi}$、输出电压 $V_{\mathrm{out}}$ 和 $NMOS$ 漏电流 $I_{D N}$ 作为选择的变量,于是 $PMOS$ 的 $I-V$ 关系就可以通过以下关系转换到这一变量空间中(下标 $n$ 和 $p$ 分别表示 $NMOS$ 和 $PMOS$ 器件):
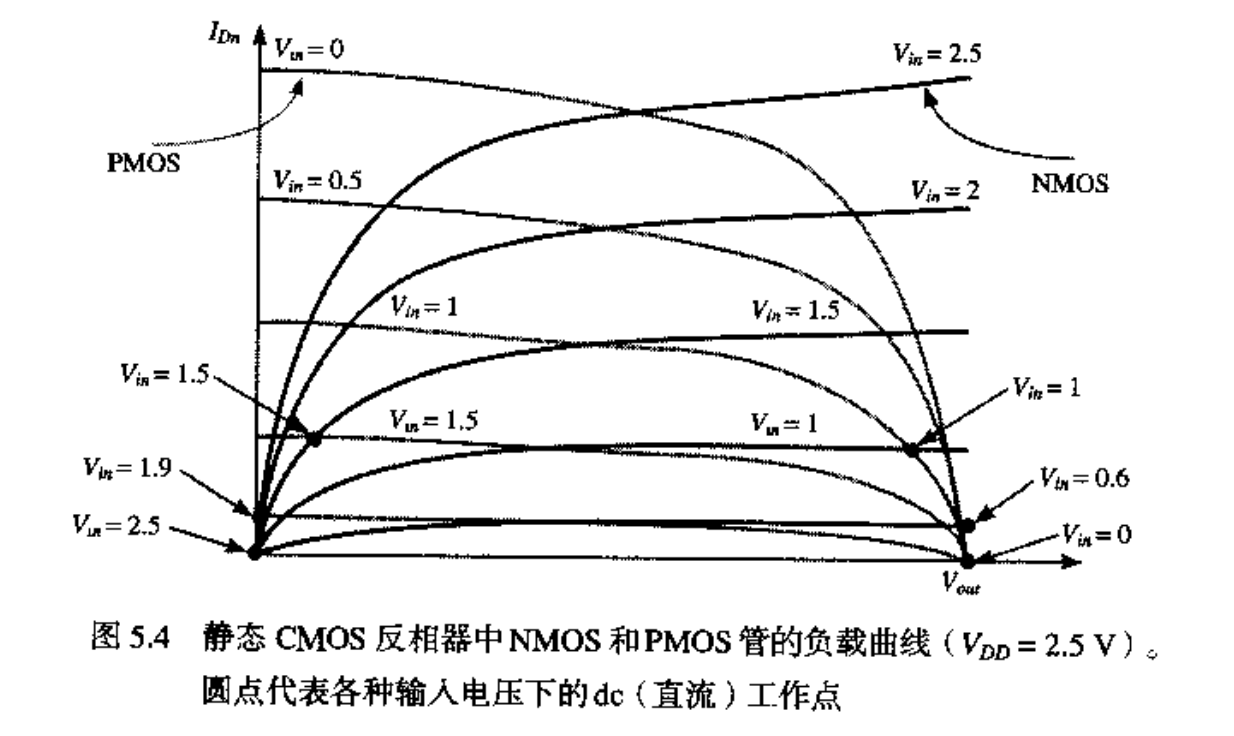
理想CMOS反相器的VTC: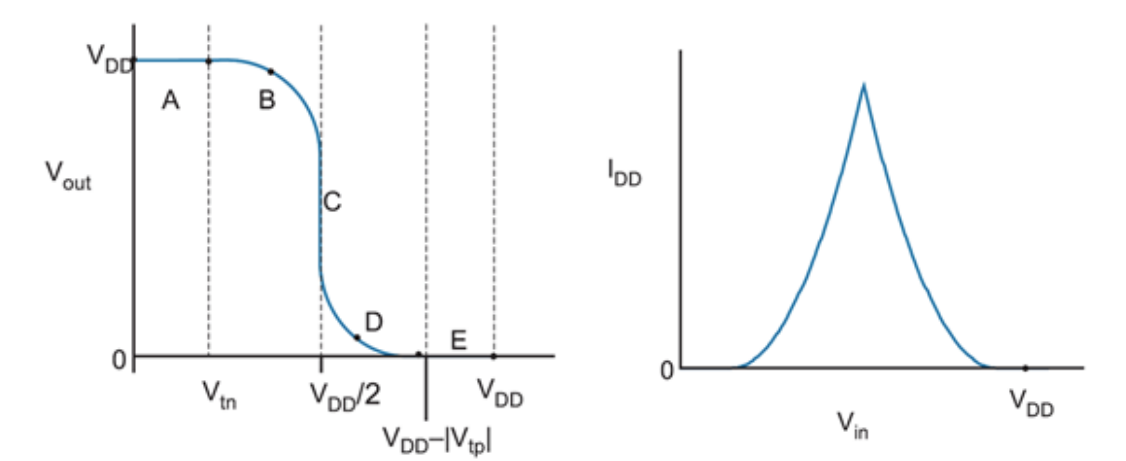
| 区域 | 条件 | PMOS | NMOS | 输出 |
|---|---|---|---|---|
| A | $[0,V_{Tn}]$ | 线性 | 截止 | $V_{DD}$ |
| B | $[V_{Tn},V_{DD}/2]$ | 线性 | 饱和 | $>V_{DD}/2$ |
| C | $V_{DD}/2$ | 饱和 | 饱和 | $X$ |
| D | $[V_{DD}/2,V_{DD}-\mid V_{Tp}\mid]$ | 饱和 | 线性 | $<V_{DD}/2$ |
| E | $[V_{DD}-\mid V_{Tp}\mid,V_{DD}]$ | 截止 | 线性 | $0$ |
考虑速度饱和的工作状态:
| 类型 | 工作区 | 条件 |
|---|---|---|
| PMOS | 饱和 | $V_{in}-V_{DD}-V_{tp}>V_{dsatp}$ |
| PMOS | 速度饱和 | $V_{in}-V_{DD}-V_{tp}<V_{dsatp}$ |
| PMOS | 线性 | $V_{out}>V_{DD}+V_{dsatp}$ |
| NMOS | 饱和 | $V_{in}-V_{tn}<V_{dsatn}$ |
| NMOS | 速度饱和 | $V_{in}-V_{tn}>V_{dsatn}$ |
| NMOS | 线性 | $V_{out}<V_{dsatn}$ |
阈值电压
开关阈值 $V_{M}$ 定义为 $V_{in}=V_{out}$ 的点,其值可以用图解法由 VTC 与直线 $V_{in}=V_{out}$ 的交点求得。在这一区域由于 $V_{DS}=V_{GS}$,PMOS 和 NMOS 总是饱和的。使通过两个晶体管的电流相等就可以得到 $V_{M}$ 的解析表达式。我们求解的情形是电源电压足够高,所以这两个器件可以被假设为都处于速度饱和(即 $V_{D S A T}<V_{M}-V_{T}$)。同时我们忽略沟长调制效应,于是有:
求解 $V_{M}$ 得到:
其中
- 为了让 $V_{M}$ 接近 $V_{DD}/2$,$\gamma$ 应该在 3~4 之间
增益
若
- 尺寸比增大
- $V_{DD}$ 减小
则增益增大
噪声容限
注意 $g$ 是负数
DC robust
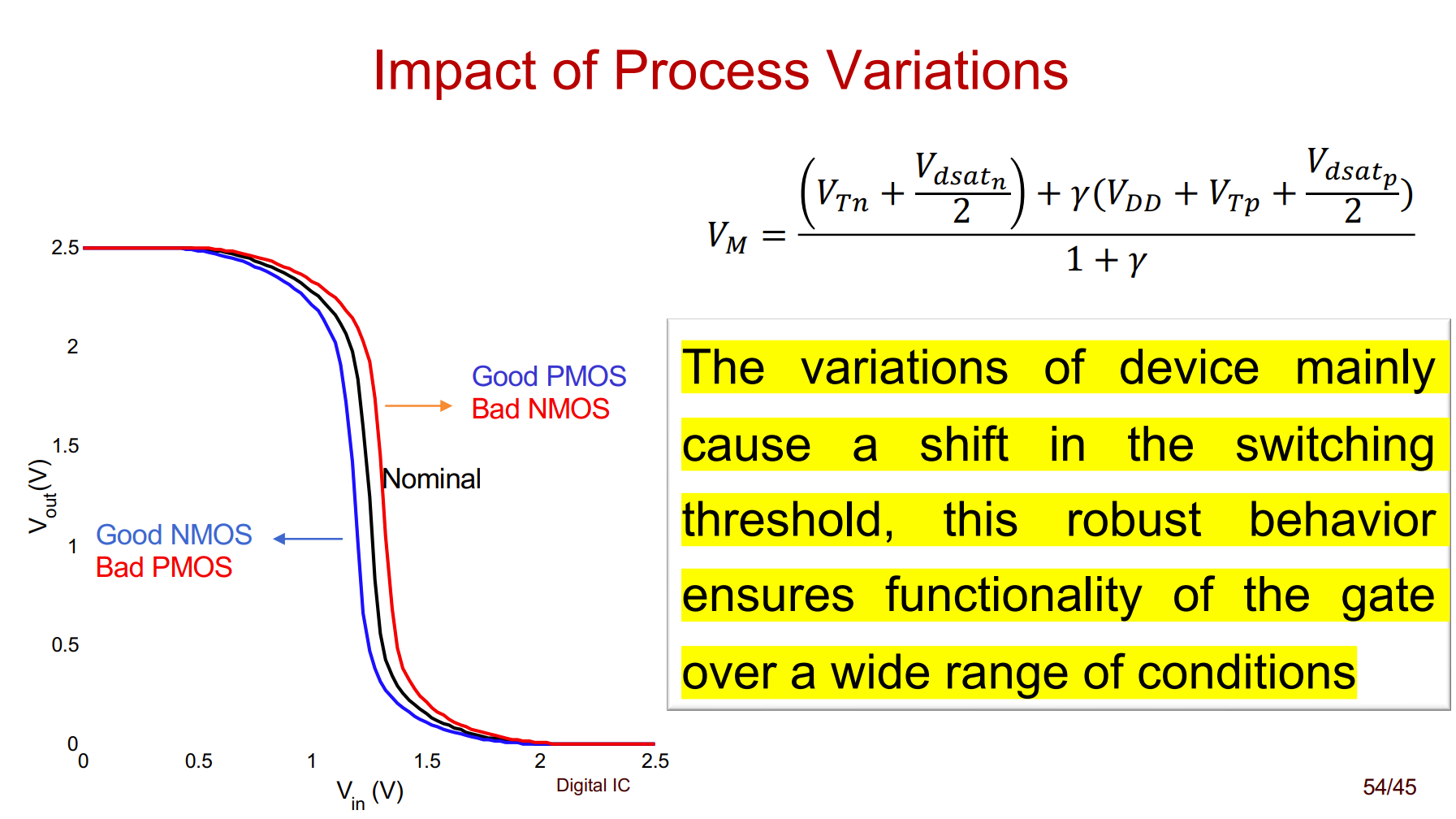
就是工艺角问题
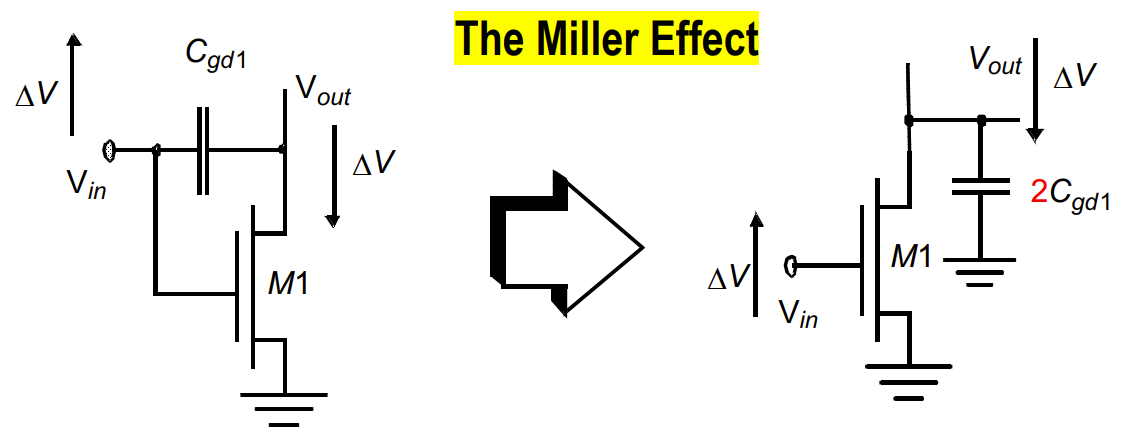
密勒效应
如果一个电容器的两个端子出现相同但相反的电压波动,可以用一个对地电容器来代替,其值是原值的两倍。
动态特性:电容
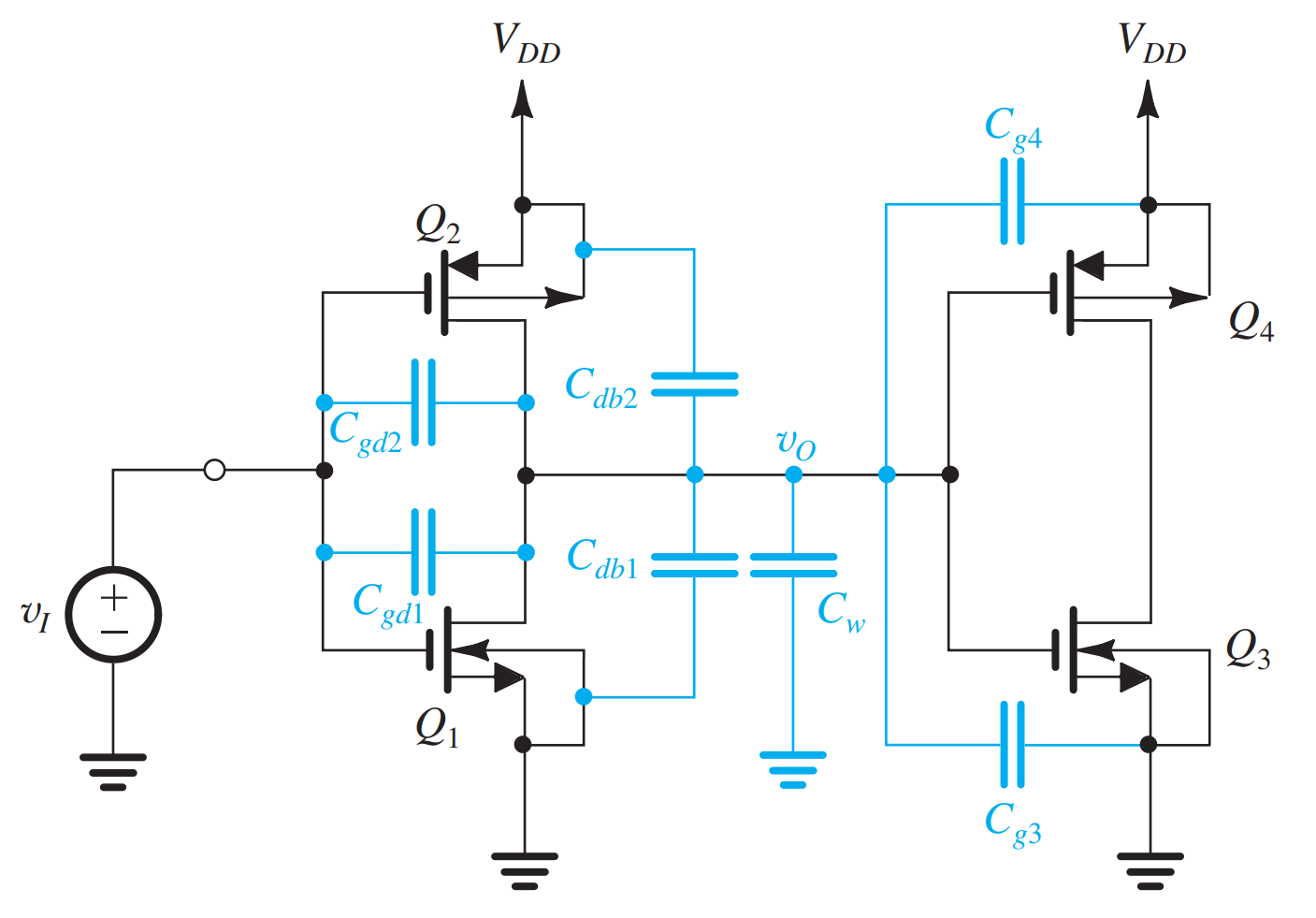
动态特性:电阻
MOS管的平均导通电阻
动态特性:传播延时
由高至低翻转的传播延时
由低至高翻转的传播延时
式中,$R_{\mathrm{eqp}}$ 是 PMOS 管在所关注时间内的等效导递电阻。
反相器的总传播延时定义为这两个值的平均:
人们常常希望一个门对于上升和下降输入具有相同的传播延时。这一状况可以通过使 NMOS 和 PMOS 晶体管的导通电阻近似相等来实现。
减小一个门的传播延时:
- 减小 $C_L$:注意这个负载电容由三个主要部分组成:门本身的内部扩散电容、互连线电容和扇出电容。细致的版图设计有助于减少扩散电容和互连线电容。优秀的设计实践要求漏扩散区的面积越小越好。
- 增加晶体管的 $W/L$ 比:这是设计者手中最有力和最有效的性能优化工具。但是在采用这一方法时要当心。增加晶体管尺寸也增加扩散电容,因而增加了 $C_L$。事实上,一旦本征电容(即扩散电容)开始超过由连线和扇出形成的外部负载,增加门的尺寸就不再对减少延时有帮助。它只是加大了门的面积,这称为自载效应。此外,较宽的晶体管具有较大的栅电容,这就增加了驱动门的扇出系数,从而又反过来影响它的速度
提高 $V_{DD}$:一个门的延时可以通过改变电源电压来调整。这一灵活性使设计者可以用能量损耗来换取性能,正如我们在后面一节中将要看到的那样。然而,增加电源电压超过一定程度后改善就会非常有限,因而应当避免。同时对可靠性方面的考虑(氧化层的击穿、热电子效应)也迫使在深亚微米工艺中对电源电压要规定严格的上限
最小延迟时,$\beta=\sqrt{\gamma}\approx 1.5$
- 上升下降延迟相同时,$\beta=\gamma\approx 2.4$
- 阈值电压是 $V_{DD}$ 的一半时,$\beta=3.5$
反相器链
尺寸系数
- 尺寸系数 $S$ 把反相器的晶体管尺寸与一个参考门(通常是一个最小尺寸的反相器)的晶体管尺寸联系起来。
- 本征电容 $C_{\mathrm{int}}=S C_{\mathrm{iref}}$
- 电阻 $R_{e q}=R_{\mathrm{ref}} / S$
- 反相器的本征延时 $t_{p 0}$ 与门的尺寸无关,而只取决于工艺及反相器的版图
- 使 $S$ 无穷大将达到最大可能的性能改善,因为这消除了任何外部负载的影响,使延时减小到只有本征延时值。当然尺寸并不能做到无限大。
传播延时
N级级联最佳方案
最佳级数N
上升下降时间修正
能量
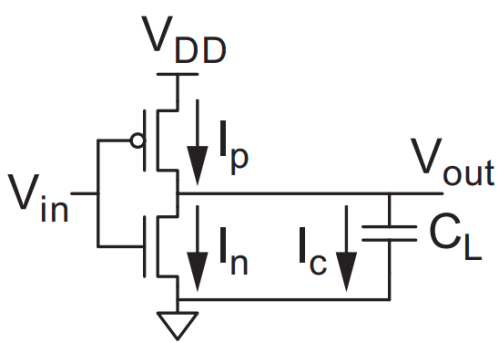
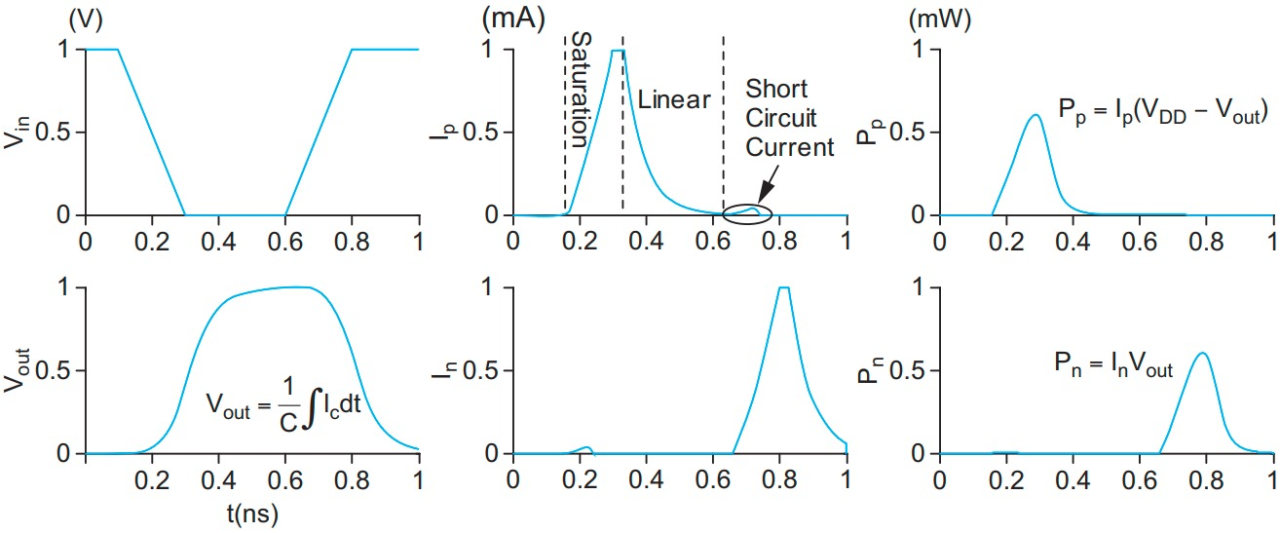
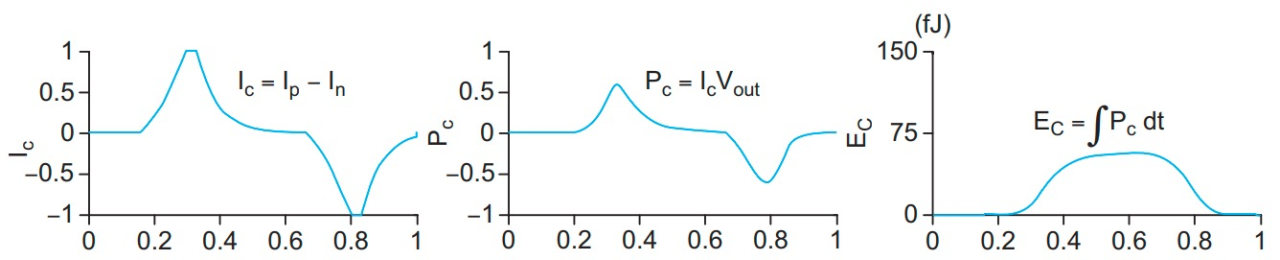
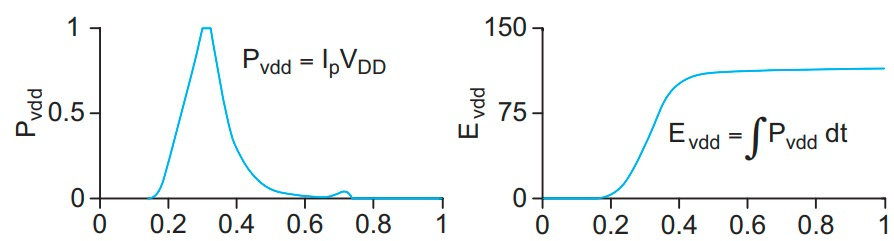
其中
- Capacitance $C_{L}$ 是扇出、导线长度、晶体管大小的函数
- Supply Voltage $V_{D D}$
- Activity factor $P_{0 \rightarrow 1}$ 是平均每个周期输出从0到1变化的次数
- Clock frequency $f$
门电路的能量(Activity factor)
对于具体的门电路,也是考虑输出从 0 到 1 变化的频率,此时可假设输入信号是 $\{0,1\}$ 随机信号
| 门类型 | 输入端口 | 输出 0 的概率 | 输出 1 的概率 | 功耗 |
|---|---|---|---|---|
| 反相器 | $1$ | $1/2$ | $1/2$ | $\frac{1}{4}CV_{dd}^2f$ |
| 与门 | $N$ | $1-\frac{1}{2^N}$ | $\frac{1}{2^N}$ | $\frac{2^N-1}{2^{N+1}}CV_{dd}^2f$ |
| 与非门 | $N$ | $\frac{1}{2^N}$ | $1-\frac{1}{2^N}$ | $\frac{2^N-1}{4^{N}}CV_{dd}^2f$ |
| 或门 | $N$ | $\frac{1}{2^N}$ | $1-\frac{1}{2^N}$ | $\frac{2^N-1}{4^{N}}CV_{dd}^2f$ |
| 或非门 | $N$ | $1-\frac{1}{2^N}$ | $\frac{1}{2^N}$ | $\frac{2^N-1}{4^{N}}CV_{dd}^2f$ |
| 异或门 | $N$ | $1/2$ | $1/2$ | $\frac{1}{4}CV_{dd}^2f$ |
短路电流
第四章 导线
概述
集成电路的导线已形成了一个复杂的几何形体,它引起电容、电阻和电感等寄生参数效应。所有这三个寄生参数对于电路的特性都会有多方面的影响:
- 它们都会使传播延时增加,或者说相应于性能的下降
- 它们都会影响能耗和功率的分布
- 它们都会引起额外的噪声来源,从而影响电路的可靠性
完整的导线等效模型非常复杂,好在常常可以进行相当多的简化,包括以下几点:
- 如果导线的电阻很大——例如截面很小的长铝导线的情形,或者外加信号的上升和下降时间很慢,那么电感的影响可以忽略
- 当导线很短,导线的截面很大,或者所采用的互连材料电阻率很低时,那么就可以采用只含电容的模型
- 当相邻导线间的间距很大,或者当导线只在一段很短的距离上靠近在一起的时候,导线相互间的电容可以被忽略,并且所有的寄生电容都可以模拟成接地电容
电容
首先考虑一条简单的矩形导线放在半导体衬底之上,如下图所示。如果这条导线的宽度明显大于绝缘材料的厚度,那么就可以假设电场线垂直于电容极板,并且它的电容可以用平行板电容模型(平面电容)来模拟。在这些情况下该导线的总电容可以近似为:
其中
- $W$ 和 $L$ 分别是导线的宽度和长度
- $t_{di}$ 和 $\varepsilon_{di}$ 分别表示绝缘层的厚度和它的介电常数,$\varepsilon_{di}=\varepsilon_{r}\varepsilon_{0}$
- 因此 low-k 材料可以降低导线间电容
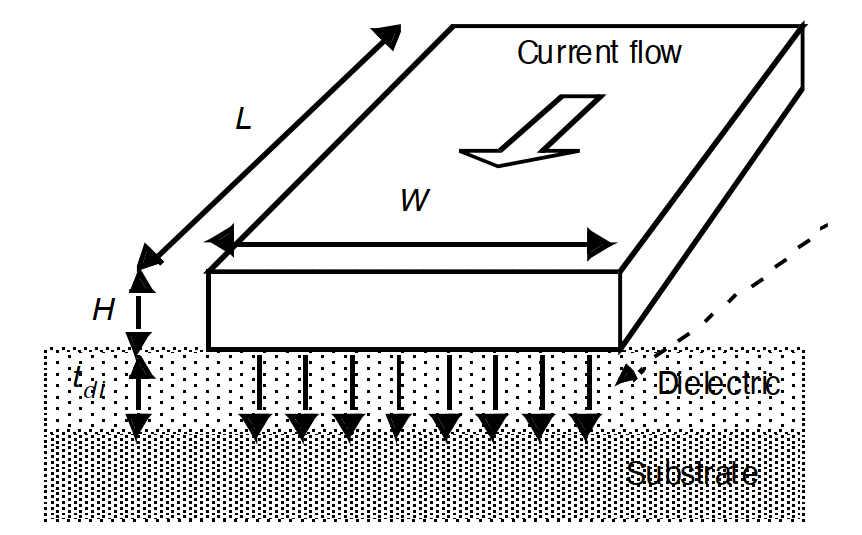
但是,当宽度接近高度甚至小于高度的时候,这个模型不再准确,因为侧壁也会有电容。我们采用一个简化的模型把这个电容近似为两部分的和:一个平板电容由宽度为 $W$ 的一条导线与接地平面之间的垂直电场决定,以及一个边缘电容用一条直径等于互连线宽度 $H$ 的圆柱形导线来模拟。于是得到
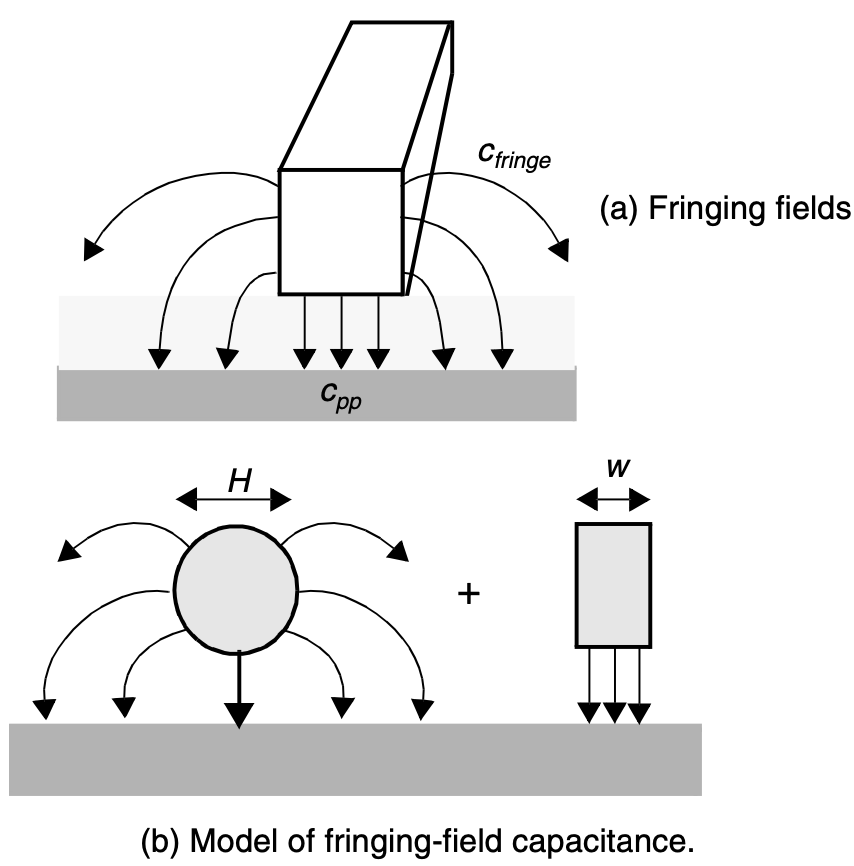
(当导线宽度越大,电容越接近平板电容的值)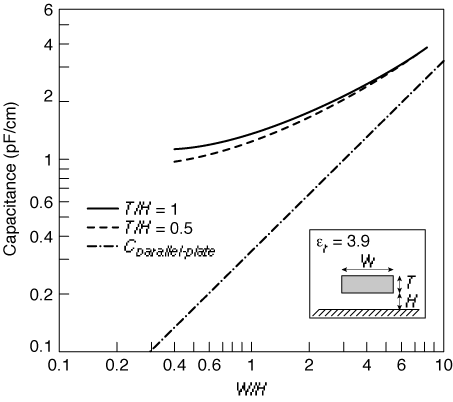
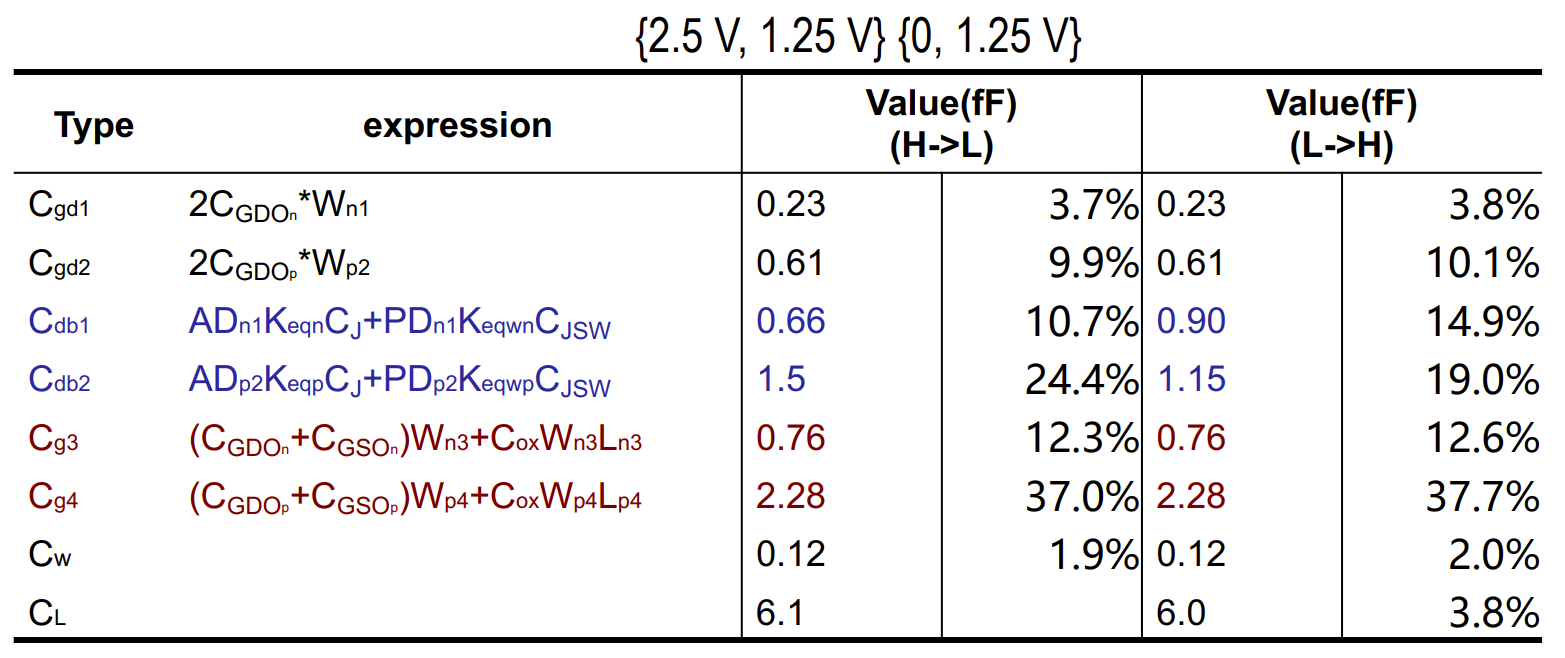
0.25um CMOS 工艺电容计算
平面电容:(行代表上极板,列代表下极板,单位:$\mathrm{aF}/\mathrm{\mu m}^2$)
| 场氧 Field | 有源区 Active | 多晶 Poly | Al1 | Al2 | Al3 | Al4 | |
|---|---|---|---|---|---|---|---|
| 多晶 | 88 | ||||||
| Al1 | 30 | 41 | 57 | ||||
| Al2 | 13 | 15 | 17 | 36 | |||
| Al3 | 8.9 | 9.4 | 10 | 15 | 41 | ||
| Al4 | 6.5 | 6.8 | 7 | 8.9 | 15 | 35 | |
| Al5 | 5.2 | 5.4 | 5.4 | 6.6 | 9.1 | 14 | 38 |
边缘电容:(单侧面,单位:$\mathrm{aF}/\mathrm{\mu m}$)
| 场氧 Field | 有源区 Active | 多晶 Poly | Al1 | Al2 | Al3 | Al4 | |
|---|---|---|---|---|---|---|---|
| 多晶 | 54 | ||||||
| Al1 | 40 | 47 | 54 | ||||
| Al2 | 25 | 27 | 29 | 45 | |||
| Al3 | 18 | 19 | 20 | 27 | 49 | ||
| Al4 | 14 | 15 | 15 | 18 | 27 | 45 | |
| Al5 | 12 | 12 | 12 | 14 | 19 | 27 | 52 |
线间电容:(单位:$\mathrm{aF}/\mathrm{\mu m}$)
| 多晶 Poly | Al1 | Al2 | Al3 | Al4 | Al5 |
|---|---|---|---|---|---|
| 40 | 95 | 85 | 85 | 85 | 115 |
电阻
铜阻挡层(copper barrier layer)和凹陷效应(dishing impact)
- 铜阻挡层(Copper Barrier Layer):在CMOS工艺中,金属层通常使用铜(Cu)作为导电材料。由于铜与硅(Si)之间的反应性,为了防止铜渗透到硅基底中,需要在铜层和硅基底之间添加一层称为铜阻挡层的材料。铜阻挡层通常使用钨(W)或钨合金等材料,其具有低扩散率特性,可以有效防止铜与硅的反应。
- 凹陷效应(Dishing Impact):在CMOS工艺中,当进行金属填充时,如铜填充,可能会出现凹陷效应。凹陷效应指的是在金属填充过程中,由于电流密度分布的不均匀性,金属在一些区域会过度填充,而在其他区域则会出现凹陷。这种凹陷现象可能会导致金属层的不平坦性增加,从而对电路性能产生负面影响,如信号传输的不稳定性和电阻变化等。
方块电阻
由于对给定的工艺 $H$ 是一个常数,所以电阻定义式可以重新写成:
式中
为材料的薄层电阻(Sheet resistance),其单位为 $\Omega /\square$。这表明,一个方块导体的电阻与它的绝对尺寸无关,为了得到一条导线的电阻,只需将薄层电阻乘以该导线的 $L/W$。
- 注意:如果给了图形,那么导线的90度转角处只能算半个square。
趋肤效应(skin effect)
趋肤效应(skin effect)是指高频电流在导体中的分布不均匀现象。当电流频率增加时,电流会倾向于集中在导体表面附近,而在导体内部的电流密度会减小。
趋肤效应会导致导体截面内部的有效导电区域减小,增加了电阻。定义趋肤深度
截面积就从 $WH$ 变成了
设计时优化
- 尽量不要缩放导线厚度(H)
- 铜(Cu)或硅化物做导线(更好的电导率)
- 低k材料(更低的电容)
- 更多的互连层
- 低层的薄密度
- 宽间隔较高层
串扰(crosstalk)
当导线 A 中的信号在 01 切换时,由于电容耦合(称为串扰),它往往会将邻近的导线 B 也带入其中。
Y 覆盖在 X 上,
其中
$C_{XY}$ 是 X 和 Y 的层间平面电容,$C_{Y}$ 是 Y 对衬底的层间平面电容
同层时,$C_{adj}$ 还需要一个系数 MFC,表示它与它相邻的线之间的变化差别。
aggressor-victim模型
对于 floating line,电压串扰同上公式
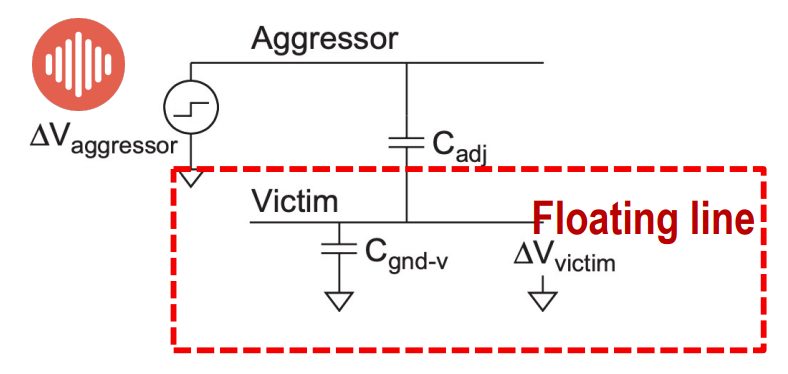
对于 driving line,需要加个修正因子 $\frac{1}{1+\kappa}$
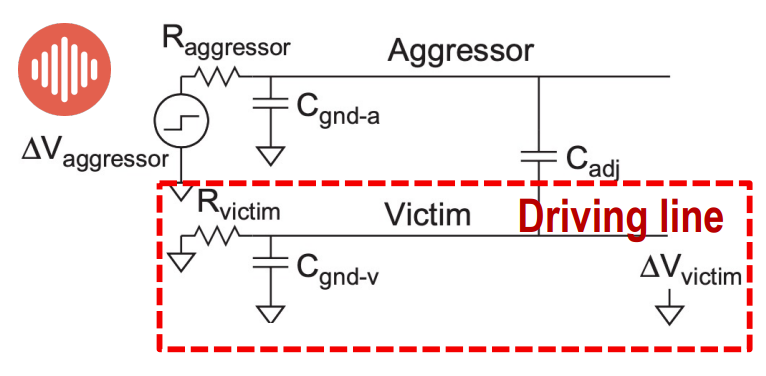
design tips
- 避免悬空节点和悬空线($\kappa=0$)
- 两条线不要并排走太长($C_{adj}$ 过大)
- 增加上升/下降时间能缓解串扰
- 使用差分信号
- 使用屏蔽层(两根信号之间加地线)
- 相邻两层信号纵横交错放置
- 对 aggressor 加反相器,使得串扰能够抵消
- 差分信号线时不时交换个位置,使得串扰能够抵消
集总C模型
只要导线的电阻部分很小并且开关频率较低,那么就可以很合理地只考虑该导线的电容部分,并把分布的电容集总为单个电容,如下图所示。注意在这一模型中导线仍表现为一个等势区,因而导线本身并不引人任何延时。对于性能的唯一影响是由电容对于驱动门的负载效应引起的。

若当 $V_{in}$ 是阶梯从 0 到 1 时,
其中
集总RC模型
类似集总C模型,微分方程为
输入阶梯信号,输出仍然是 RC 充电公式,其中
分布式模型

每一小部分的微分方程可以写为:
具体解略,不要求。但是可以给出一些关键节点的数值,见下面的表
RC网络的Elmore延迟
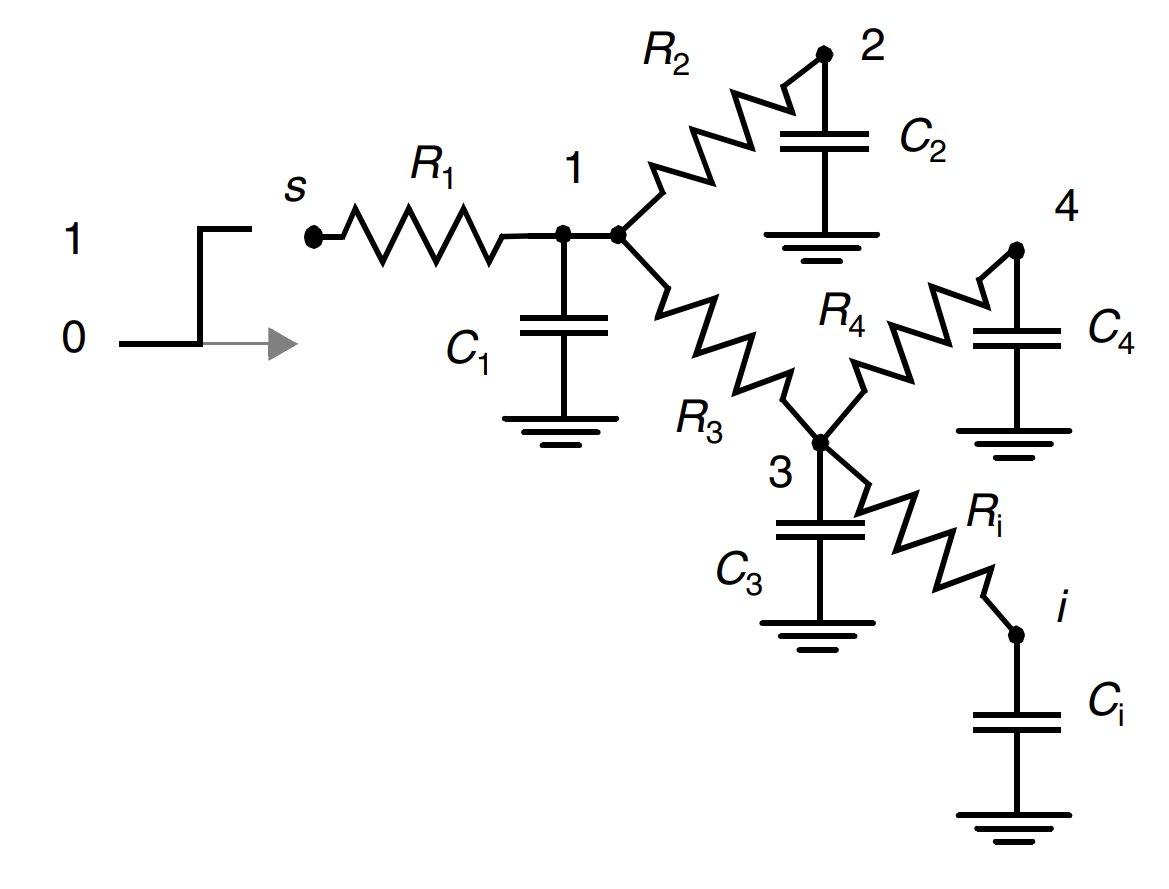
实际网络很复杂,不可能只有一个起点一个终点,而通常是 RC 网络。假设
- 只有一个输入节点
- 所有电容都是在节点和地之间
- 不包含电阻环路
设网络中起点是 s,终点是 i,定义共享路径电阻
那么遍历电容可以得到延迟:
也可以使用遍历电阻的方法:遍历 s 到 i 的所有电阻,乘以被这个电阻驱动的所有电容
Elmore模型的RC链

当 N 很大时
- 导线的延迟是其长度的二次函数!这意味着导线长度增加一倍,延迟就会增加两倍。
- 分布式 RC 线路的延迟是集总 RC 模型预测延迟的一半。这证实了前面的观点,即集总模型对电阻延迟的看法是悲观的。
加上驱动端和负载端的RC
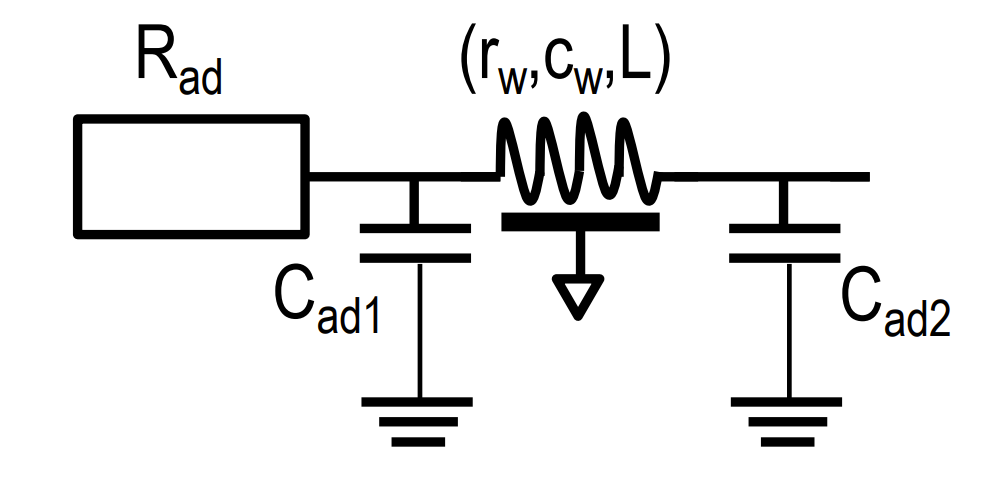
总结对比
| 电压变化 | 集总 RC 模型 | 分布式 RC 模型 | Elmore 模型 |
|---|---|---|---|
| $0\rightarrow 50\%(t_{p})$ | 0.69RC | 0.38RC | 0.345RC |
| $0\rightarrow 63\%(\tau)$ | RC | 0.5RC | 0.5RC |
| $10\%\rightarrow 90\%(t_{r})$ | 2.2RC | 0.9RC | 1.1C |
| $0\rightarrow 90\%$ | 2.3RC | 1.0RC | 1.15RC |
性能
- 长 Poly 线太慢,使用 Metal 线在两端驱动,或者分段并联
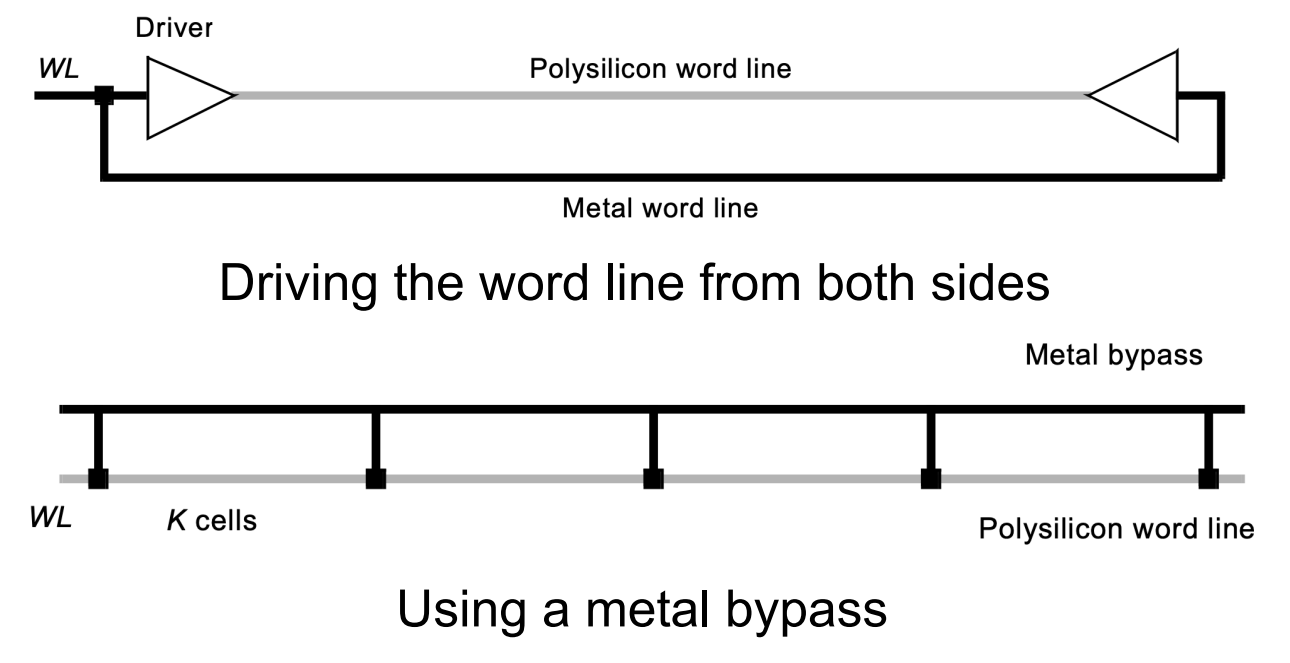
- 使用斜45°的互连线
- 插入反相器
若假设每个反相器延时都是 $t_{p \text {buf} 0}$一般情况,设反相器的电阻和电容为 $R_d$ 和 $C_d$,延时对 s 和 m 求偏导,得到最优解其中 $t_{\text {pbuff} 1}$ 是单位反相器推单位反相器的延时
第六章 组合逻辑
“互补”CMOS
静态 CMOS 逻辑门是两个网络的组合,分别称为上拉网络(PUN)和下拉网络(PDN)。PUN 的功能是在逻辑门输出为 1 时(基于输入),提供输出与 VDD 之间的连接。同样,PDN 的功能是在逻辑门输出为 0 时将输出连接至 VSS。PUN 和 PDN 网络以互斥的方式构建,因此在稳定状态下只有一个网络在导通。这样,一旦瞬态稳定下来,VDD 和输出 F 之间始终存在一条通路,实现高电平输出,或者,VSS 和 F 之间存在一条通路,实现低电平输出。这相当于说,输出节点在稳定状态下始终是一个低阻抗节点。
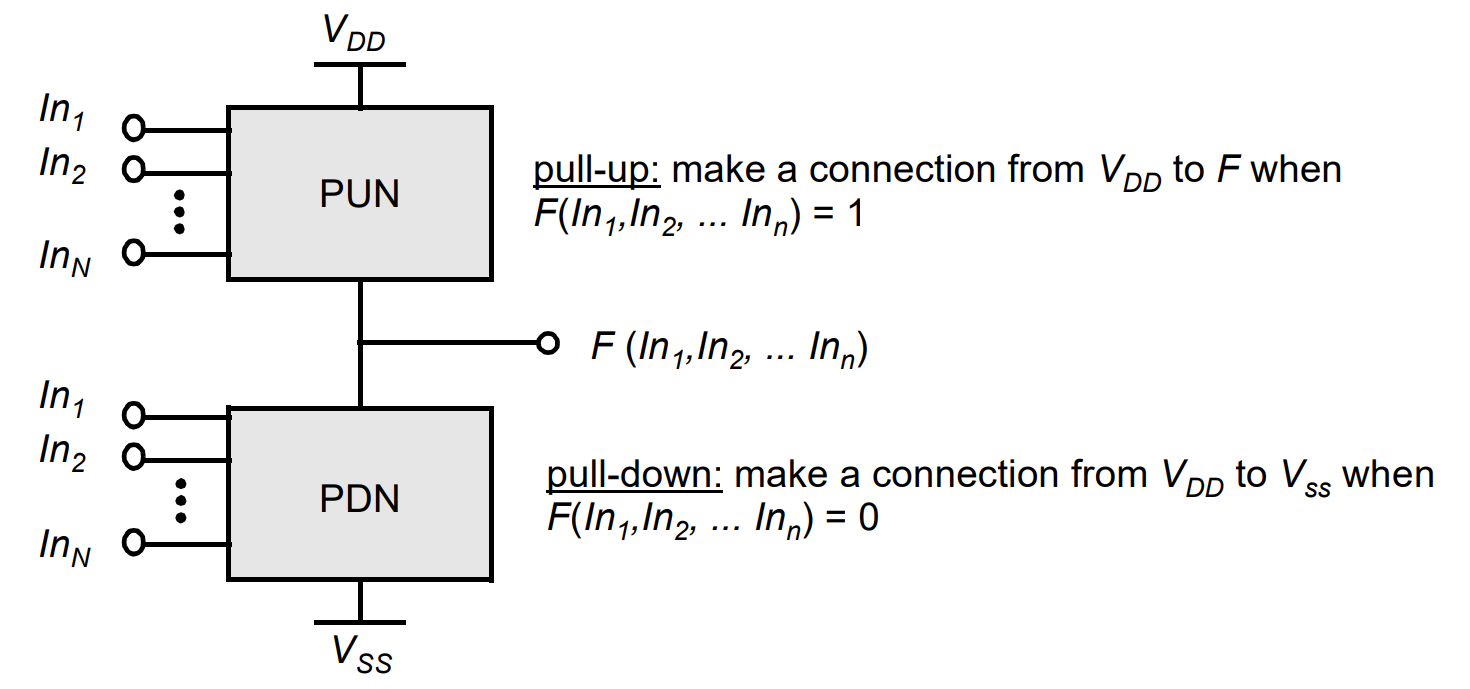
| 上拉网络 PUN | 下拉网络 PDN | |
|---|---|---|
| 组成 | PMOS | NMOS |
| 输出为 0 时 | 不工作 | 使 F 与 GND 连接 |
| 输出为 1 时 | 使 F 与 GND 连接 | 不工作 |
完整门电路画图
假设给定 $Y=\overline{f(A,B)}$,则
- 在 PDN 中画出 $f(A,B)$,加法并联,乘法串联
- 在 PUN 中画出 $f(A,B)$,加法串联,乘法并联
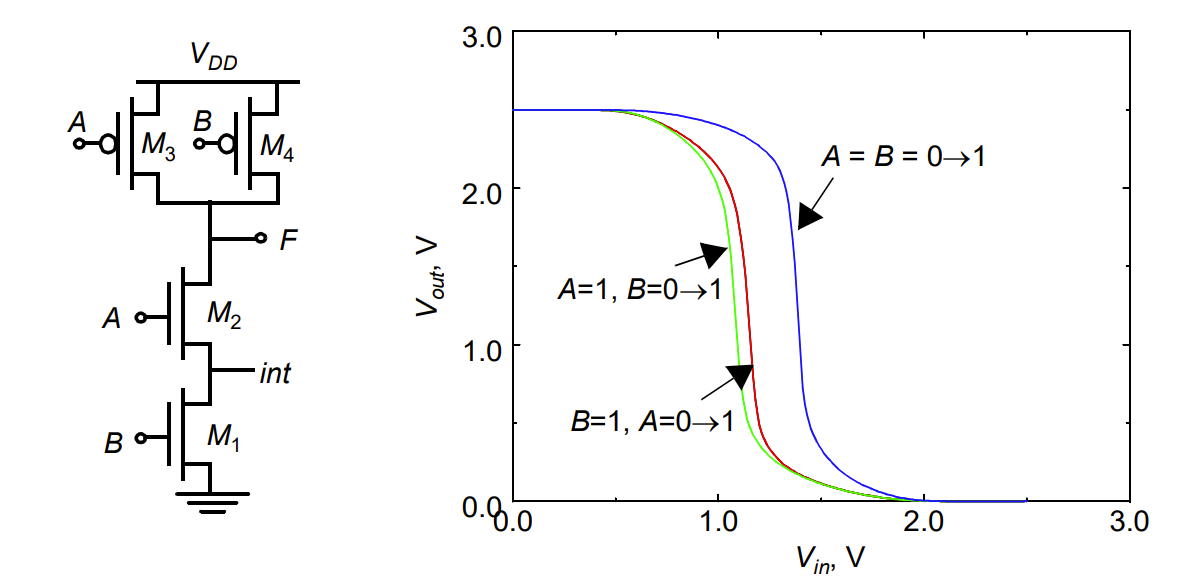
VTC
由于输入不对称和体偏效应的存在,VTC 是数据相关的。
延迟
- 由于网络复杂,输入情况不同,延迟不同
- 传播延时是最坏情况下的延时,污染延时是最好情况下的延时
- 有必要设计各个 MOSFET 的尺寸,使得 $t_{pLH}$ 和 $t_{pHL}$ 与一个最小尺寸反相器相同
尺寸规则
- 初始 PUN2 PDN1
- 分配下去:并联一样、串联加倍
数据相关的分析
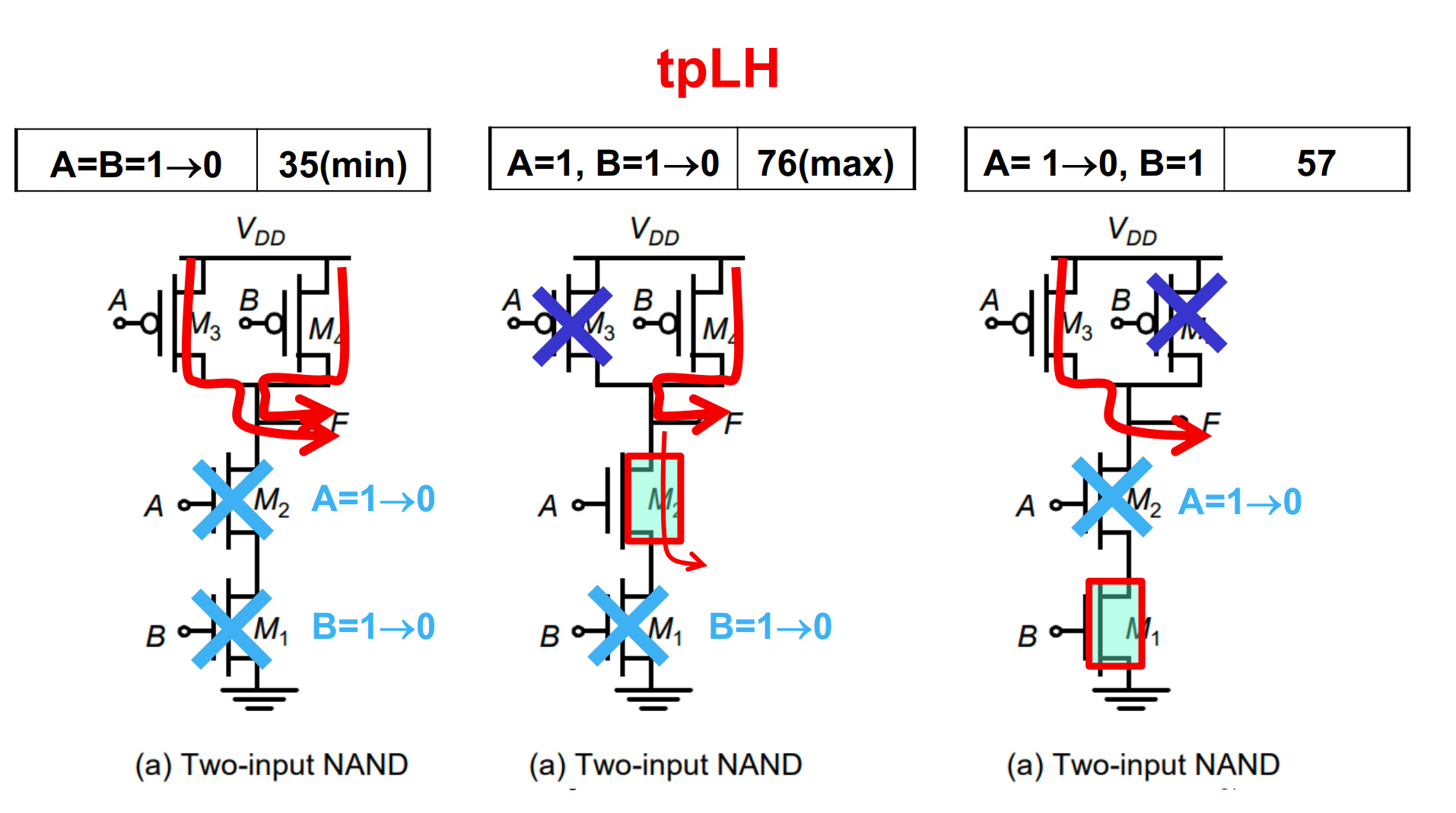
tpLH:
- $A=B=1\rightarrow 0$ 时,PDN 不通,两个 P 管给电容充电,速度最快
- $A=1,B=1\rightarrow 0$ 时,M2 导通,一个 P 管开启,电流一部分会经过 M2 给寄生电容充电,故最慢
- $A=1\rightarrow 0,B=1$ 时,M2 关闭,PDN 不通,一个 P 管开启
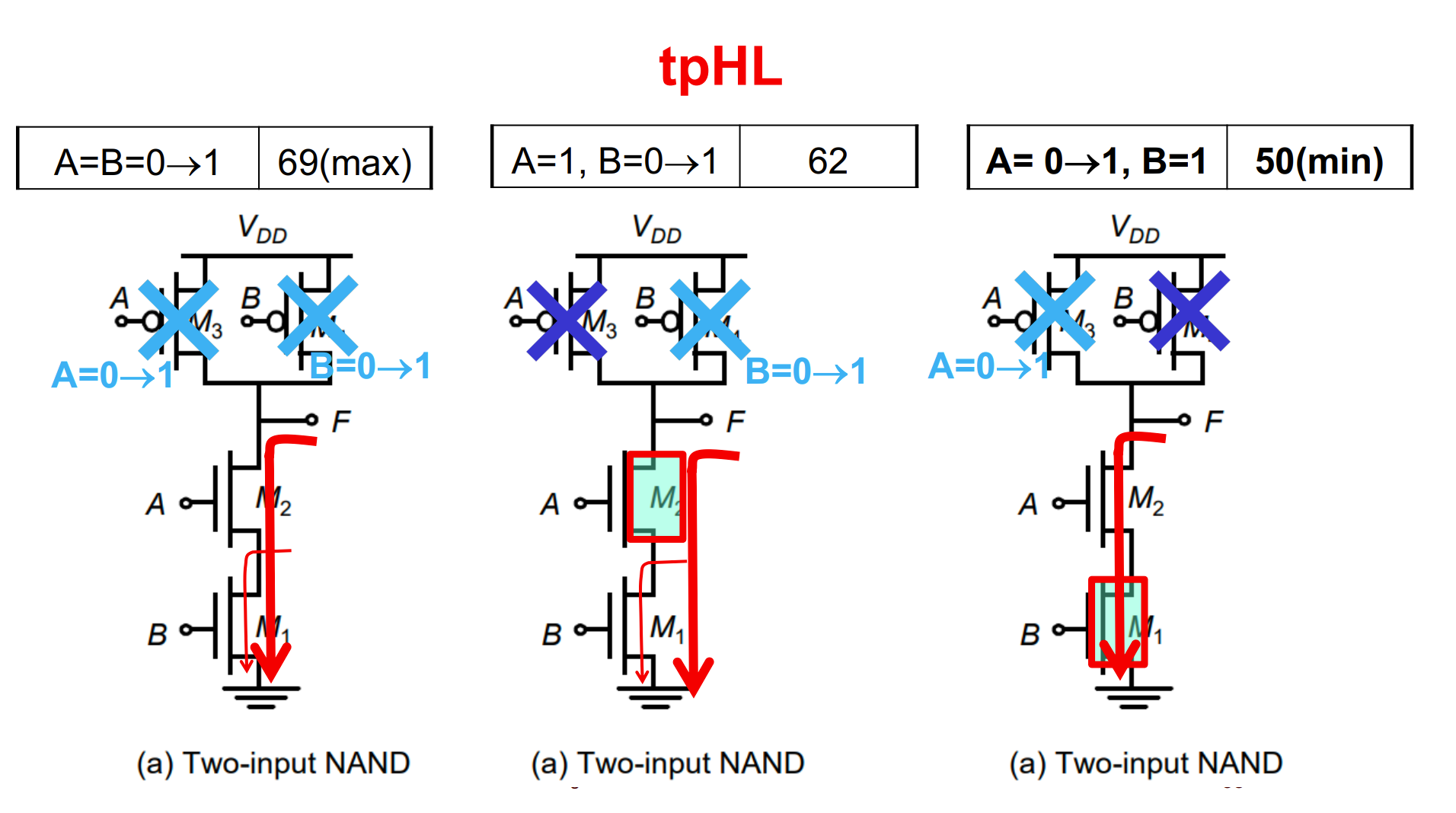
tpHL:
- $A=B=0\rightarrow 1$ 时,A、B 从截止开始转变到饱和,载流子分布、电阻降低需要时间,速度最慢
- $A=1,B=0\rightarrow 1$ 时,M2 导通,比上面的仅仅快了 M2 转换状态的时间
- $A=0\rightarrow 1,B=1$ 时,M1 导通,M1 与 M2 之间电容已经被放电,故最快
根据版图算延迟
(Todo)
根据逻辑电路图算延迟
以 2-input NAND 为例
大扇入优化
- 重排序:让先到来的信号放在 PDN 下面,先放电
- 逐级递增尺寸:串联电路,经常被计算到的电阻调小,离输出越近尺寸越小
- 重组逻辑:扇入不要超过4个
- 插入buffer隔离大扇出和大扇入
逻辑努力——组合网络延迟优化
以 NAND 为例
- 首先按照 resizing network rule 进行大小设置,保证输出的电阻 $R_{p a r-c l}$(最坏情况下的电阻)与单位反相器的输出电阻 $R_{par-inv}$ 相同。
- $C_{par-inv}$ 表示单位反相器的寄生电容(输出电容),$C_{par-cl}$ 表示
- NAND 整体尺寸扩大到原来的 $x_i$ 倍,$R_{par-cl}$ 变为原来的 $1/x_{i}$,$C_{par-cl}$ 又变为原来的 $x_i$ 倍。改记原来的电容和电阻为 $C_{par-cl-0}$、$R_{par-cl-0}$,所以有 $C_{par-cl}=x_{i}C_{par-cl-0}$、$R_{par-cl}=R_{par-cl-0}/x_{i}$
传播延迟
其中:
- $t_{p0}$ 是单位反相器的本征延迟
- $p$ 是本征延迟比,是单位大小逻辑门寄生(输出)电容比上单位反相器的寄生(输出)电容
- $g$ 称为逻辑努力,是单位大小逻辑门输入电容比上单位反相器的输入电容(通常是3)
- $f$ 称为电气努力,是外部负载电容比上放大后逻辑门输入电容
- $h=gf$ 称为门努力,是外部负载电容比上单位反相器的输入电容再除以逻辑门放大倍数
栅极的逻辑努力定义为栅极的输入电容与能提供相同输出电流的反相器的输入电容之比,对于给定负载,复杂栅极必须比反相器更努力地工作,才能产生类似的响应。
两种标注法
1、标在一输入端表示输入端电容与单位反相器输入电容的比值,也就是 $C_{g-cl}/C_{g-inv}$
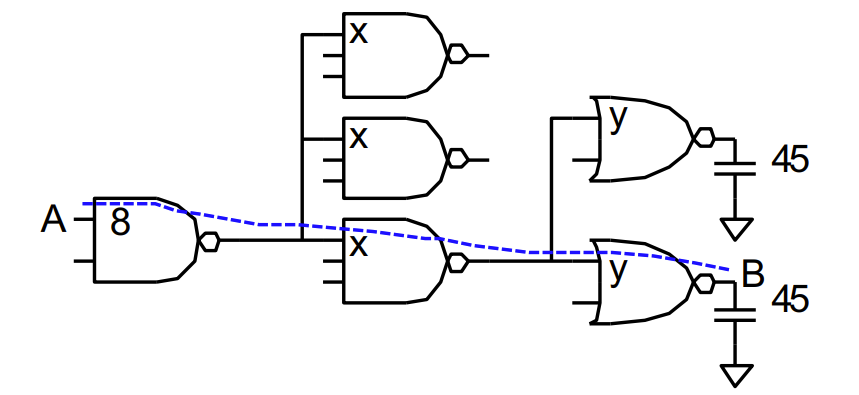
2、标在逻辑门上表示整个逻辑门的放大倍数,也就是 $C_{par-cl}/C_{par-cl-0}=x_{i}$
常见门电路的逻辑努力
| 输入数 | 2 | 3 | 4 | n |
|---|---|---|---|---|
| NAND | 4/3 | 5/3 | 6/3 | (n+2)/3 |
| NOR | 5/3 | 7/3 | 9/3 | (2n+1)/3 |
MUX:$(2N+(\log_2 N)+1)|3$
优化电路延时
注意此处的 f 代表组合网络总体的放大系数
当然,对于组合逻辑,不可能只是一条线,中间一定还有分支需要去驱动,所以修正
令
则最优条件
功耗
其中 $\alpha_i$ 是活跃因子,$p_i$ 是本征延迟比
简单二输入门的活跃因子
| $p_1$ | $\alpha_{0 \rightarrow 1}$ | |
|---|---|---|
| AND2 | $p_Ap_B$ | $(1-p_1)p_1$ |
| AND3 | $p_Ap_Bp_C$ | |
| OR2 | $1-\bar{p}_A\bar{p}_B$ | |
| NAND2 | $1-p_Ap_B$ | |
| NOR2 | $\bar{p}_A\bar{p}_B$ | |
| XOR | $p_A\bar{p}_B+\bar{p}_Ap_B$ |
- 输入必须独立
- 电路没有反馈
毛刺
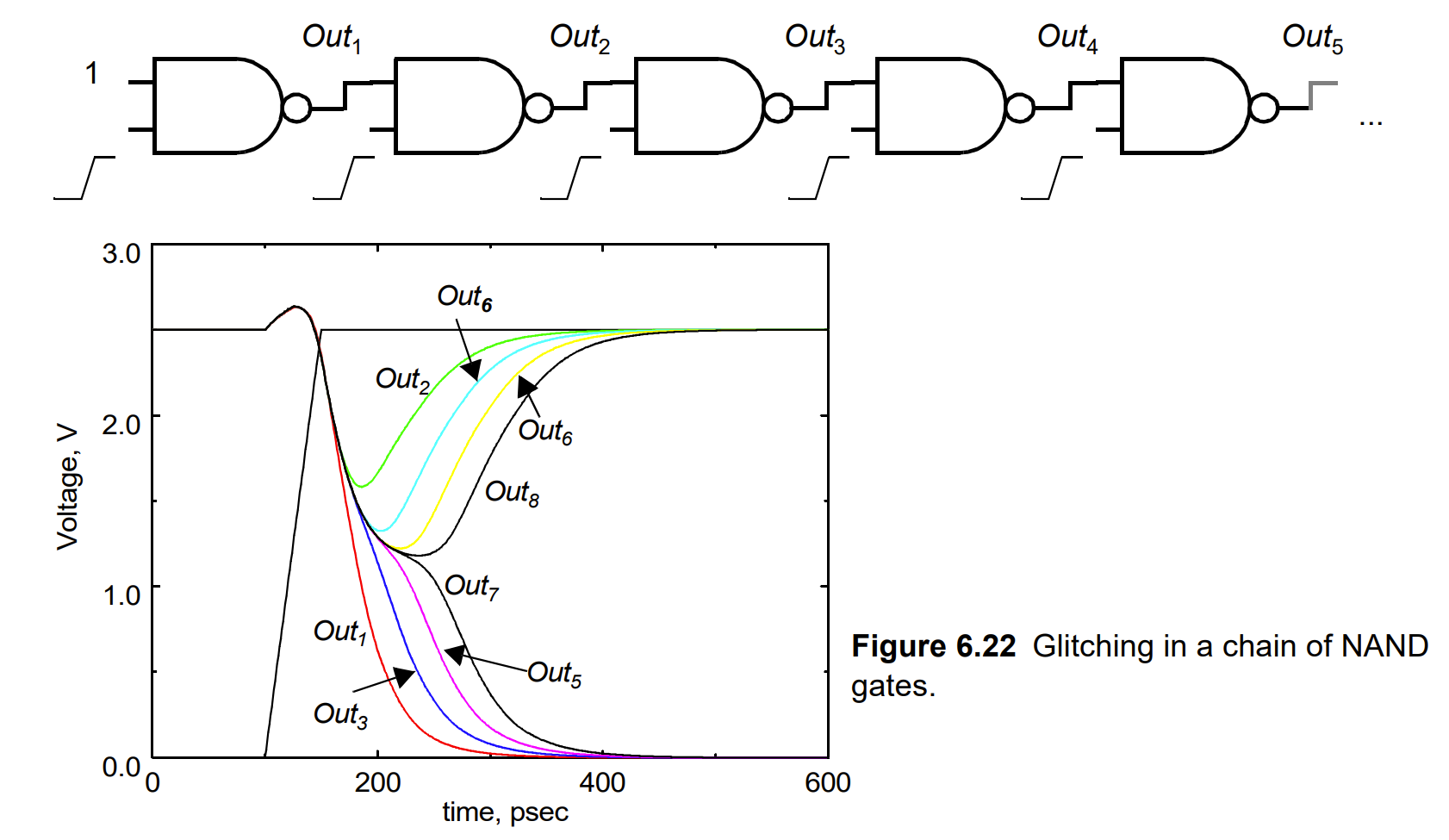
毛刺是指在输出信号中临时的、非预期的电压波动。这种现象通常是由门级别的逻辑变化造成的,因为不同的输入可能以不同的速度到达逻辑门,从而导致短暂的错误状态。
缓解毛刺:
- 使用树形结构
- 或门级联,输入为1概率越大越排前面;与门级联,输入为1概率越小越排前面
- 根据信号到达时间调整顺序
- 把输出或者电源关闭
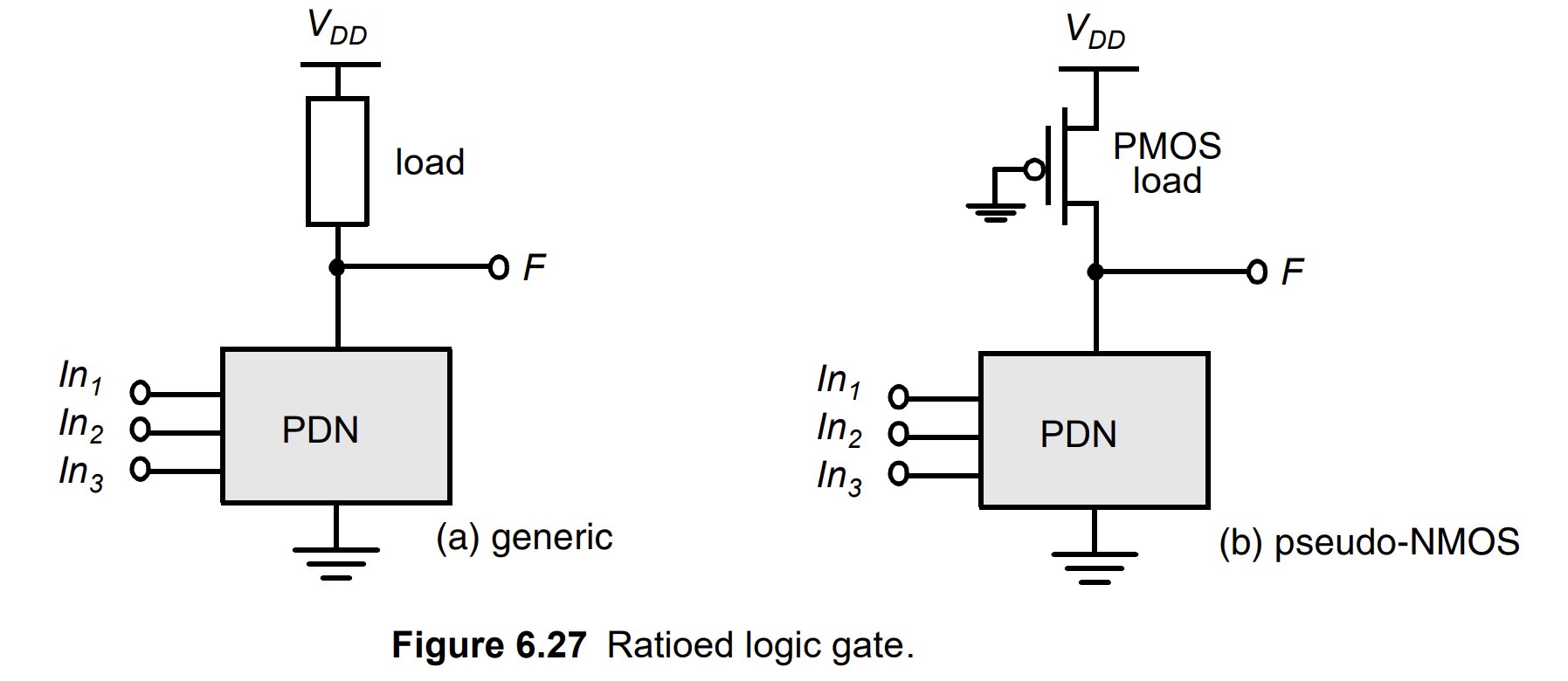
有比逻辑电路
- 有比逻辑试图减少实现特定逻辑功能所需的晶体管数量,但代价是降低鲁棒性和额外功耗。
- 在有比逻辑中,整个 PUN 被一个无条件负载器件取代,该器件将输出拉高以获得高输出。这种栅极由一个实现逻辑功能的 NMOS 下拉网络和一个简单的负载器件组成,而不是有源下拉和上拉网络的组合。右下图显示了一个比率逻辑示例,它使用接地 PMOS 负载,被称为伪 NMOS 栅极。
- 扇入 N,只需要 N+1 个晶体管
- 输入只连接到一个晶体管栅极,电容小
- 不适合大规模电路
- 只适合高速电路
- 只适合大多数时候输出 1 的情况
- 特别适用于 NOR 门
- 总是希望在不工作时关闭 PMOS
工作状态分析
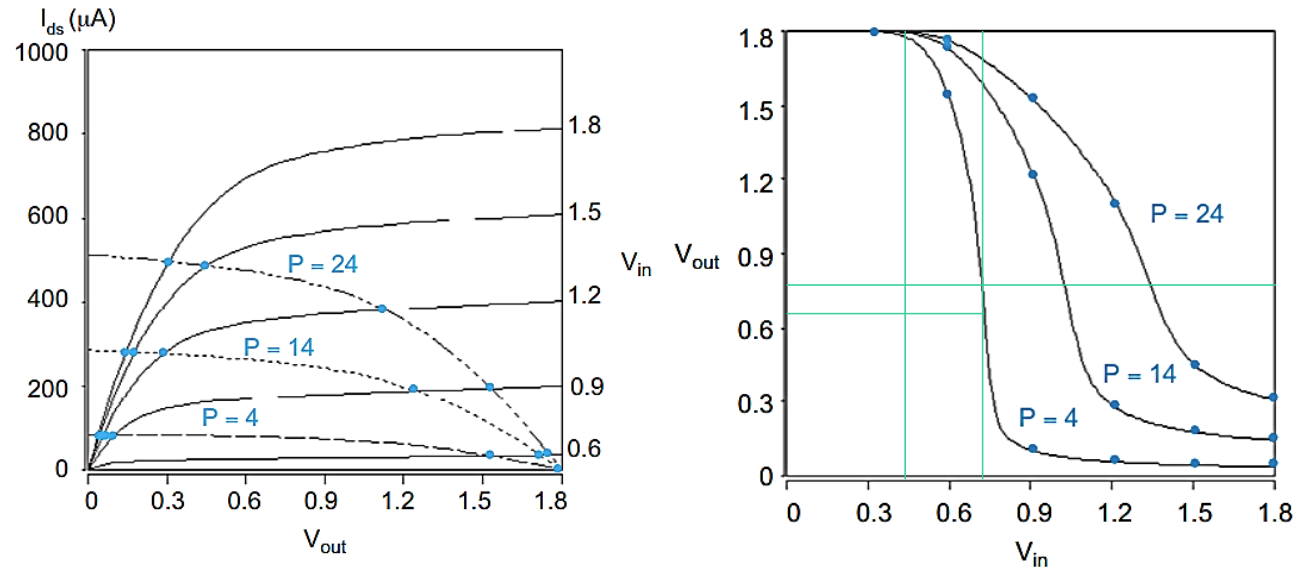
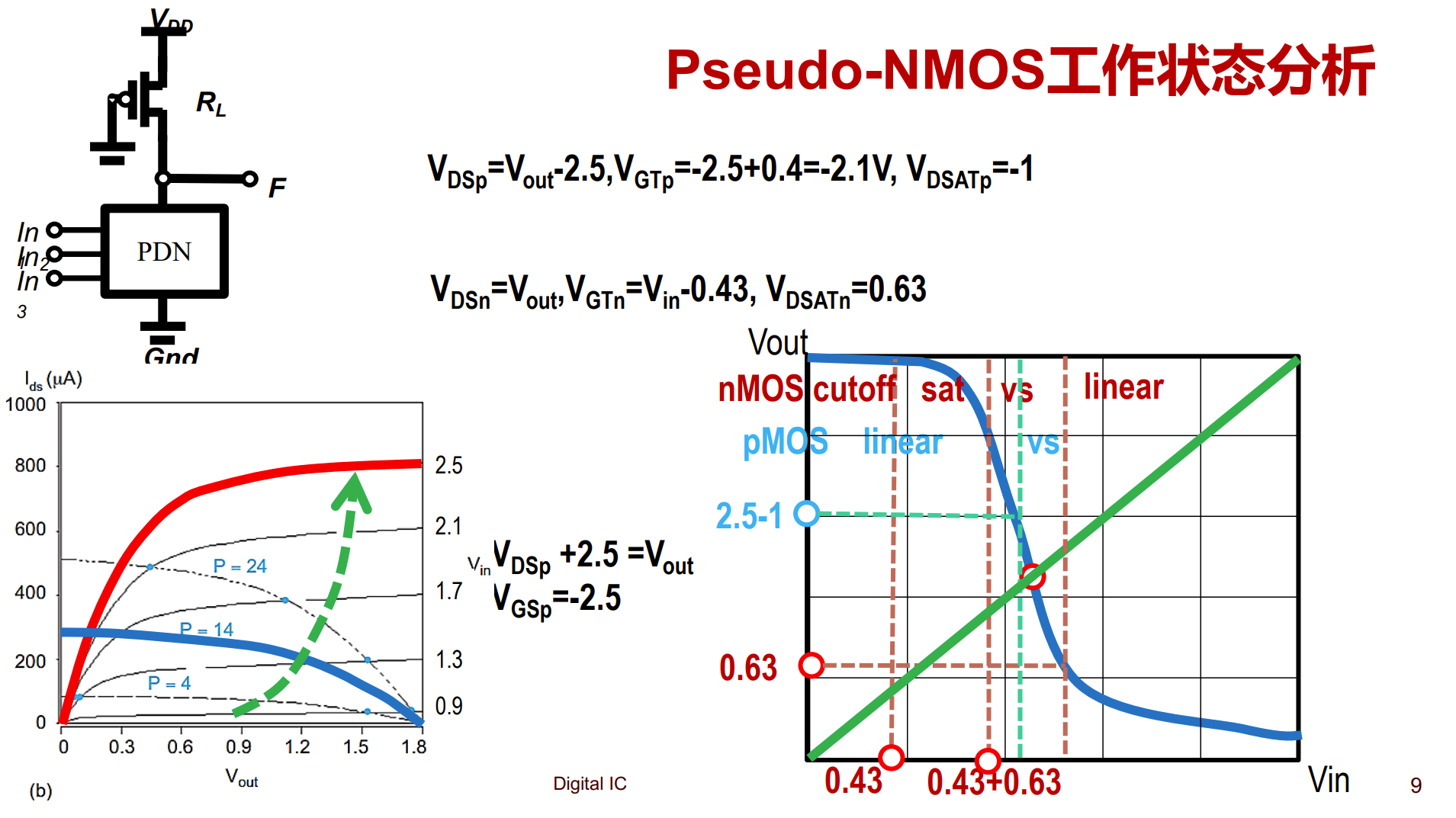
- pMOS 只有线性和速度饱和
- PMOS 尺寸越大($\beta$ 越大),VOL越大,电路静态功耗越大,但是速度越快
逻辑努力推导
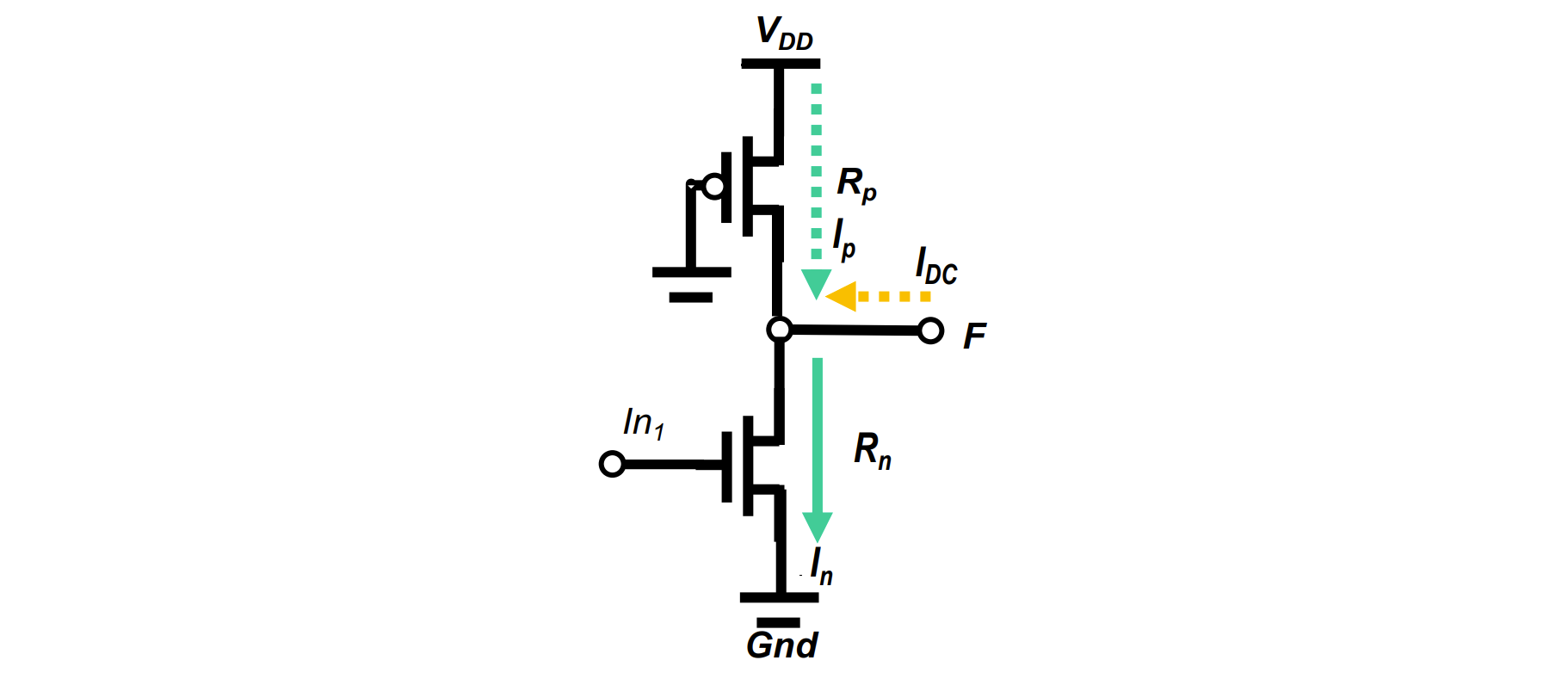
- 尺寸比定为 1:2
- 设单位 NMOS 和单位 PMOS 的电流是 $I_{n0}$ 和 $I_{p0}$,则 $I_{n0}=2I_{p0}$
- 放电电流对齐时因此放电逻辑努力
- 充电电流对齐时因此充电逻辑努力
对于 N 输入 NOR 门,电路延时:
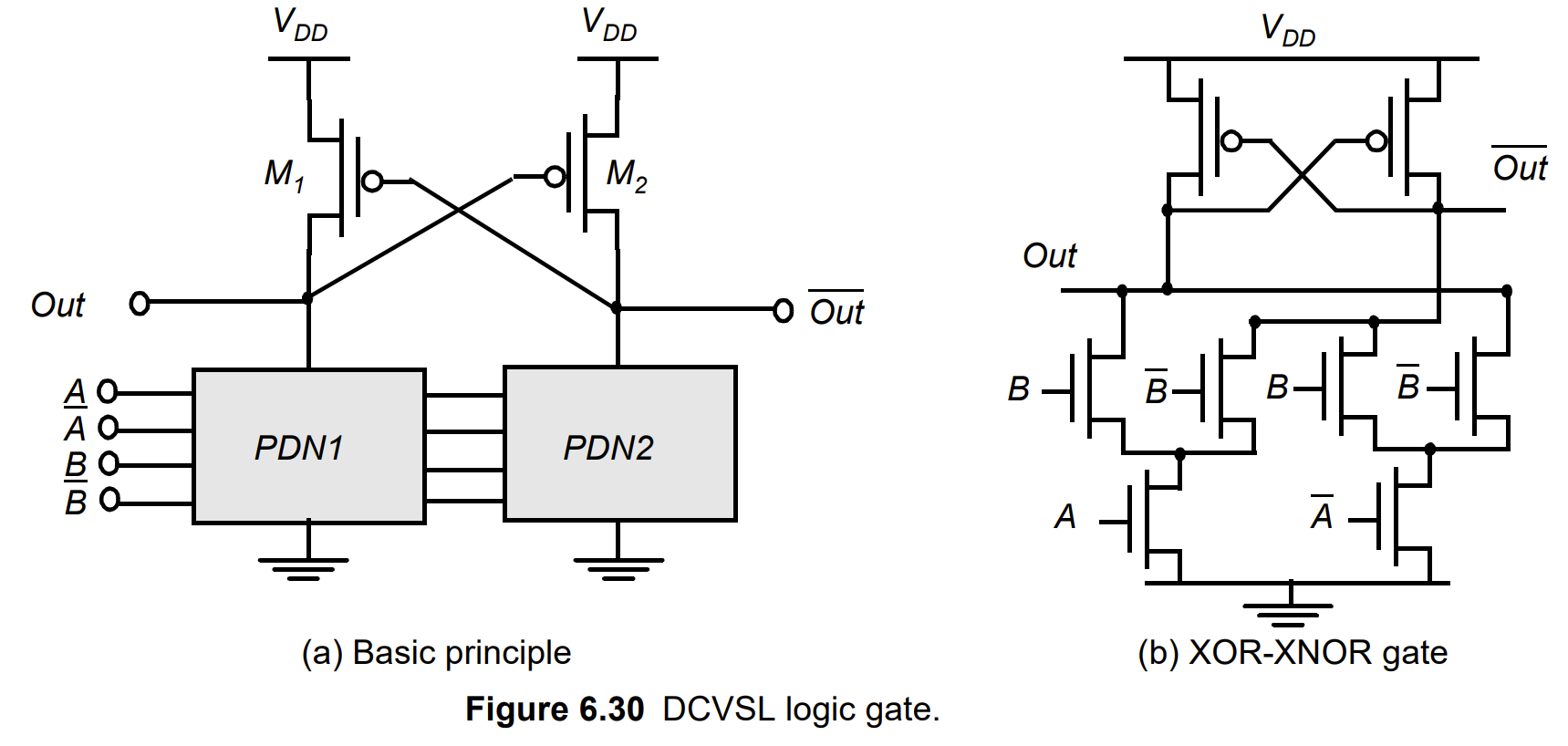
差分串联电压开关逻辑(DCVSL)
传输管逻辑
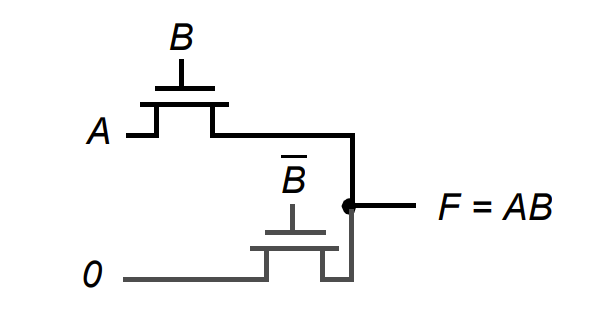
- 与前面提到的一致,NMOS 传递“强0弱1”,PMOS传递“强1弱0”
- Output of passing-transistor should not be connected with the gate of next stage
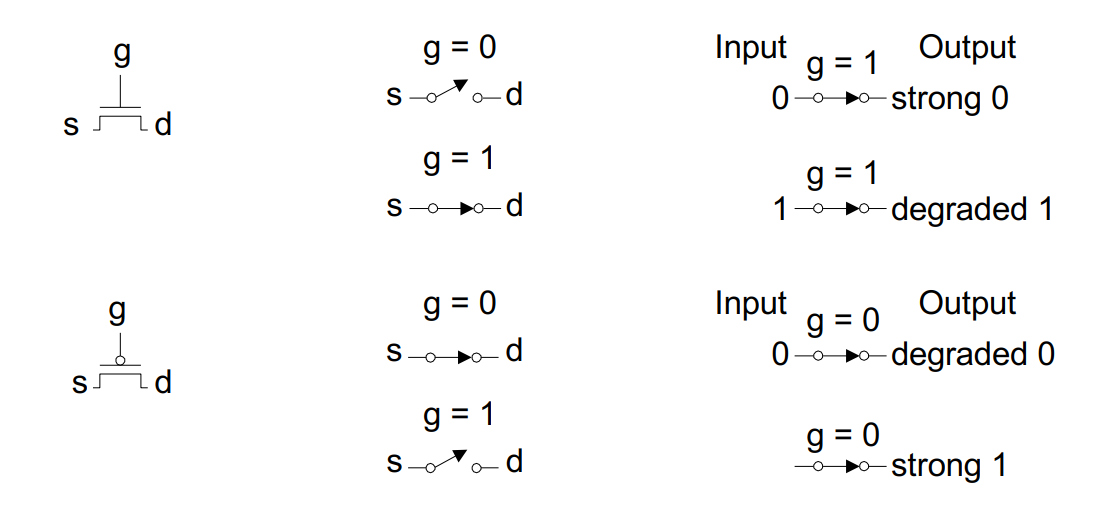
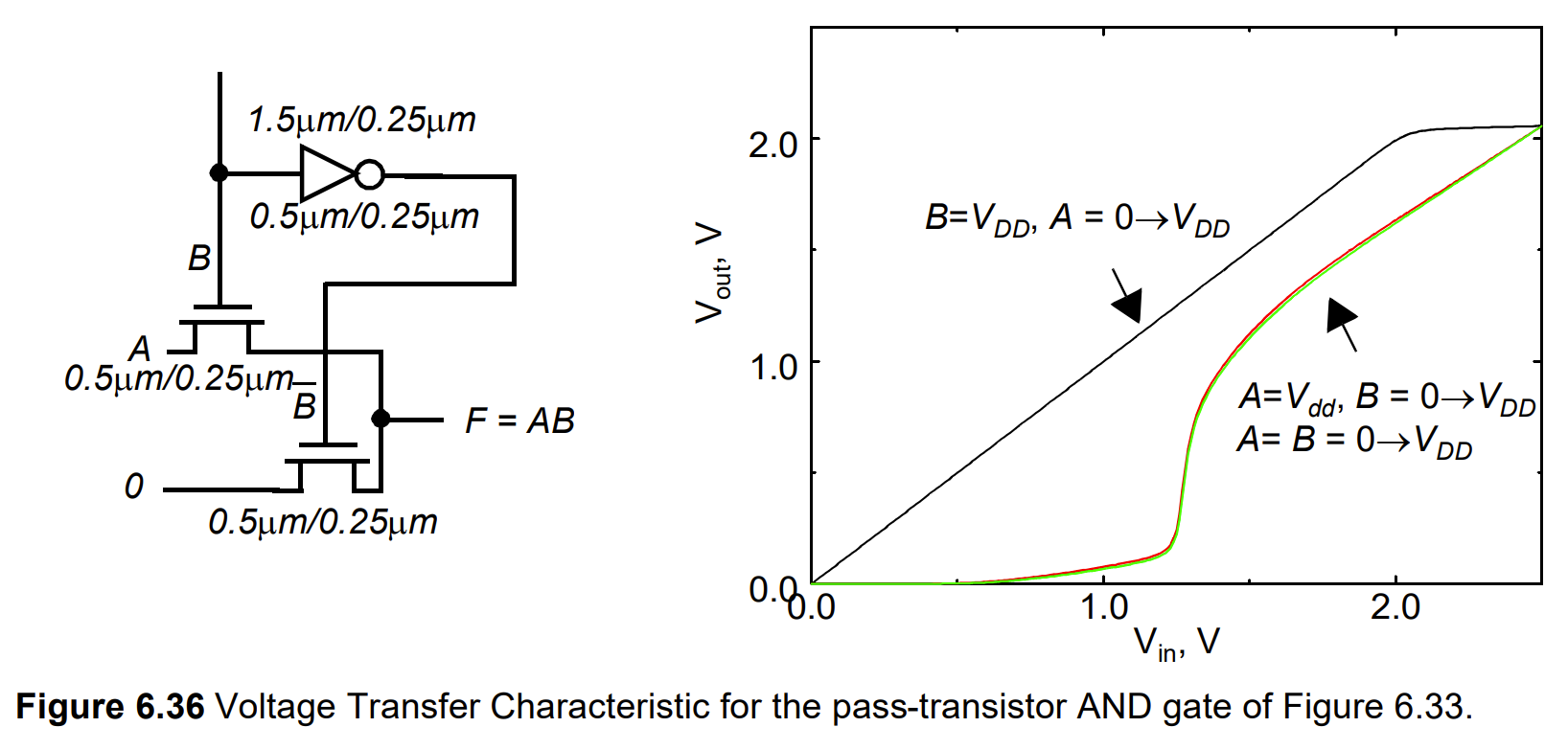
VTC 特性
差分传输管逻辑(CPL)
常用三种门的CPL: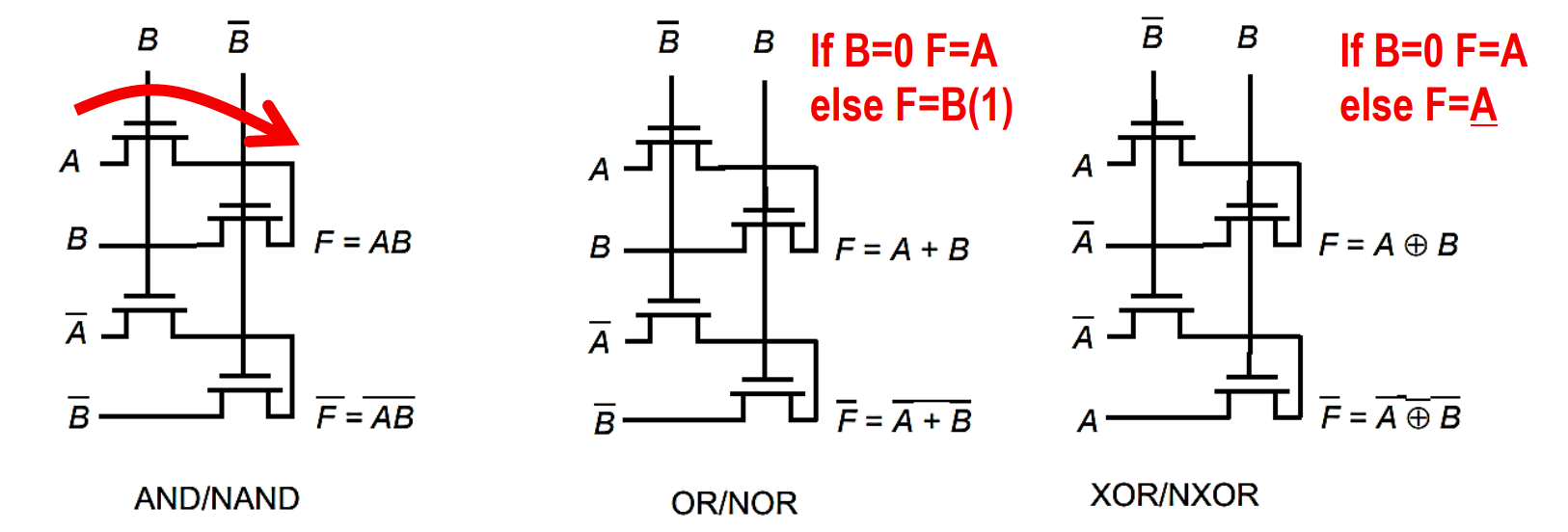
本质其实是选择器
- 诸如XOR和加法器之类的一些门可以用少量晶体管有效地实现。每个信号的两个极性的可用性消除了对额外反相器的需要
- 属于静态门,具有抗噪优势
- 设计非常模块化。实际上,所有门电路都使用完全相同的拓扑结构。这使得门阵列的设计变得简单。通过级联标准模块,可以构建更复杂的门。
电平恢复
方法一:引入反馈回路:
- 该电路的优点是所有电压电平均为 GND 或 VDD,不消耗静态功率
- $M_r$ 的尺寸如果不合适,电路输出不了 0
- 添加电平恢复器会增加内部节点 X 的电容,从而减慢栅极的速度
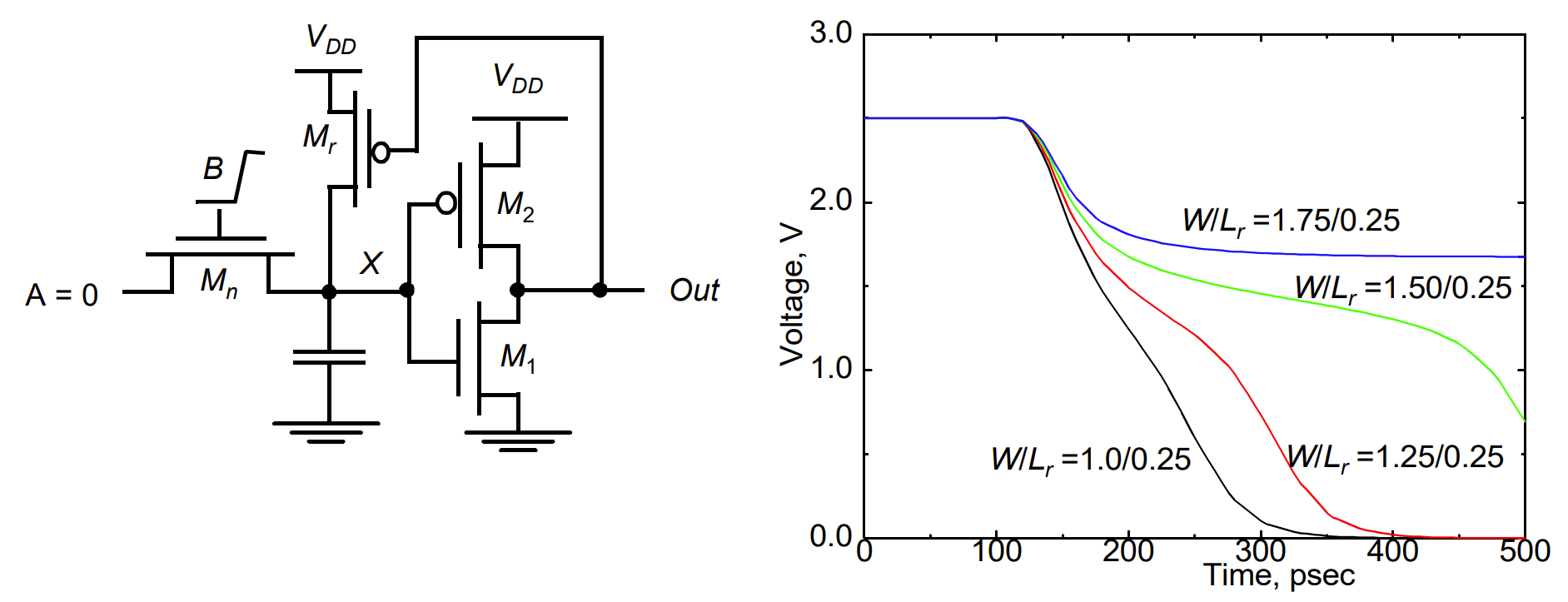
方法二:零或低阈值晶体管
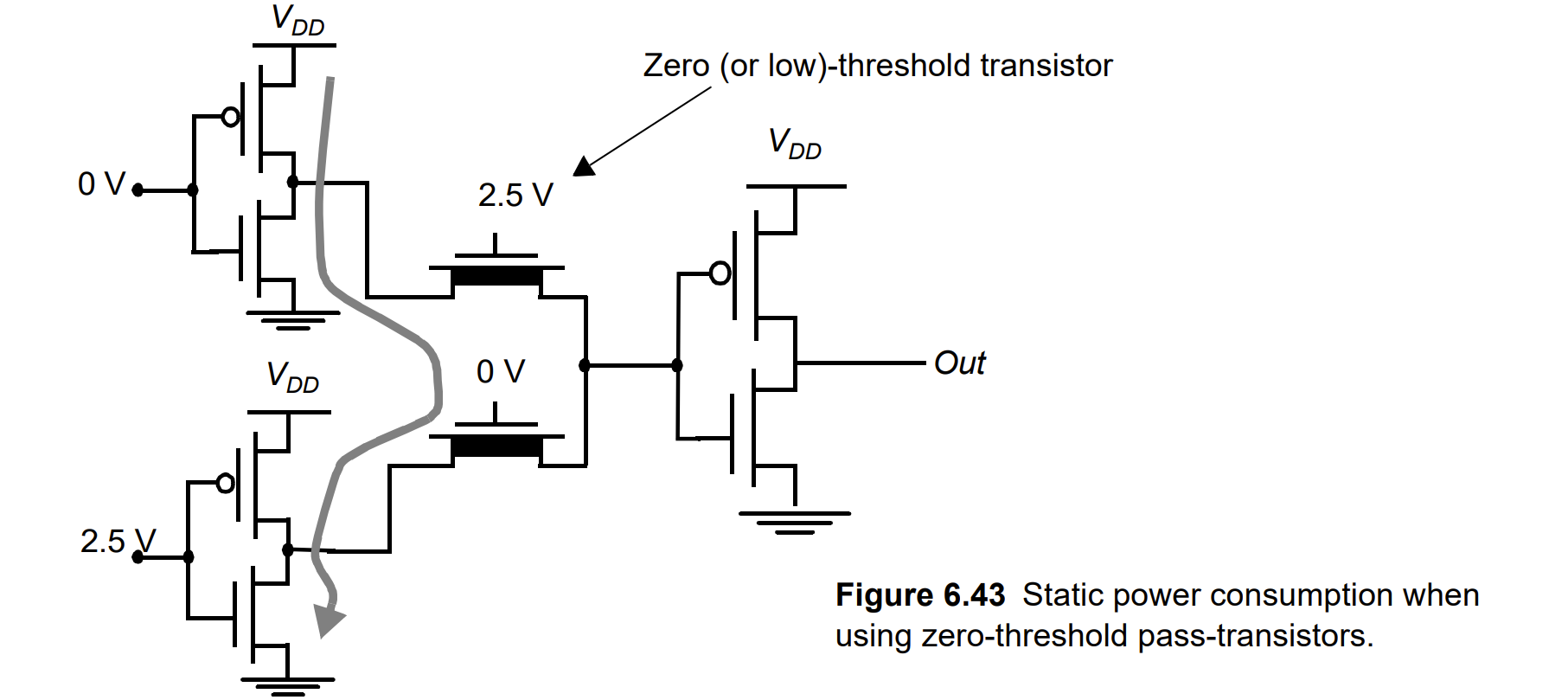
- 由于体偏效应,不可能完全传输强1
- 由于亚阈值电路,可能有潜在的漏直流电通路
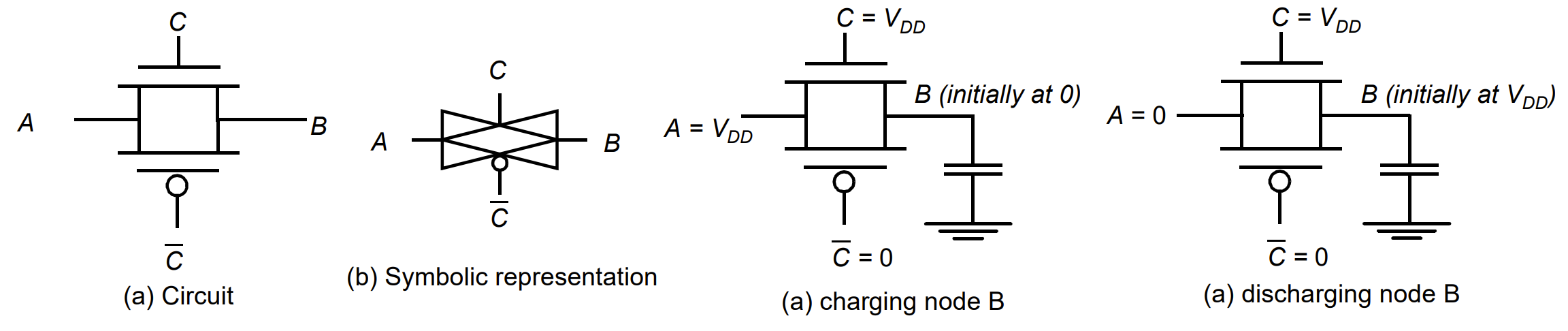
传输门
传输门相当于开关,当 $C=0$ 时高阻,当 $C=1$ 时输出跟随输入
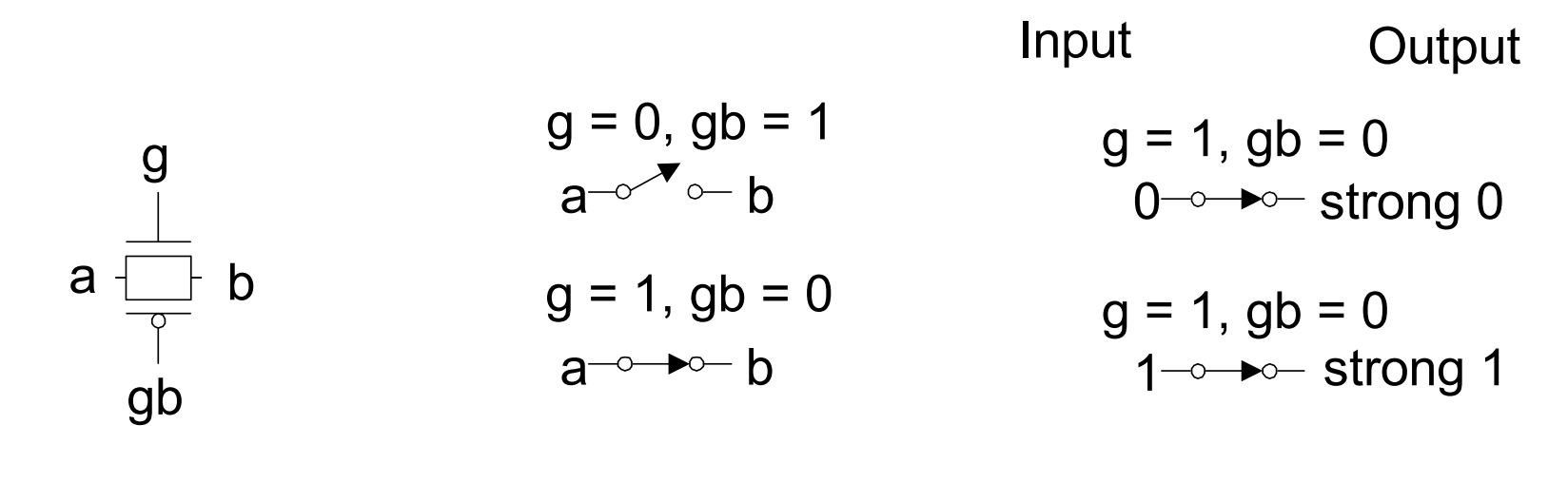
传输门实现异或: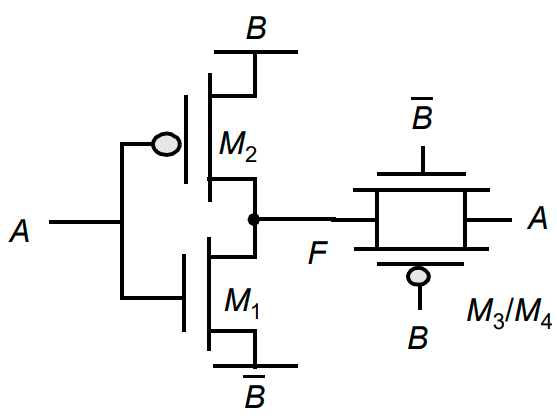
MOS工作状态分析
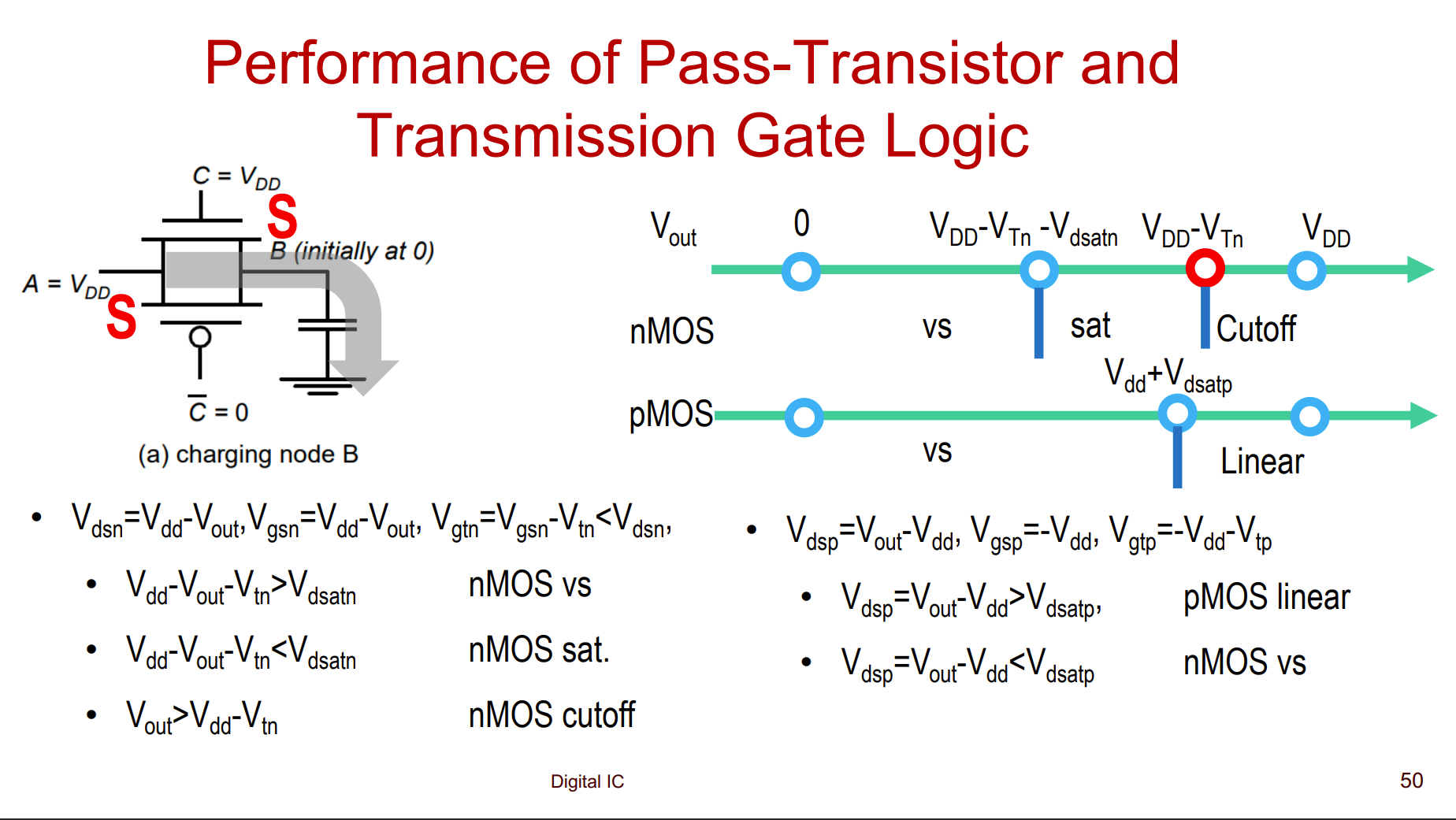
等效电阻
级联优化
(Todo)
动态电路
- 静态电路在每个时间点(开关时除外)的输出都通过低阻抗路径连接到 GND 或 VDD。
- 动态电路则依靠高阻抗节点的电容临时存储信号值。
- 晶体管更少
- 负载电容小
- 延迟小
- 噪声容限不对称($NM_L<NM_H$)
基本组成
在 CMOS PDN 的两端接上一个 NMOS 和一个 PMOS 得到基本动态电路。
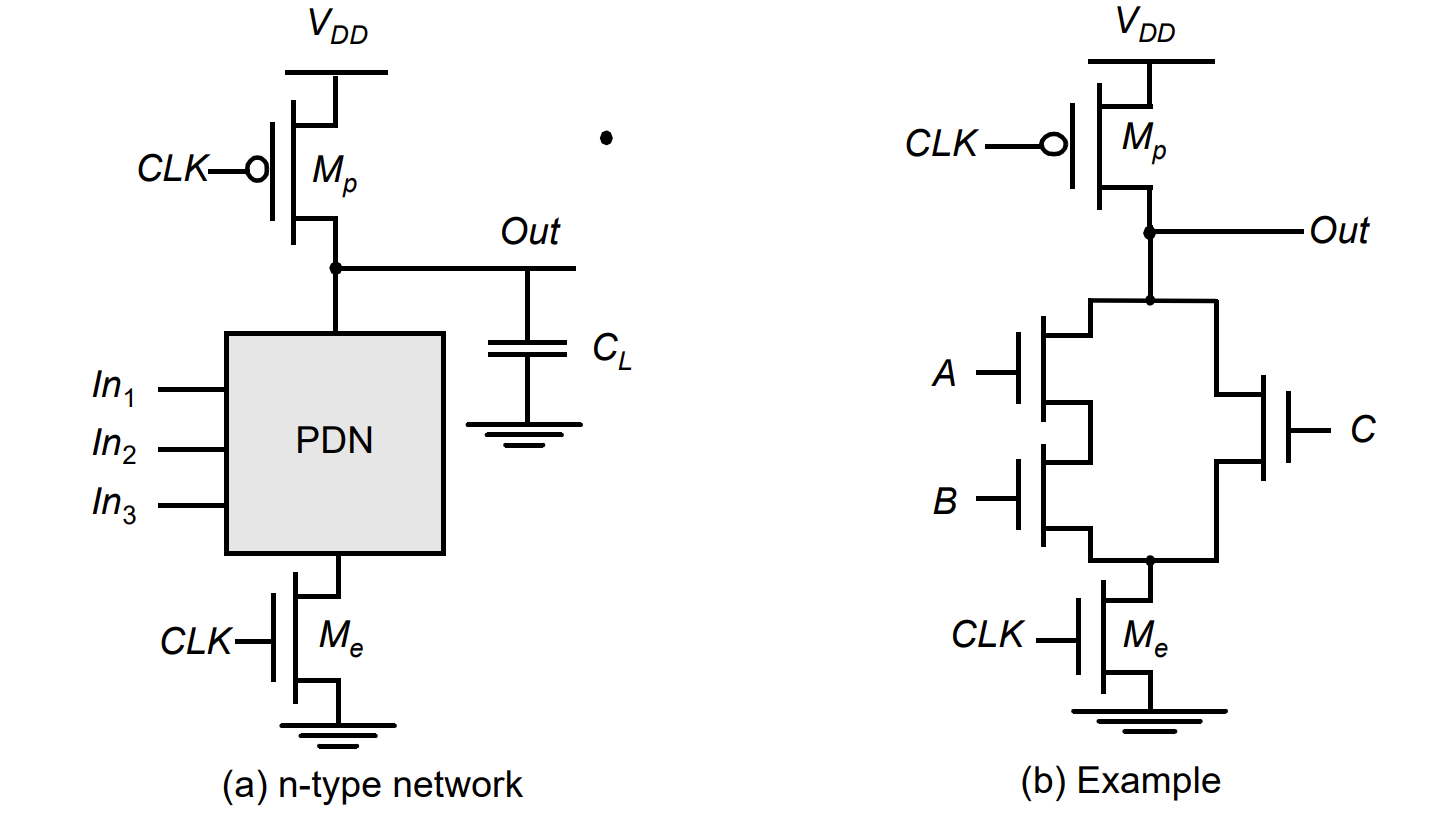
- Precharge:当 CLK=0 时,输出节点 Out 通过 PMOS 晶体管 Mp 被预充电到 VDD。在此期间,评估 NMOS 晶体管 Me 关断,使得下拉路径被禁用,没有静态功率
- Evaluation:当 CLK = 1 时,预充电晶体管 Mp 关断,评估晶体管 Me 接通。输出根据输入值和 PDN 有条件放电。
- 如果输入使 PDN 导通,则输出和接地之间存在低阻路径,输出将放电至接地。
- 如果输入使 PDN 关断,则预充电值仍存储在输出电容 CL 上,该电容由结电容、布线电容和扇出栅极的输入电容组合而成。
- 在评估阶段,输出节点与电源轨之间的唯一可能路径是接地。因此,输出一旦放电,在下一次预充电操作之前就无法再充电。因此,在评估期间,栅极的输入最多只能进行一次转换。请注意,如果下拉网络关闭,输出在评估期间可能处于高阻抗状态。这种行为与输出端和其中一个电源轨之间始终存在低阻路径的静态对应器件有着本质区别。
- 输入不能是 1 到 0
- 如果能保证预充电的时候 PDN 不通,最下面的 MOS 可以去掉
活跃因子
由于动态电路的充电过程是必然发生的,计算活跃因子时只需计算输出为0的概率即可。
逻辑努力

- 充电PMOS尺寸固定为1
- PDN与单位反相器对齐
增加输出保持
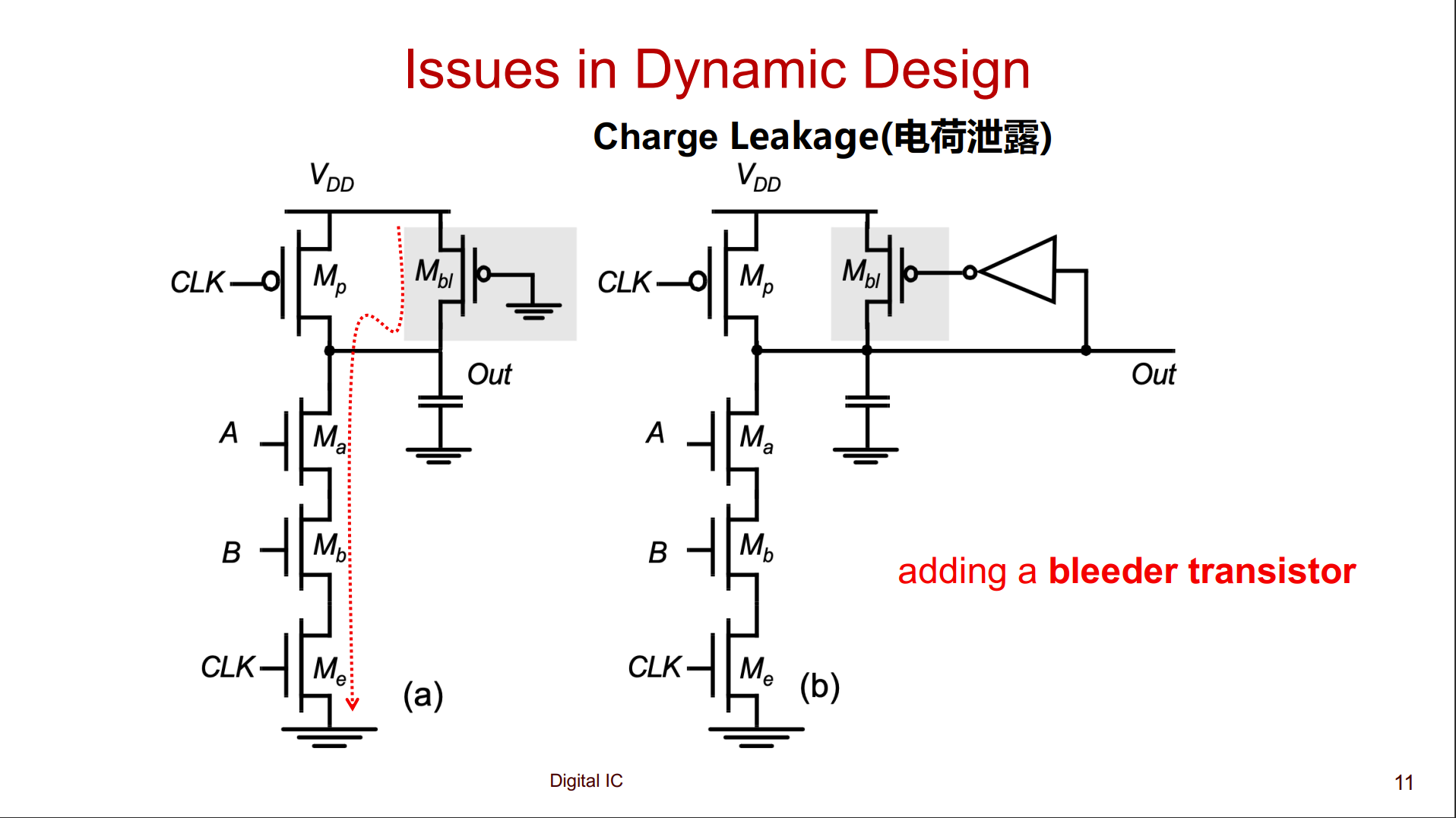
电荷分享(Charge Sharing)
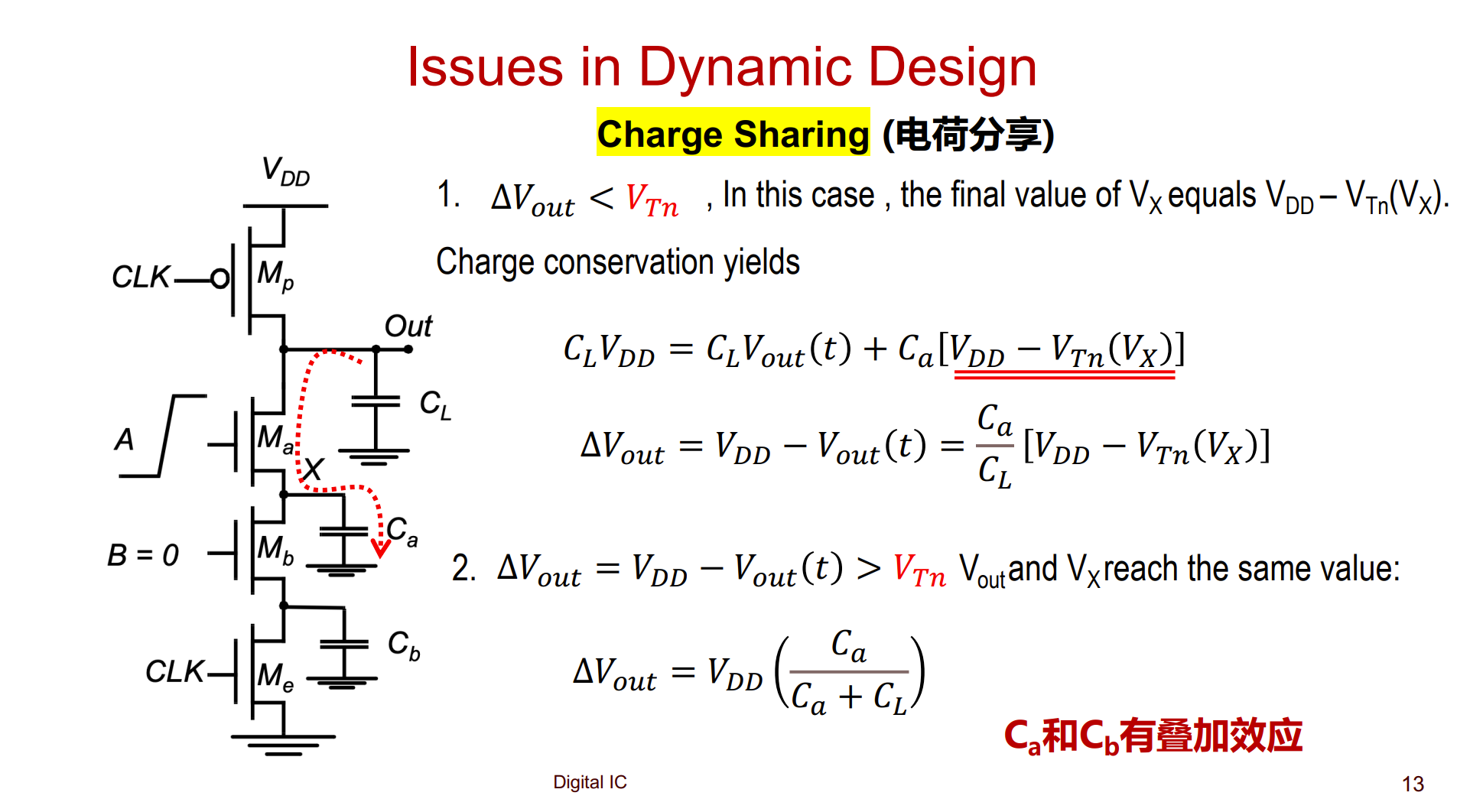
- 当 $\frac{C_L}{C_{a}+C_{L}}>\frac{V_{DD}-V_{Tn}}{V_{DD}}$,则 $C_{a}$ 上的电压会充到 $V_{DD}-V_{Tn}$ 以上,导致 $M_a$ 关闭,最终输出压降为
- 当 $\frac{C_L}{C_{a}+C_{L}}<\frac{V_{DD}-V_{Tn}}{V_{DD}}$,则 $M_a$ 不会关闭,最终 $M_a$ 源漏电压相等,最终输出压降为
时钟馈通与回栅耦合
(GPT)
时钟馈通指的是时钟信号在数字电路中的输入引脚上产生的电压或电流干扰,进而影响到其他的信号线或电路。时钟信号通常用于同步操作,例如触发时序逻辑电路的工作。由于时钟信号在整个电路中广泛传播,它的边沿变化可能会引起瞬态电流或电压变化,这些变化可能通过电路中的电容或电感耦合到其他信号线上,导致不可预测的干扰。时钟馈通可能导致电路中的时序错误,例如时钟抖动、时序抖动、数据误码等问题。
回栅耦合是一种干扰现象,主要发生在场效应晶体管(FET)中。在FET的设计中,栅极(Gate)控制着通道中的电流流动。然而,由于栅极与其他电路元件之间的物理接近,栅极信号可能会通过电容耦合或电感耦合传播到其他部分,干扰其他电路中的信号。特别是在高集成度的集成电路中,晶体管之间的互相干扰变得更为显著。回栅耦合可能导致电路中的失真、功耗增加、噪声增加等问题。
为了减少时钟馈通和回栅耦合的影响,可以采取一些设计和布局上的技术手段。例如,可以通过合理的布线规划和屏蔽来减少时钟馈通。对于回栅耦合,可以使用适当的电源和接地设计,以及合适的电源/接地引脚布局来减少干扰。此外,还可以使用屏蔽层、隔离层和电源/接地格线等技术来隔离电路之间的相互干扰。设计者还可以采用低耦合电路结构、布局优化、电源滤波等技术来降低时钟馈通和回栅耦合的影响。
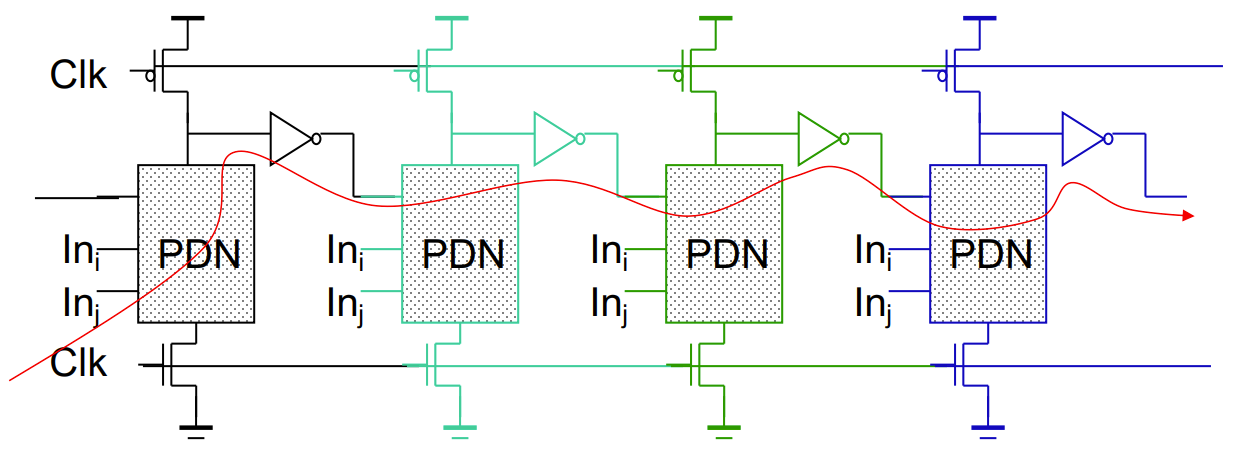
多米诺门
- 若将动态电路反相器直接相连,会出现输入是 1 到 0 的情况,这是不被允许的
- 使用一个动态电路+一个 CMOS 反相器组成一个多米诺门
- 多米诺门链中,非第一级的门,PDN 下面的 NMOS(连接 CLK)可以省略
np-CMOS
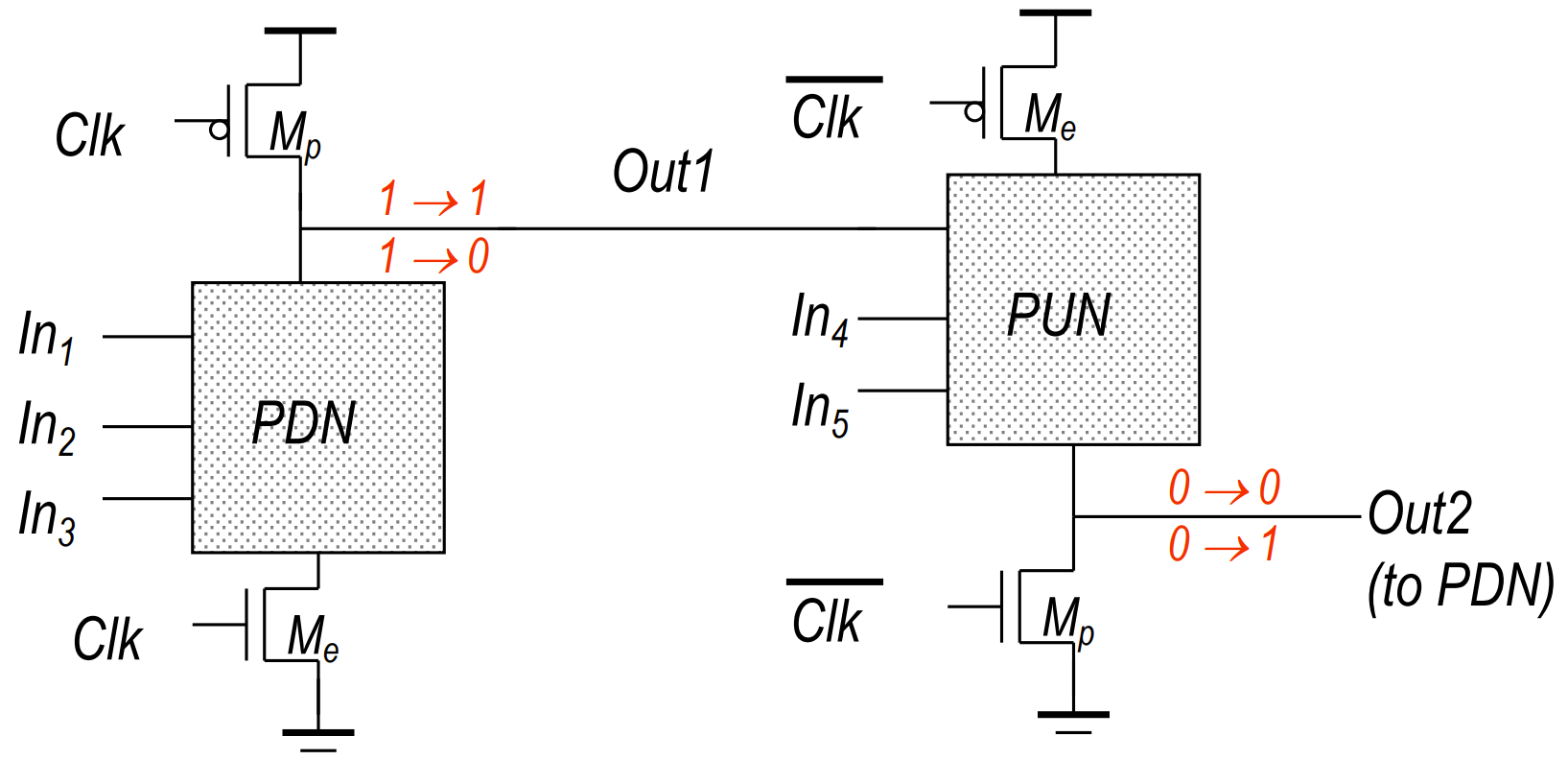
左边电路就是上面提到的动态电路,右边是反过来用PUN做的,所以左边电路输出不可能是 0 到 1,而右边电路输出不可能是 1 到 0
优缺点
- Smaller area(N+2 versus 2N)
- Full swing outputs ($V_{OL} = GND$ and $V_{OH} = VDD$)
- non-ratioed
- only dynamic power(no static current, no $P_{sc}$)
- Faster switching speeds
- reduced load capacitance due to lower input capacitance ($C_{in}$)
- reduced load capacitance due to smaller output loading ($C_{out}$)
1.5-2x faster than static CMOS
Overall power dissipation usually higher than static CMOS
- higher transition probabilities
- PDN starts to work when the input signals exceed $V_{Tn}$
- $V_{M}$, $V_{IH}$ and $V_{IL}$ equal to $V_{Tn}$
- Needs a precharge/evaluate clock
- many challenges: Monotonicity/Leakage/Charge sharing/Noise
第七章 数据通路
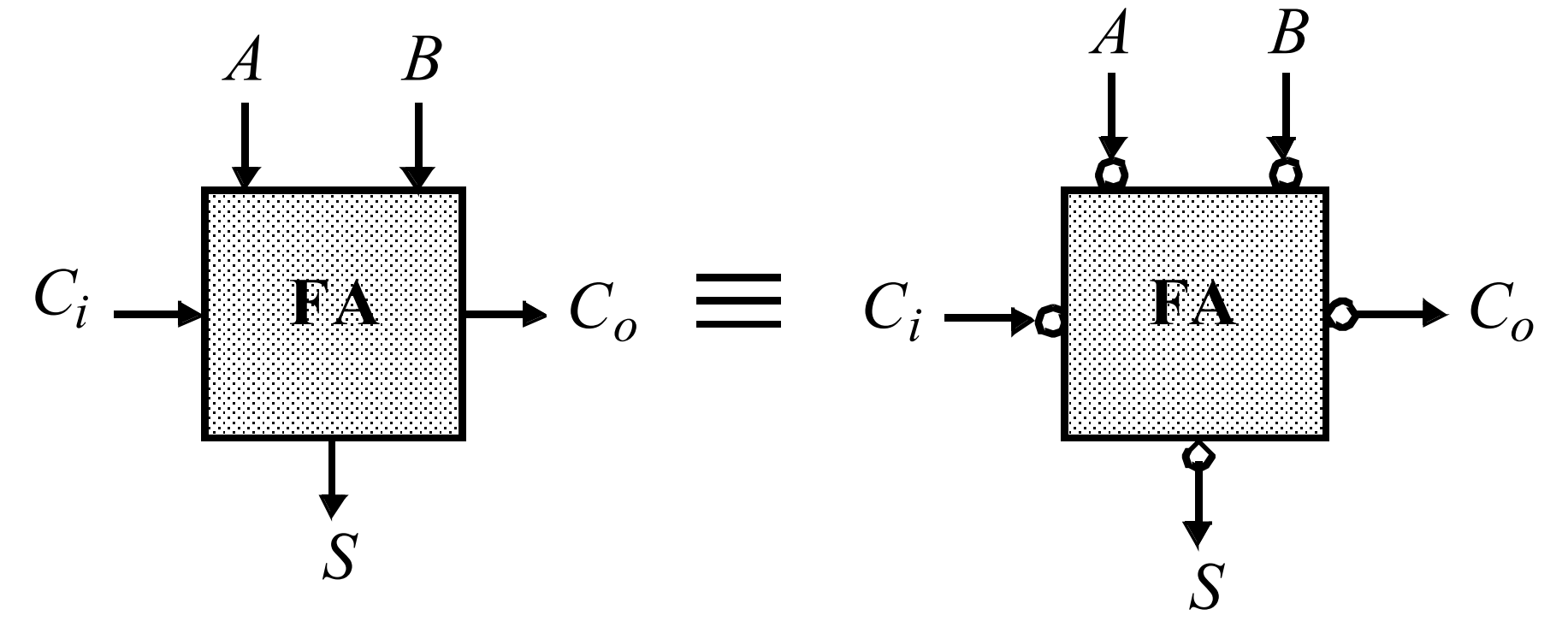
一位加法器
真值表:
因此输出的逻辑表达式:
镜像性
- 将 $A$、$B$、$C_{\mathrm{i}}$ 均取反,输出的 $\mathrm{C}_{\mathrm{o}}$ 和 $S$ 也是取反
Full Adder
28T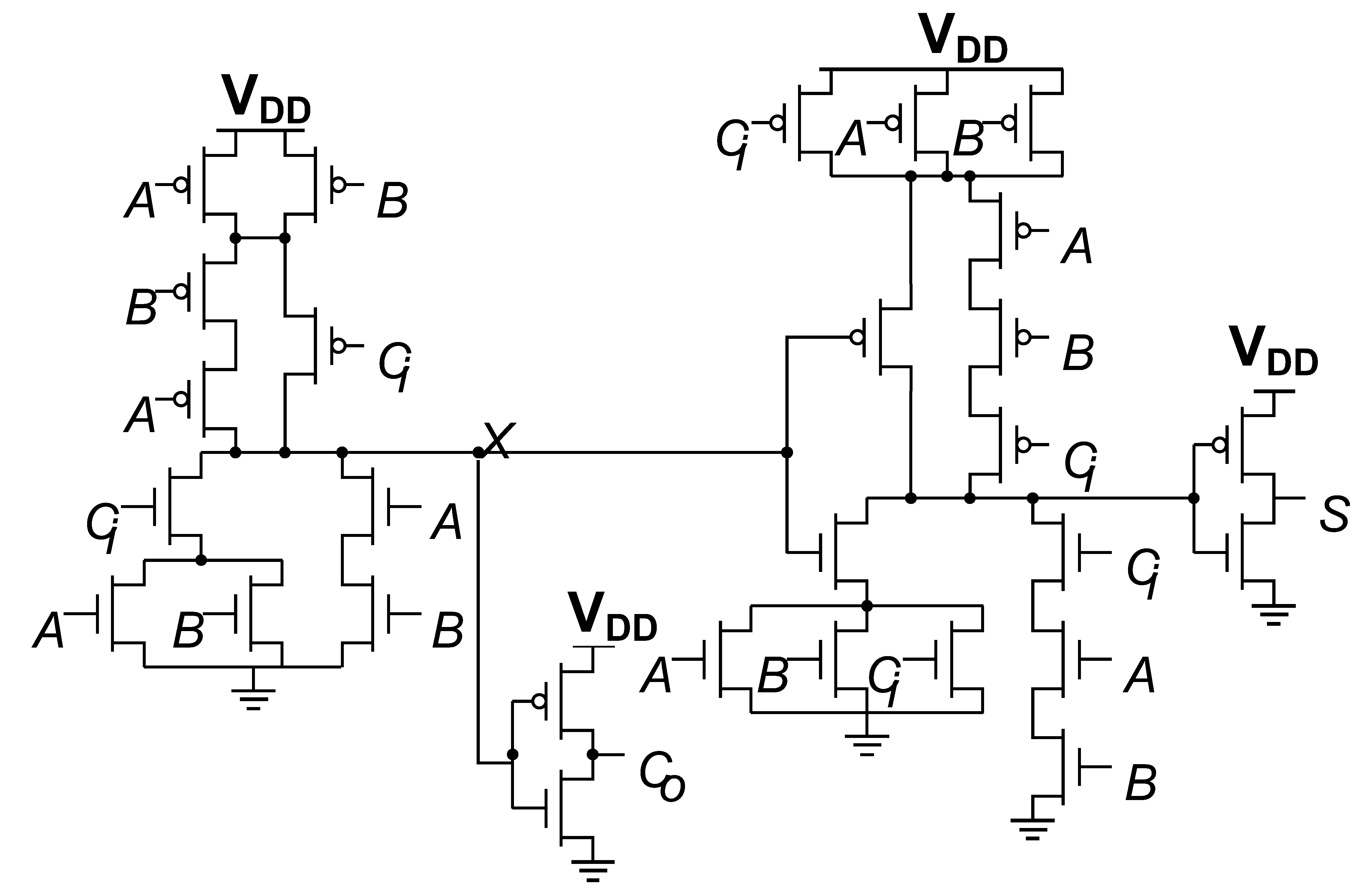
24T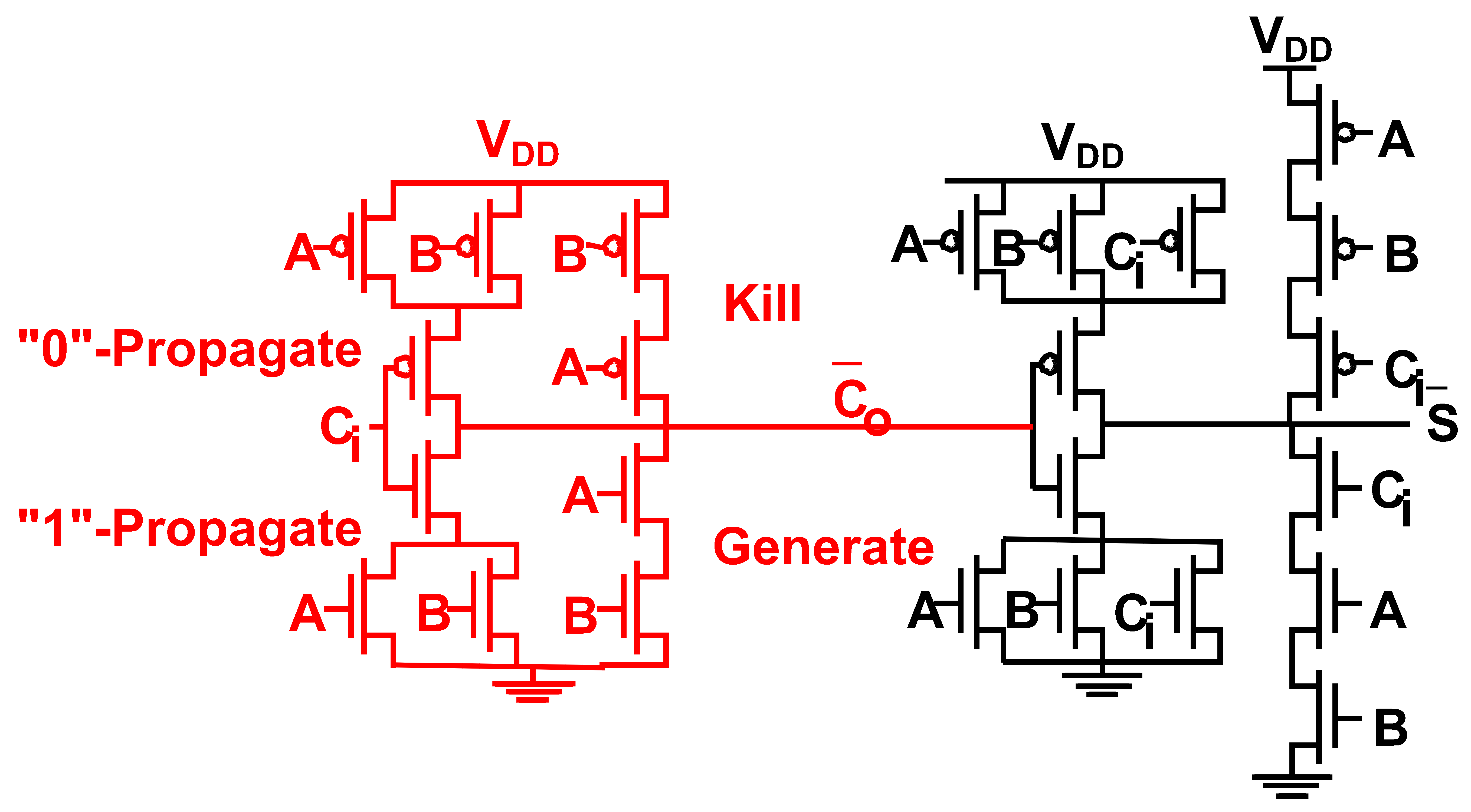
PGK
- 定义两个输入都为 0 时,为消除过程
- $K=\bar{A}\bar{B}$
- 定义两个输入只有一个为 1 时,为传播过程
- $P=A\oplus B$
- 定义两个输入都为 1 时,为产生过程
- $G=AB$
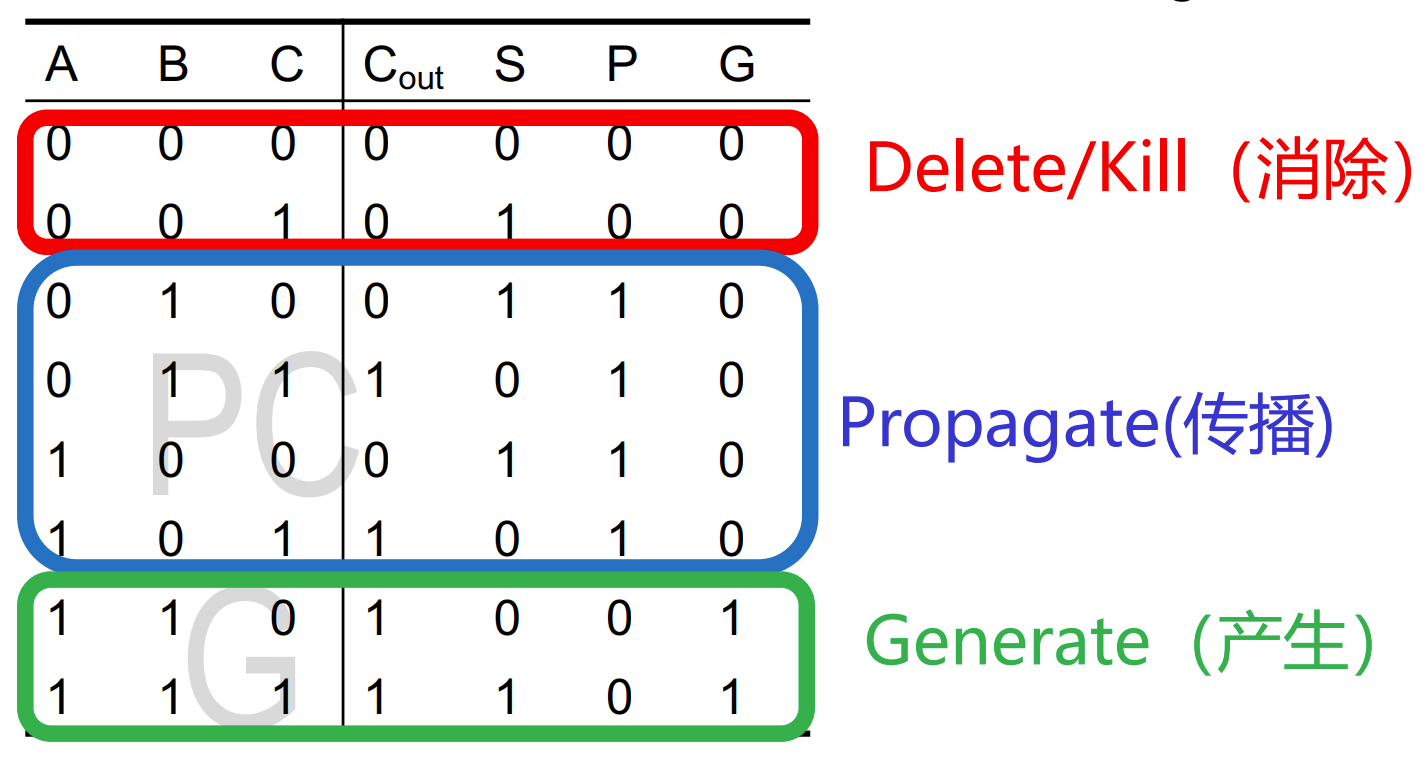
因此,两个输出可以分别写成:
XOR Full Adder
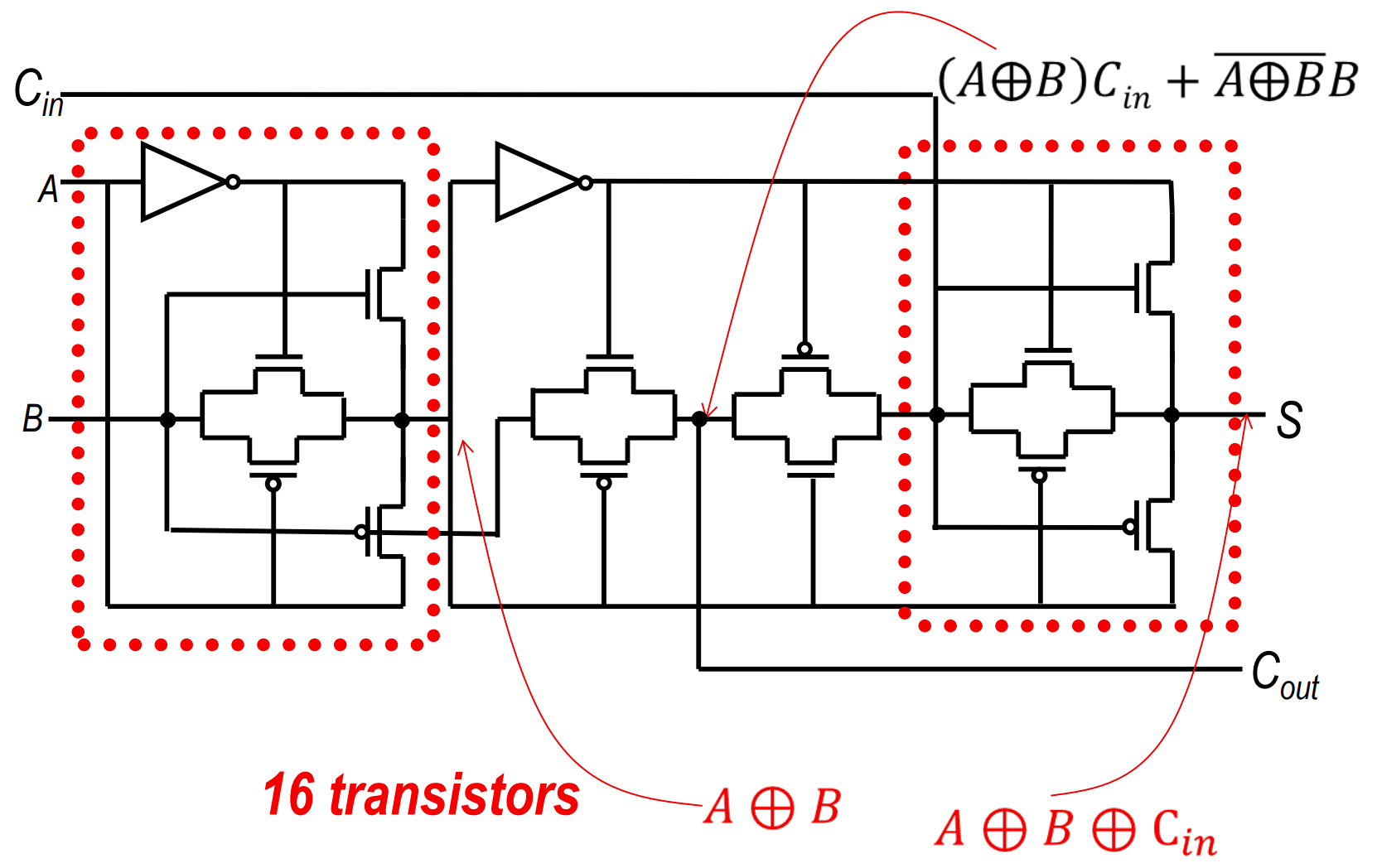
CPL Full Adder
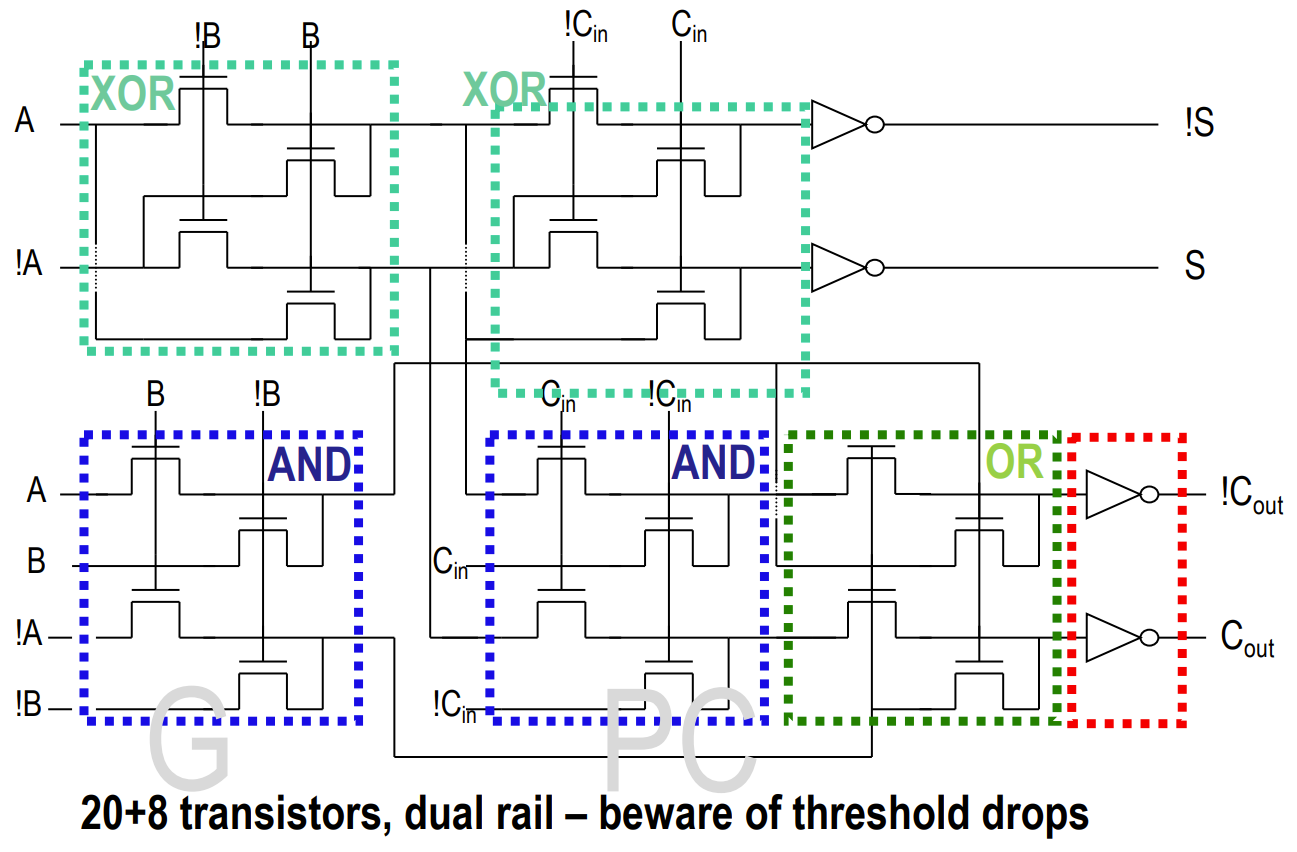
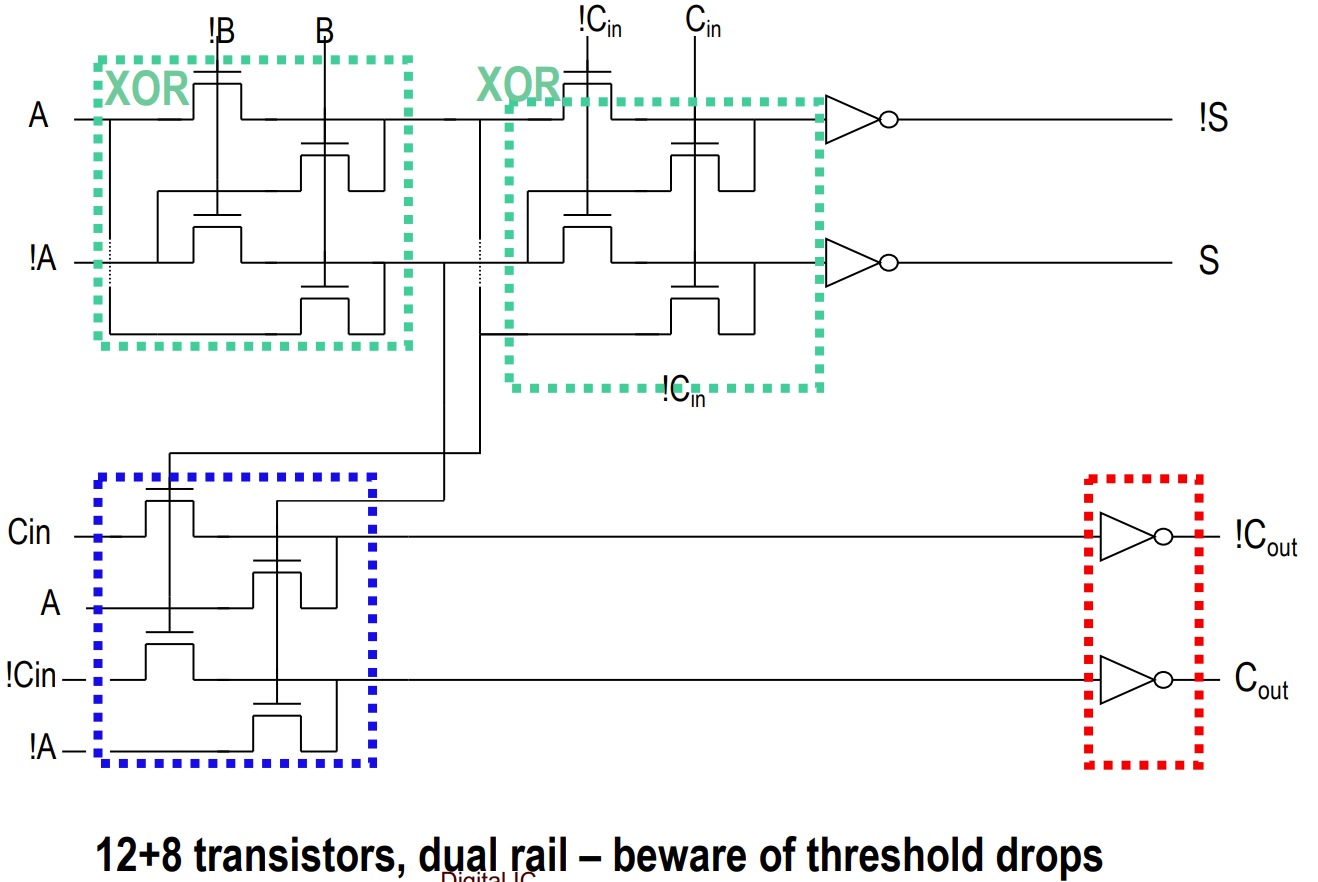
曼彻斯特进位链(Manchester Carry Chain)
由于 PGK(D) 是互斥的,直接把输出接在一起: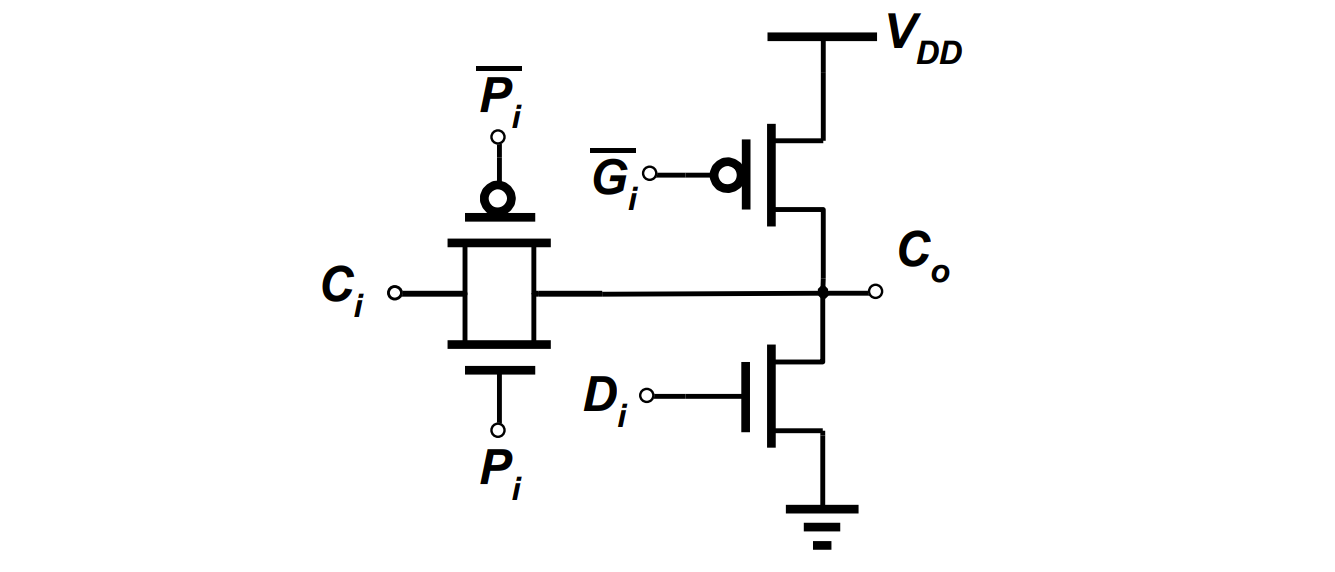
增加预充过程,转换为动态电路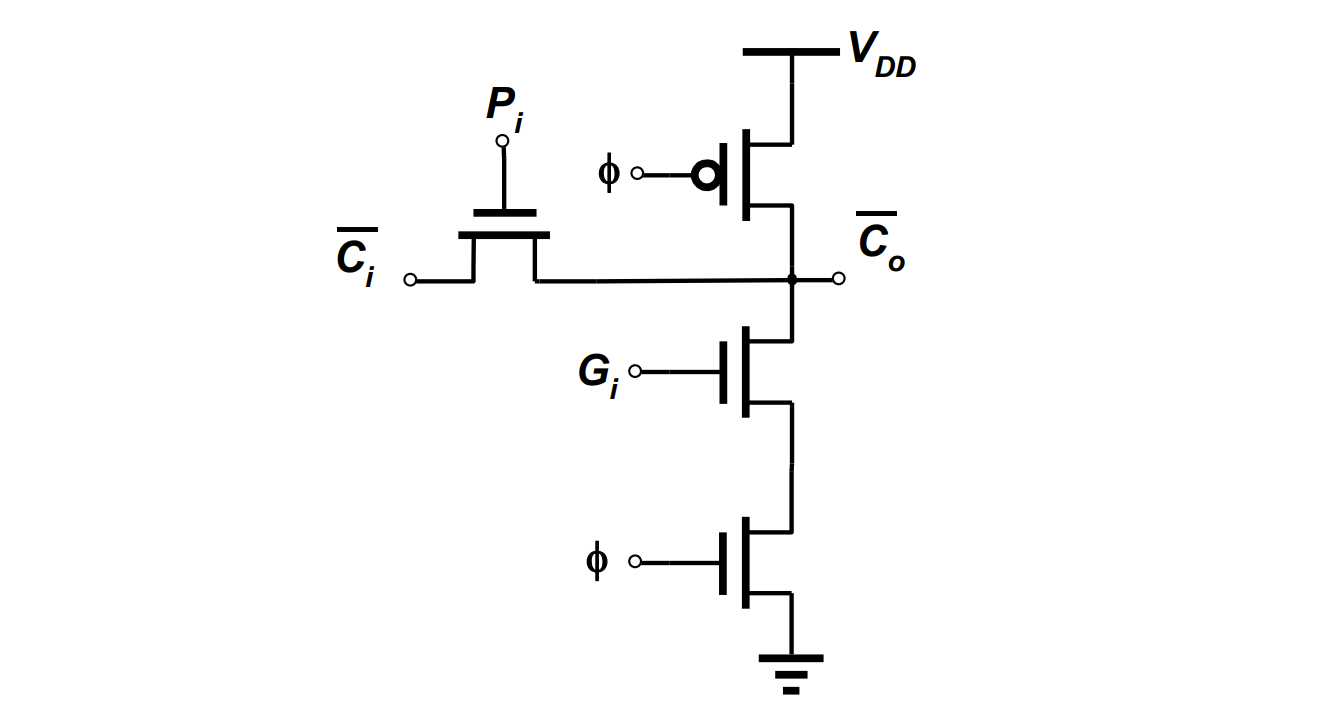
四个级联: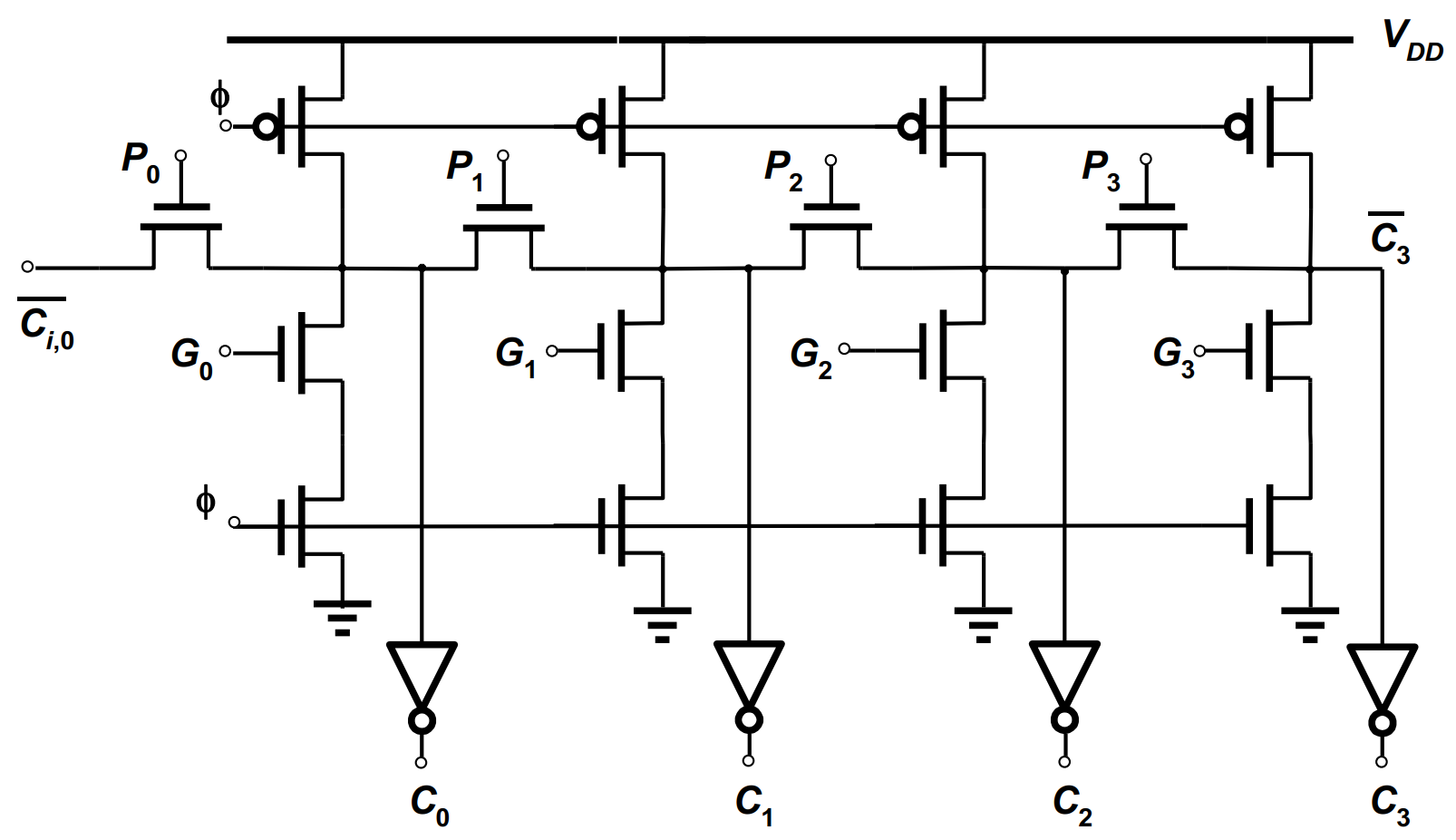
前面提到 $P=A\oplus B$ 可以替换成 $P=A+B$,但是在 MCC 这里不行,会出错。
分组
原因
进位的路径最慢,而前面部分只与对应输入位有关,可以提前计算
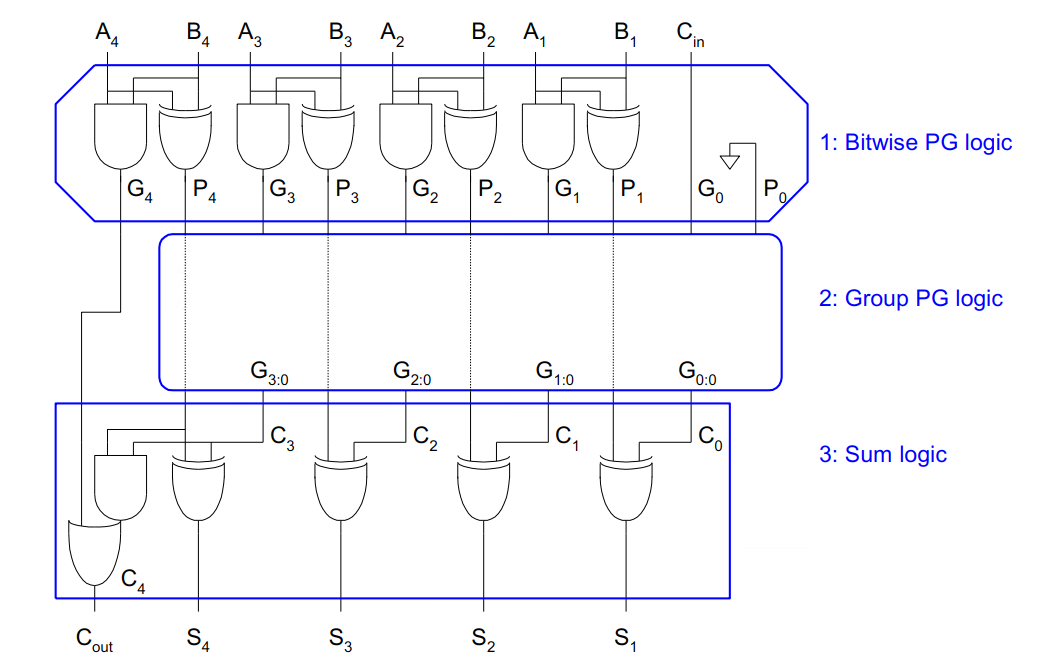
分组GP定义
- 定义 $G_{i,j}$ 和 $P_{i,j}$ 为第 $i$ 位到第 $j$ 位的状态
- 转移方程
- 边界条件(PG 准备层)
- PG 逻辑层目标
- 结果(求和逻辑)
PG 图
基础模板
基本积木
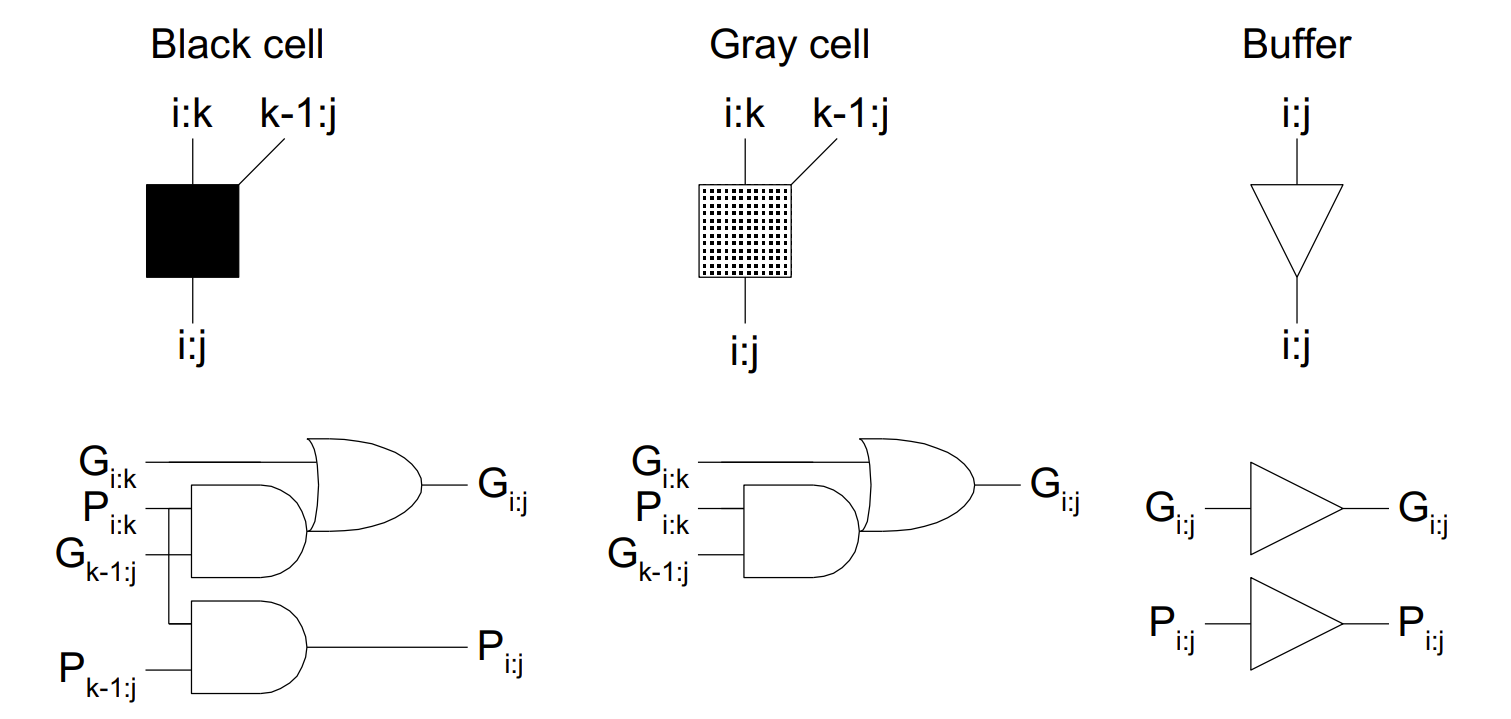
- Black cell 计算 $G_{i:j}$ 和 $P_{i:j}$
- Gray cell 计算 $G_{i:j}$
- Buffer 缓冲
- Black cell 两块输入都需要 PG
- Gray cell 前一块输入需要 PG,后一块只需要 G
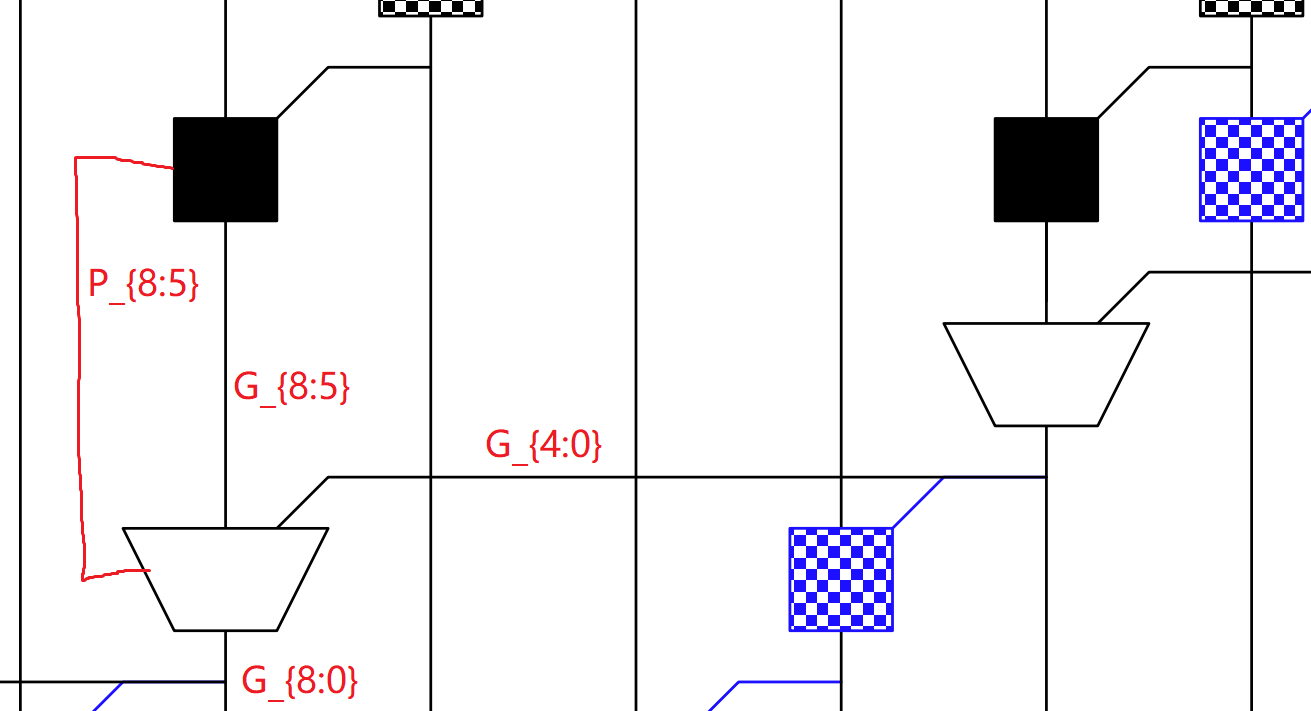
- Black cell 下还可接选择器
Carry-Ripple PG Diagram
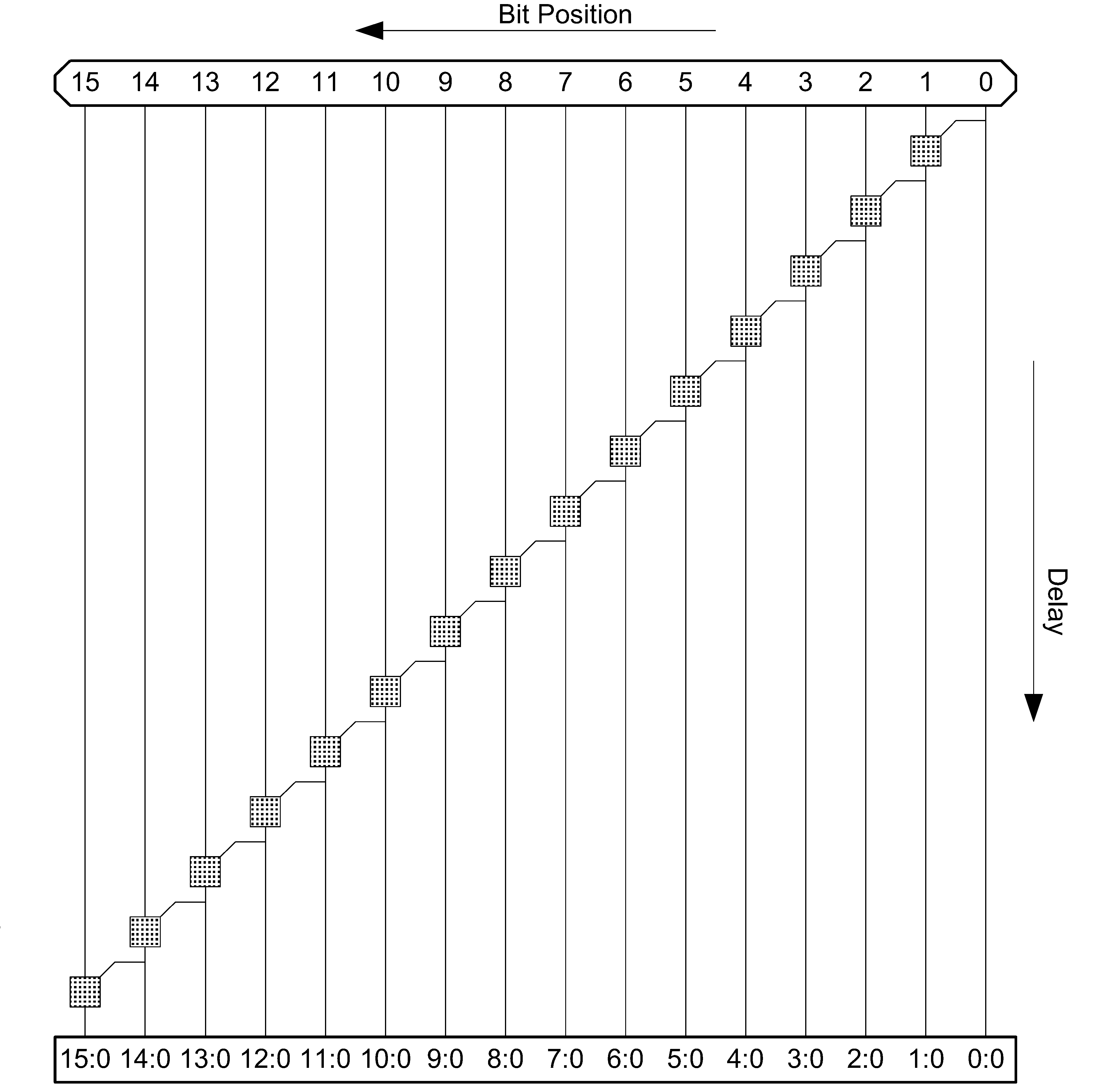
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| N-1 | 2 | 1 | N |
Carry-Skip PG Diagram
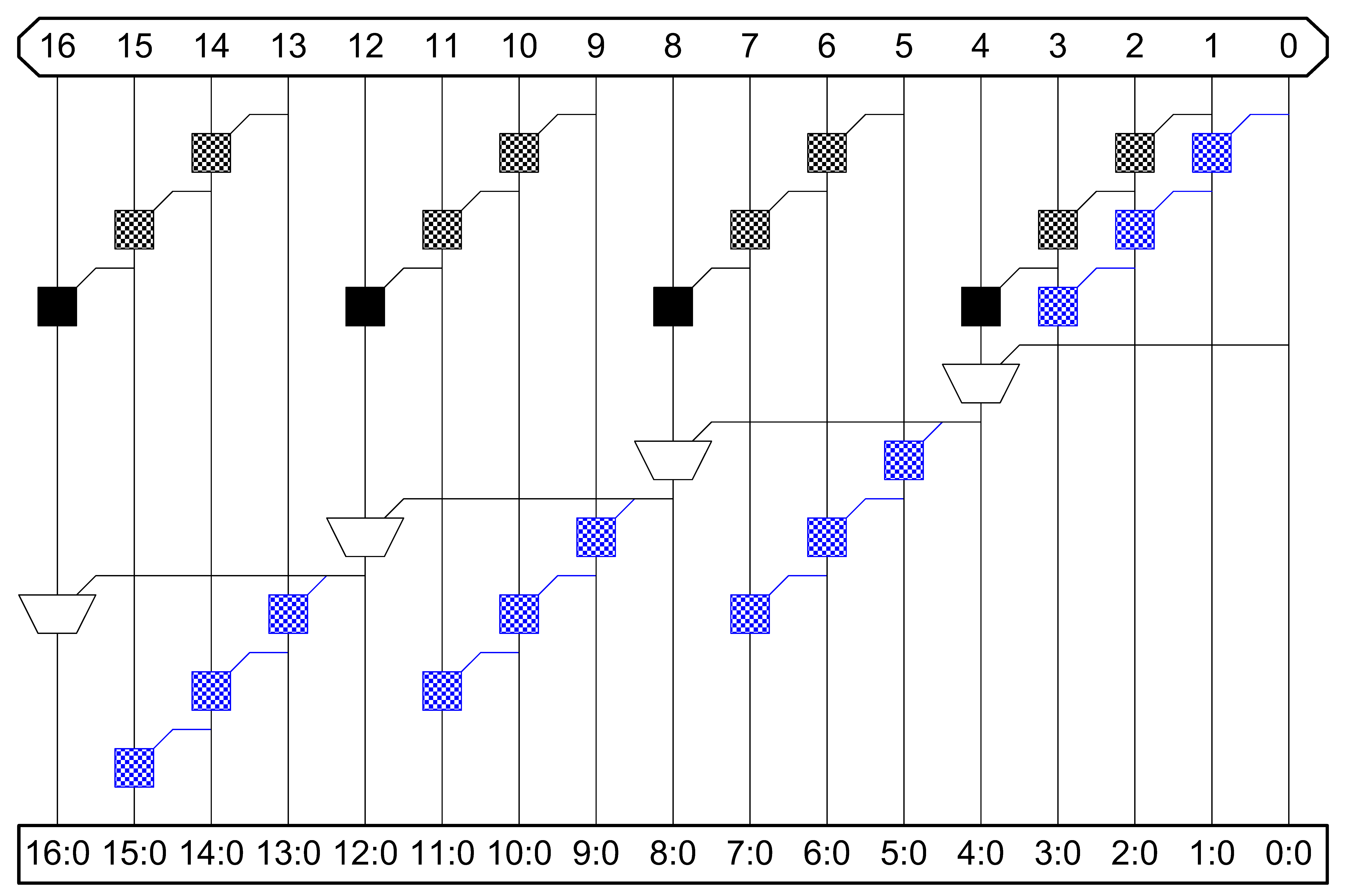
注意其中蓝色块也是 Gray cell,但是输入连在了最上面
4个一组:
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| N/4+5 | 3 | 1 | 1.25N~1.75N |
若可变组大小,延迟降低到 $O\left(\sqrt{N}\right)$
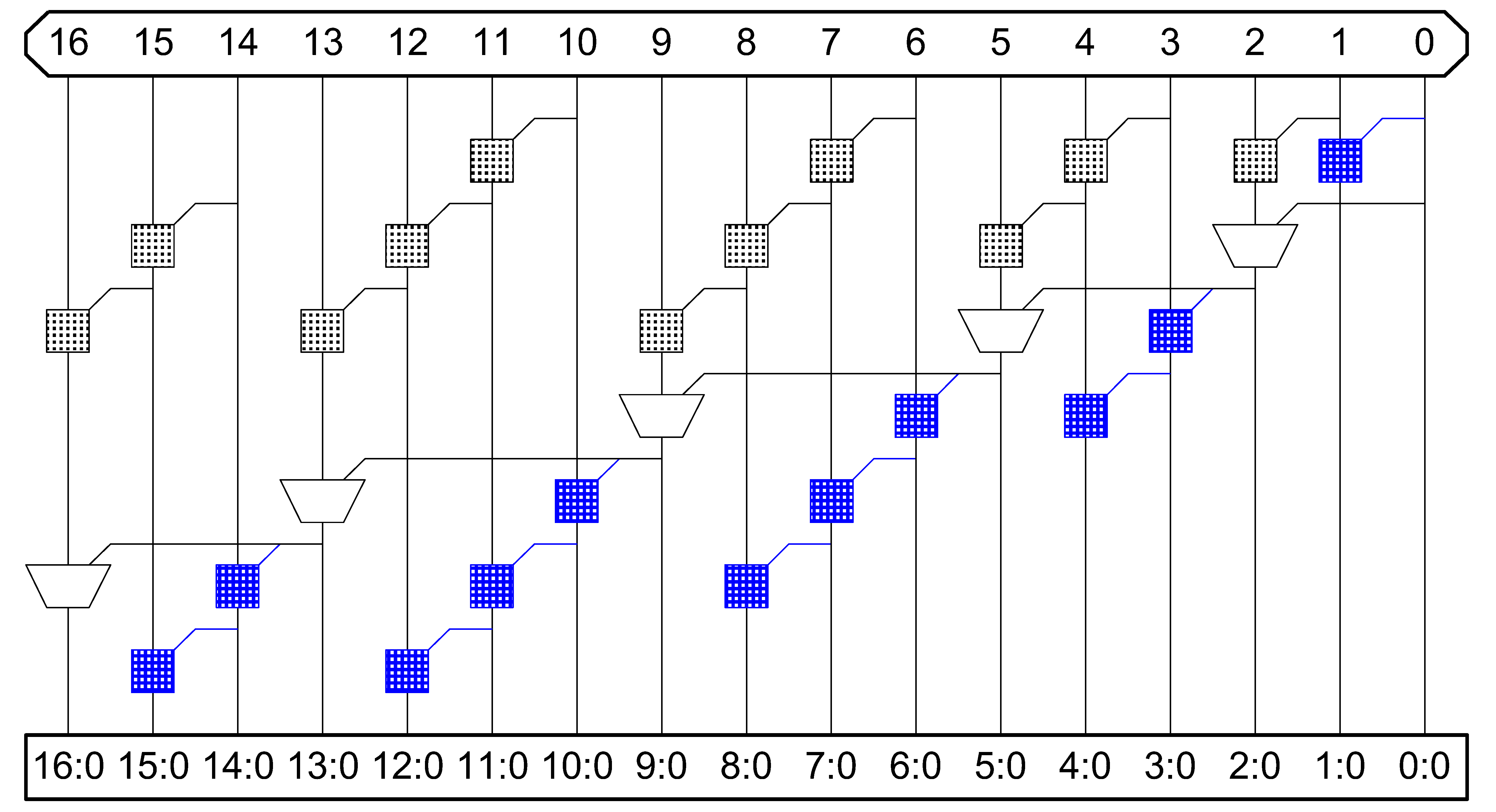
Carry-Increment Adder
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| N/2+2 | 5 | 1 | 1.75N-4 |
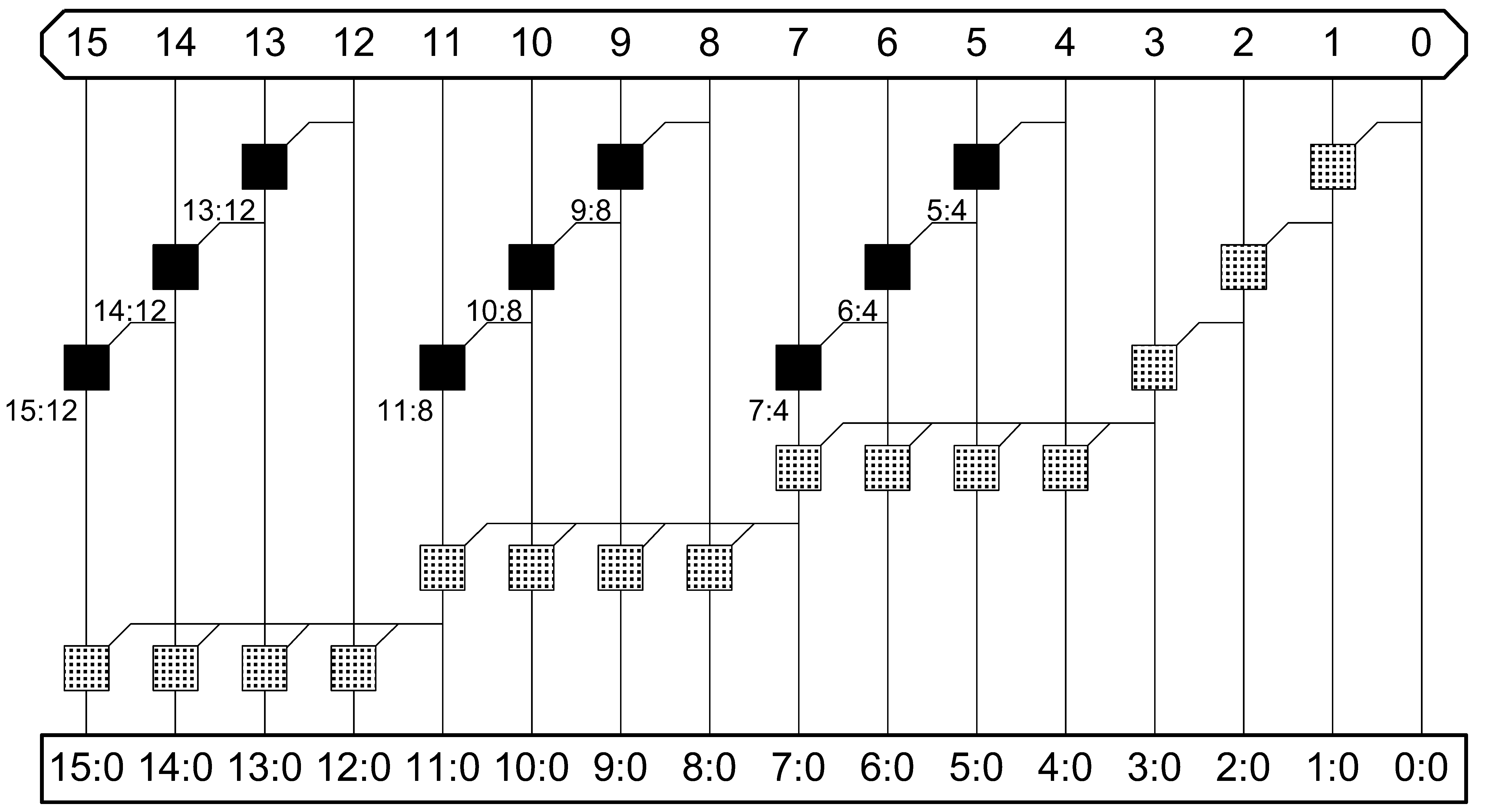
Brent-Kung*(B-tree)
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| $2\log_{2} N-1$ | 2 | 1 | 2N |
Sklansky(S-Tree)
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| $\log_{2} N$ | N/2+1 | 1 | $0.5N\log_{2} N$ |
Kogge-Stone*(K-tree)
| Logic Level | Max Fanout | Tracks | Cells |
|---|---|---|---|
| $\log_{2} N$ | 2 | N/2 | $N\log_{2} N$ |
树加法器分类
定义三维空间 $(\lambda,f,t)$,树加法器的参数满足
- Logic Level:$L+\lambda$
- Max Fanout:$2^f+1$
- Wiring:$2^t$
则已知的树加法器都在平面 $\lambda+f+t=L-1$ 上
Carry-Select Adder
针对每四位,分别预测进位输入是 0/1,做两套电路,等真正的进位输入来了再过一个选择器。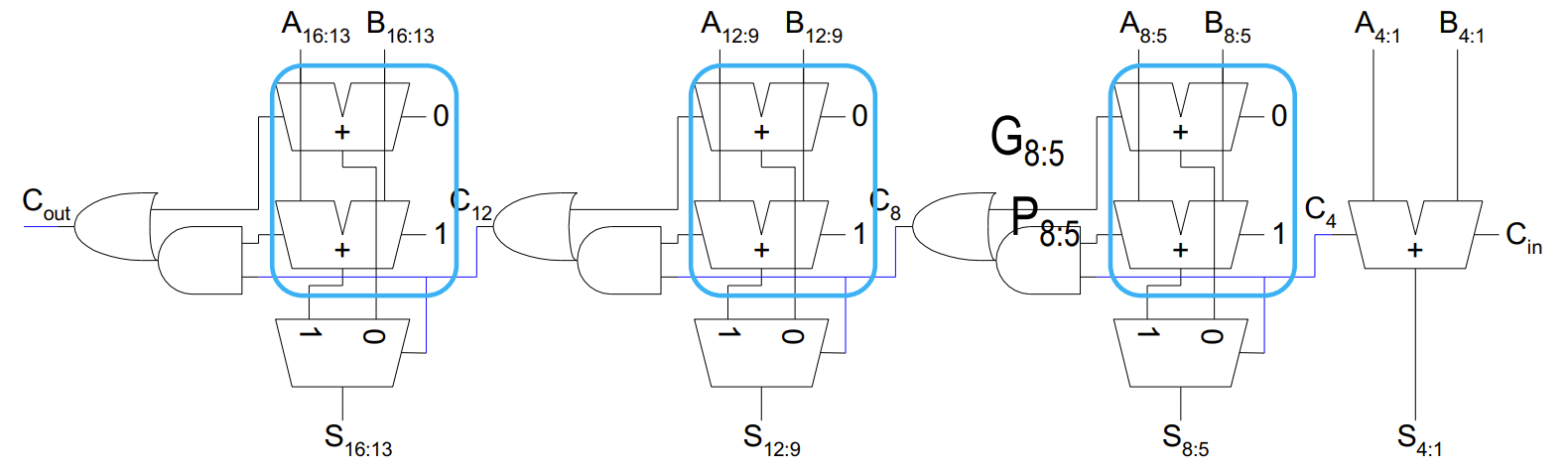
第八章 时序电路
相关概念
- 组合逻辑电路具有这样的特性:即逻辑块的输出仅是当前输入值的函数,假设逻辑门已经过了足够的时间来稳定。
- 然而,几乎所有有用的系统都需要存储状态信息,这类电路称为时序逻辑电路。
- 在时序逻辑电路中,输出不仅取决于输入的当前值,还取决于先前的输入值。换句话说,时序电路会记住系统过去的一些历史——它有记忆功能
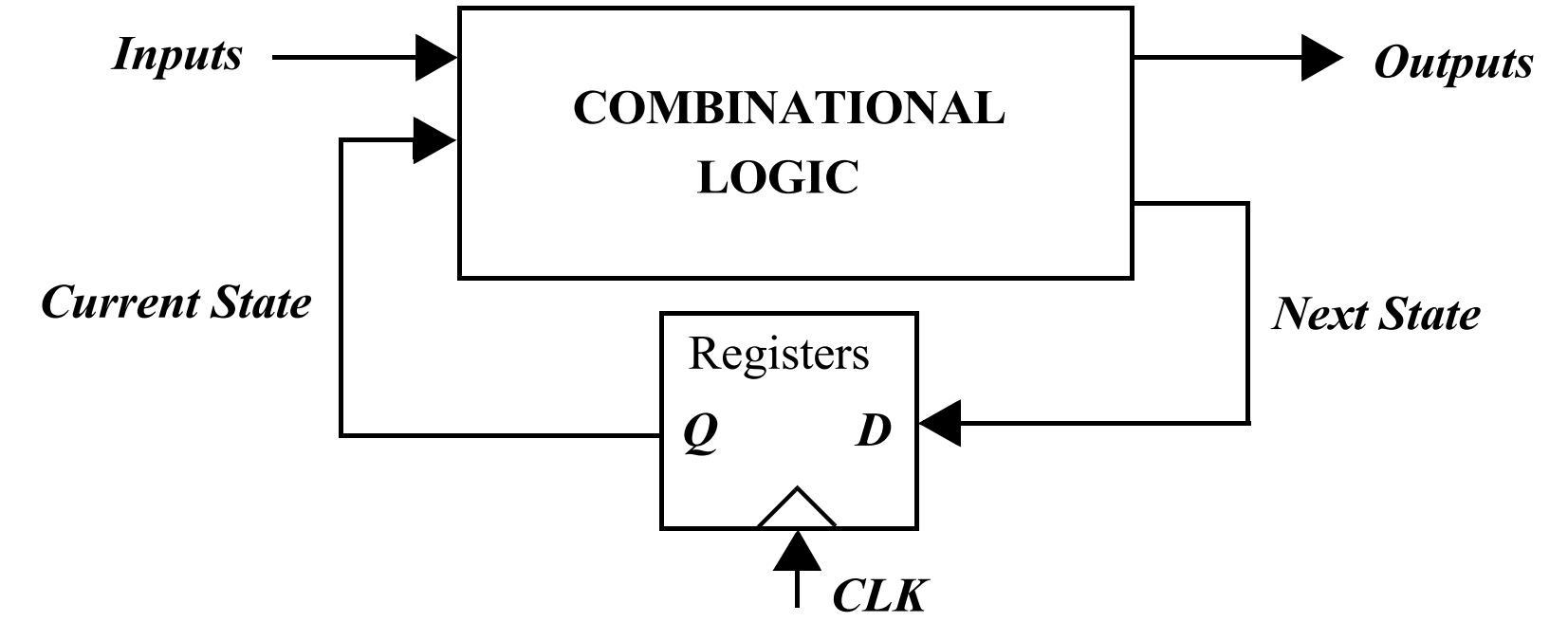
时序逻辑电路的整个系统可以用一个有限状态机(FSM)来描述,该机由组合逻辑和寄存器组成,寄存器用于保存系统状态。这里描述的系统属于同步时序系统的一类,其中所有寄存器都在单个全局时钟的控制下。FSM 的输出是当前输入和当前状态的函数。下一状态是根据当前状态和当前输入确定的,并被馈送到寄存器的输入。在时钟的上升沿,“下一状态”位被复制到寄存器的输出(经过一些传播延迟后),并开始一个新的周期。寄存器然后忽略输入信号的变化,直到下一个上升沿。通常,寄存器可以是正沿触发的(其中输入数据在时钟的正沿上被复制)或负沿触发的,其中输入数据被复制在负沿上,如时钟输入处的小圆所示)。
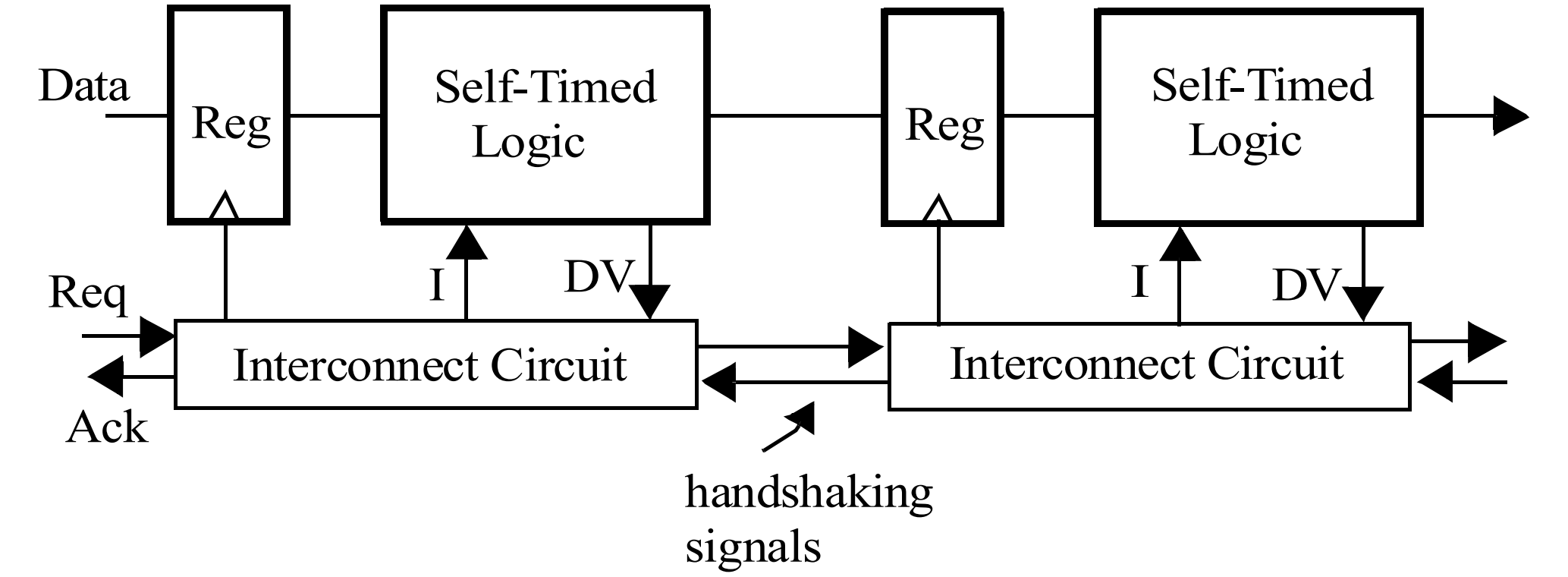
除了同步电路,还有异步电路
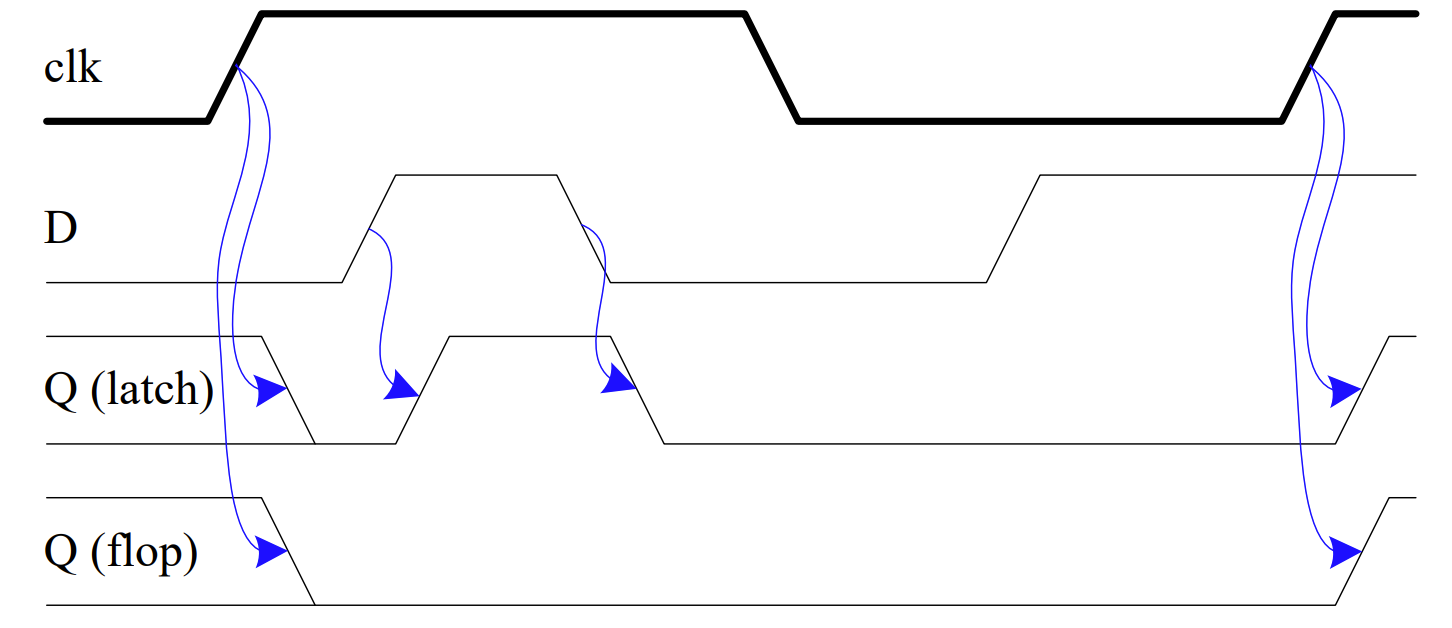
锁存器与触发器
| 锁存器 Latch | 触发器 Flip-Flop | |
|---|---|---|
| 条件 | 电平敏感 | 边沿敏感 |
时间定义
- 建立时间 Setup time: the time that the data inputs must be valid before clock transition
- 保持时间 hold time: the time that the data must remain valid after the clock transition
- 组合逻辑的传播延时指的是从组合逻辑电路的输入端发生变化到输出端产生响应(稳定)所需的最长时间
- 污染延时指的是在组合逻辑电路中,当一个输入信号发生变化时,导致输出信号的变化所需的最短时间
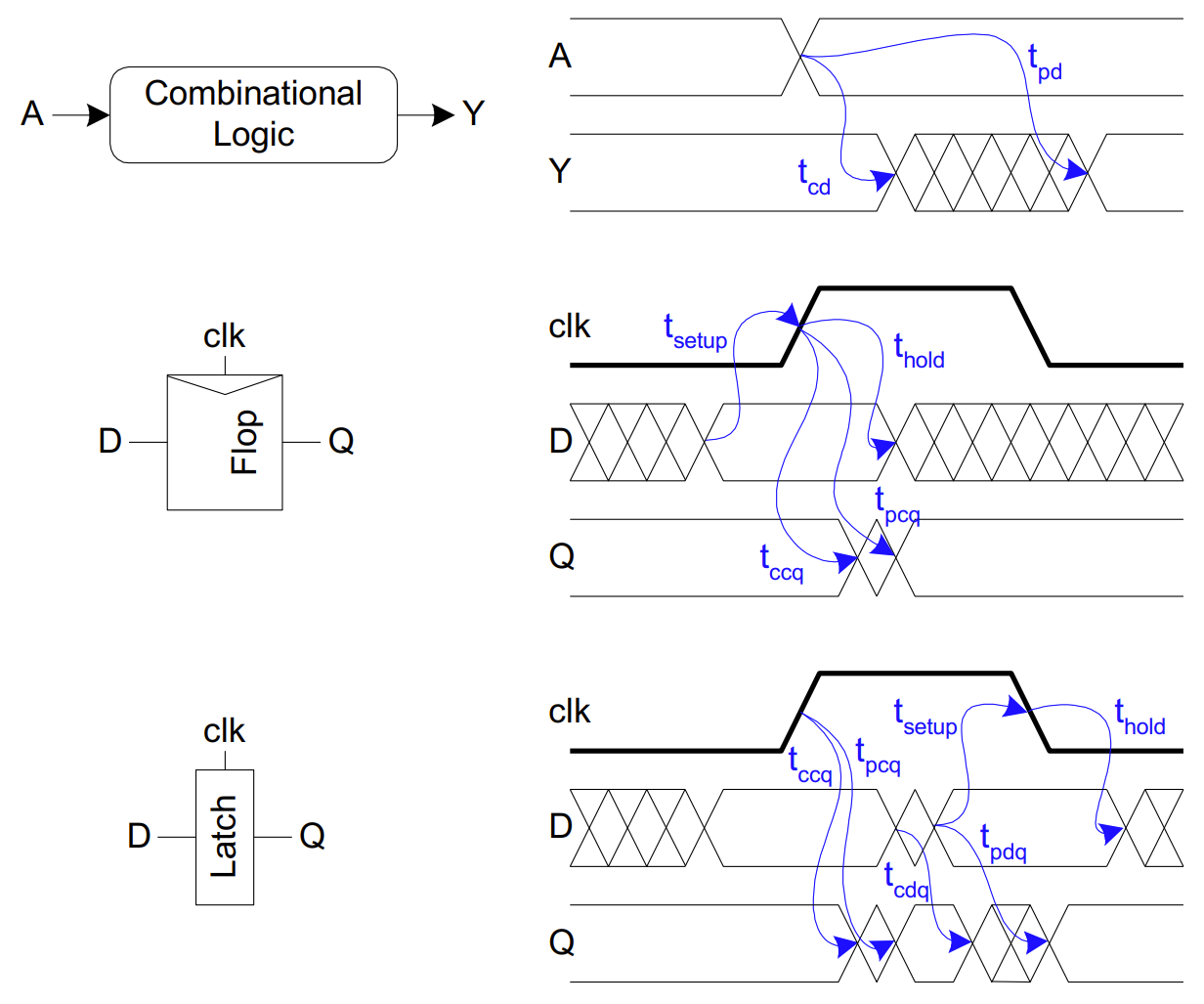
- $t_{pd}$:组合逻辑传播延时
- $t_{cd}$:组合逻辑污染延时
- $t_{pcq}$:Latch/FF 从时钟 Clk 到 输出 Q 的传播延时
- $t_{ccq}$:Latch/FF 从时钟 Clk 到 输出 Q 的污染延时
- $t_{pdq}$:Latch 从输入 D 到 输出 Q 的传播延时
- $t_{cdq}$:Latch 从输入 D 到 输出 Q 的污染延时
- $t_{setup}$:Latch/FF 建立时间
- $t_{hold}$:Latch/FF 保持时间
时间约束
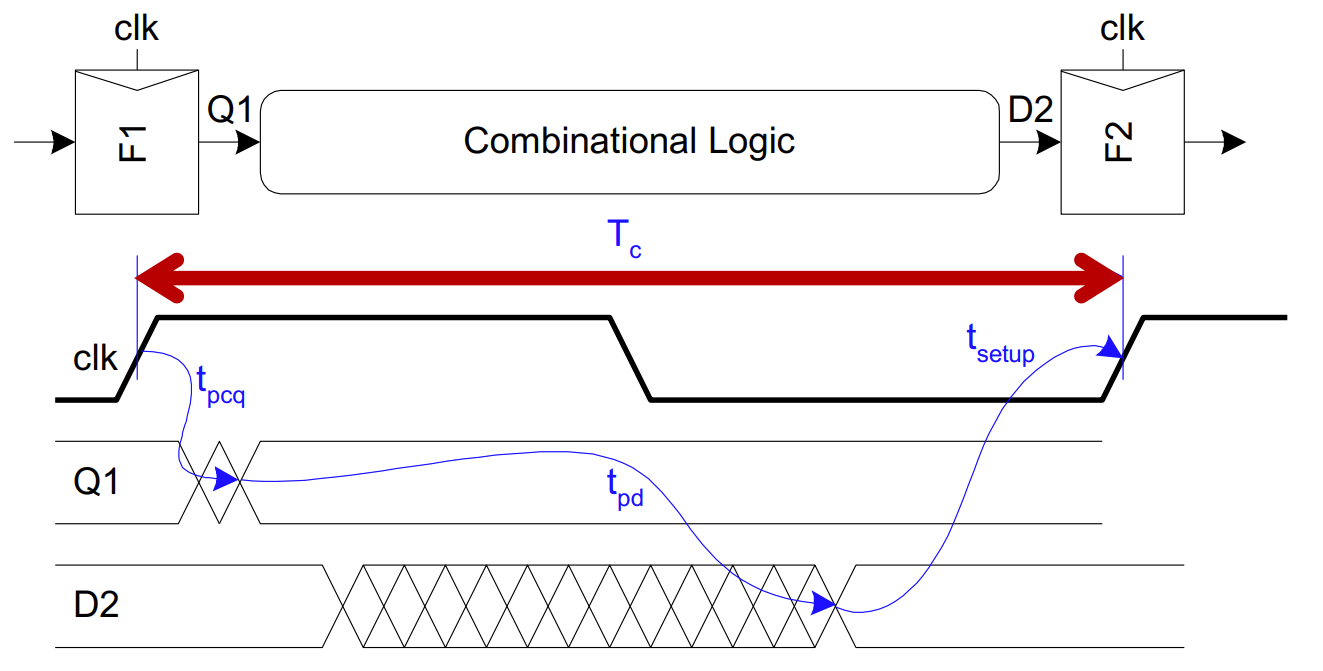
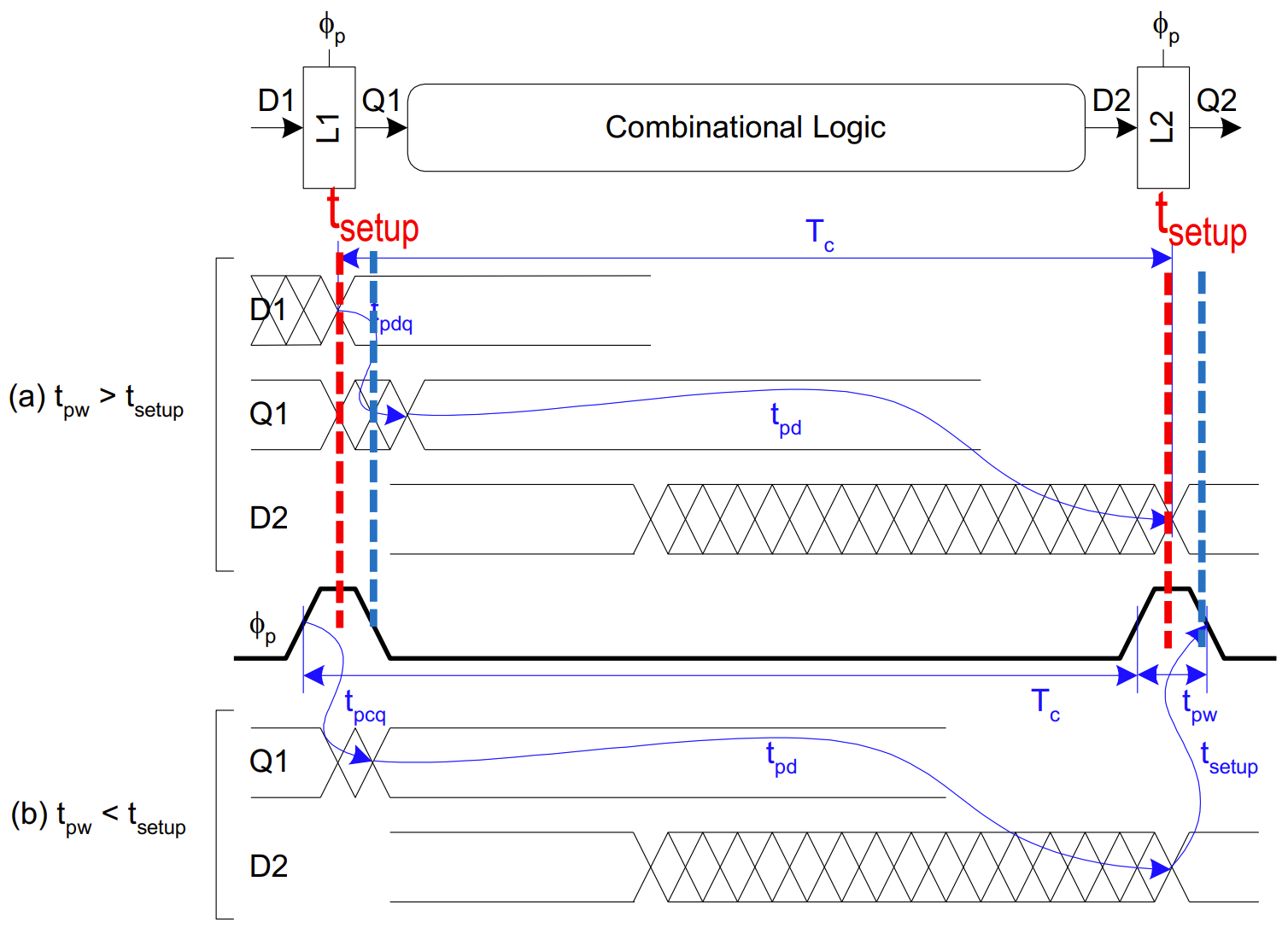
FF
建立时间约束:
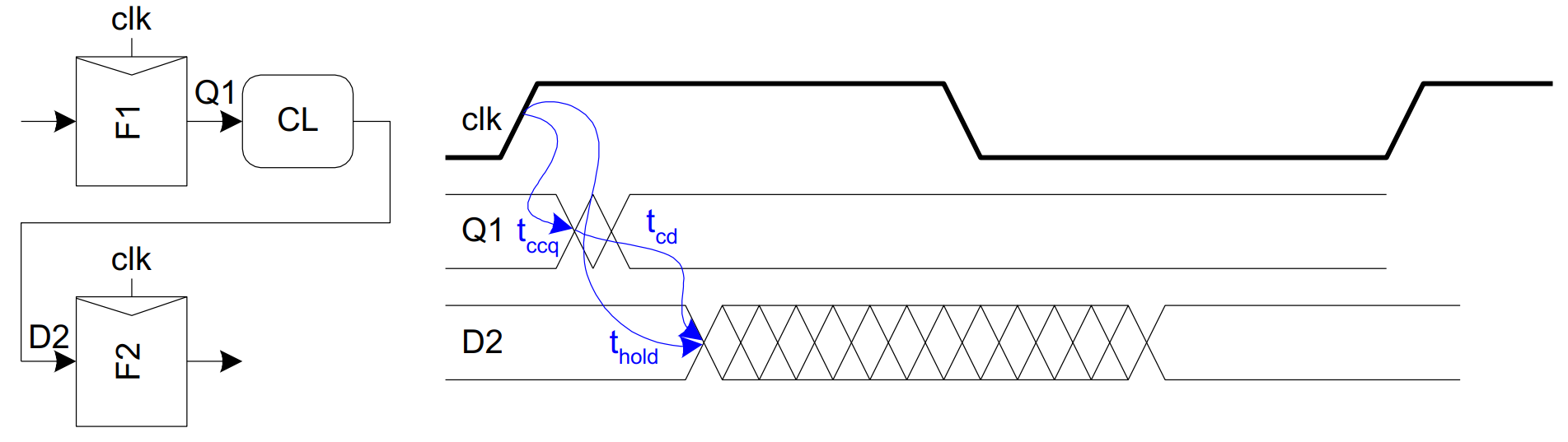
保持时间约束:
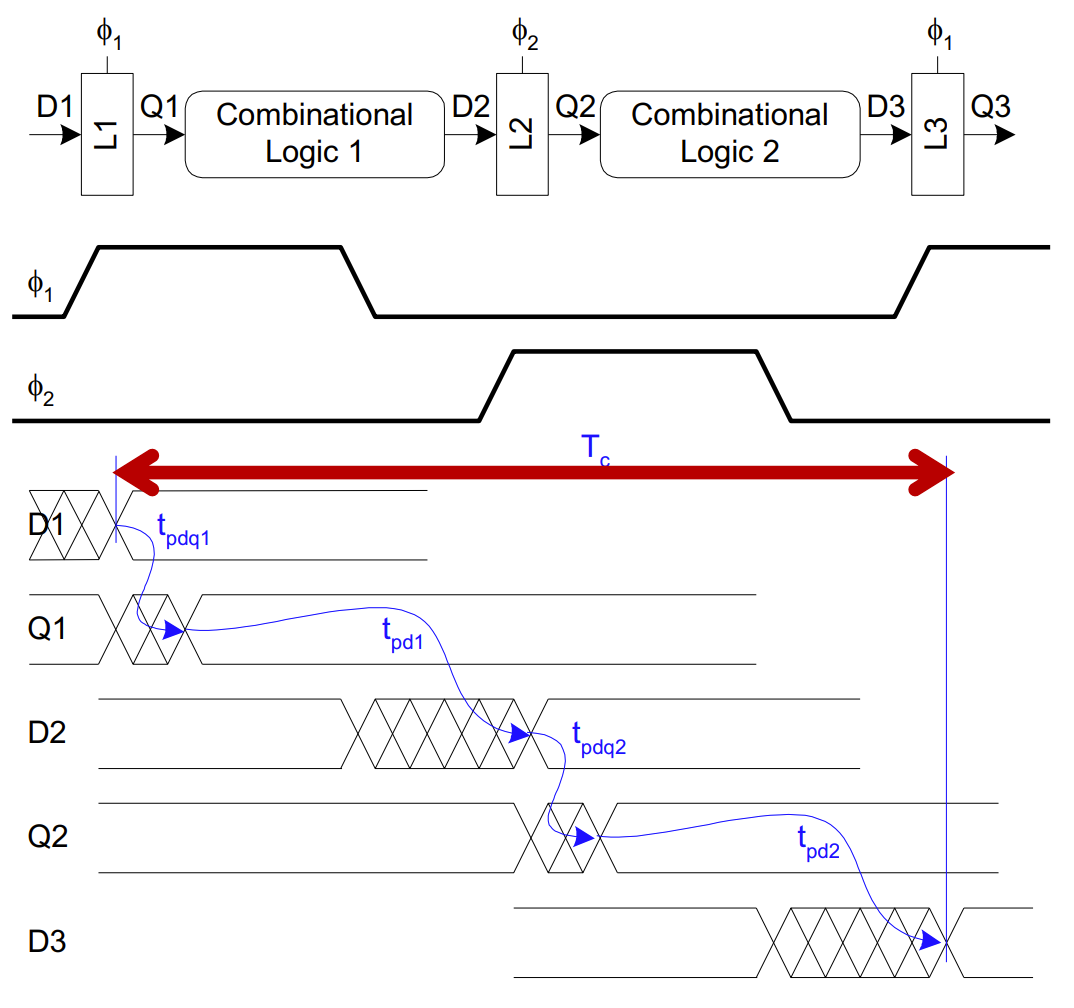
2-Phase Latches
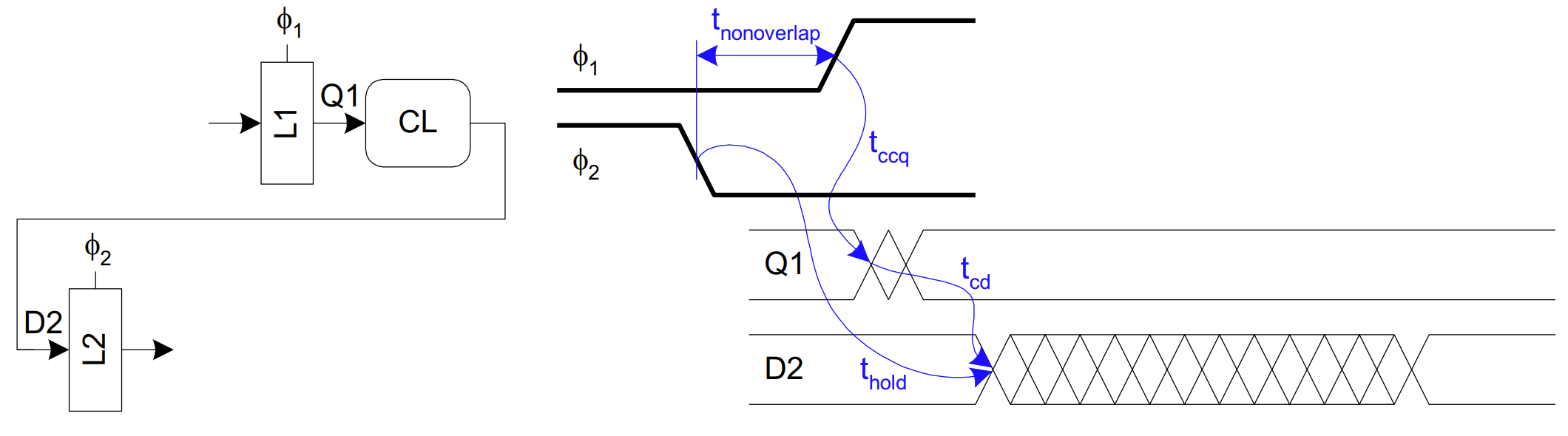
Pulsed Latches
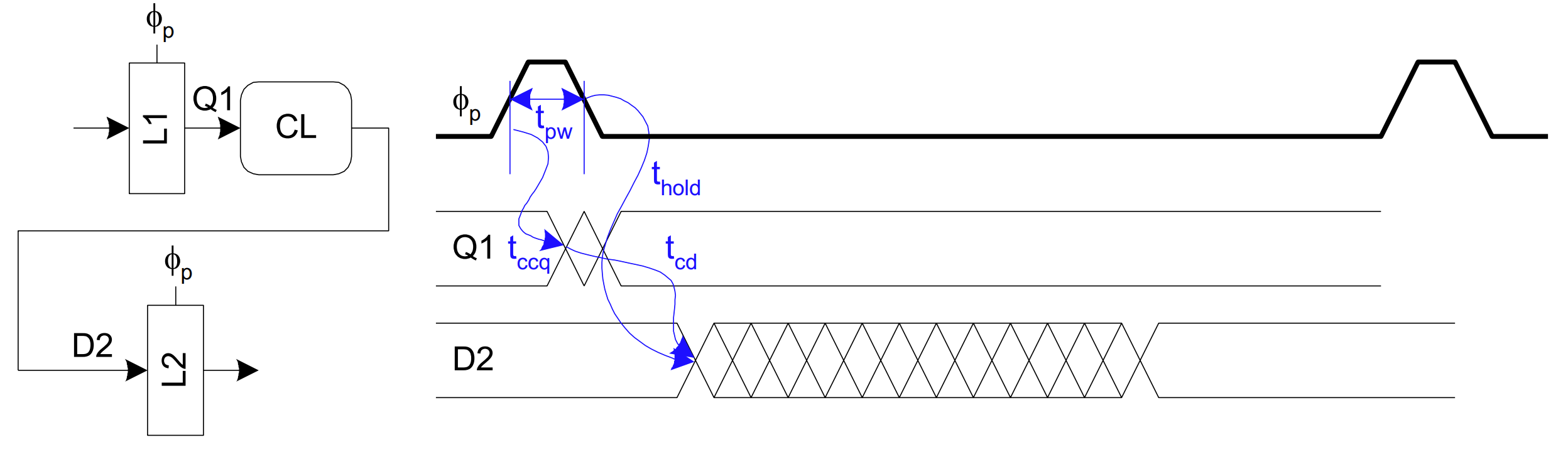
- Clock ready FIRST
- Data ready FIRST
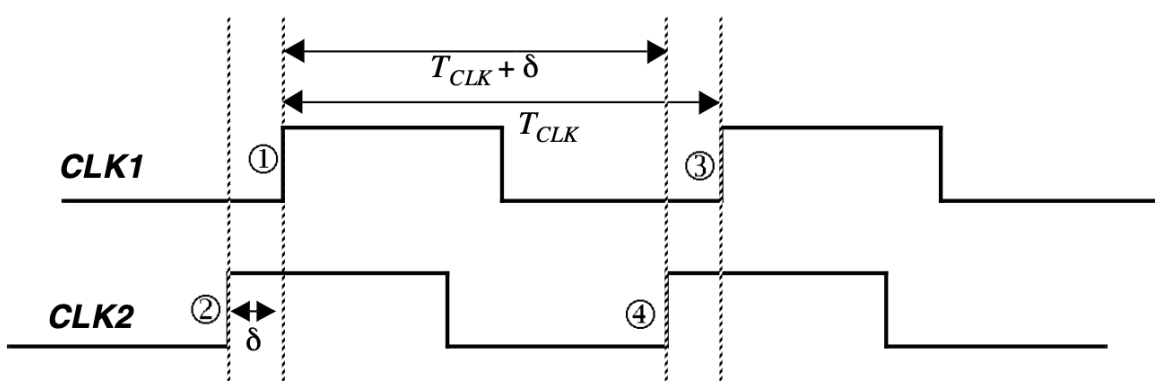
Clock skew(时钟偏移)
- 定义:The spatial(空间的) variation in arrival time of a clock transition
- 来源:Static path-length mismatches in the clock paths and differences in the clock load
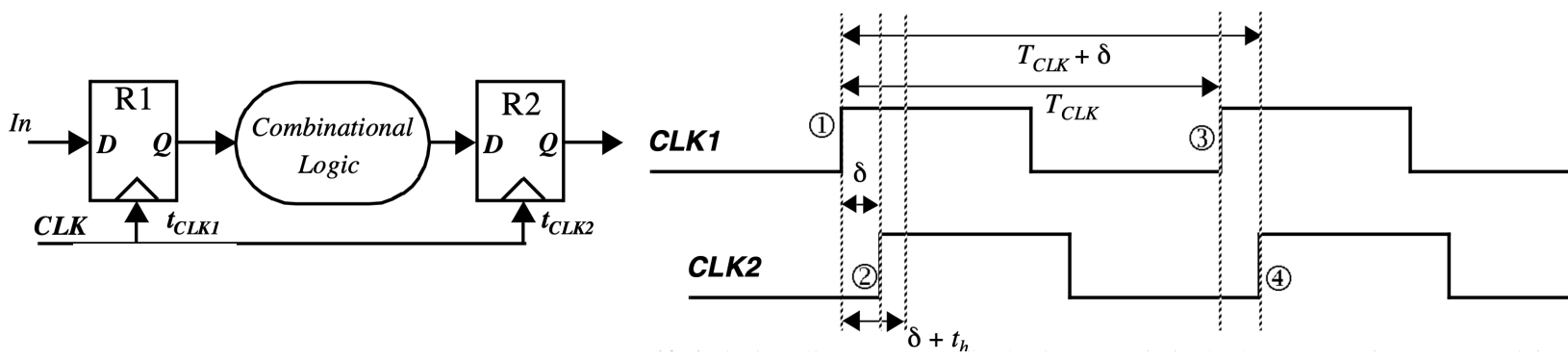
正负偏移
- 正偏移:Data flow/clock flow are the same direction
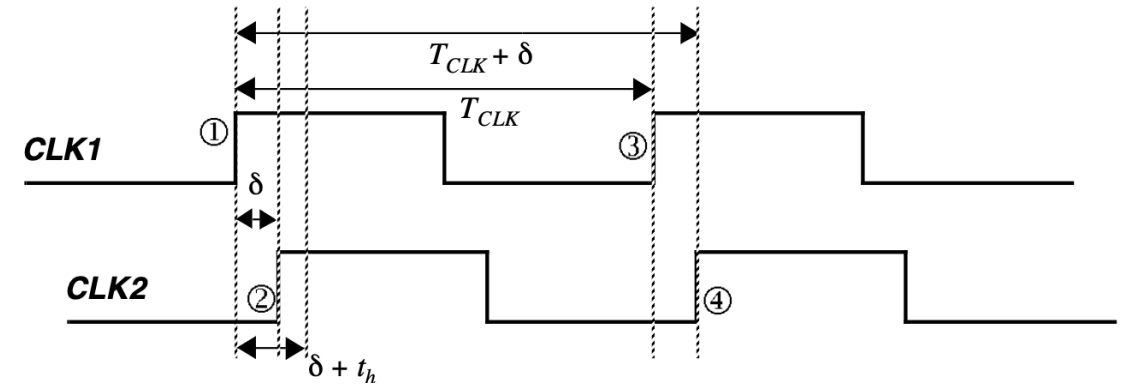
- 负偏移:Data flow/clock flow are the opposite direction
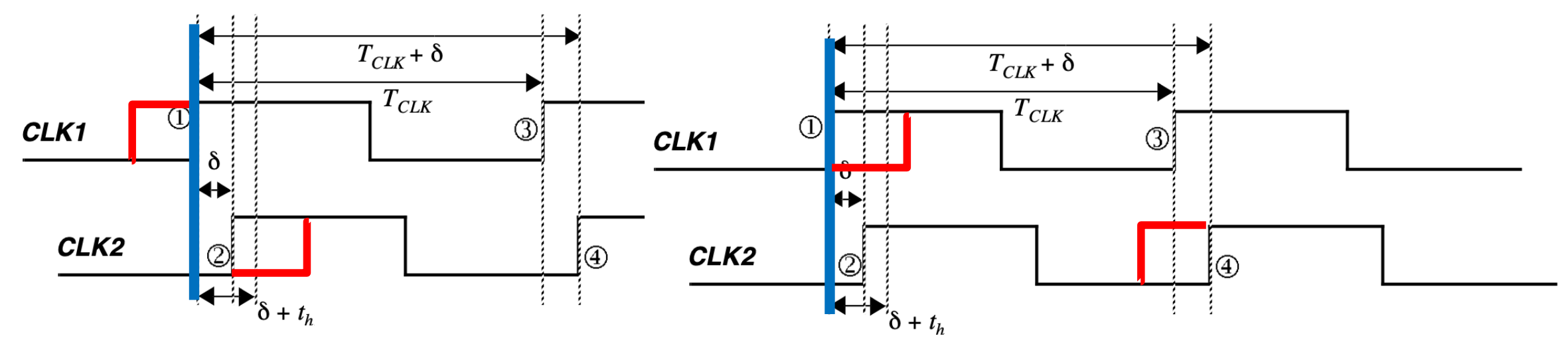
Clock Jitter(时钟抖动)
- 定义:Clock jitter refers to the temporal(时间的) variation of the clock period at a given point
- 来源:晶振的不稳定性,温度变化
本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 协议 ,转载请注明出处!