MOSFET

MOSFET 结构

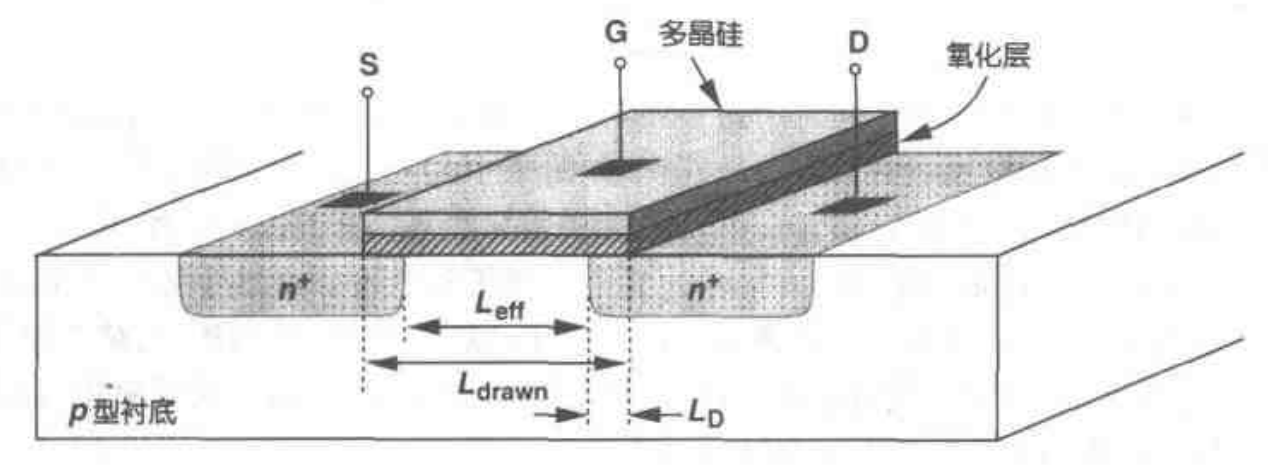
源漏方向的栅的尺寸叫栅长 $L$，与之垂直方向的栅的尺寸叫做栅宽 $W$。由于在制造过程中，源/漏结的横向扩散，源漏之间实际的距离略小于 $L_{0}$。为了避免混淆，我们定义 $L_{\mathrm{eff}}= L_{\mathrm{drawn}}-2 L_{\mathrm{D}}$，式中 $L_{\mathrm{cff}}$ 称为有效沟道长度，$L_{\mathrm{drawn}}$ 是沟道总长度，而 $L_{\mathrm{D}}$ 是横向扩散的长度。

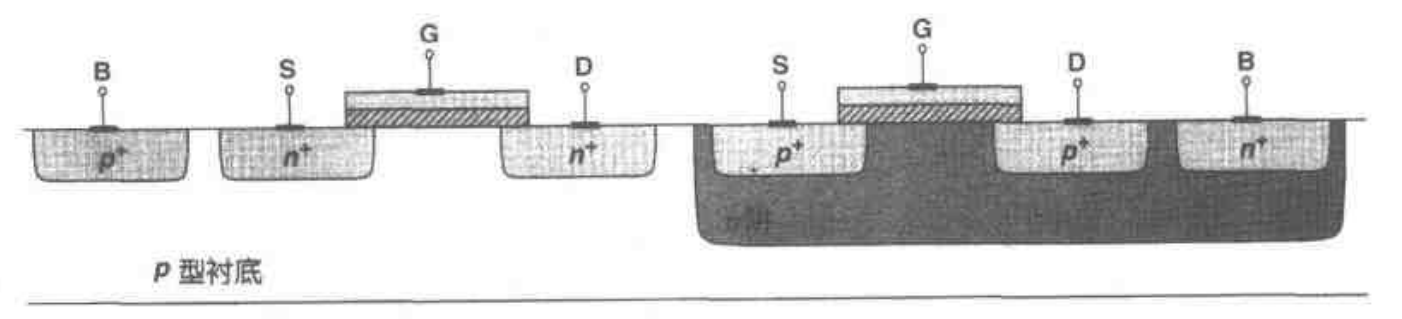
在互补 $MOS$（CMOS）技术中同时用到 $NMOS$ 和 $PMOS$。从简单的角度来看，$PMOS$ 器件可通过将所有掺杂类型取反（包括衬底）来实现。但实际生产中，$NMOS$ 和 $PMOS$ 器件必须做在同一晶片上，也就是说做在相同的衬底上。由于这一原因，其中某一种类型的器件要做在一个“局部衬底”上，通常称为“阱”。现在大多数 $CMOS$ 工艺中，$PMOS$ 器件做在 n 阱中。注意 n 阱必须接一定的电位，以便 $PMOS$ 管的源偏结二极管在任何情况下都保持反偏。在大多数电路中，n 阱与最正的电源供给相连接。

I/V特性

阈值电压

$$\begin{align} V_{t} & = V_{g}|_{threshold} \\ & = \left(V_{fb}+V_{s}+V_{ox}\right)|_{threshold}\\ &=V_{fb}+2V_{B}-\frac{Q_s}{C_{ox}}\\ &=V_{fb}+2V_{B}+\frac{qN_aW_{dep}}{C_{ox}}\\ &=V_{fb}+2V_{B}+\frac{\sqrt{qN_a2\varepsilon_s2V_B}}{C_{ox}}\\ \end{align}$$

• 截止区 $V_{GS}<V_{th}$ $$I_D=0$$
• 弱反型/亚阈值区 $V_{GS}<V_{th}$ 且 $V_{GS}\approx V_{th}$ $$I_{D,wi}=I_{D,t}\frac{W}{L}e^{\frac{V_{GS}-V_{th}}{nU_T}},\quad U_T=kT/q\approx 26\mathrm{mV}$$
• 线性区 $V_{GS}-V_{th}>V_{DS}$ $$I_{D} = \frac{W \mu_{n} C_{\mathrm{ox}}}{2 L}\left[2\left(V_{G S}-V_{th}\right) V_{D S}-V_{D S}^{2}\right]$$
• 饱和区 $V_{GS}-V_{th}<V_{DS}$ $$I_{D}=\frac{W \mu_{n} C_{ox}}{2 L}\left(V_{G S}-V_{th}\right)^{2}(1+\lambda V_{DS})$$

小信号分析

等效模型的参数

跨导是衡量栅极电压变化时漏极电流变化强度的指标

• 决定 MOSFET 的增益和速度
• 饱和区的跨导最高
• 弱反转区的跨导效率最高，即 $g_m/I_D$

饱和跨导 $g_{m}$

$$g_{m}=\frac{\partial I_{D}}{\partial V_{G S}}=\mu_{n} C_{o x} \frac{W}{L}\left(V_{G S}-V_{t h}\right)=\sqrt{\mu_{n} C_{o x} \frac{W}{L} 2 I_{D}}=\frac{2 I_{D}}{V_{G S}-V_{t h}}$$

体跨导 $g_{mb}$

$$\begin{aligned} g_{m b} & =\frac{\partial I_{D}}{\partial V_{B S}} \\ & =\mu_{n} C_{o x} \frac{W}{L}\left(V_{G S}-V_{t h}\right)\left(-\frac{\partial V_{t h}}{\partial V_{B S}}\right) \\ & =g_{m}\left(\frac{\gamma}{2 \sqrt{\left|2 \varphi_{F}+V_{S B}\right|}}\right) \end{aligned}$$

输出电阻 $r_o$/输出电导 $g_o$

$$\begin{aligned} r_o & =\left(\frac{\partial I_{D}}{\partial V_{DS}}\right)^{-1} \\ &=\frac{1}{\lambda I_D}=\frac{V_EL}{I_D} \end{aligned}$$

本征电容 $C_{gs}$、$C_{gd}$

工作区	$C_{gs}$	$C_{gd}$
截止	$WL_{ov}C_{ox}$	$WL_{ov}C_{ox}$
线性	$\frac{WLC_{ox}}{2}+WL_{ov}C_{ox}$	$\frac{WLC_{ox}}{2}+WL_{ov}C_{ox}$
饱和	$\frac{2WLC_{ox}}{3}+WL_{ov}C_{ox}$	$WL_{ov}C_{ox}$

其中

• $L$ 是有效沟道长度
• $L_{ov}$ 是漏源扩散到栅氧化层下面的长度

寄生电容

$$C_{s b}=\frac{C_{s b 0}}{\sqrt{1+\frac{V_{S B}}{\psi_{0}}}} \quad C_{d b}=\frac{C_{d b 0}}{\sqrt{1+\frac{V_{D B}}{\psi_{0}}}}$$

或者见 https://teru.space/2023/09/13/%E6%95%B0%E5%AD%97%E9%9B%86%E6%88%90%E7%94%B5%E8%B7%AF%E8%AE%BE%E8%AE%A1%E7%AC%94%E8%AE%B0/#%E6%89%A9%E6%95%A3%E7%94%B5%E5%AE%B9

简化模型

$$i_{ds}=g_m\cdot v_{gs}+g_{mb}\cdot v_{bs}+\frac{1}{r_o}\cdot v_{ds}$$

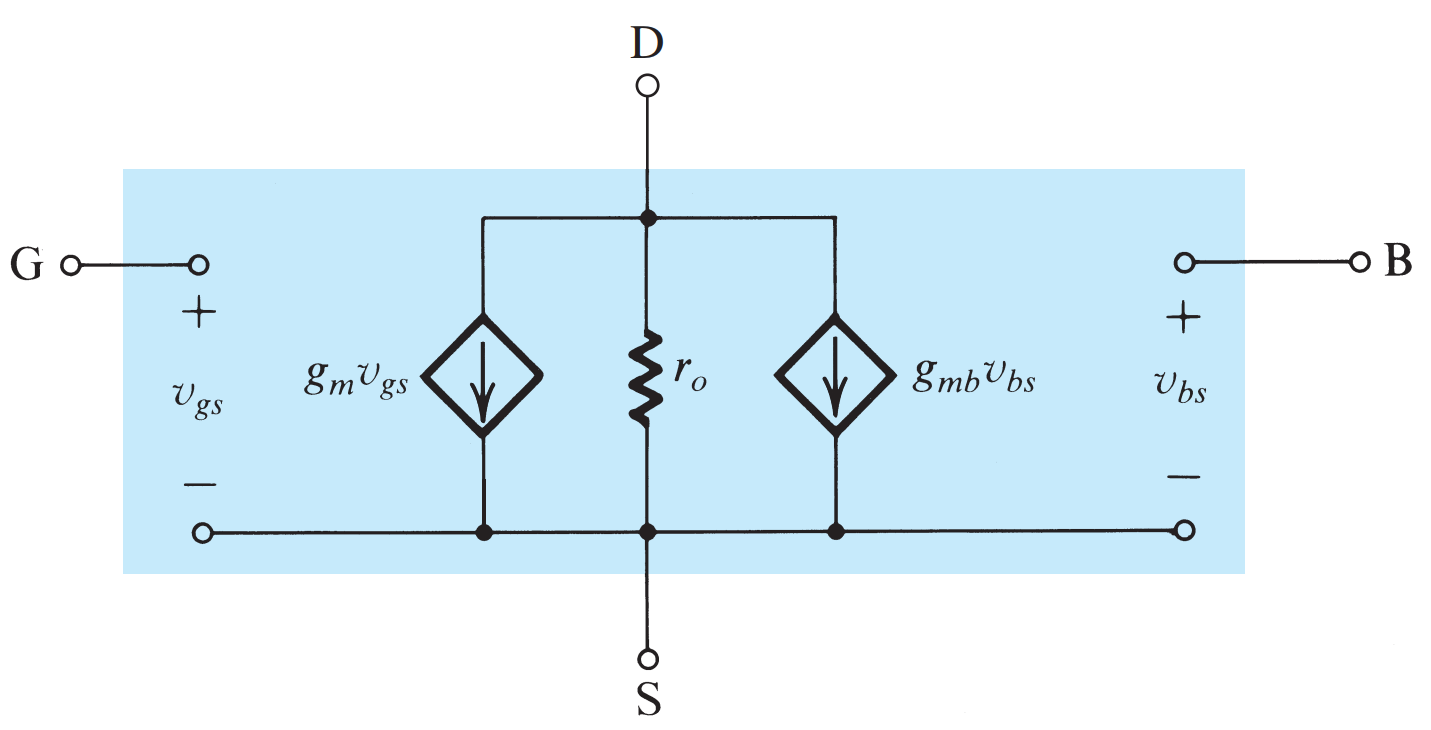
完整模型

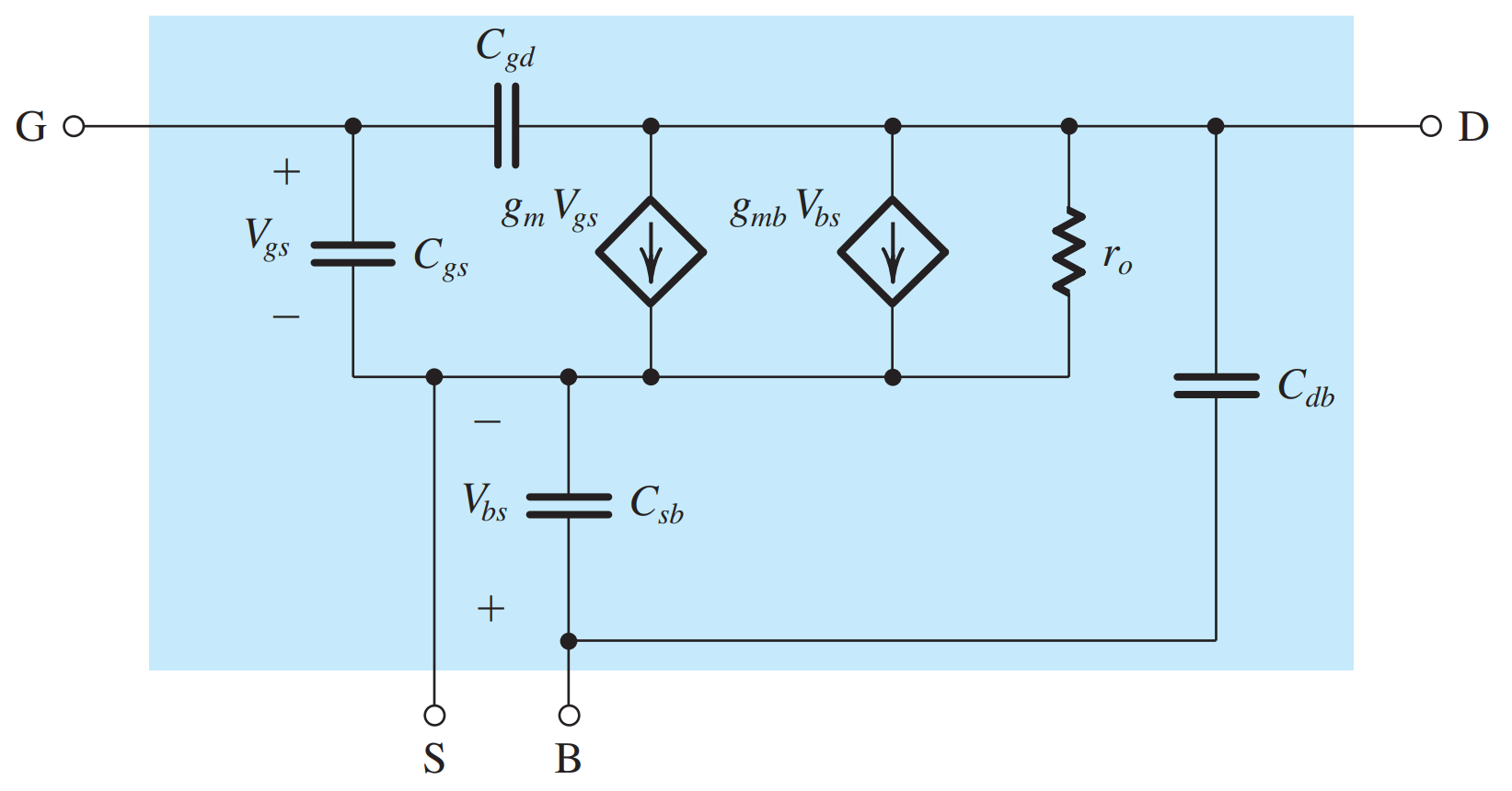
单级放大器

这可能是这门课最基础也是最重要的一节了。然而 Razavi 的教材实在是有些抽象，跳跃性比较强。PPT 内容全面，但是仍有不少坑与细节问题。故此节打算自己写，不照抄 PPT 和课本了。

放大的原理

• 模电里就学过，放大是针对小信号而言的
• MOSFET工作在某个直流稳态，然后把小信号叠加到输入上，输出也会发生变动
• 由于小信号很小，变动在整个系统的输入输出曲线上只占很小一部分，因此可以看成在这一点的切线上变动
• 如果切线斜率大于1，那么输入变化x，输出可能变化2x，这就实现了放大
• 显然小信号必须足够小，否则就不再是线性的了
• 使用MOSFET实现时，在理论分析中，小信号等效电路中的受控电流源就是放大的核心组件

共源放大器

共源（CS）放大器；输入应用于栅极(G)，输出取自漏极(D)，源极(S)是输入和输出的共同参考点（小信号共地）

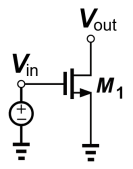
↑注意 Razavi 的这个图画得很糟糕，这里的 $V_{in}$ 应该是包含了大信号和小信号两部分的。

小信号等效电路中：

• 跨导 $$g_{m}=\mu_{n} C_{o x} \frac{W}{L}\left(V_{G S}-V_{t h}\right)=\sqrt{\mu_{n} C_{o x} \frac{W}{L} 2 I_{D}}=\frac{2 I_{D}}{V_{G S}-V_{t h}}$$
• 输出电阻 $$r_{o}=\frac{1}{\lambda I_{D}}=\frac{V_{E} L}{I_{D}}$$

在接下去的分析中，我们将 CS 放大器的 $V_{out}$ 和地作为含源一端口网络的两个端。

使用诺顿定理，可以用一个电流源与一个电阻并联组合来等效。由于小信号电路都是线性电路，且输入小信号为 0 时输出也为 0，不难得出结论：可以把诺顿等效电流源当成受控电流源，与 $V_{in}$ 成正比例关系。

于是定义受控电流源的系数为等效跨导 $G_{m}$，电阻为输出阻抗 $Z_{out}$

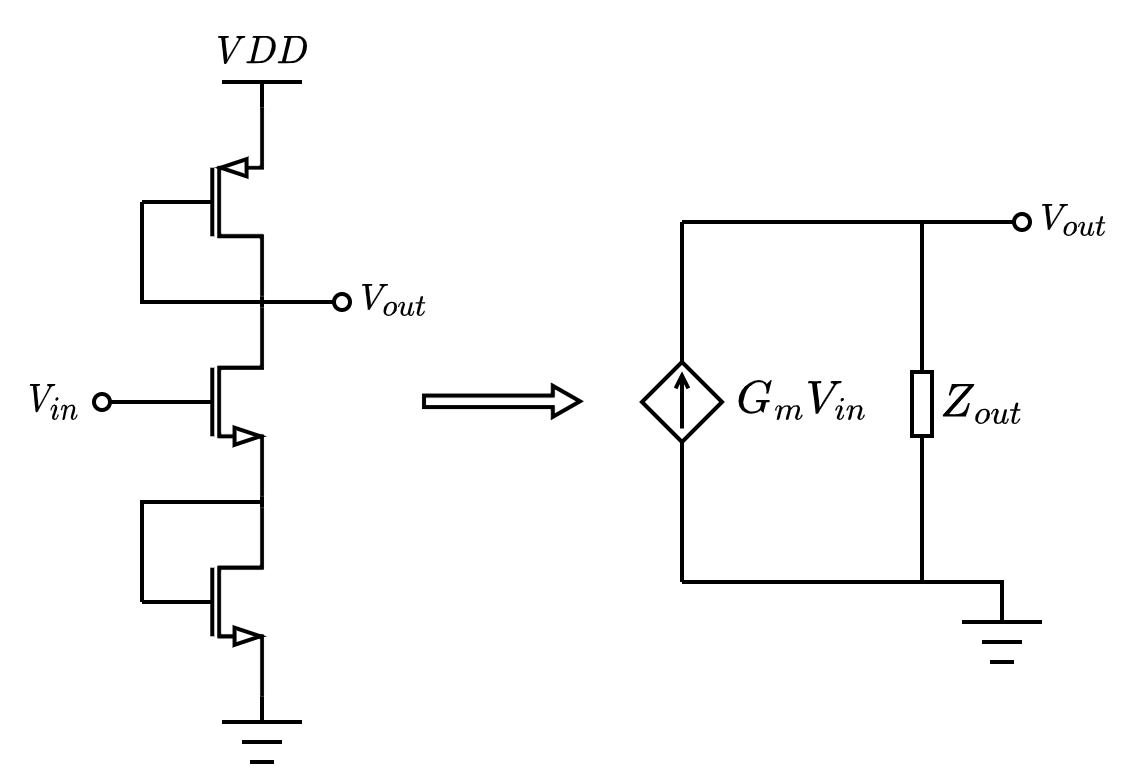
接电阻的共源放大器

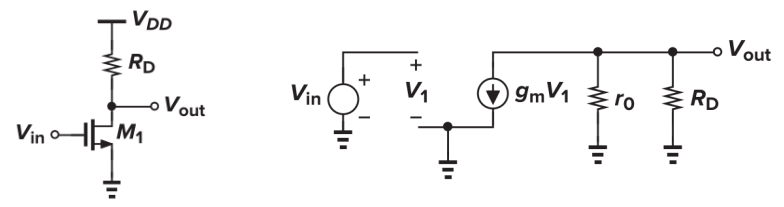
• 等效跨导 $$G_m=-g_{m1}$$
• 输出阻抗 $$R_{out}=r_{o1}//R_{D}$$
• 电压增益 $$A_{v}=-g_{m1}\left(r_{o1} // R_{D}\right)$$

Insights：

• 电阻负载具有有限阻抗，从而降低了小信号增益
• 难以制造物理尺寸合理的大型电阻器
• 难以制造具有严格控制值的电阻器（用于精确增益）

接深三极管区MOSFET的共源放大器（不常用）

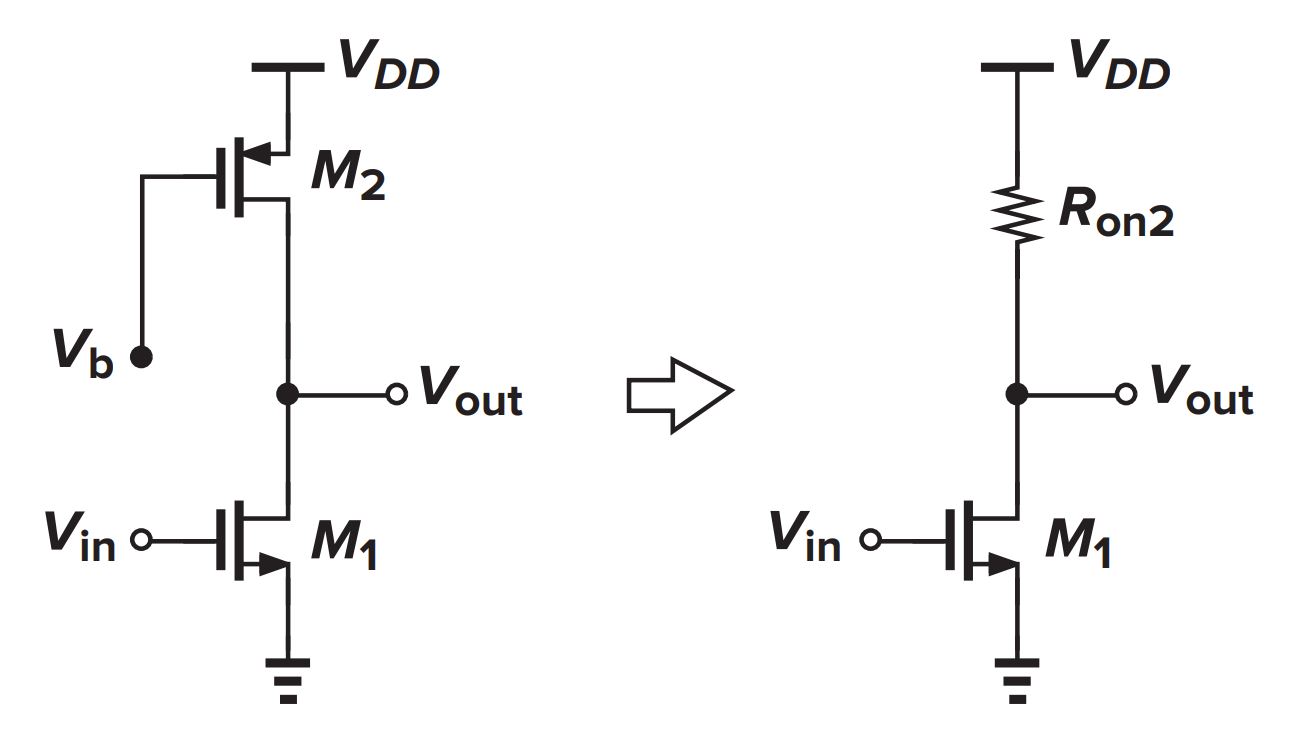
这个时候小信号模型失效了，但是 M2 可以直接看成电阻，

$$R_{\text {on2 } }=\frac{1}{\mu_{p} C_{o x}(W / L)_{2}\left(V_{D D}-V_{b}-\left|V_{\text {thp }}\right|\right)}$$

• 等效跨导 $$G_m=-g_{m1}$$
• 输出阻抗 $$R_{out}=r_{o1}//R_{on2}$$
• 电压增益 $$A_{v}=-g_{m1}\left(r_{o1} // R_{on2}\right)$$

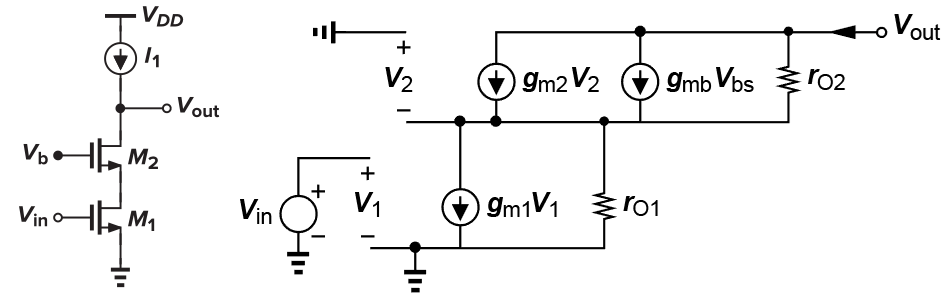
接饱和区MOSFET的共源放大器

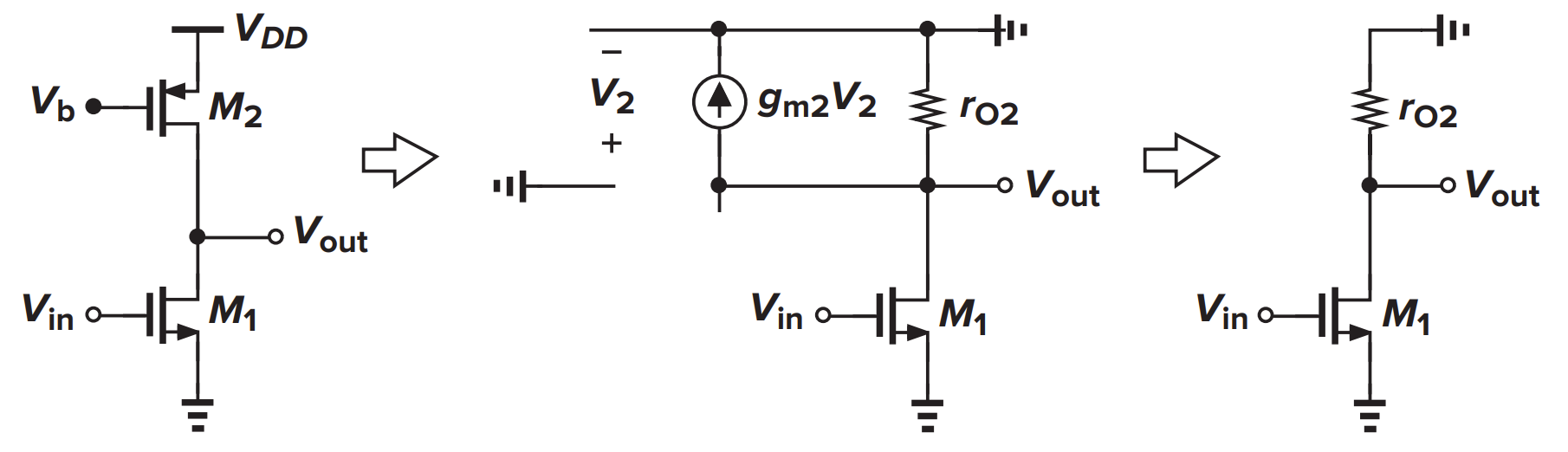
M2 在饱和区，理论上 $I_{D}$ 应该是关于 $V_{DS}$ 的常数函数，也就是电流始终不变，相当于一个电流源。但是由于沟长调制，$I_{D}$ 随 $V_{DS}$ 缓慢增加，因此等效小信号模型中还是存在一个电阻 $r_{o2}$

由于 $V_2$ 两端都是 DC 电压，于是在小信号模型中都是接地，$V_2=0$，受控电流源可以直接去掉。

• 等效跨导 $$G_m=-g_{m1}$$
• 输出阻抗 $$R_{out}=r_{o1}//r_{o2}$$
• 电压增益 $$A_{v}=-g_{m1}\left(r_{o1} // r_{o2}\right)$$

接类二极管MOSFET的共源放大器

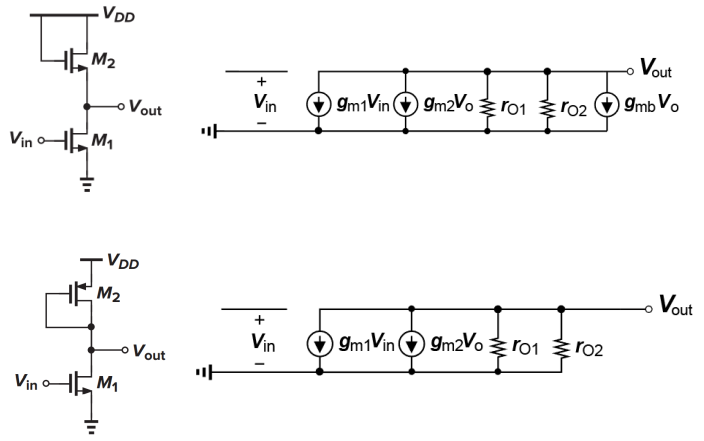
先考虑上图，等效小信号模型已经画出。注意 M2 是 NMOS 的情况，由于不是共源解法，所以需要考虑体偏效应。

• 等效跨导 $$G_m=-g_{m1}$$
• 输出阻抗 $$R_{out}=r_{o1}//\left( \frac{1}{g_{m2}+g_{mb2}} // r_{o2}\right)$$
• 电压增益 $$A_{v}=-g_{m1}\left(r_{o1}//\left( \frac{1}{g_{m2}+g_{mb2}} // r_{o2}\right)\right)$$

如果我们把这种二极管接法的 MOSFET 单独拿出来看，忽略衬底偏置效应，画出小信号模型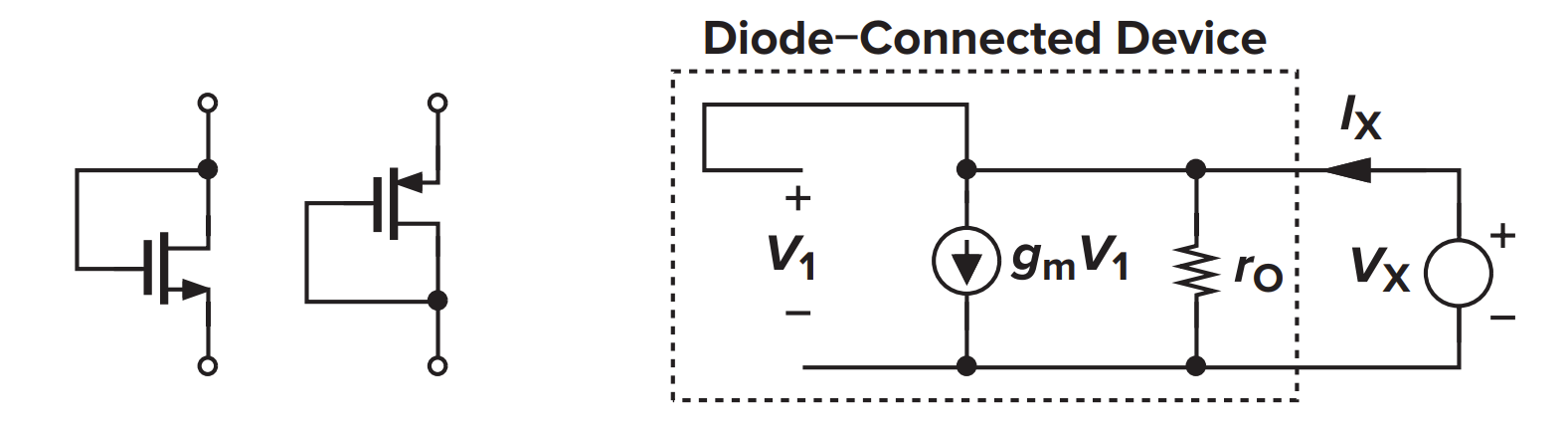

稍加计算可得这个 MOSFET 等效为一个电阻，阻抗为

$$\frac{1}{g_{m}} // r_{o}$$

（如果有衬底偏置就不能这么玩）

接电流源的共源放大器

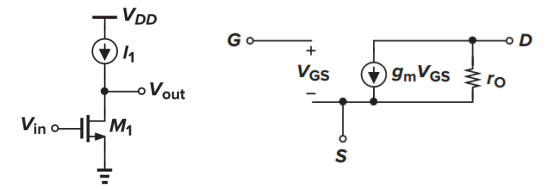
注意在交流通路中，电流源是断路。这个其实就相当于接电阻的 CS，但是电阻是无穷大。

• 等效跨导 $$G_m=-g_{m1}$$
• 输出阻抗 $$R_{out}=r_{o1}$$
• 电压增益 $$A_{v}=-g_{m1}r_{o1}$$

像反相器的共源放大器

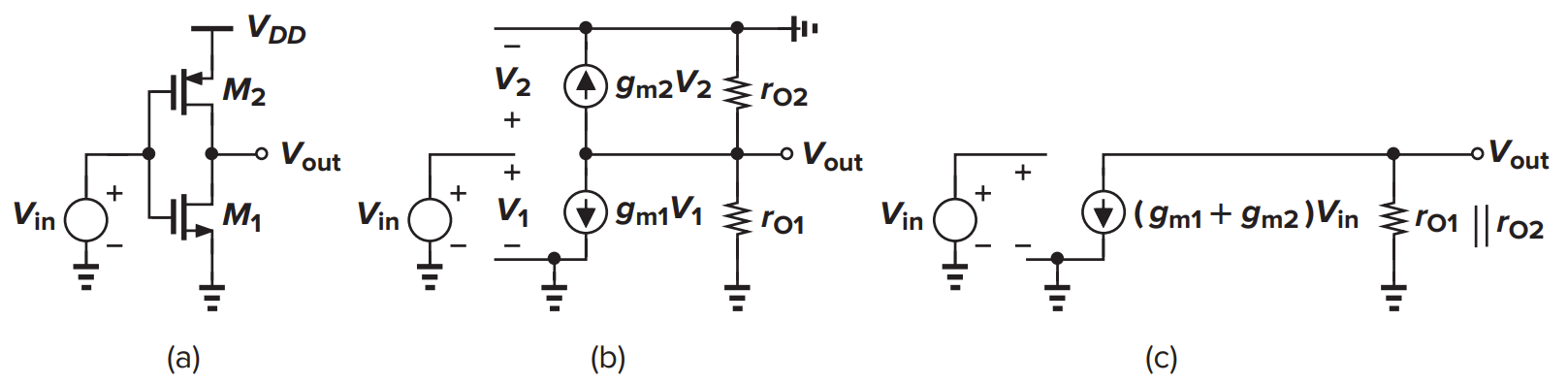
不多说，暴算

• 等效跨导 $$G_m=-g_{m1}-g_{m2}$$
• 输出阻抗 $$R_{out}=r_{o1}//r_{o2}$$
• 电压增益 $$A_{v}=-\left(g_{m1}+g_{m2}\right)\left(r_{o1} // r_{o2}\right)$$

带源衰减的共源放大器

• 如果输入信号超出输入范围，工作点可能会偏离原始/所需的直流偏置点太远，从而离开所需的饱和区域并产生失真
• 源衰减：在源和地之间插入阻抗（这是一个负反馈！）以扩展输入范围

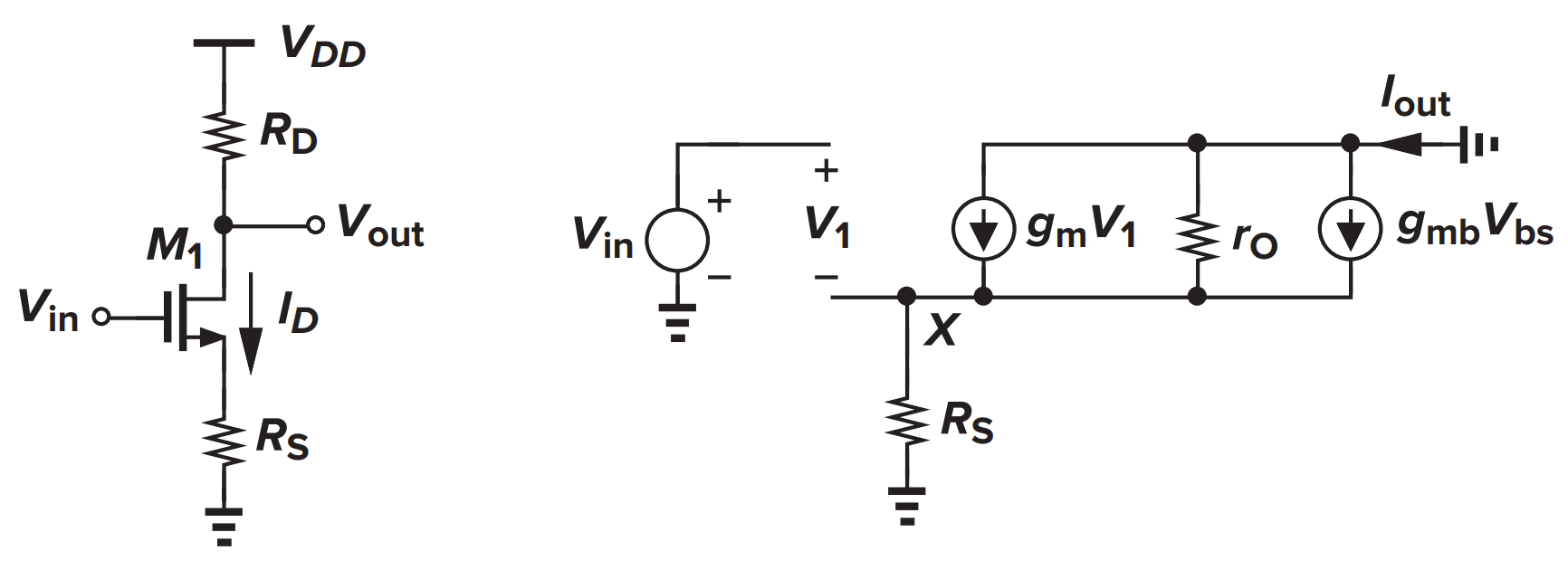
如右上图，让输出接地，计算跨导

$$G_{m}=\frac{I_{\text {out }}}{V_{\text {in }}}=\frac{-g_{m} r_{o}}{R_{S}+\left[1+\left(g_{m}+g_{m b}\right) R_{S}\right] r_{o}}$$

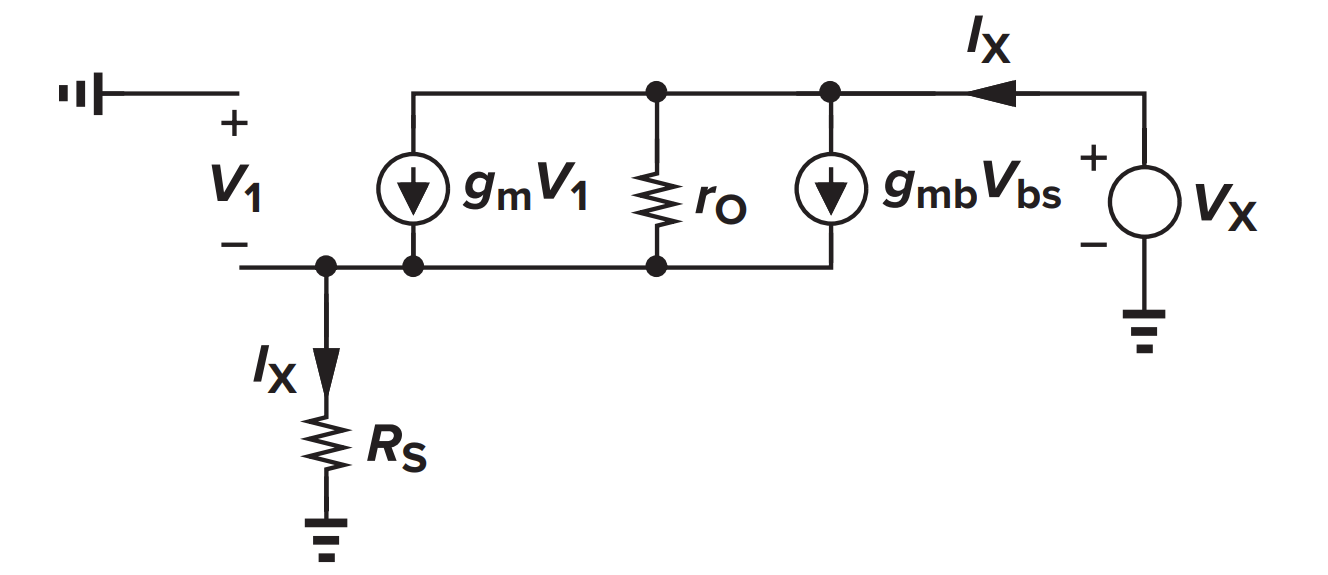
再令 $V_{in}=0$，并在输出端增加测试电压 $V_{X}$，计算输出阻抗：

$$R_{out}=r_o+R_S+(g_m+g_{mb})r_oR_S$$

于是电压增益

$$A_{v}=\frac{-g_mr_oR_D}{R_D+r_o+R_S+(g_m+g_{mb})r_oR_S}$$

共漏放大器（源跟随器）

顾名思义，CD放大器的主要作用不是放大，而且作为CS放大器的后级，用于减小输出阻抗

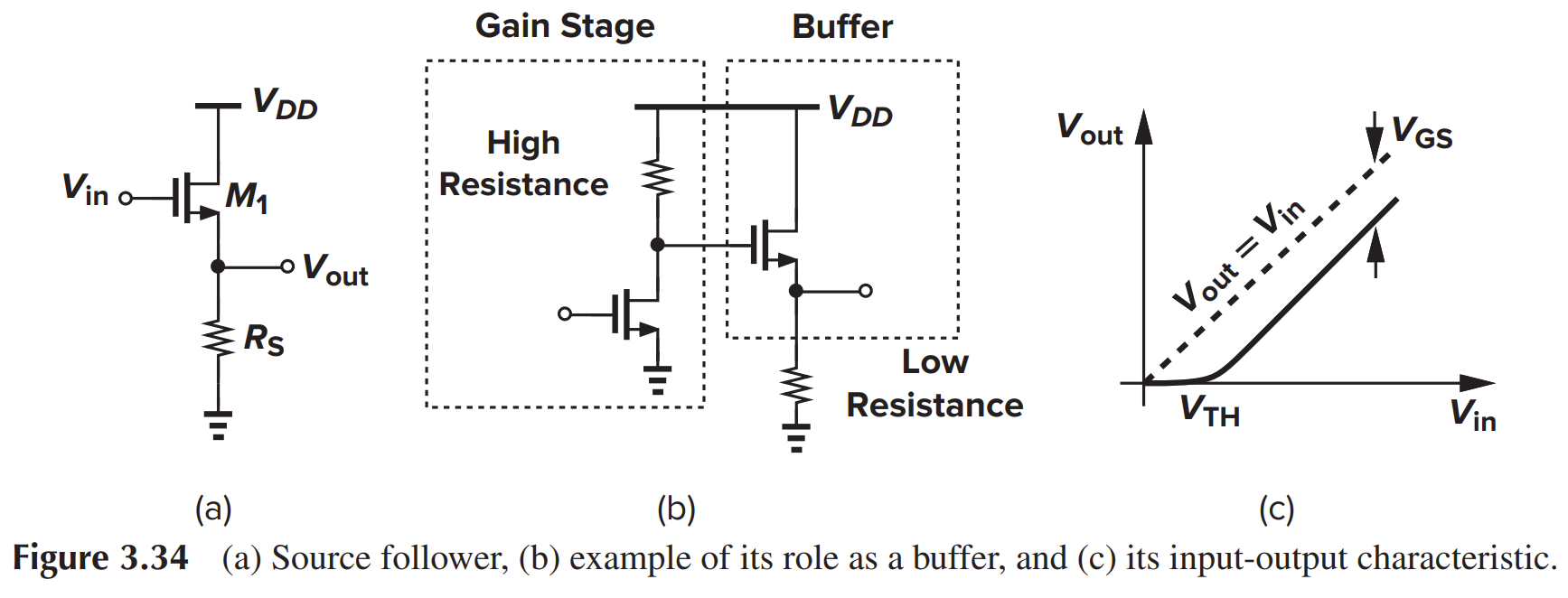
接电阻的CD/SF

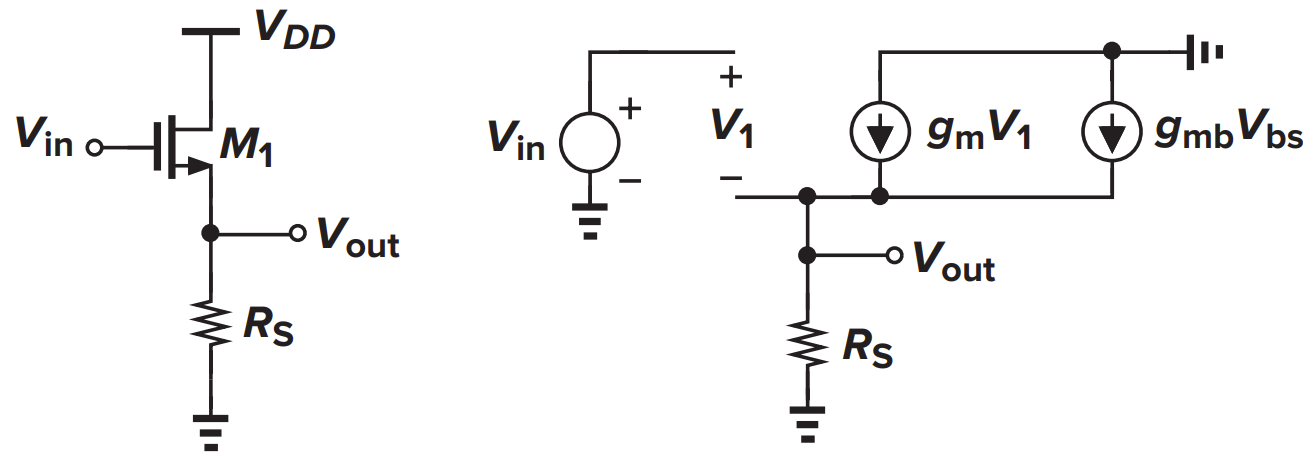
• 等效跨导 $$G_m=g_m$$
• 输出阻抗 $$R_{out}=\frac{1}{g_m+g_{mb}+1/r_0}$$
• 电压增益 $$A_{v}=\frac{g_m}{g_m+g_{mb}+1/r_0}$$

接饱和MOSFET的CD/SF

$$R_{eq}=\frac{1}{g_{mb}}//r_{o1}//r_{o2}//R_{L}$$ $$A_v=\frac{R_{eq}}{R_{eq}+\frac{1}{g_m}}$$

（？）

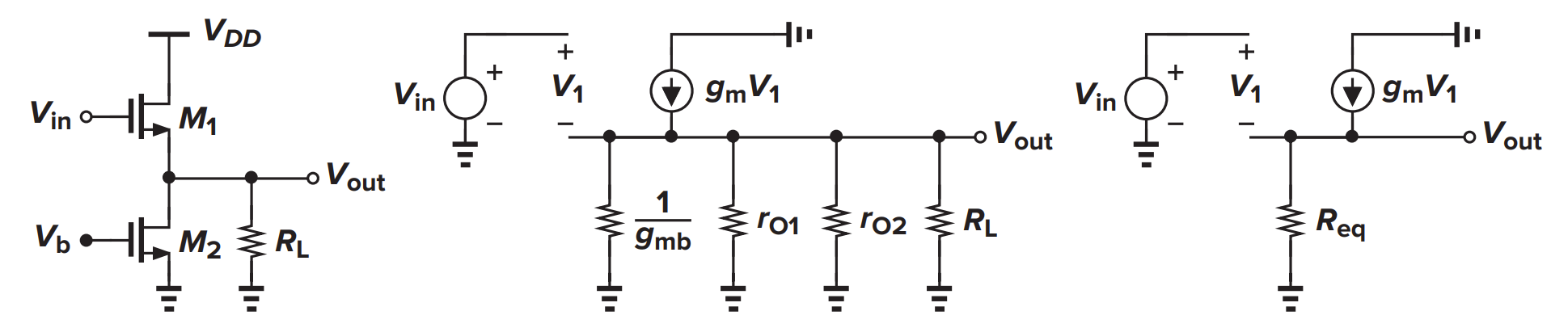
共栅放大器

• 增益是正数
• 体偏效应反而增大了增益

接电阻的共栅放大器

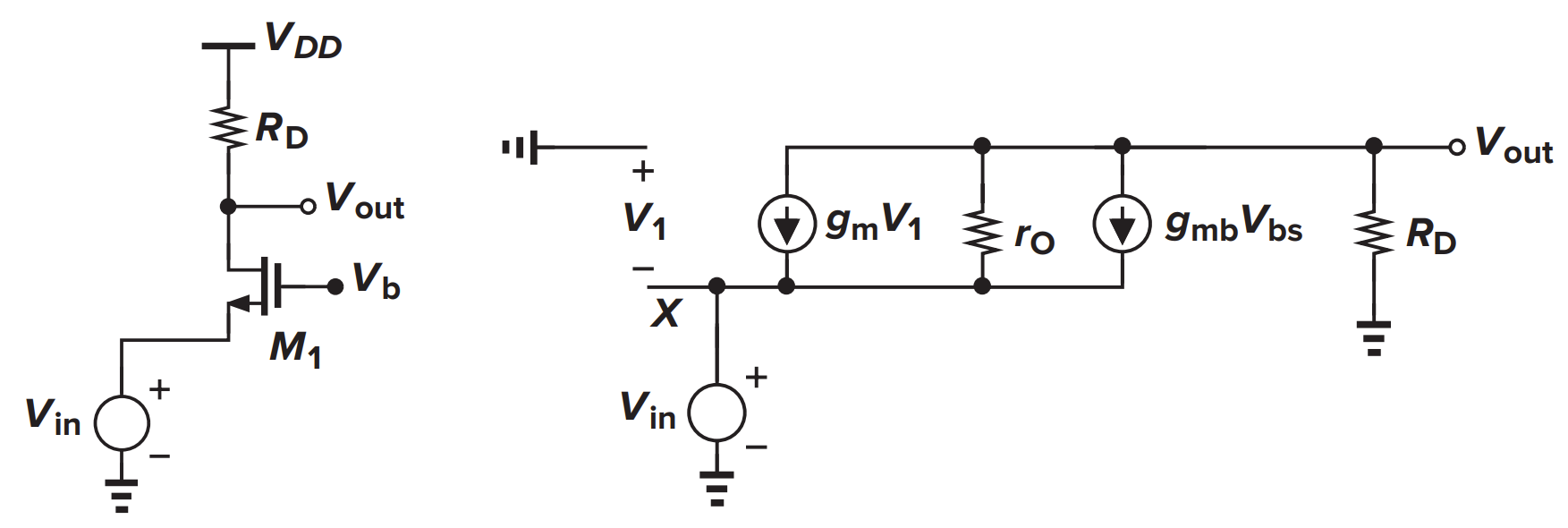
• 等效跨导 $$G_m=g_m+g_{mb}+1/r_o$$
• 输出阻抗 $$R_{out}=r_o//R_D$$
• 电压增益 $$A_{v}=\left(g_m+g_{mb}+1/r_o\right)\left(r_o//R_D\right)$$
• 输入阻抗 $$Z_{in}=\frac{1+R_D/r_o}{g_m+g_{mb}+1/r_o}$$

“漏极电阻”积木

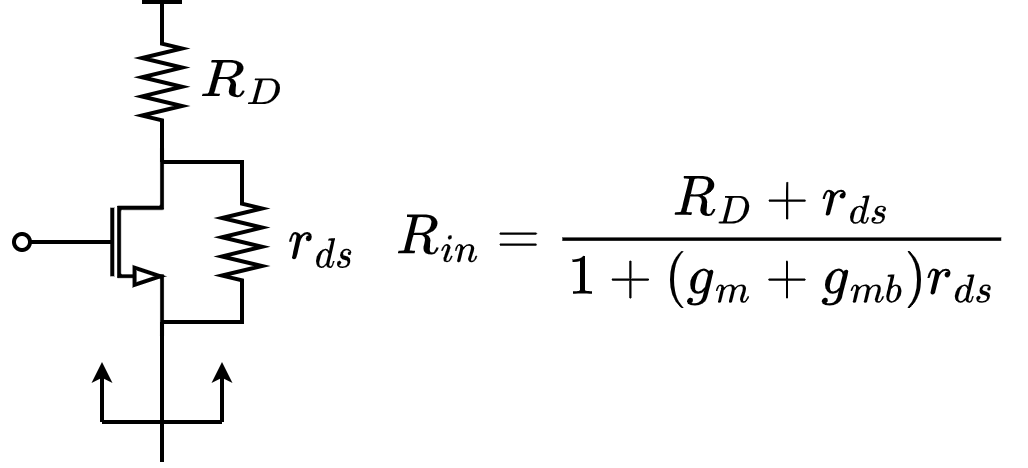
级联分析

$$\begin{array}{c} G_{m}=\frac{I_{o u t}}{V_{\text {in }}}=-g_{m 1} \frac{g_{m 2}+g_{m b}+1 / r_{o 2}}{g_{m 2}+g_{m b}+1 / r_{o 2}+1 / r_{o 1}} \approx-g_{m 1} \\ Z_{o u t}=V_{X} / I_{X}=\left(1+\left(g_{m 2}+g_{m b}\right) r_{o 2}\right) r_{o 1}+r_{o 2}=r_{o 1}+r_{o 2}+g_{m 2} r_{o 2} r_{o 1} \approx g_{m 2} r_{o 2} r_{o 1} \\ A_{v}=\frac{V_{\text {out }}}{V_{\text {in }}}=G_{m}\left(Z_{\text {out }} \| Z_{\text {load }}\right)=-g_{m 1}\left(g_{m 2} r_{o 2} r_{o 1} \| Z_{\text {load }}\right) \end{array}$$

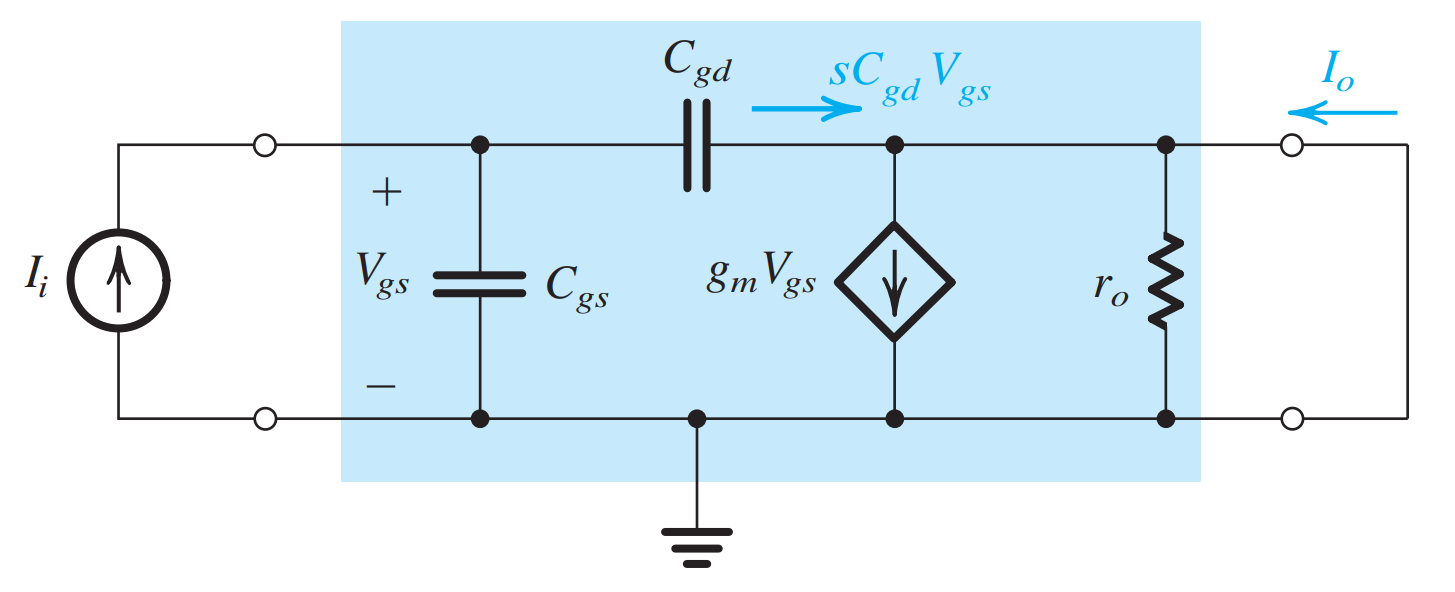
单一增益频率

单位增益频率 $f_T$，也称为过渡频率。它被定义为共源放大器的 短路 电流增益 变为 1 的频率。

$$\begin{array}{c} I_{o}=g_{m} V_{g s}-s C_{g d} V_{g s} \approx g_{m} V_{g s} \\ V_{g s}=\frac{I_{i}}{s\left(C_{g s}+C_{g d}\right)} \\ \frac{I_{o}}{I_{i}}=\frac{g_{m}}{s\left(C_{g s}+C_{g d}\right)} \\ \left|\frac{I_{o}}{I_{i}}\right|=\frac{g_{m}}{\omega\left(C_{g s}+C_{g d}\right)} \\ \omega_{T}=g_{m} /\left(C_{g s}+C_{g d}\right) \\ f_{T}=\omega_{T} / 2 \pi=\frac{g_{m}}{2 \pi\left(C_{g s}+C_{g d}\right)} \end{array}$$

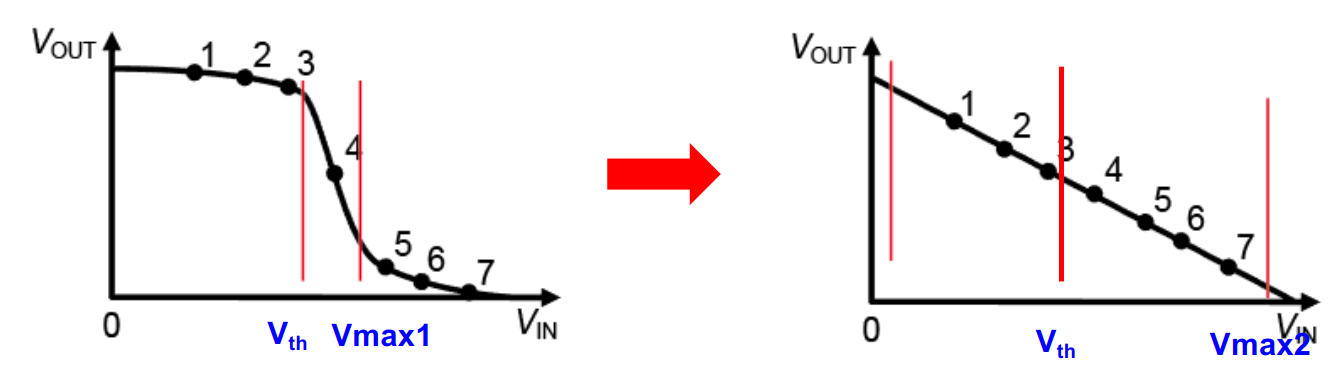
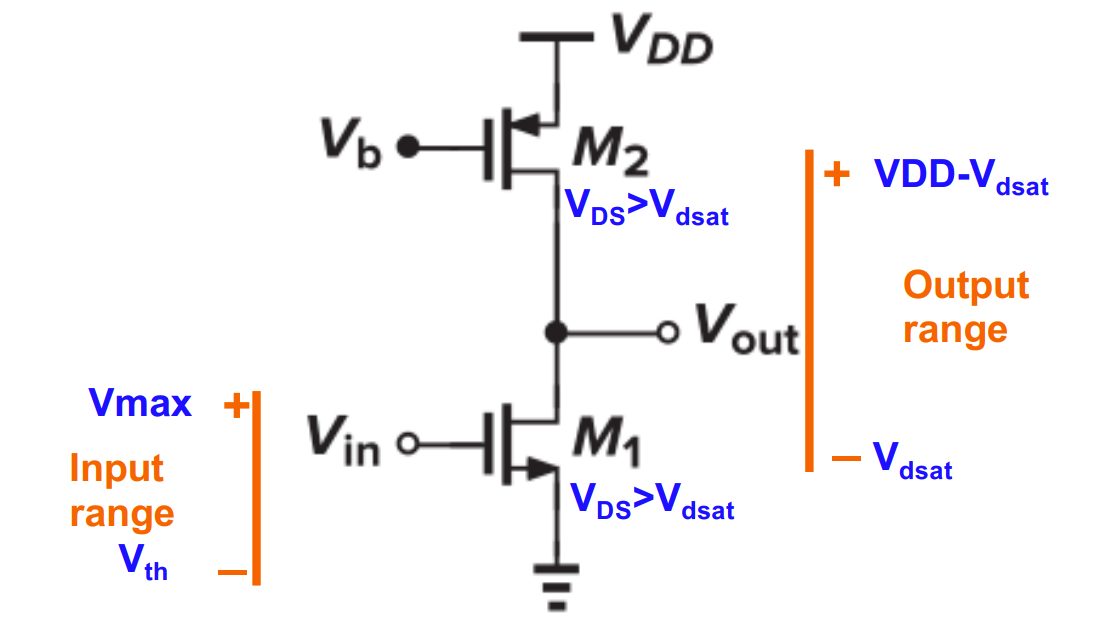
输入输出范围

• 在放大器中，放大MOSFET或MOSFET电流源需要保持在饱和区域中以获得最佳性能。
• 电压余量问题：当没有足够的电压余量来保证放大MOSFET或MOSFET电流源保持在饱和区域，通常出现在 40nm 以下制程以及 Vdd 较低时。
• 输入范围为 $V_{max}-V_{th}$，其中最小输入电压限制为 $V_{th}$，以确保 M1 保持导通，最大输入电压限制为 $V_{max}$，对应于 $V_{DS}(M1)= V_{dsat}$ 的输入电压
• 输出范围为 $V_{DD}-2*V_{dsat}$, 其中最小输入电压限制为 $V{dsat}$，以确保 $V_{DS}(M1)\ge V_{dsat}$，最大输入电压限制为 $V_{DD}-V_{dsat}$，以确保 $|V_{DS}(M2)|>=V_{dsat}$

Folded Cascode

（Todo）

差分放大器

差模信号与共模信号

$$\begin{array}{c} v_{in,CM}=\frac{v_{i+}+v_{i-}}{2}\\ v_{in,DM}=v_{i+}-v_{i-} \end{array}$$

单端放大与简单两路放大的弊端

• 电路有干扰，比如理想情况下输入信号是正弦波，但是实际情况正弦波会有“毛刺”或者“变形”
• 单端放大信号会把干扰也放大，显然不可行
• 于是考虑把信号分成正负两路，干扰也是对称的，一起被放大，那么取它们的差值，干扰就可以被去除

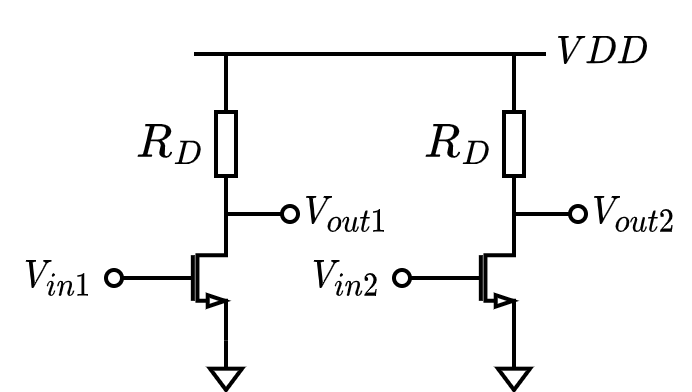
• 对于简单两路放大，如果信号的共模部分发生波动，也就相当于 DC 工作点发生变化，器件的跨导改变，小信号被放大的倍数改变。

基本差分对

为了解决上面的问题，我们使用基本差分对。

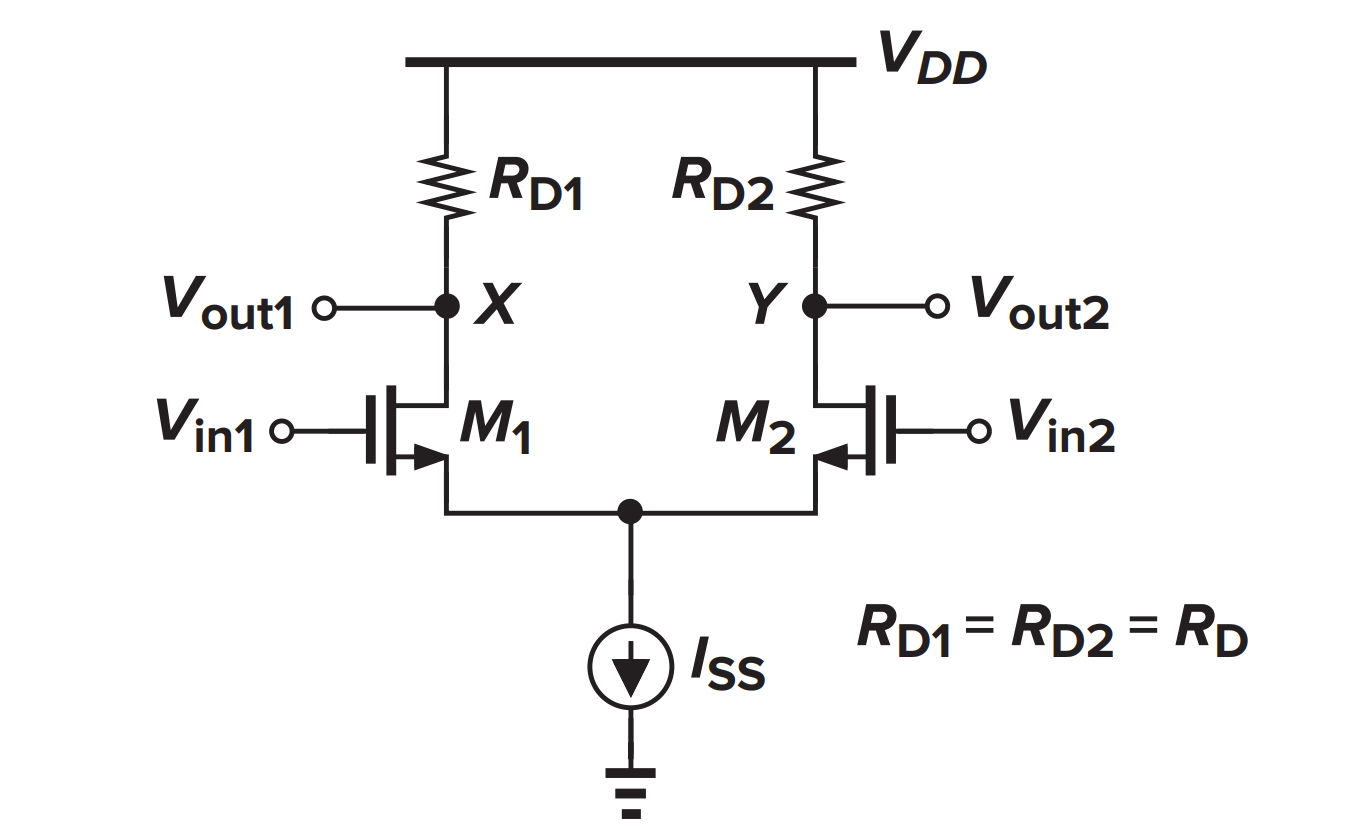
大信号分析

• 当 $V_{in1}$ 远小于 $V_{in2}$ 时，M1 关闭，M2 开启，$I_{D2}=I_{SS}$，因此 $V_{out1}=V_{DD}$，$V_{out2}=V_{DD}-R_{D}I_{SS}$
• 当 $V_{in1}$ 不断增加时，M1 开启，$I_{D1}$ 逐渐增加，但是仍然满足 $I_{D1}+I_{D2}=I_{SS}$，$V_{out1}$ 减小，$V_{out2}$ 增大
• 当 $V_{in2}$ 远小于 $V_{in1}$ 时，M2 关闭，M1 开启，$I_{D1}=I_{SS}$，因此 $V_{out1}=V_{DD}-R_{D}I_{SS}$，$V_{out2}=V_{DD}$

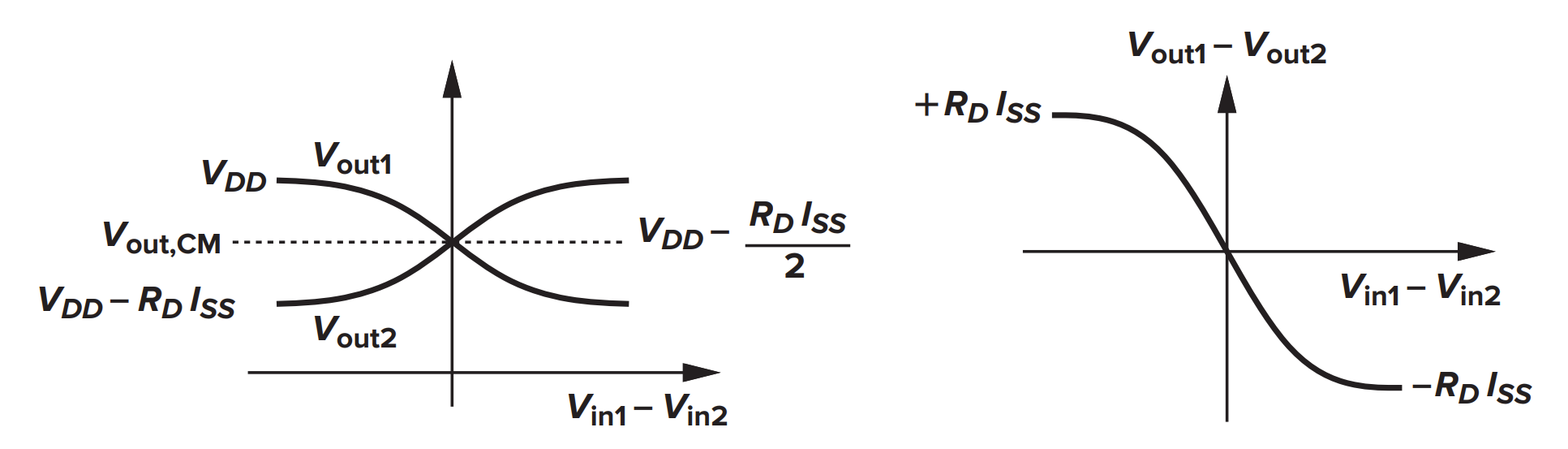
共模输入的影响

注意：共模输入 $V_{in,CM}$ 代表现实电路中可能存在的噪声，其也是交流信号！

• 当 $V_{in,CM}<V_{TH1}$，M1 和 M2 不开启，输出 $V_{DD}$，增益为 0
• 当 $V_{TH1}<V_{in,CM}<V_{GS1}+(V_{GS3}-V_{TH3})$，M1 和 M2 开启，作用是源跟随器，使得 $V_{P}$ 跟随 $V_{in,CM}$
• 当 $V_{GS1}+(V_{GS3}-V_{TH3})<V_{in,CM}$，M3 工作在饱和区，通过 M1 和 M2 的总电流不变，这是我们想要的工作区
• 当 $V_{in,CM}>\min\{V_{DD}-R_{D}I_{SS}/2+V_{TH},V_{DD}\}$，大信号特性不变，但是小信号增益下降

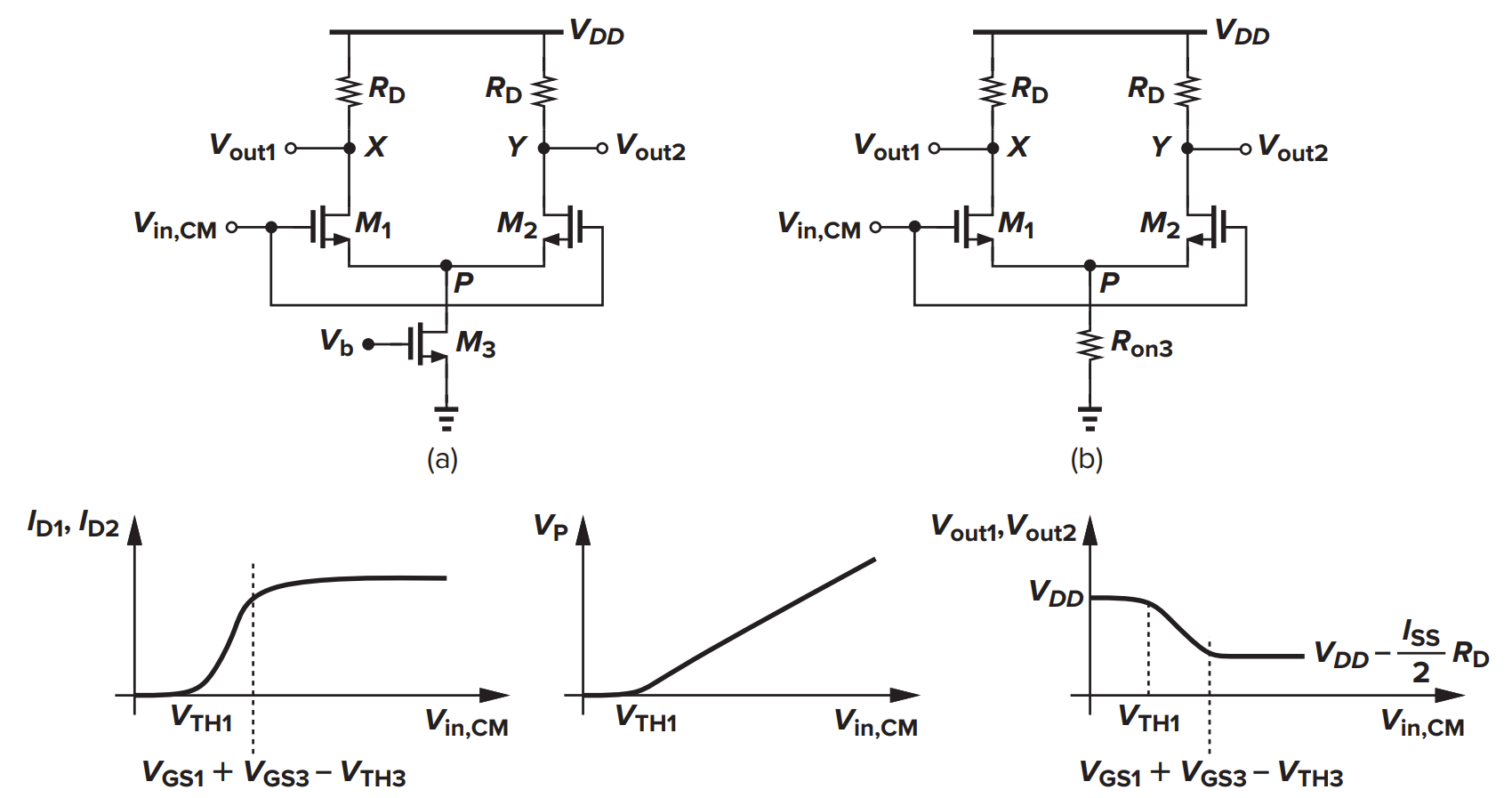
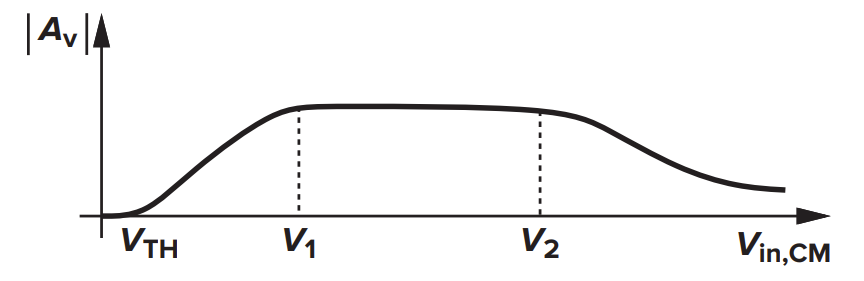
定量计算

输出电流差值

$$\begin{aligned} I_{D 1}-I_{D 2} & =\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(V_{i n 1}-V_{i n 2}\right) \sqrt{\frac{4 I_{S S}}{\mu_{n} C_{o x} \frac{W}{L}}-\left(V_{i n 1}-V_{i n 2}\right)^{2}} \\ & =\sqrt{\mu_{n} C_{o x} \frac{W}{L} I_{S S}}\left(V_{i n 1}-V_{i n 2}\right) \sqrt{1-\frac{\mu_{n} C_{o x}(W / L)}{4 I_{S S}}\left(V_{i n 1}-V_{i n 2}\right)^{2}} \end{aligned}$$

于是可以得到跨导

$$\frac{\partial \Delta I_{D}}{\partial \Delta V_{i n}}=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L} \frac{\frac{4 I_{S S}}{\mu_{n} C_{o x} W / L}-2 \Delta V_{i n}^{2}}{\sqrt{\frac{4 I_{S S}}{\mu_{n} C_{o x} W / L}-\Delta V_{i n}^{2}}}$$

当 $\Delta V_{in}=0$ 时，跨导最大，为

$$G_{m,\max}=\sqrt{\mu_{n} C_{o x} (W / L)I_{SS}}$$

电压增益

$$|A_v|=\sqrt{\mu_{n} C_{o x} (W / L)I_{SS}} R_D$$

这也满足了单源放大器的 $|A_v|=g_{m}R_{D}$

当 $\Delta V_{in}$ 太大以至于 M2 管关闭的时候，上面的分析不再成立。定义 M2 刚好关闭时的 $\Delta V_{in}$ 为 $\Delta V_{in1}$

$$\Delta V_{in1}=\sqrt{\frac{2 I_{S S}}{\mu_{n} C_{o x} W / L}}$$

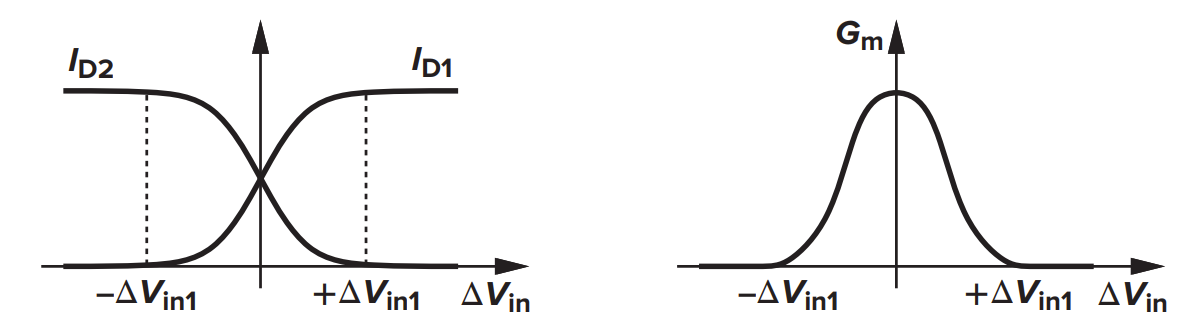
半电路小信号分析

首先，假设电路是线性的，那么左侧增加多少电流，右侧就相应减少多少电流，因此 P 点的电压是不变的，在小信号分析中可以看成“虚地”。

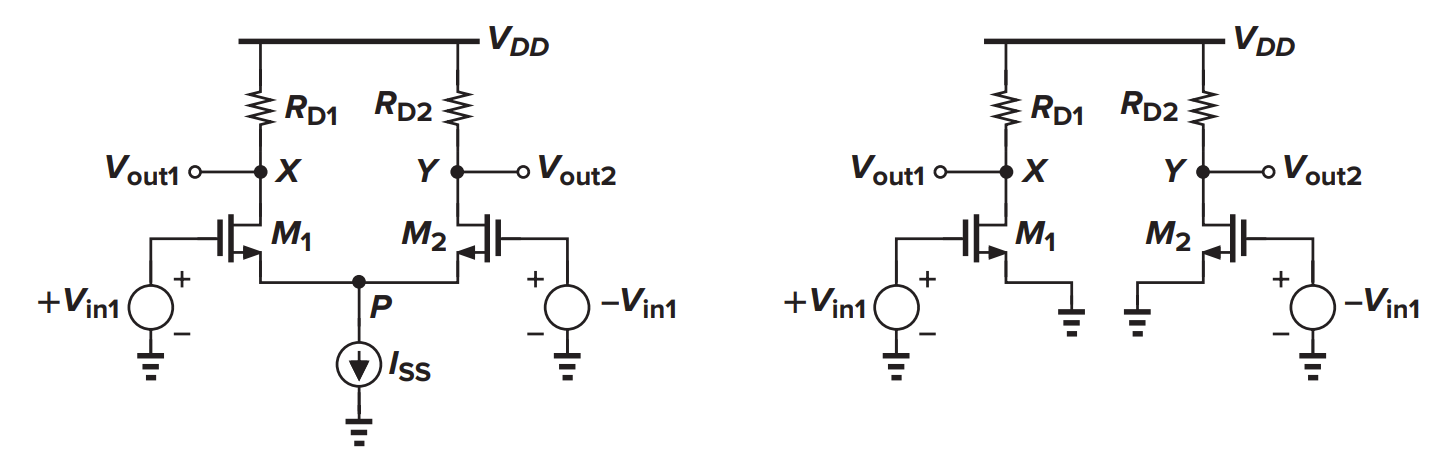
于是，差分放大器就变成了两个简单的 CS 放大器，不难得到

$$\frac{V_X-V_Y}{V_{in1}-V_{in2}}=-g_mR_D$$

源极衰减

源极衰减能提升差分放大器的线性度。定义有源极衰减时 M2 刚好关闭时的 $\Delta V_{in}$ 为 $\Delta V_{in2}$，则可得

$$\Delta V_{in2}-\Delta V_{in1}=R_SI_{SS}$$

这说明线性输入范围被扩大了 $\pm R_S I_{SS}$

而小信号增益变成了

$$|A_v|=\frac{R_D}{1/g_m+R_S}$$

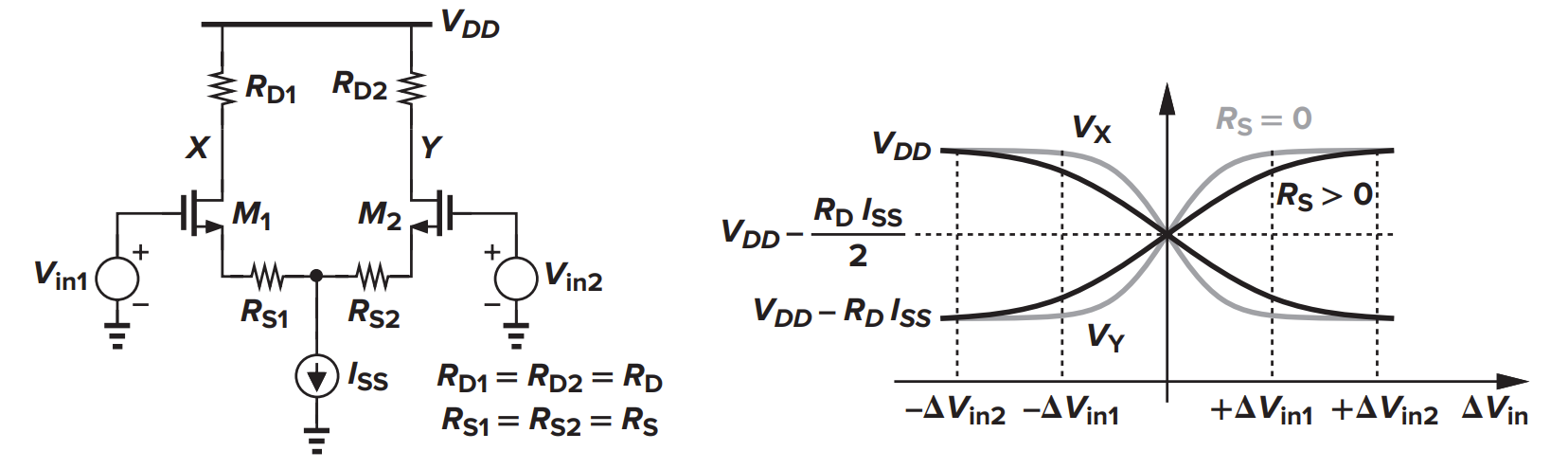
（Todo：Figure 4.28 Degenerated differential pair with split tail current source.）

共模响应（电流源有电阻）

考虑电流源 $I_{SS}$ 的输出电阻为 $R_{SS}$，那么当 $V_{in,CM}$ 变化时，P 点的电压也会变化，简单进行简化后不难发现这就是源极衰减的 CS 放大器，电压增益为

$$\begin{aligned} A_{v, C M} & =\frac{V_{\text {out }}}{V_{\text {in }, C M}} \\ & =-\frac{R_{D} / 2}{1 /\left(2 g_{m}\right)+R_{S S}} \end{aligned}$$

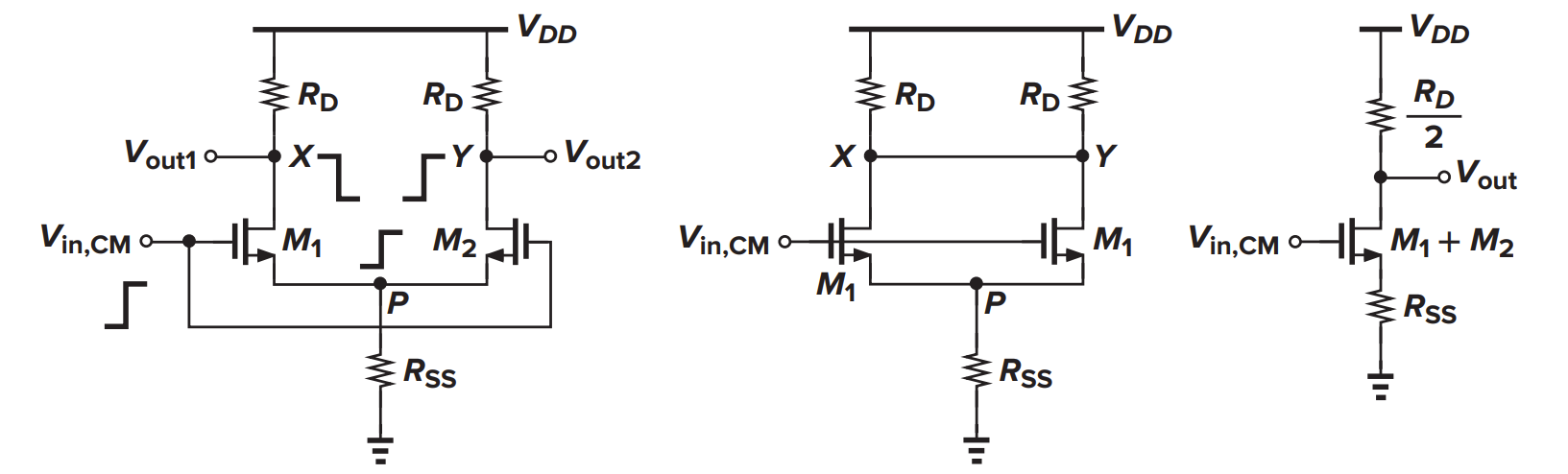
电路不对称导致的输出变化

电阻失配

假设 $R_{D1}=R_{D}$，$R_{D2}=R_{D}+\Delta R_{D}$，令 $V_{in,CM}$ 变化 $\Delta V_{in,CM}$，那么 $V_{P}$ 变化

$$\Delta V_{P}=\frac{R_{S S}}{R_{S S}+\frac{1}{2 g_{m}}} \Delta V_{i n, C M}$$

$V_{X}$ 和 $V_{Y}$ 的变化

$$\begin{array}{l} \Delta V_{X}=-\Delta V_{i n, C M} \frac{g_{m}}{1+2 g_{m} R_{S S}} R_{D} \\ \Delta V_{Y}=-\Delta V_{i n, C M} \frac{g_{m}}{1+2 g_{m} R_{S S}}\left(R_{D}+\Delta R_{D}\right) \end{array}$$

上式说明，输入端的共模变化会在输出端引入差分成分。我们称之为电路的共模到差分转换。因此，共模信号的变化会导致输出产生微小的扰动。

晶体管失配

由于尺寸和阈值电压不匹配，两个晶体管的电流略有不同，跨导也不相等。

$$\Delta (V_{X}-V_{Y})=-\frac{g_{m 1}-g_{m 2}}{\left(g_{m 1}+g_{m 2}\right) R_{S S}+1} R_{D} \Delta V_{i n, C M}$$

共模抑制比（CMRR）

定义共模抑制比（CMRR）

$$CMRR=\left|\frac{A_{v,DM}}{A_{v,CM}}\right|$$

对于理想差分放大器，CMRR 是无穷大。

• 对于电阻失配， $$CMRR = 2g_mr_s\frac{R_D}{\Delta R_D}$$
• 对于晶体管失配， $$CMRR = 2g_mr_s\frac{g_m}{\Delta g_m}$$

输入失调电压

由于适配现象的产生，当差分输入为 0 时，放大器输出也不为 0，而是输出 $V_{O}=(V_{out2}-V_{out1})$。那么反过来，使得输出为 0 的差模输入就为 $V_{OS}=V_{O}/A_{vdm}$

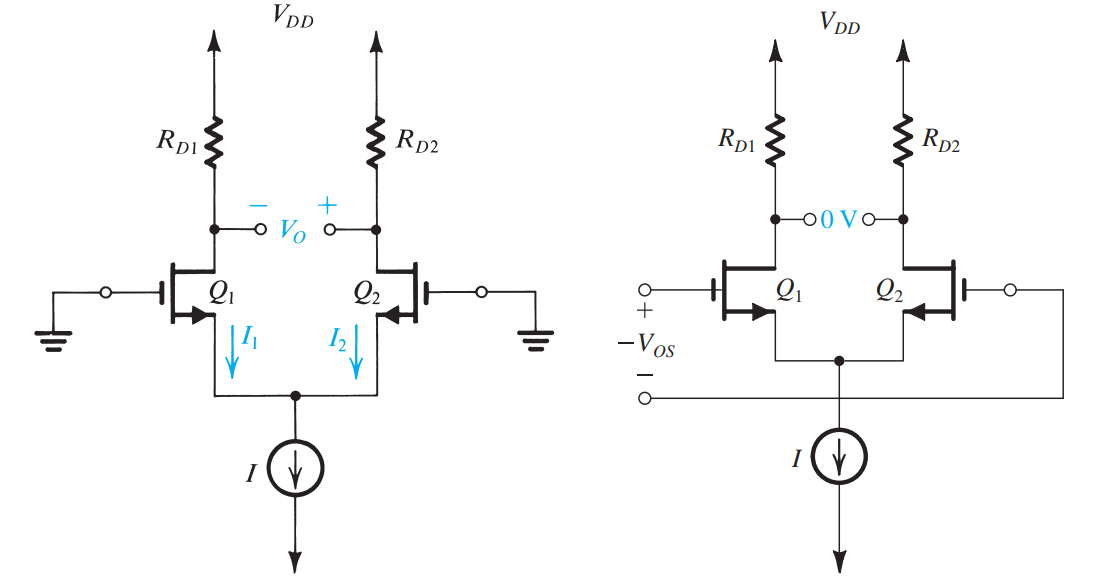
• 对于电阻失配， $$V_{OS} = \frac{V_{dsat}}{2}\frac{\Delta R_D}{R_D}$$
• 对于晶体管尺寸失配， $$V_{OS} = \frac{V_{dsat}}{2}\frac{\Delta W/L}{W/L}$$
• 对于晶体管阈值电压失配， $$V_{OS} = -\Delta V_{th}$$

总的输入失调电压：

$$V_{O S}=\sqrt{\left(\frac{V_{d s a t}}{2} \frac{\Delta R_{D}}{R_{D}}\right)^{2}+\left(\frac{V_{d s a t}}{2} \frac{\Delta(W / L)}{W / L}\right)^{2}+\left(\Delta V_{t h}\right)^{2}}$$

注意：

• 输入失调电压 和 共模抑制比 是两个不同的参数
• 输入失调电压 是大信号行为，影响小信号性能
• 共模抑制比 是小信号性能
• 输入失调电压小，共模抑制比不一定大，反之亦然

电流镜

之前提到，工作在饱和状态的 MOS 器件可以充当电流源。但是，由于沟道调制、PVT 变化等现象的存在，这个电流源其实是不太准确的。值得注意的是，即使栅极电压不是电源电压的函数，也存在工艺和温度依赖性。换句话说，如果 MOSFET 的栅极-源极电压是精确定义的，那么其漏极电流就不是！因此，我们必须寻求其他方法来偏置 MOS 电流源。

基本电流镜

我们利用这样一个事实：两个栅极电压相同、同时工作在饱和区的 MOSFET 电流相等，来制作电流镜

$$\begin{array}{l} I_{R E F} =\frac{1}{2} \mu_{n} C_{o x}\left(\frac{W}{L}\right)_{1}\left(V_{G S}-V_{T H}\right)^{2} \\ I_{\text {out }} =\frac{1}{2} \mu_{n} C_{o x}\left(\frac{W}{L}\right)_{2}\left(V_{G S}-V_{T H}\right)^{2} \end{array}$$

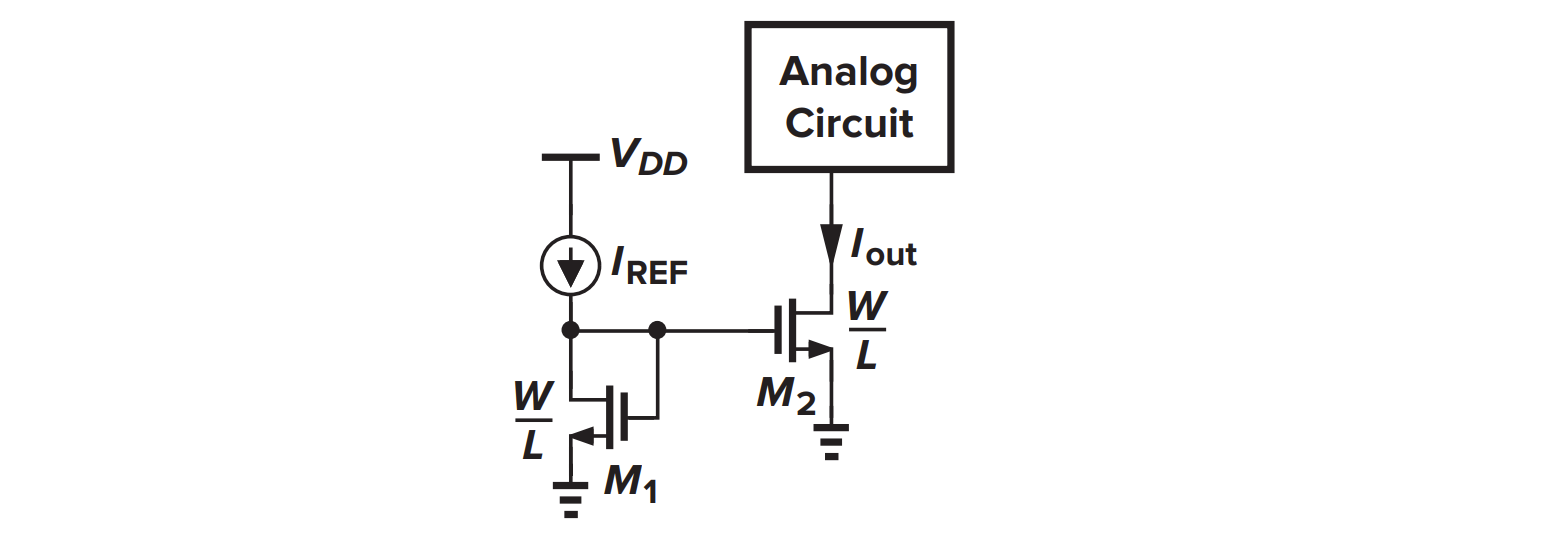
因此

$$I_{\text {out }}=\frac{(W / L)_{2}}{(W / L)_{1}} I_{R E F}$$

NMOS 电流镜能让电流流入，PMOS 电流镜能让电流流出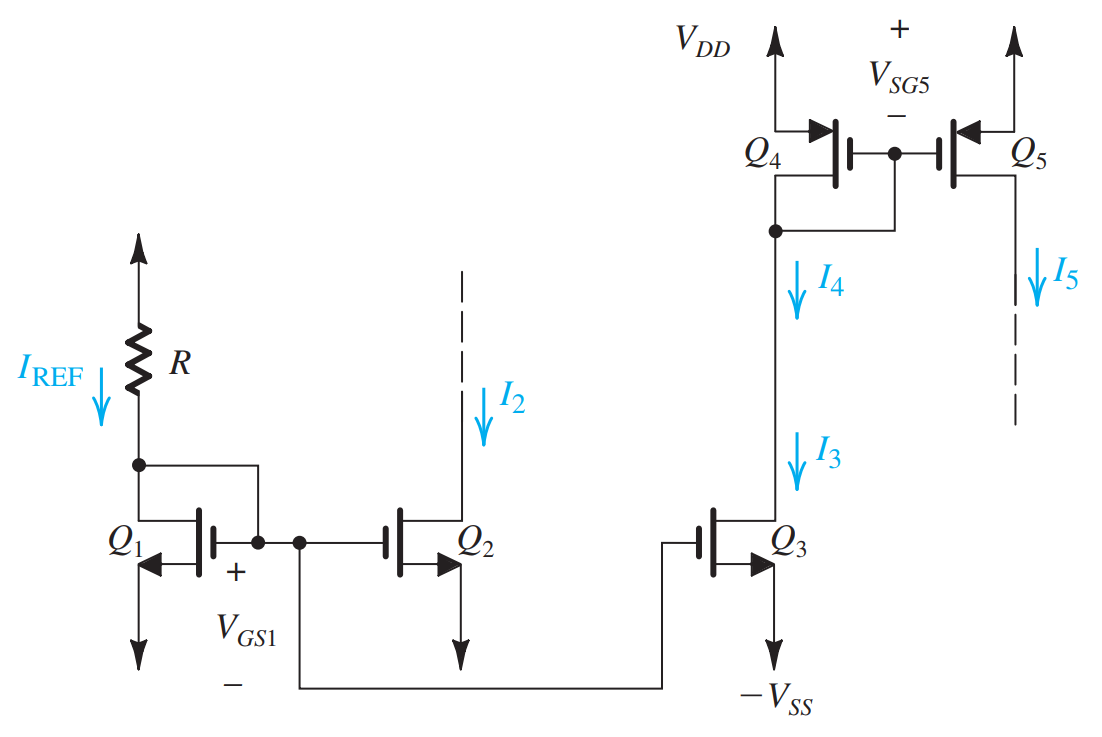

失配

尺寸失配、工艺失配

$$\frac{I_{O}}{I_{R E F}}=\frac{\mu_{n 2} C_{o x 2}\left(\frac{W}{L}\right)_{2}\left(V_{G S}-V_{t h 2}\right)^{2}\left(1+\lambda V_{D S 2}\right)}{\mu_{n 1} C_{o x 1}\left(\frac{W}{L}\right)_{1}\left(V_{G S}-V_{t h 1}\right)^{2}\left(1+\lambda V_{D S 1}\right)} \\$$

阈值电压失配

Reducing Vth mismatch effect by increasing Vdsat
at the cost of reduced output range

$$\begin{array}{l} \frac{\Delta I_{O}+I_{O}}{I_{R E F}}=\frac{\mu_{n 2} C_{o x 2}\left(\frac{W}{L}\right)_{2}\left(V_{G S}-V_{t h 1}-\Delta V_{t h}\right)^{2}\left(1+\lambda V_{D S 2}\right)}{\mu_{n 1} C_{o x 1}\left(\frac{W}{L}\right)_{1}\left(V_{G S}-V_{t h 1}\right)^{2}\left(1+\lambda V_{D S 1}\right)} \\ \frac{\Delta I_{O}}{I_{R E F}}=\frac{-2 \Delta V_{t h}}{V_{G S}-V_{t h 1}} \frac{I_{O}}{I_{R E F}} \end{array}$$

偏置失配

导致 $V_{DS}$ 的系统误差

Reducing VDS mismatch effect by increasing the output
impedance ro

源极衰减

• 提高输出阻抗 $Z_{out}=g_{m2}r_{o2}R_{S}+r_{o2}$
• 减少 $V_{DS}$ 的系统误差
• 输出电压范围减小 $I_{out}R_{S}$

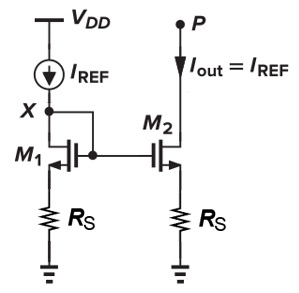
级联

为了让 $V_{DS1}=V_{DS2}$，使用级联的电流镜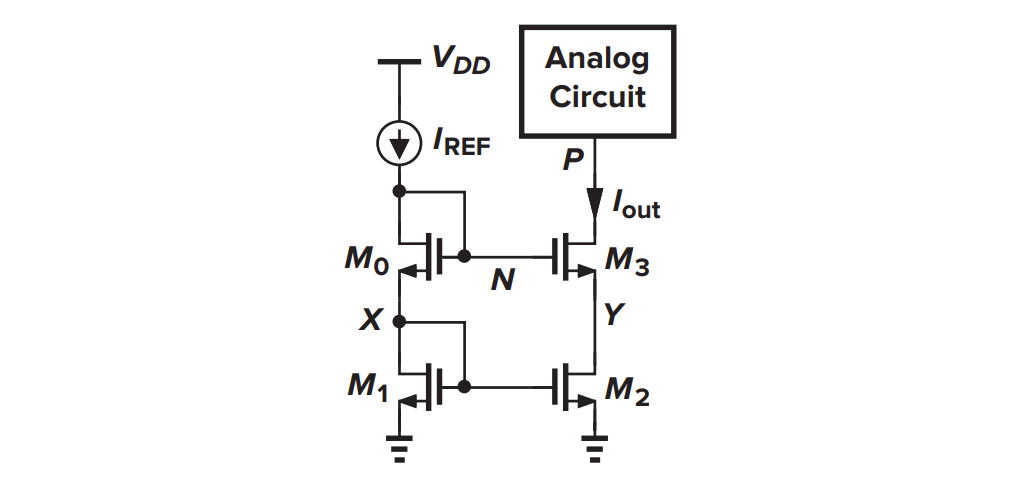

尺寸要求：$W_{3}/W_{0}=W_{2}/W_{1}$

当然，级联会让电压余度变小，

$$V_{P,\min}=(V_{GS0}-V_{TH})+(V_{GS1}-V_{TH})+V_{TH}$$

低电压级联

为了解决上面的问题，引入“低电压级联”：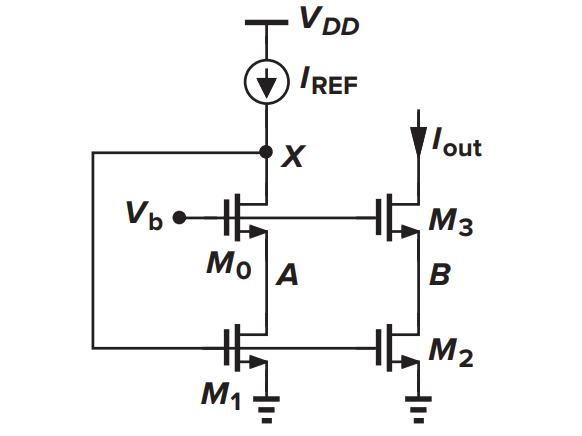

其中

$$V_{GS0}+(V_{GS1}-V_{TH1})\le V_{b}\le V_{GS1}+V_{TH0}$$

则 M0 和 M1 都工作在饱和区，就保证了 $V_{DS1}=V_{DS2}$

为了产生 $V_{b}$，使用下面的电路

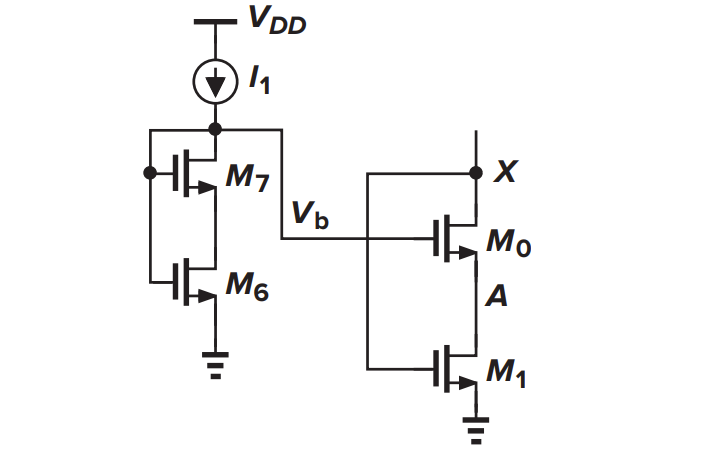
M7 饱和，M6 线性，M7 提供 $V_{GS}$，M6 提供 $V_{DS}$

Wilson 电流镜

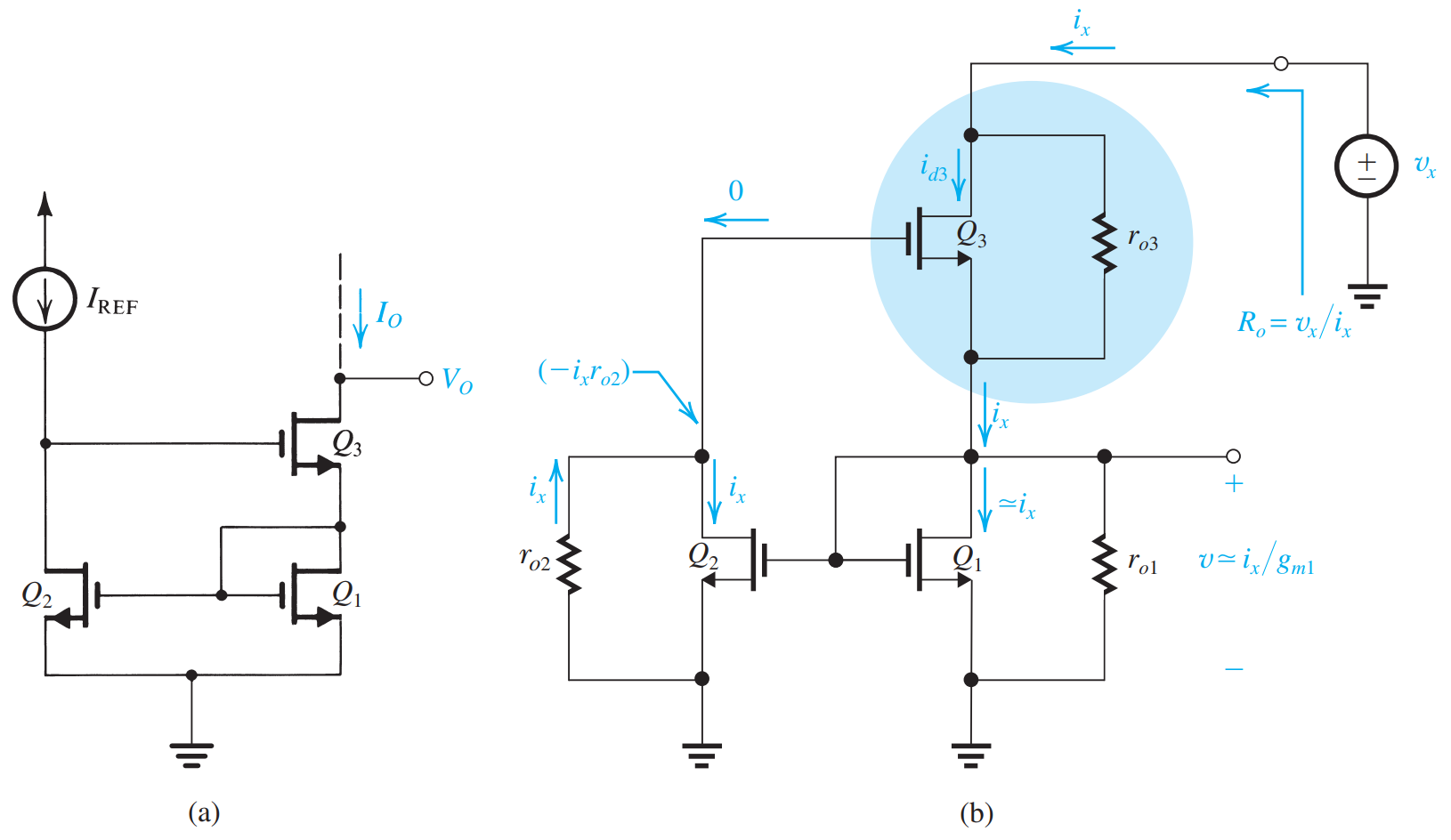
输出阻抗是

$$g_{m3} r_{o3} r_{o2}$$

gm-boosting

（Todo）

频率响应

相关概念

• 频率响应是一种线性系统分析，适用于晶体管可以通过其工作点和工作点附近的微小线性变化（即小信号分析）来充分表征的情况
• 频率响应是一种稳态分析（正弦分析），表征线性系统对各种输入信号频率的响应，包括幅值/增益响应和相位/延迟响应

传输函数

系统的输出比上输入是传输函数。

$$\begin{array}{l} H(s)=\frac{v_{o}(s)}{v_{i}(s)}=k \frac{\left(s+\omega_{Z 1}\right)\left(s+\omega_{Z 2}\right) \ldots\left(s+\omega_{Z m}\right)}{\left(s+\omega_{P 1}\right)\left(s+\omega_{P 2}\right) \ldots\left(s+\omega_{P n}\right)} \\ =a_{0} \frac{\left(1+s / \omega_{Z 1}\right)\left(1+s / \omega_{Z 2}\right) \ldots\left(1+s / \omega_{Z m}\right)}{\left(1+s / \omega_{P 1}\right)\left(1+s / \omega_{P 2}\right) \ldots\left(1+s / \omega_{P n}\right)} \end{array}$$

其中：

• $\left(-\omega_{Z m}\right)$ 是系统的零点
• $\left(-\omega_{P n}\right)$ 是系统的极点
• $a_{0}$ 是 DC 增益
• $|H(j\omega)|$ 是频率响应
• $\varphi(\omega)$ 是相位响应

-3dB 截止频率

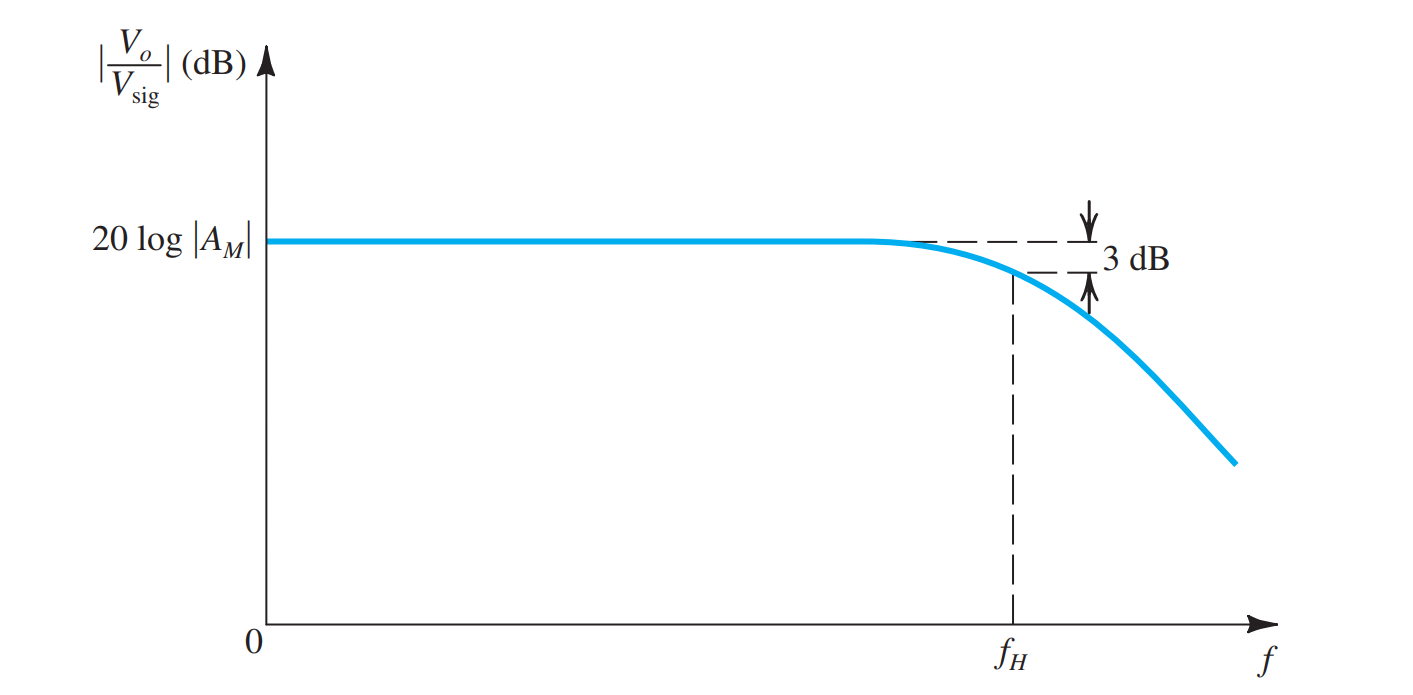
以 20dB 对数坐标画出频率响应图，

• -3dB 频率：又称角频率或截止频率，与最大幅度/增益相比，该频率的幅度/增益下降 3dB
• 带宽：又称 -3dB 带宽，带通情况下两个 -3dB 频率之间的距离，或低通情况下 -3dB 频率与直流之间的距离

RC 传输线极点

$$H(s)=\frac{V_{o}(s)}{V_{i}(s)}=\frac{\frac{1}{s C}}{R+\frac{1}{s C}}=\frac{1}{1+s R C}$$

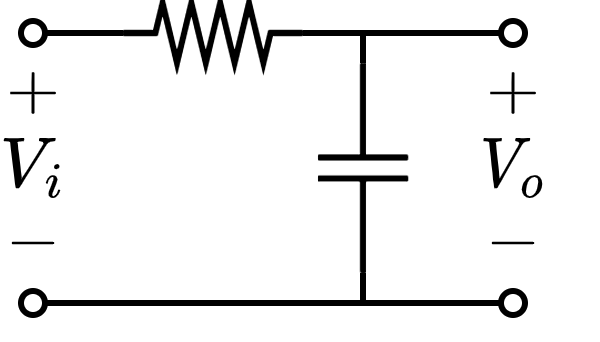
极点

$$\omega_p=-\frac{1}{RC}$$

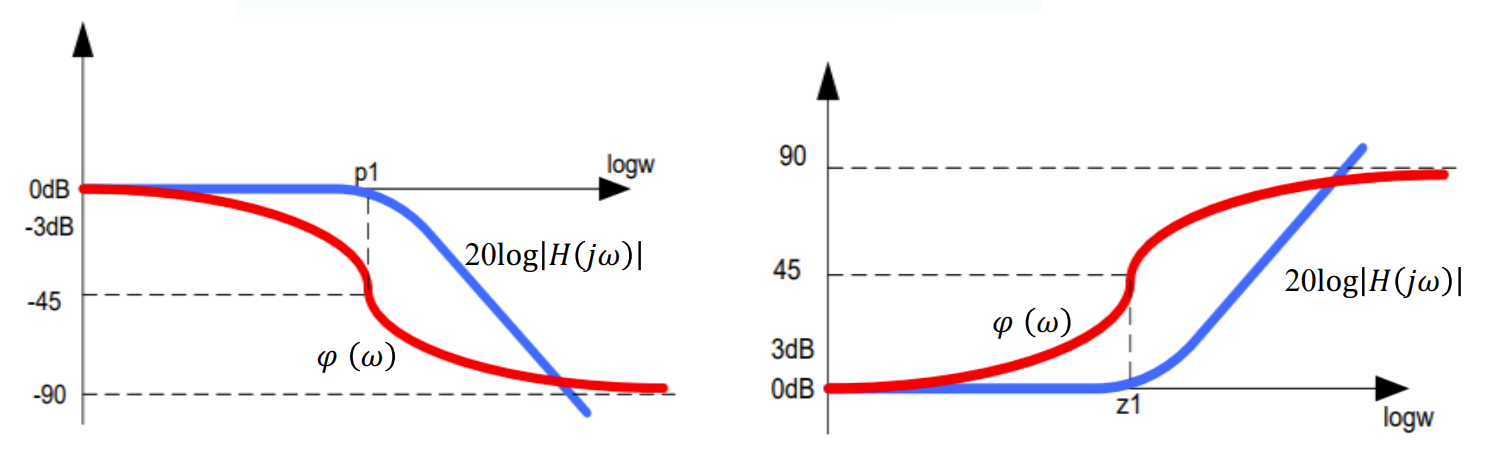
波特图

• For magnitude response
  • A real pole contributes -20dB/dec
  • A real zero contributes 20dB/dec
• For phase response (and stability)
  • A LHP real pole contributes -90° (reducing gain and reducing phase)
  • A RHP real pole contributes +90° (unstable with growing amplitude)
  • A LHP real zero contributes +90° (increasing gain and increasing phase)
  • A RHP real zero contributes -90° (increasing gain and reducing phase, potentially unstable in a closed-loop feedback system)

米勒近似

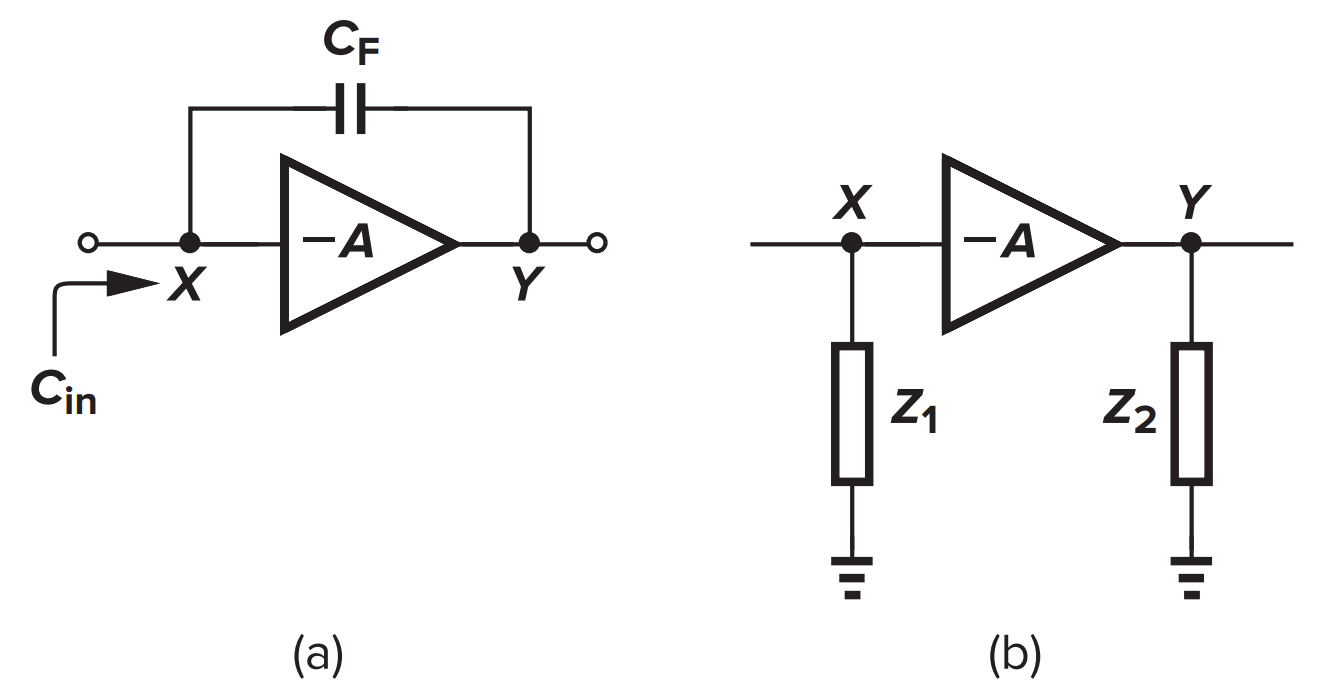
当放大器输入输出两端之间存在一个电容时，可以将其等效为两个对地的电容，大小为

$$\begin{array}{c} Z_1=\frac{1}{sC_F(1+A)}\\ Z_2=\frac{1}{sC_F(1+1/A)}\approx \frac{1}{sC_F}\\ \end{array}$$

• 米勒近似对于高频输出极点估计可能不准确
• 米勒近似可能丢失零点

CS 放大器极点分析

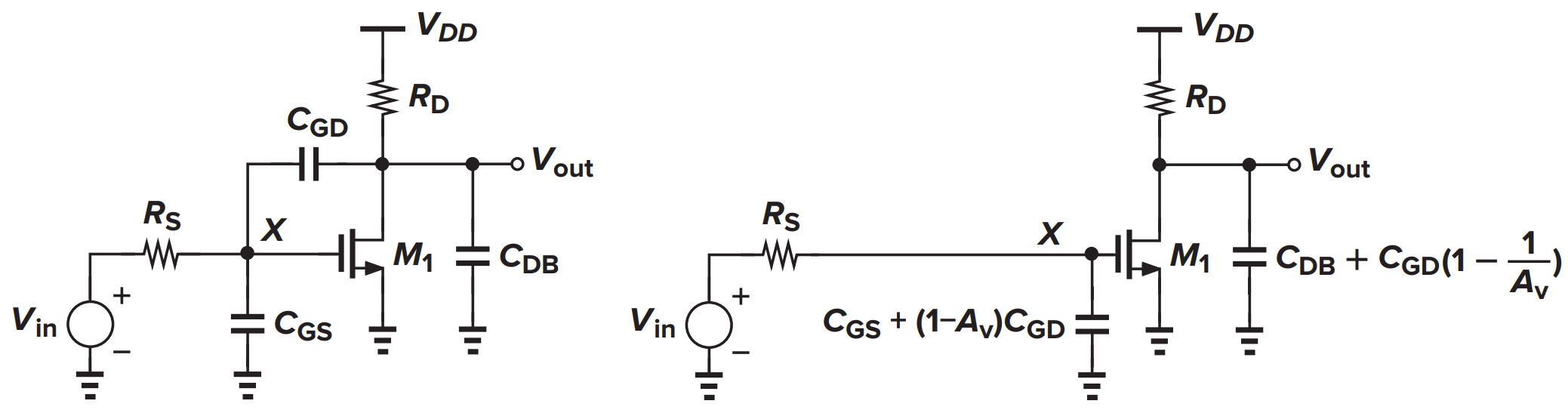
输入和输出的极点：

$$\begin{array}{c} \omega_{i n}=\frac{1}{R_{S}\left[C_{G S}+\left(1+g_{m} R_{D}\right) C_{G D}\right]} \\ \omega_{\text {out }}=\frac{1}{R_{D}\left(C_{D B}+C_{G D}\right)} \end{array}$$

CS 放大器零点分析

不能用米勒近似

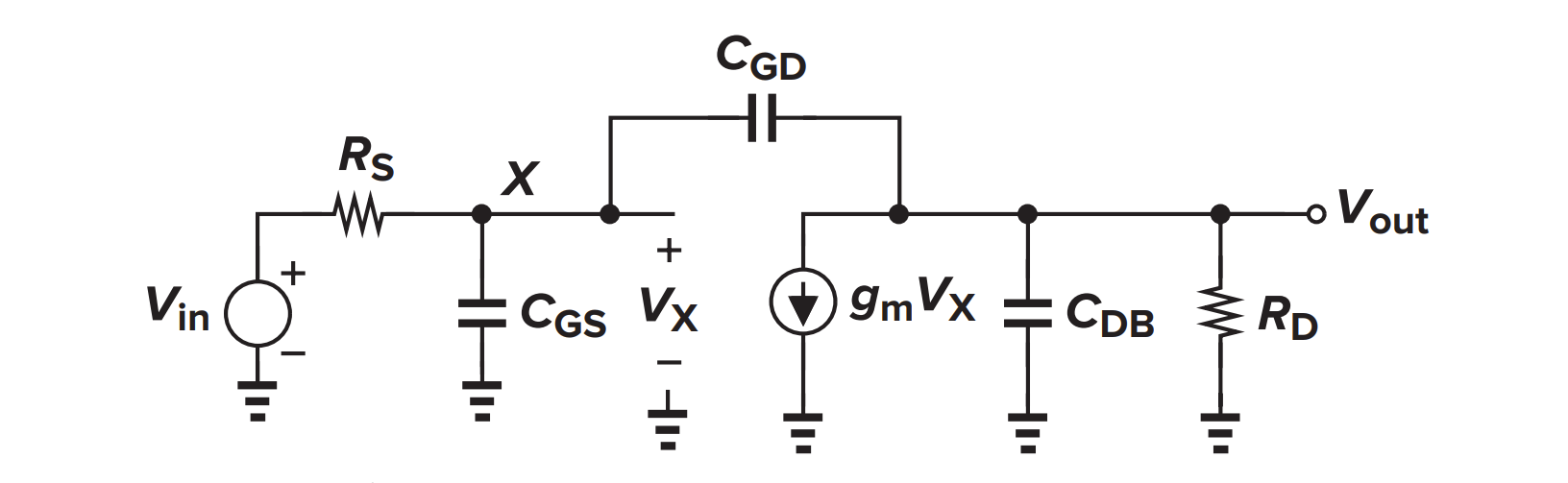
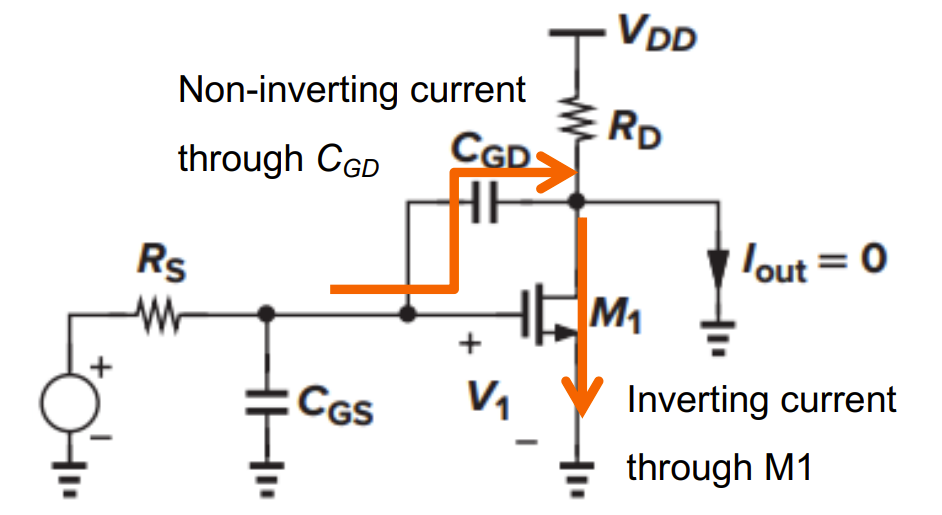
分析零点时，可以把输出点接地，写出 KCL 方程：

$$V_1C_{GD}s_z=g_mV_1$$

Cascode 放大器极点分析

• 级联级抑制了米勒效应，提高了共源 (CS) 级的带宽
• 级联结构的另一个优点是，它的主极点通常位于输出端：负载电容实际上有助于提高稳定性。

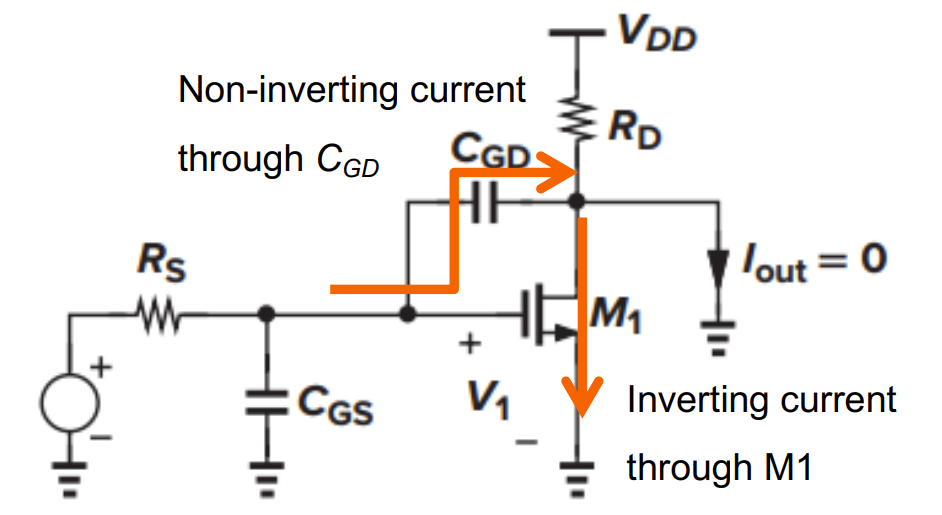
输入端，A 点到 X 点的增益 $G_m$ 是 $g_{m1}$，而 $R_{out}=\frac{1}{g_{m2}+g_{mb2}}$，故本征增益 $A=-\frac{g_{m1}}{g_{m2}+g_{mb2}}$，由米勒近似，A 点对地电容可以计算。

$$\begin{array}{c} \omega_{p, A}=\frac{1}{R_{S}\left[C_{G S 1}+\left(1+\frac{g_{m 1}}{g_{m 2}+g_{m b 2}}\right) C_{G D 1}\right]} \\ \omega_{p, X}=\frac{g_{m 2}+g_{m b 2}}{2 C_{G D 1}+C_{D B 1}+C_{S B 2}+C_{G S 2}} \\ \omega_{p, Y}=\frac{1}{R_{D}\left(C_{D B 2}+C_{L}+C_{G D 2}\right)} \end{array}$$

Source Follower 零极点分析

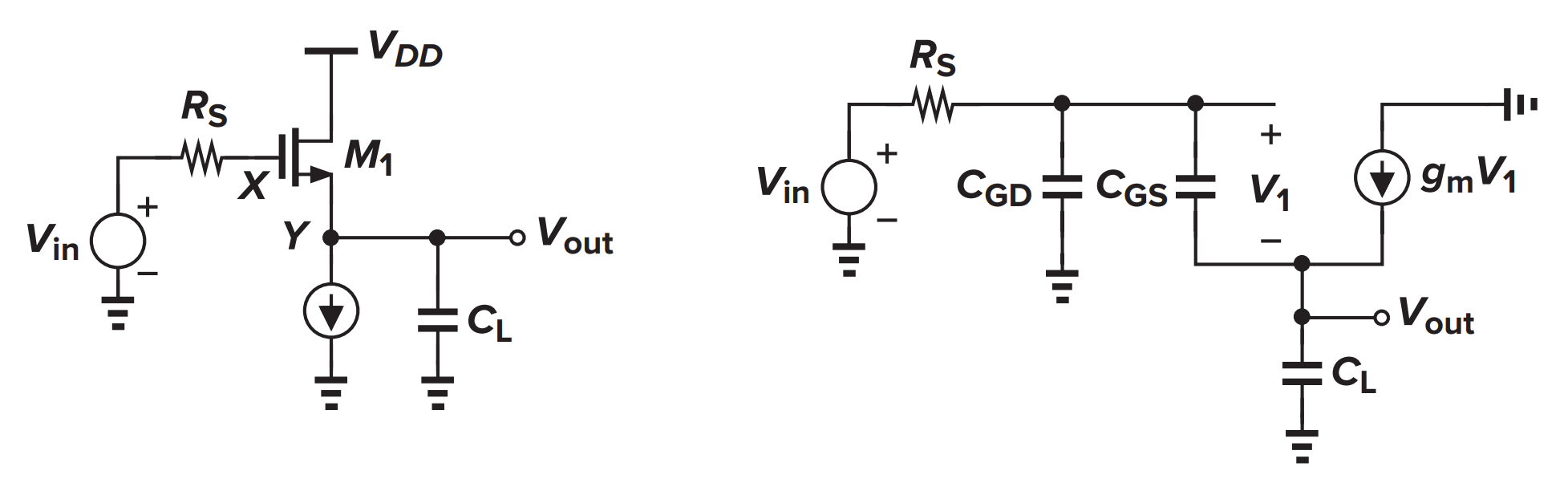
• 放大器倍数 $A$ 近似等于 1，故米勒近似的系数为 0，X 点极点为： $$\omega_{p, X} \approx \frac{1}{R_{S} C_{G D}}$$
• 如果 $R_{S}$ 很小， $$\omega_{p, Y} \approx \frac{1}{C_{L} / g_{m}+C_{G S} / g_{m}}$$ 如果 $R_{S}$ 很大， $$\omega_{p, Y} \approx \frac{g_{m}}{C_{L}+C_{G s} C_{G D} /\left(C_{G s}+C_{G D}\right)}$$ 零点： $$s_ZC_{GS}V_1=-g_mV_1 \Rightarrow s_{Z}=-\frac{g_m}{C_{GS}}$$

Common-Gate 放大器极点分析

Compared to CS, CG has higher bandwidth since the resistance and capacitance at the input node are smaller

$$\begin{array}{c} \omega_{\text {in }}=\frac{g_{m}+g_{m b}+R_{S}^{-1}}{C_{S}}\\ \omega_{\text {out }}=\frac{1}{R_{D} C_{D}} \end{array}$$

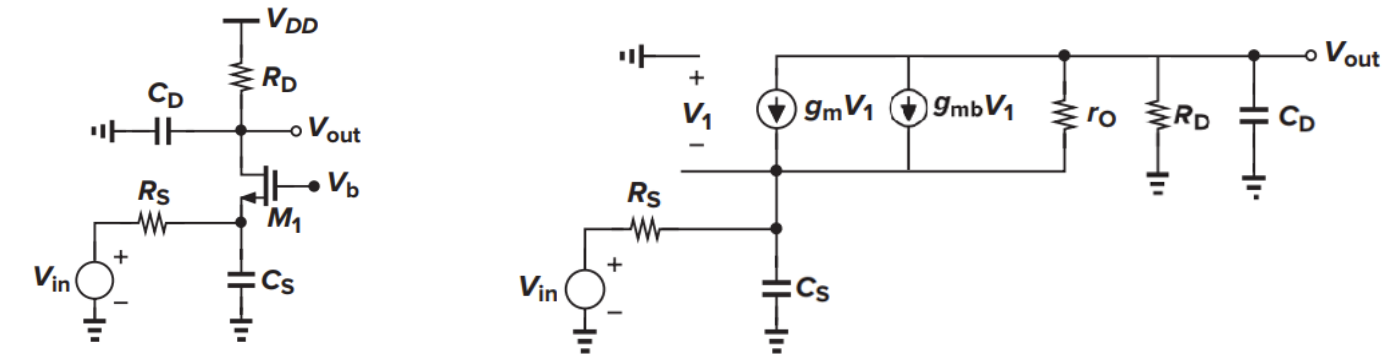
Diff Pair With Passive Load 分析

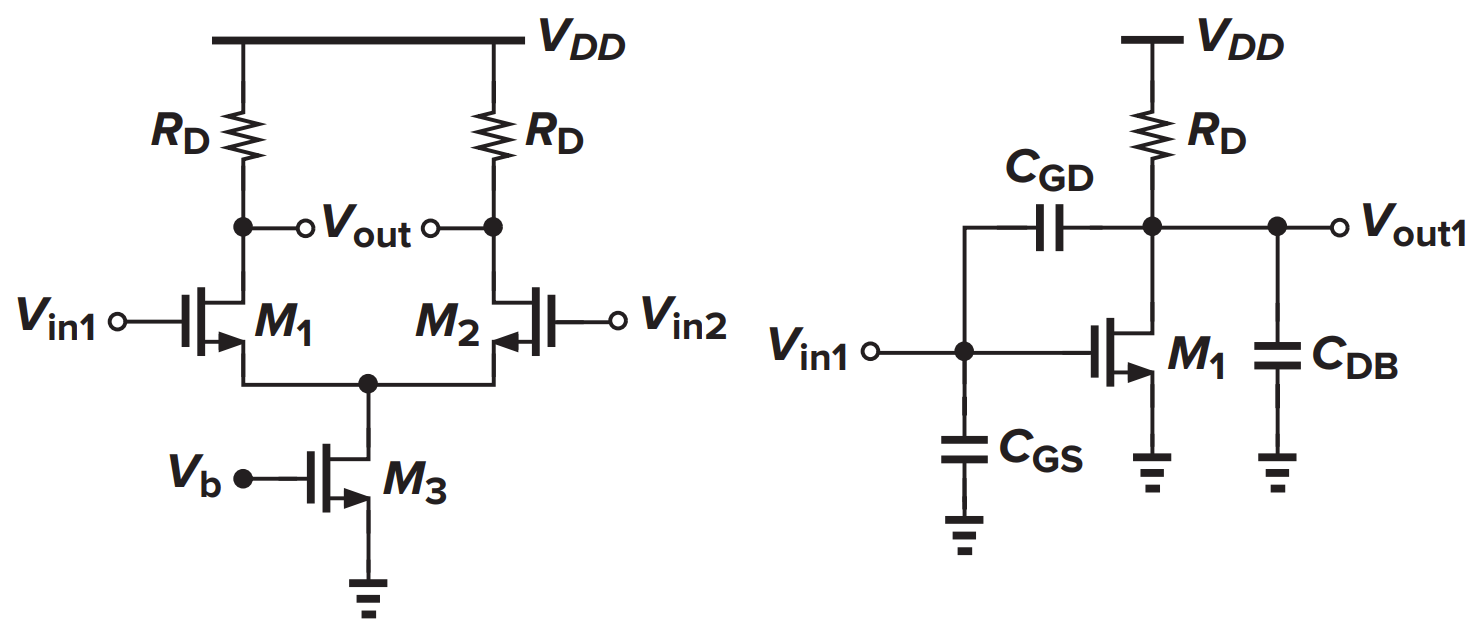
极点

$$\begin{array}{c} \omega_{\text {in }} =\frac{1}{R_{S}\left[C_{G S}+\left(1+g_{m} R_{D}\right) C_{G D}\right]} \\ \omega_{\text {out }} \approx \frac{1}{R_{D}\left(C_{D B}+C_{G D}\right)} \\ \end{array}$$

零点

$$s_{Z} =+\frac{g_{m}}{C_{G D}}$$

Diff Pair With Active Load 分析

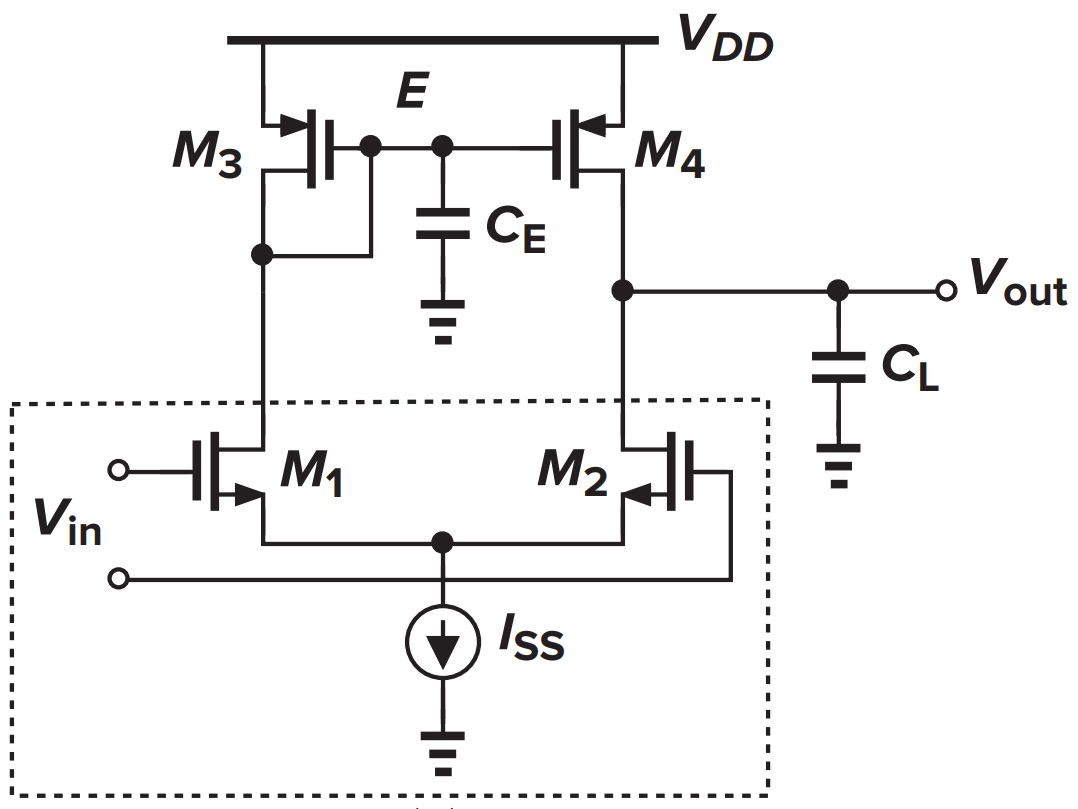
信号路径 1 (M1-M3-M4): 2 poles

$$\begin{array}{c} \omega_{p, E} \approx \frac{g_{m 3}}{C_{E}} \\ \omega_{p, \text { out }} \approx \frac{1}{\left(r_{O N} \| r_{O P}\right) C_{L}} \\ \end{array}$$

信号路径 2 (M2): 1 pole

$$\omega_{p, \text { out }} \approx \frac{1}{\left(r_{O N} \| r_{O P}\right) C_{L}}$$

相加得到传输函数

$$\begin{aligned} \frac{V_{\text {out }}}{V_{\text {in }}}&=\frac{g_{m 1}\left(r_{O N} \| r_{O P}\right) / 2}{\left(1+s\left(r_{O N} \| r_{O P}\right) C_{L}\right)}+\frac{g_{m 1}\left(r_{O N} \| r_{O P}\right) / 2}{\left(1+s \frac{C_{E}}{g_{m 3}}\right)\left(1+s\left(r_{O N} \| r_{O P}\right) C_{L}\right)} \\ &=\frac{g_{m 1}\left(r_{O N} \| r_{O P}\right)}{\left(1+s\left(r_{O N} \| r_{O P}\right) C_{L}\right)} \frac{1+s \frac{C_{E}}{2 g_{m 3}}}{\left(1+s \frac{C_{E}}{g_{m 3}}\right)} \\ \end{aligned}$$

可得零点

$$s_{Z}=-\frac{2 g_{m 3}}{C_{E}}$$

GBW

$$\text{GBW}=A_0\omega_{-3\mathrm{dB}}/2\pi=\omega_{u}/2\pi$$

运算放大器

理想运放

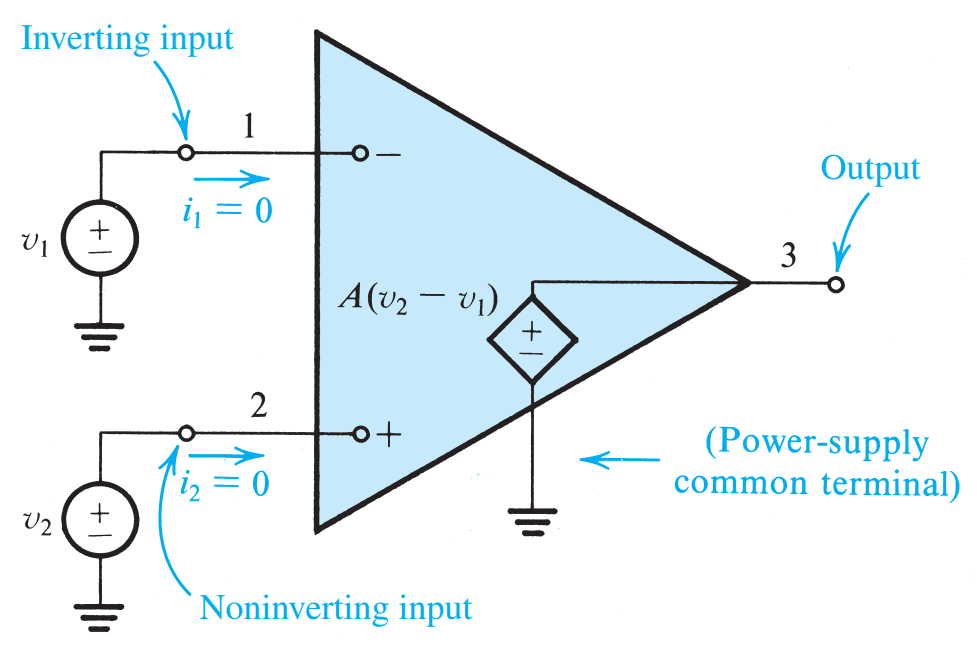
• Infinite voltage gain (practically >60dB)
• Infinite bandwidth
• Infinite slew rate
• Infinite input impedance
• Infinite CMRR
• Infinite output voltage & current range
• Zero output impedance
• Zero input offset
• Zero noise
• Zero distortion
• Zero power

开环与闭环

Open-loop amplifiers

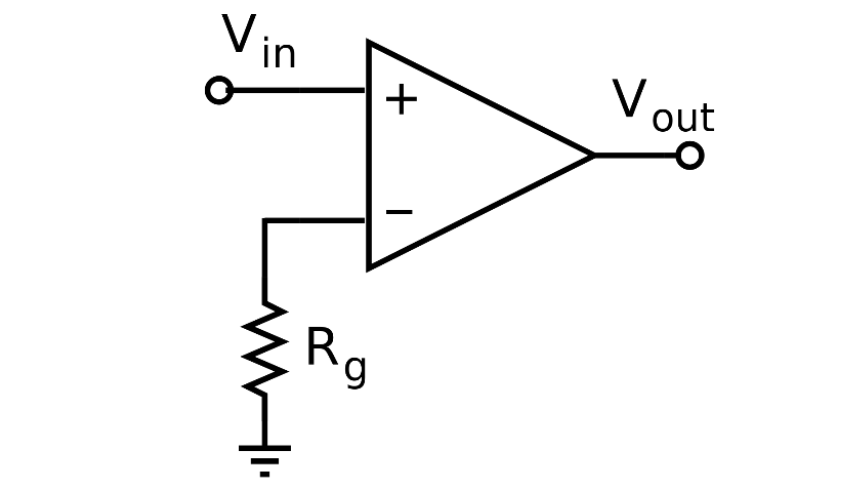
• Since the opamp gain is very high, any difference between the two input terminals (“+” and “-”) would drive the opamp into clipping or saturation
• The open-loop opamp acts as a comparator, not a linear amplifier

Closed-loop amplifiers

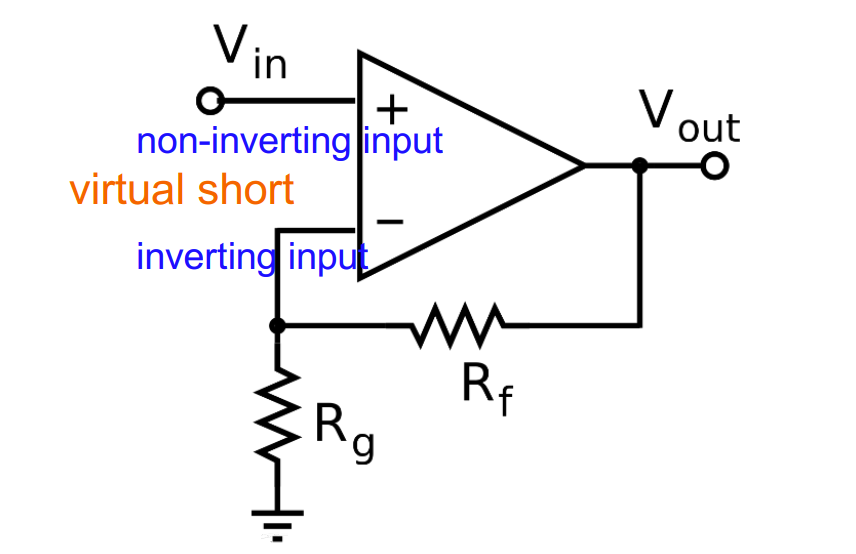
• If predictable operation is desired, negative feedback is employed by applying a portion of the output voltage to the inverting input.
• As long as the opamp gain is high enough, the characteristics of the closed-loop amplifier, such as the gain, input and output impedance, bandwidth etc., are determined by external linear components (usually resistors and capacitors) and have little dependence on non-ideal effects in the opamp itself

基本架构

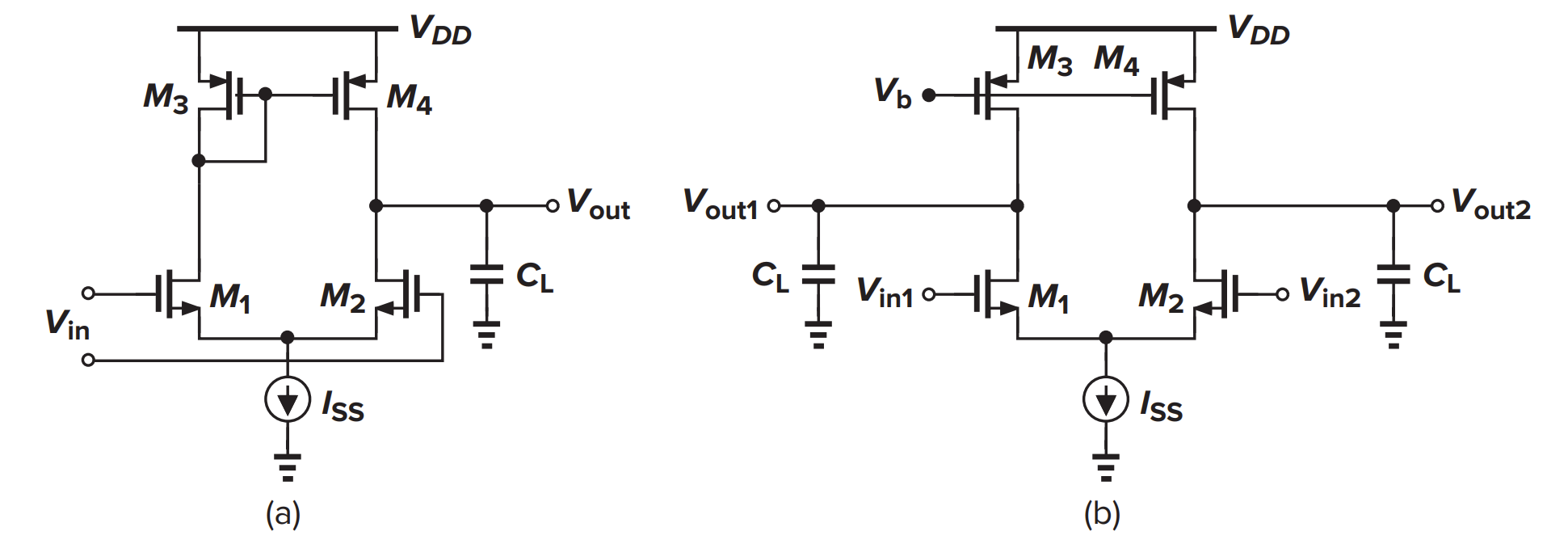
小信号增益都是

$$g_{mN}(r_{ON} || r_{OP})$$

Cascode OTA

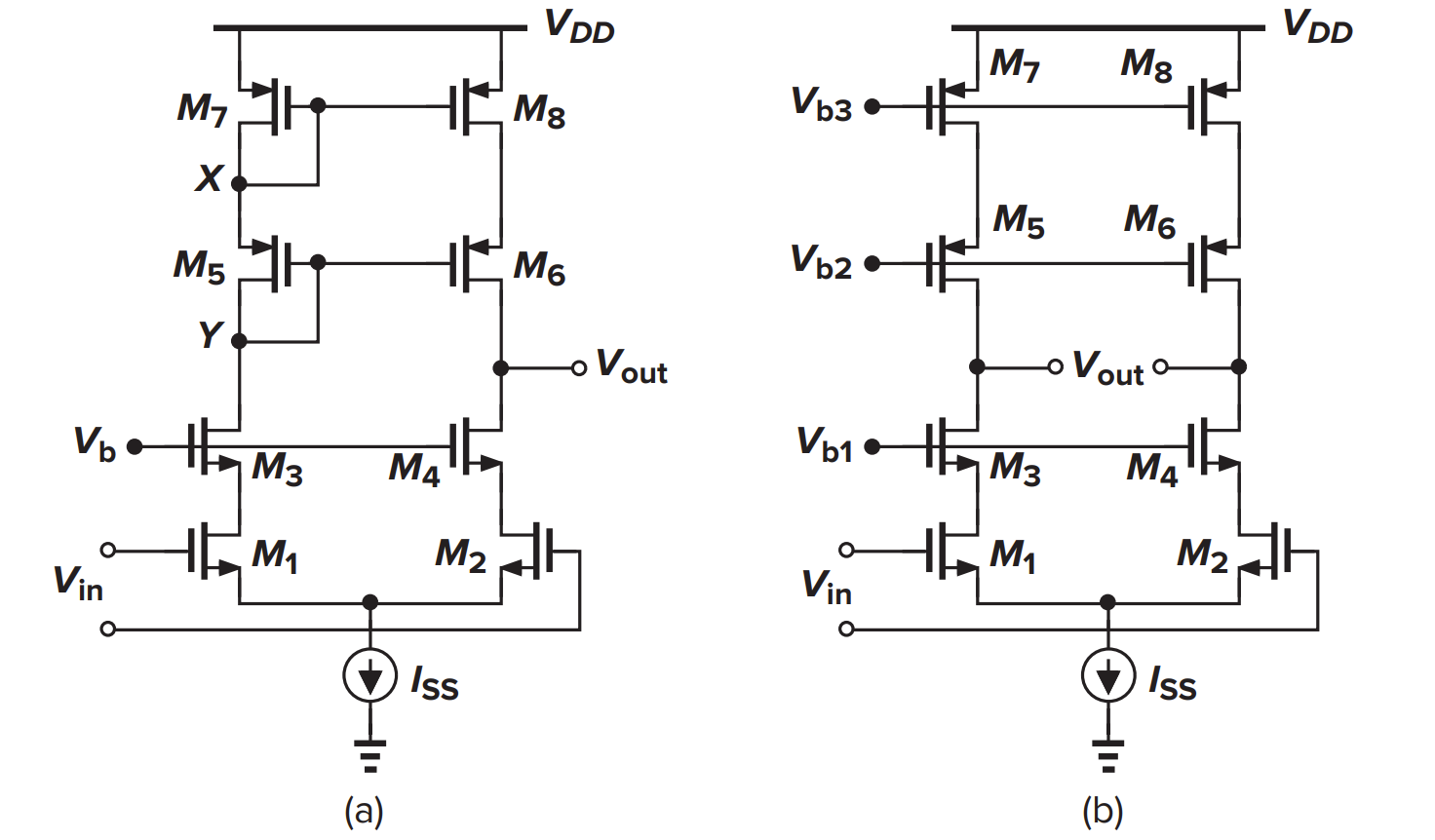
小信号增益都是

$$g_{mN}[(g_{mN}r_{ON}^2) || (g_{mP}r_{OP}^2)]$$

Power supply rejection

电源抑制比 (PSRR) 的定义是从输入到输出的增益除以从电源到输出的增益。

对于上图(a)，电源到输出的增益为1，PSRR就是小信号增益。

Slew rate*

• 当输入阶跃较大时，由于输出驱动能力/电流有限，输出可能会呈现斜率恒定的线性斜坡。这就是所谓的“回转”，输出上升/下降斜率受到最大输出驱动电流的限制。 $$SR=\frac{\mathrm{d}V_{out}}{\mathrm{d}t}=\frac{I_{SS}}{C_{L}}$$
• 当输出电压逐渐增大，反馈侧的MOS从截止到开始工作，输入又可以看成小信号，输出电压增长回归为 RC 充电的指数形式。

Basic OTA 电压范围分析

• Common-mode (CM) input range $$V_{1}=V_{t h 1}+V_{d s a t 1}+V_{d s a t_{-} S S} \leq V_{C M, I N} \leq V_{2}=V_{t h 1}+V_{D D}-V_{G S 3}$$
• Output swing $$\begin{array}{l} V_{\text {out,max }} \approx V_{D D}-V_{\text {dsat4 }} \\ V_{\text {out,min }} \approx V_{\text {dsat } 2}+V_{\text {dsat_SS }} \\ \end{array}$$ Vout 是一个高直流阻抗节点，因此其直流偏置电压对 PVT 变化非常敏感，通常需要一个负反馈回路来定义 Vout,DC，通常等于 上下限的平均值以获得最佳输出摆幅。
• Bandwidth $$\begin{array}{l} B W=\frac{1}{2 \pi\left(r_{O N} \| r_{O P}\right) C_{L}} \\ G B W=\frac{g_{m 1}}{2 \pi C_{L}} \end{array}$$ 差分对 OTA 的主要极点通常位于输出端，这里的直流电阻和负载电容相当大

Cascode OTA 电压范围分析

• Output swing is reduced by $2V_{dsat}$ $$\begin{array}{l} V_{\text {out,max }} \approx V_{D D}-\left(V_{\text {dsat } 6}+V_{\text {dsat8 }}\right) \\ V_{\text {out,min }} \approx V_{\text {dsat } 1}+V_{\text {dsat } 3}+V_{\text {dsat_ss }} \\ \end{array}$$
• Bandwidth is reduced by x100 but GBW is the same $$\begin{array}{l} B W=\frac{1}{2 \pi\left[\left(g_{m N} r_{O N}^{2}\right) \|\left(g_{m P} r_{O P}^{2}\right)\right] C_{L}} \\ G B W=\frac{g_{m 1}}{2 \pi C_{L}} \end{array}$$
• 当 Cascode OTA 用作输出缓冲的时候，范围更小了
  

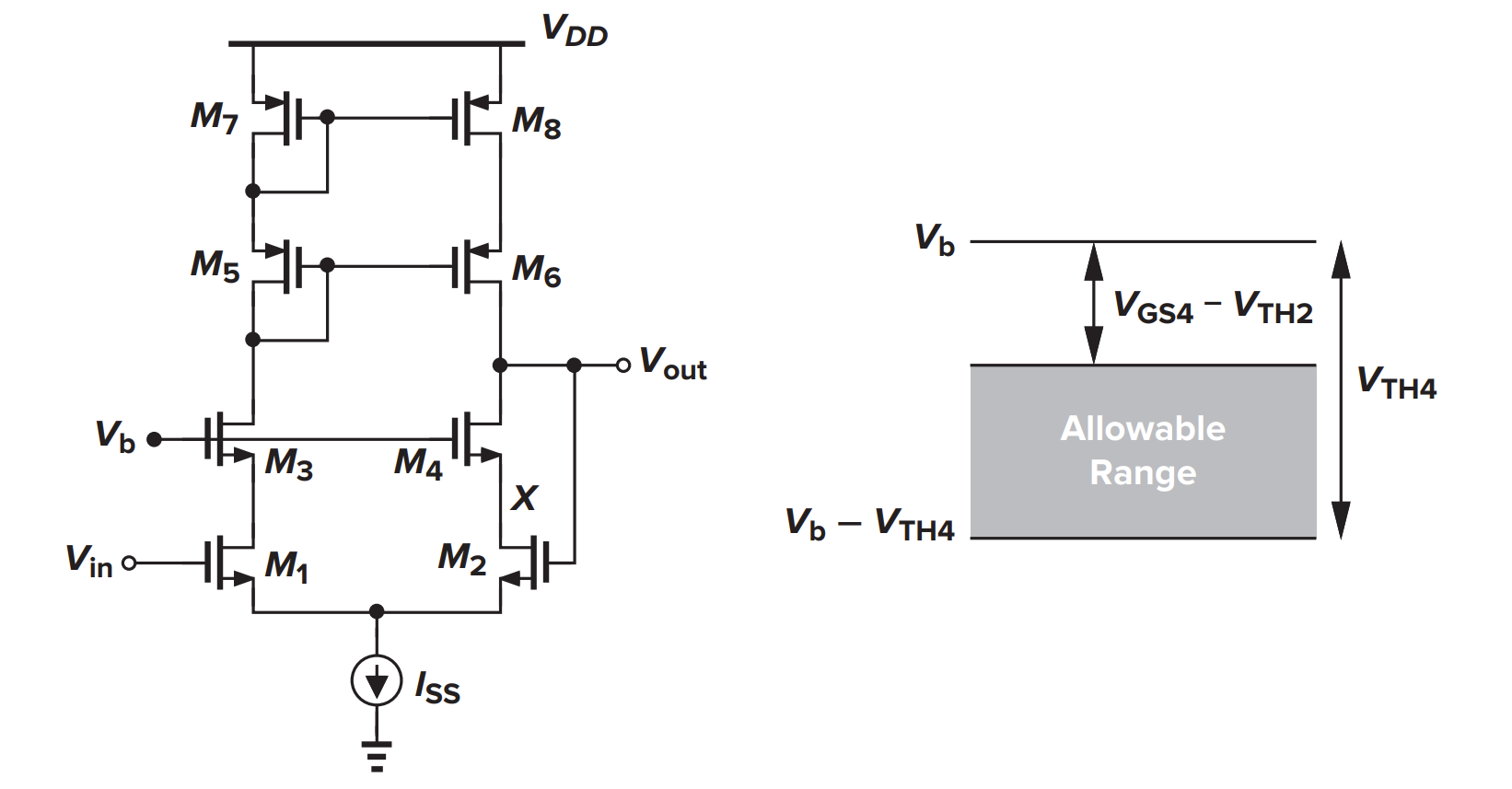
the input/output CM voltage should be equal to $V_{b} +V_{GS}4 /2$ for best output swing

Two-Stage Opamps

（Todo）

稳定性与频率补偿

负反馈的基本概念

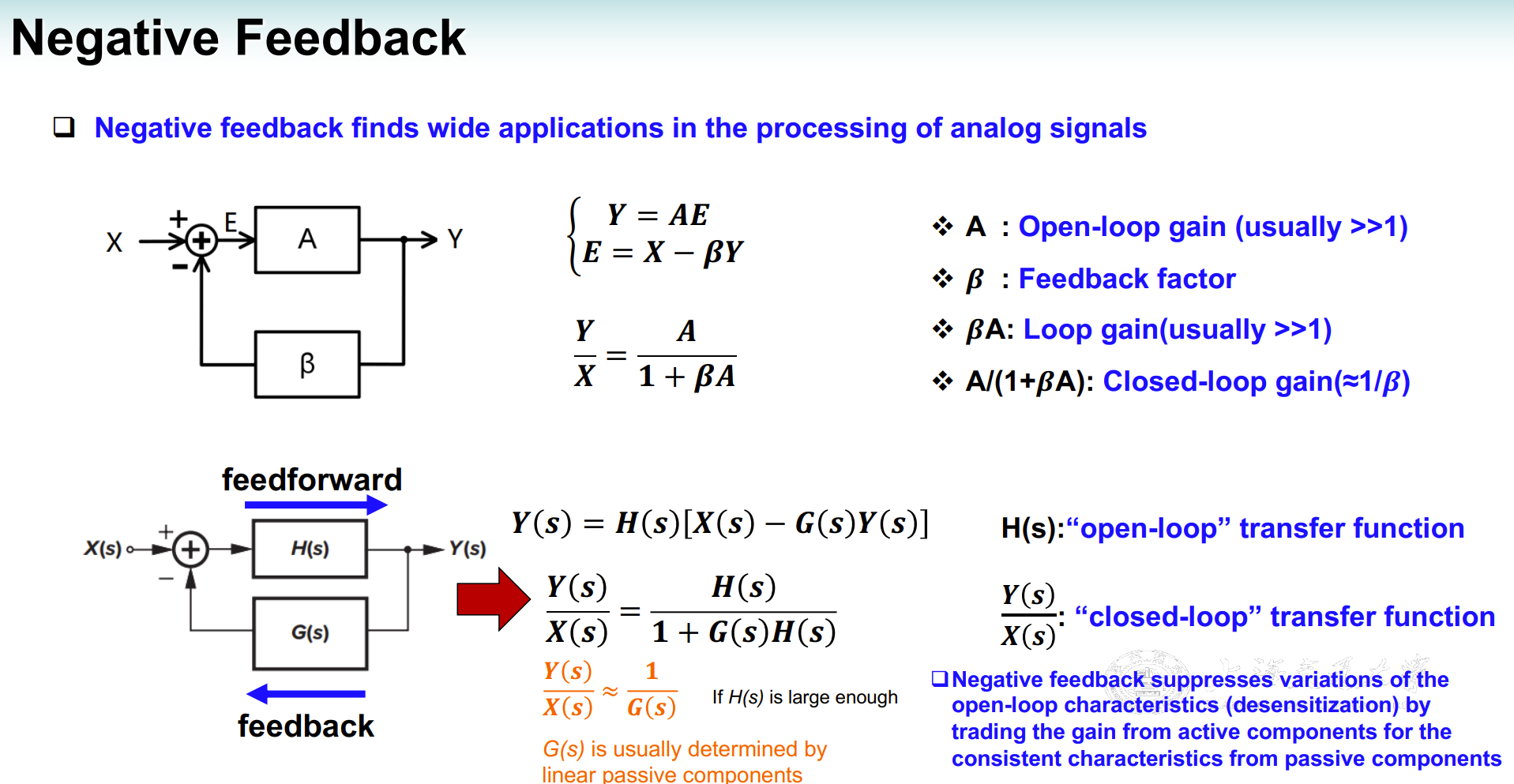
负反馈的优点

• Negative feedback provides gain “desensitization”, where the closed-loop gain is less sensitive to variations of active device parameters (PVT)
• The negative feedback extends 3-dB bandwidth by a factor of $(1+\beta A_0)$, while reducing the dc gain by the same factor and thus maintaining the same GBW
• the gain slope is more linear over a large input range

稳定性分析

环路增益在负反馈中起着核心作用，通常用于分析闭环系统的稳定性

• 若负反馈回路引入额外的180°相移（使得总相移=360°），那么负反馈变为正反馈
• 如果180°相移的时候环路增益大于1，那么会引起自激振荡

Phase Margin (PM)

相位裕度（PM）是当环路增益=1时相位和-180°之间的差，用于估计闭环系统离振荡有多近。

$$PM=\angle \beta H(\omega_1)-(-180^{\circ})$$

其中

$$|\beta H(\omega_1)|=1$$

如果相位裕度较小，闭环频率响应会在 $\omega=\omega_1$ 附近出现一个尖锐的峰值，闭环系统接近振荡。

频率补偿

将主极点向内移动，第二极点 $\omega_{p2}$ 向外移动，使得第二极点大于单位增益频率（GBW/UGB），以获得足够的相位裕度（例如 PM=60°~70°），从而提高闭环系统的稳定性。

对于两级运算放大器，有两个非常接近的主要极点

• 主要极点补偿需要一个大电容器（大硅面积），以便将主要极点移近
• 第二主要极点非常低，限制了单位增益频率，为了获得良好的 PM，要求单位增益频率小于第二主要极点频率

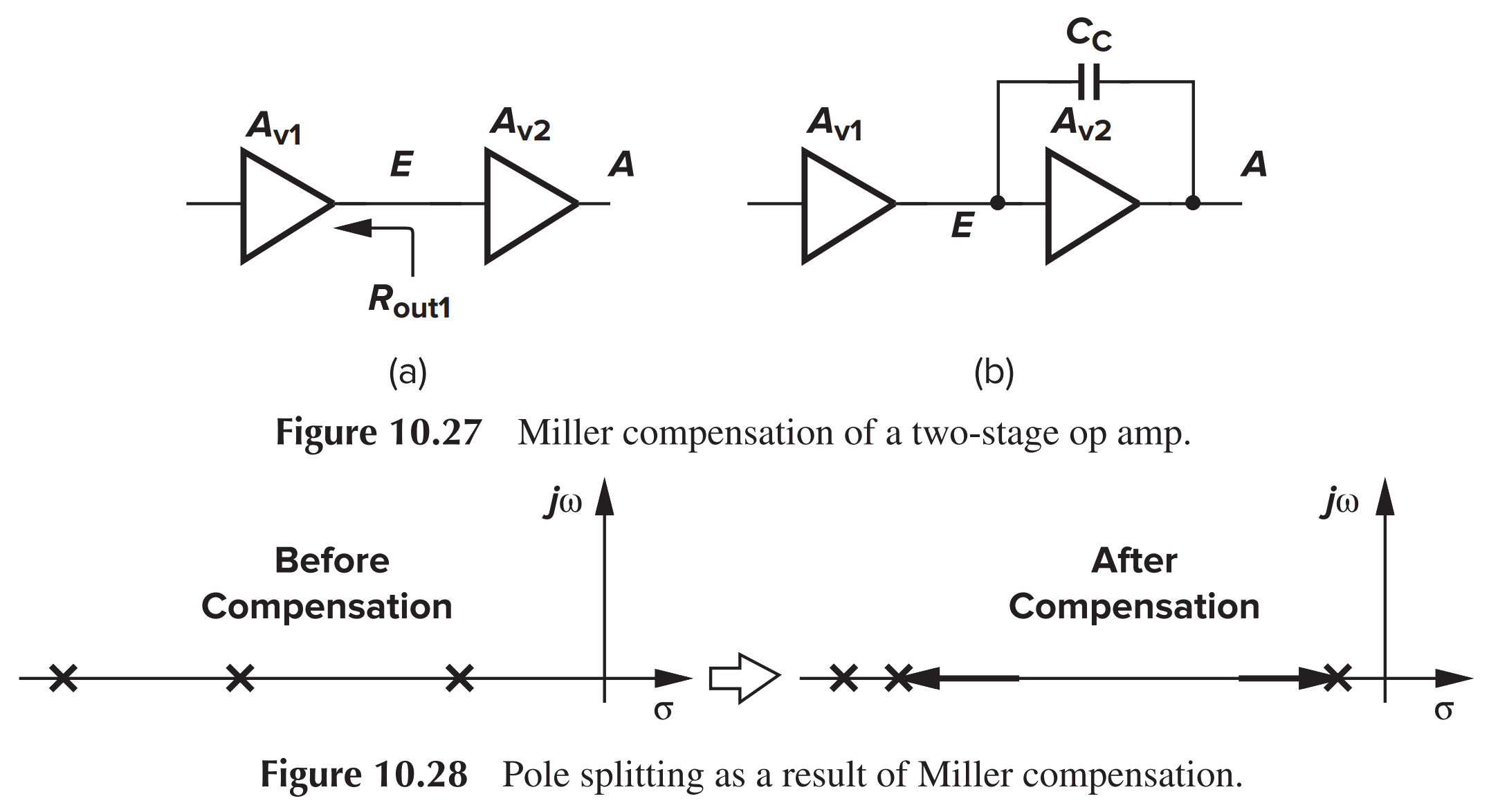
补偿方法：在第二级放大器两端接一个大电容 $C_{C}$

	补偿前	补偿后
$\omega_{p1}$	$\frac{1}{(r_{o1}//r_{o2})C_1}$	$\frac{1}{(r_{o1}//r_{o2})(1+g_{m}r_{o2})C_C}$
$\omega_{p2}$	$\frac{1}{r_{o2}C_L}$	$\frac{g_{m2}}{C_L}$

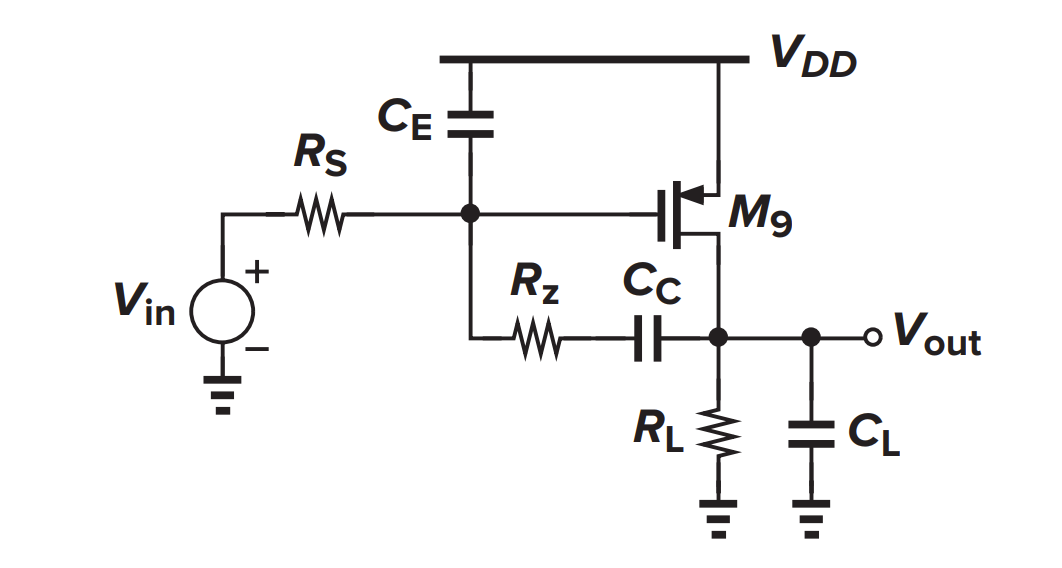
米勒补偿的零点问题

米勒补偿引入了一个右半平面零点，因为 $C_C$ 形成一个额外的前馈信号路径。

$$s_{Z}=+\frac{g_m}{C_C}$$

• RHP 零点会随频率增加增益，推高单位增益频率，从而降低 PM
• RHP 零点与 LHP 极点一样会产生负相移，进一步降低 PM

只要 $g_mR_Z>1$，在前馈路径中插入一个与 $C_C$ 串联的电阻 $R_Z$ 以改变相位，就能将零点从 RHP 移至 LHP，从而消除 RHP 零点所导致的稳定性问题。

$$s_{Z}=\frac{1}{C_C (g_m^{-1}-R_Z)}$$

噪声

基本概念

• 噪声是一个随机过程
• 瞬时振幅不可预测
• 定义噪声在每个频率的功率大小为功率谱密度（PSD），单位 $\mathrm{V}^2/\mathrm{Hz}$
• 对于白噪声，功率谱密度是常数函数
• 不相关噪声叠加，功率叠加
• 定义信噪比 $\text{SNR}= P_{\text{sig}} / P_{\text{noise}}$

电阻热噪声

• 起源：电子的随机热运动
• 零均值
• 高斯概率密度函数
• 与绝对温度成正比
• 与电流无关

$$S_v(f)=4kTR$$

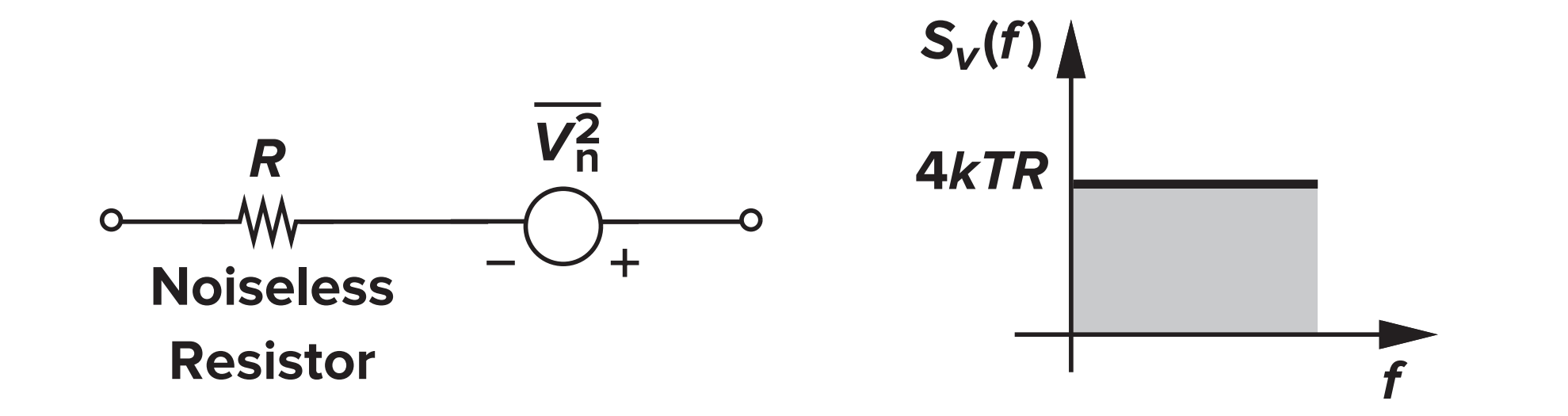
或者说

$$\overline{v^2}=4kTR$$

如果使用诺顿等效电路，

$$\overline{v^2}=4kT\frac{1}{R}$$

MOSFET 热噪声

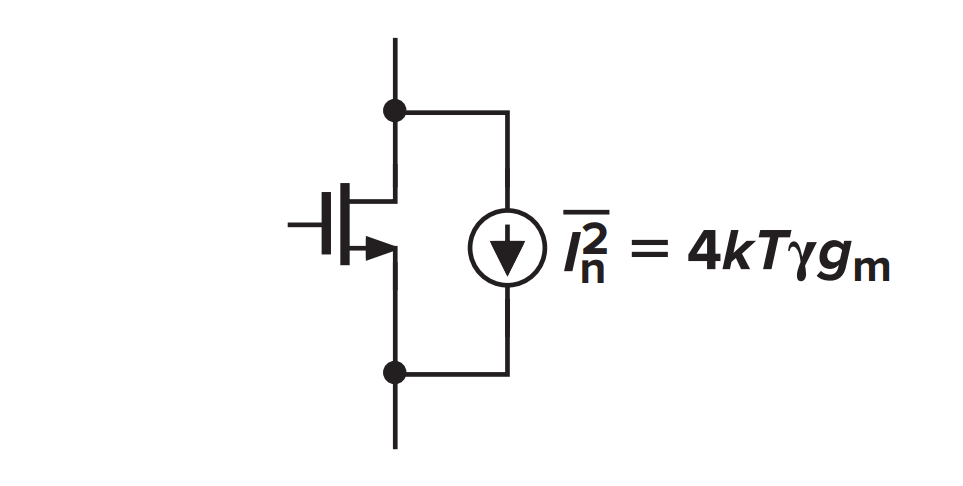
其中，γ 等于长沟道器件的 2/3，但在现代亚微米 MOS 器件中可能要大几倍。

当然，MOSFET 连接端的欧姆接触会有电阻热噪声

电容对于噪声的影响

电容不贡献噪声，但是可以像滤波器一样过滤噪声，从而限制了总噪声功率

$$\begin{aligned} S_{\text {out }}(f) & =S_{v}(f)\left|\frac{V_{\text {out }}}{V_{R}}(j \omega)\right|^{2} \\ & =4 k T R \frac{1}{4 \pi^{2} R^{2} C^{2} f^{2}+1} \\ P_{n, \text { out }}= & \int_{0}^{\infty} \frac{4 k T R}{4 \pi^{2} R^{2} C^{2} f^{2}+1} d f \\ P_{n, \text { out }}= & \left.\frac{2 k T}{\pi C} \tan ^{-1} u\right|_{u=0} ^{u=\infty} \\ & =\frac{k T}{C} \end{aligned}$$

闪烁噪声（1/f 噪声）

• 起源：与污染和晶体缺陷有关的陷阱，电荷的“陷阱”和“释放”产生了“闪烁噪声”
• 不仅存在于有源器件中，也存在于一些分立的无源元件（如碳电阻器）中
• 在低频时非常明显（因此被称为 1/f 噪声）
• 只存在于直流电中
• 取决于电流流向

$$\overline{V_n^2}=\frac{K}{C_{ox}WL}\cdot \frac{1}{f}$$

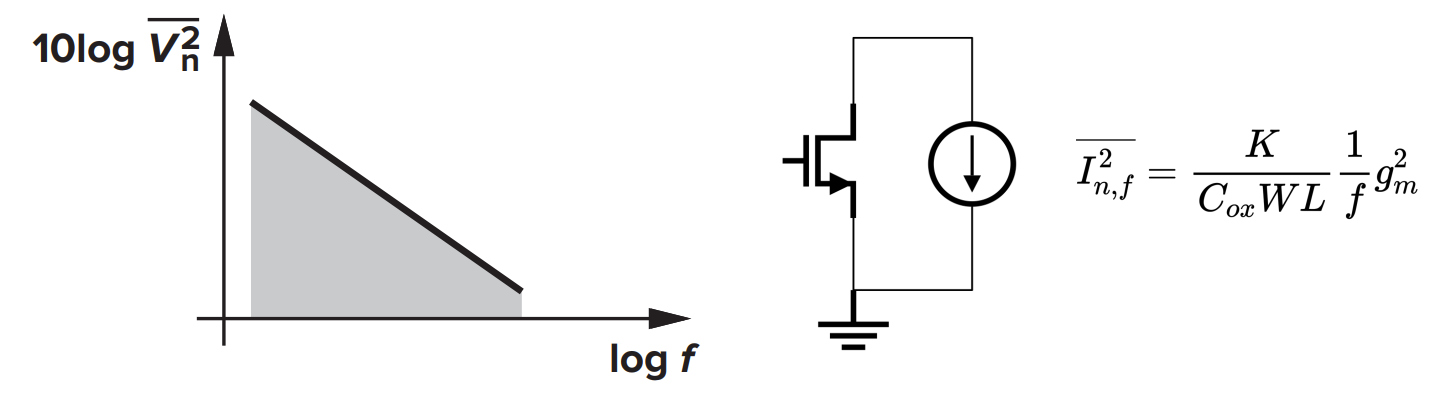
• 其中 K 与器件参数无关
• Reducing gm to improve 1/f noise (e.g., using degeneration)
• PMOS shows smaller flicker noise than NMOS

Where Thermal voltage of channel meets the flicker noise

$$f_{C}=\frac{K}{\gamma C_{o x} W L} g_{m} \frac{1}{4 k T}$$

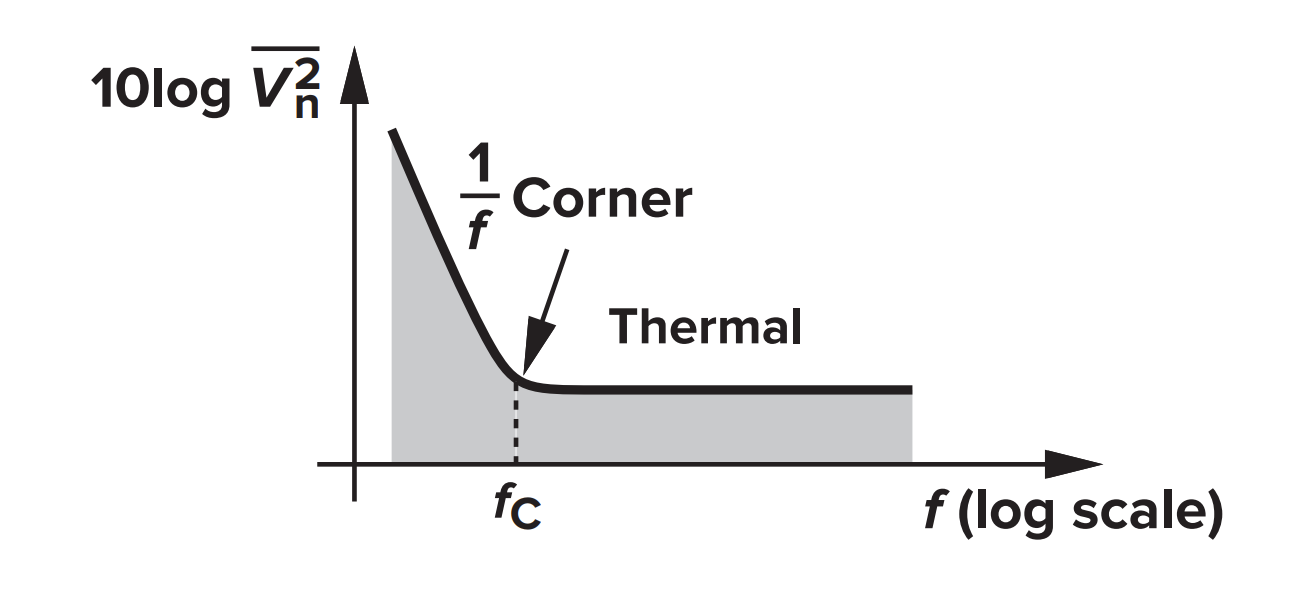
计算

CS with resistive load

$$\begin{array}{c} \overline{V_{n, \text { out }}^{2}}=\left(4 k T \gamma g_{m}+\frac{K}{C_{\text {ox }} W L} \cdot \frac{1}{f} \cdot g_{m}^{2}+\frac{4 k T}{R_{D}}\right) R_{D}^{2} \\ \overline{V_{n, \text { in }}^{2}}=\frac{\overline{V_{n, \text { out }}^{2}}}{A_{v}^{2}}=4 k T \frac{\gamma}{g_{m}}+\frac{K}{C_{\text {ox }} W L} \cdot \frac{1}{f}+\frac{4 k T}{g_{m}^{2} R_{D}} \\ \end{array}$$

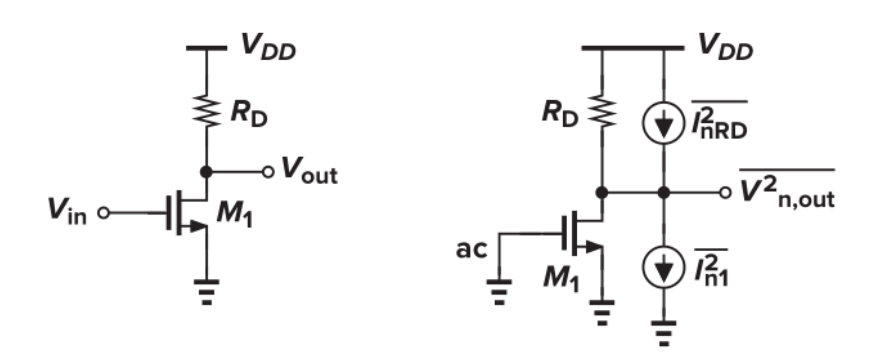
CS with current source loads

$$\begin{aligned} \overline{V_{n, \text { in }}^{2}}&=4 k T\left(\gamma g_{m 1}+\gamma g_{m 2}\right) \frac{1}{g_{m 1}^{2}} \\ &=4 k T \gamma\left(\frac{1}{g_{m 1}}+\frac{g_{m 2}}{g_{m 1}^{2}}\right) \\ \end{aligned}$$

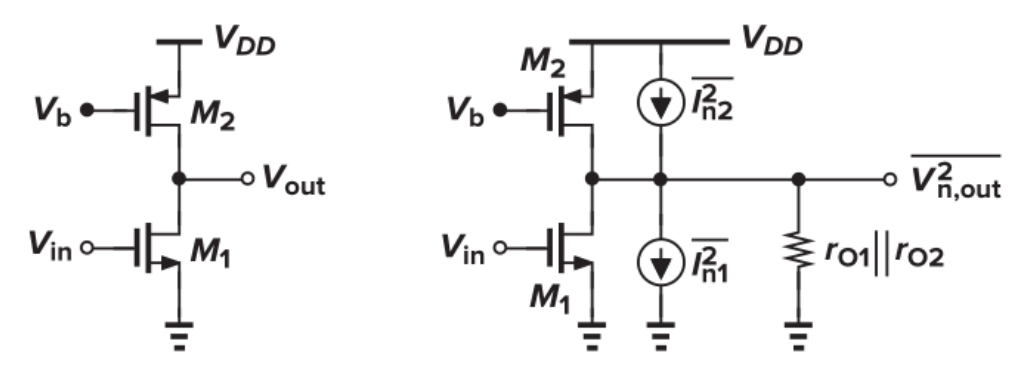
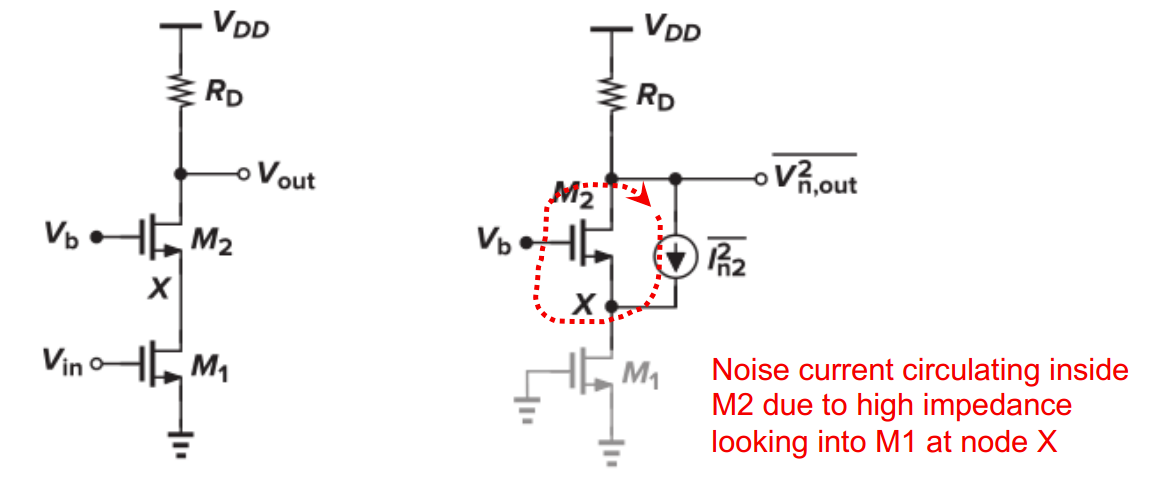
CS with cascode

$$\left.\overline{V_{n, i n}^{2}}\right|_{M 1, R D}=4 k T\left(\frac{\gamma}{g_{m 1}}+\frac{1}{g_{m 1}^{2} R_{D}}\right)$$